Система массового обслуживания E2/M/1 с обычными и сдвинутыми входными распределениями

Статья посвящена исследованию систем массового обслуживания (СМО) E2/M/1 с эрлангов-ским входным распределением 2-го порядка и с запаздыванием во времени. Первая система относятся к типу G/M/1, а вторая G/G/1. В теории СМО исследования систем G/G/1 и G/M/1 актуальны в связи с тем, что до сих пор не существует решения в конечном виде для общего случая.

В работе авторов [1] впервые приведены результаты для системы M/M/1 с запаздыванием во времени и сдвинутыми экспоненциальными входными распределениями. Показано, что среднее время ожидания требования в очереди в системе M/M/1 с запаздыванием во времени меньше, чем в классической системе M/M/1 при одинаковом коэффициенте загрузки за счет того, что коэффициенты вариации времен поступления и обслуживания становятся меньше единицы при параметре запаздывания .

Результаты [1] совместно с классикой теории СМО [2] позволяют распространить метод спектрального разложения решения интегрального уравнения Линдли (ИУЛ) также на сдвинутое эр-ланговское распределение.

Метод спектрального разложения решения ИУЛ составляет важную часть теории систем G/G/1. Для записи ИУЛ введем следующие обозначения: – функция распределения вероятностей (ФРВ) времени ожидания требования в очереди; – ФРВ случайной величины – случайное время обслуживания требования; – случайный интервал времени между поступлениями требований. Тогда нужная нам форма уравнения Линдли будет выглядеть как

^(у) =

J W (у —u^dC^u),

О, у>0;

у < О.

При изложении метода решения ИУЛ будем придерживаться подхода и символики [2]. Для этого через Л» И 64$) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно. Суть решения ИУЛ методом спектрального разложения состоит в нахождении для выражения Л *(-s)-S*(s)-l представления в виде произведения двух множителей, которое давало бы рациональную функцию от s . Следовательно, для нахождения закона распределения времени ожидания необходимо следующее спектральное разложение

дено, поэтому это решение находим классическим методом спектрального разложения решения ИУЛ аналогично [4]. Такой подход позволяет определить не только среднее время ожидания, но и моменты высших порядков времени ожидания.

Тогда, учитывая определение джиттера в телекоммуникациях как разброс времени ожидания от его среднего значения [5], получим возможность определения джиттера через дисперсию. Преобразования Лапласа функций (3) и (4) будут соответственно

Л *(-5)-5*(5)-1 = v+^Vv-^)»

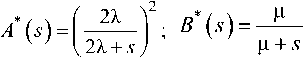
где V+(s) и V-M – некоторые рациональные функции от s, которые можно разложить на множители. Функции V+fc) и y_(s) должны удовлетворять следующим условиям [2.

• 1.    Для Re(5)>0 функция V₊W является аналитической без нулей в этой полуплоскости;

• 2.    Для Re(s)D – некоторая положительная константа, определяемая из условия

Для применения метода спектрального разложения воспользуемся результатами [2] для систем общего вида G/М/1, к которым принадлежит система E2/M/1. Выражение для спектрального разложения решения ИУЛ для системы G/М/1 задается в виде

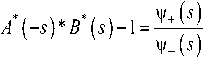
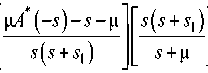
- (5)

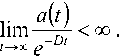
Кроме того, функции V+W и y_(s) должны

обладать следующими свойствами:

r v+(^

|s|—>со,Ке(л)>0    5

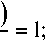
где 5 = — 51 – единственный отрицательный корень уравнения s + pi-pL4*(-s) = 0.

Выражение в первых скобках (5) не имеет ни полюсов, ни нулей в области Re(s) < 0 кроме 5 = 0и 5 = —5]. [2]. Поэтому, учитывая условия (1) и (2), за функцию V+(5) примем выражение во вторых скобках, так как его нули 5 = 0, 5 = -5]. и полюс 5 = -Ц лежат в области Re(s) < 0, а за функцию V-(^) – выражение в первых скобках:

l^p^Ref .?)<£)   5

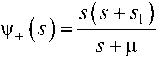
Y_(5)

—5(5 + 5) )

5 + Ц - цЛ* (-5 )

Построенные функции V+(s) и y_(s)

должны удовлетворять условиям (1)-(2).

Для окончательного построения функции

Y-(5) подставим в ее выражение

Система E2/М/1 и вывод решения для среднего времени ожидания

Для системы E2/М/1 законы распределения интервалов входного потока и времени обслуживания задаются функциями плотности вида:

alt) = 4X-te"^2Xt;                  (3)

b(t) = pie ^gZ.                     (4)

При таком задании функций (3) решения для среднего времени ожидания для системы E2/М/1 в классике по теории СМО [2-3] авторами не най-

-s(5 + 5j s + pi-pix[4X2/(2^-s)2]

-(5+ 5, )(2z.-5)"    (2X-s)‘

(s + S₁)(s-5₂)       5 — 5₂

так как квадратное уравнение

5" + (pi - 4X)5 + 4X(X - pi) = 0, полученное из знаменателя, имеет один отрицательный корень:

-s, = -(pi - 4X) / 2 - ^[(ц-4Х)/2]2 +4X(pi-X)

и один положительный корень:

^ = 1/5]-1/ц,

s₂ = (4X- ц)/2 + ^Дц^ЦТ^Т^Цц^Х) .

где 5] = (ц - 4X) / 2 + 7[(ц-4Х)/2]²+4Х(ц-Х) , аб-

В случае стабильной системы при Х<ц выполняется условие 4к(ц-^) >0.

Теперь выполнение условия (1) для построенных функций V+(s) и V-M очевидно. Это подтверждает и рисунок 1, где отображены нули и полюса отношения Y₊(s)/y_(s) на комплексной s -плоскости для исключения ошибок построения спектрального разложения. На рисунке 1 полюсы отмечены крестиками, а нули – кружками.

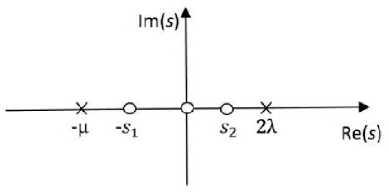
Рисунок 1. Нули и полюсы функции Y+(s)/y_(s) для системы E2/M/1

Проверка выполнения условий (2) дает hm = 1, lim '    7 = lim          = -1,

|s|-Ko S |sp® S |Л'НСС s(s —2)

следовательно, эти условия также выполнены.

Далее по методике спектрального разложения найдем константу K :

V+(s)   .. 5 + 51   ^

К = hm--— = hm---^L = —.

|s|->0 5       |s|—>0 s + p, Ц

Далее построим функцию Ф₊ (s) = К / \|/₊ (5): ^si(^s + h)

°A5)--7vTTTv Отсюда преобразование Лап-^(5 + 5|)

ласа функции плотности времени ожидания

W 5=5*Ф, 5

}         ' ^s + sj

Для нахождения среднего времени ожидания найдем производную от функции W (s) со знаком минус в точке s = 0:

^*(5) ds

5]n(s + s])-s] (s + ц)ц И (5 + 5J

S^2 -5[2Ц   11

2 2    —'

h 5,       5!Ц

В окончательном виде среднее время ожидания для системы E2/M/1 равно солютное значение корня -s, .

Система E2/М/1 с запаздыванием

Рассмотрим СМО, для которой законы распределения входного потока и времени обслуживания заданы функциями плотности как

a(t) = 4X² (/-?_o)e“^2X(Mo);         (7)

6(f) = це ^' z°).                 (8)

Такую систему мы уже обозначили E'2/M71.

Утверждение. Спектральное разложение решения ИУЛ для системы Е₂/М"/1 A* (-5) * B* (5) -1 = \|/₊ (s) / \|/_ (5) имеет точно такой же вид, что и для системы E₂/М/1.

Доказательство. Преобразование Лапласа функции (7) есть

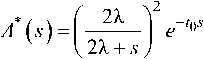
а функции (8):

5*(5)=E e-^.

Ц + 5

Из предыдущего раздела следует, что для системы E2/М/1 спектральное разложение имеет вид

V+CO ^ 5(5 + 5!)(5-5₂)

Y-(s)   (2X-s)2(5 + |i)

Для системы E2/M“/l имеем

/(-5)xB*(5)-l=        e°^s x^-e’^-1 =

V 7     7 UX-5J ц + s

= --- x—--L

\2X — s ) (i — s

Здесь показатели степени у экспонент обнуляются, и тем самым операция сдвига в спектральном разложении нивелируется. Спектральные разложения решения ИУЛ, а также преобразование Лапласа функции плотности времени ожидания (5) для обеих систем E2/М/1 и E2/M"/l совпадают, что и требовалось доказать.

Далее нам необходимо определить числовые характеристики распределений e₂ (7) и M (8). Они нужны в свою очередь для определения неизвестных параметров распределений (7) и (8) по известному методу моментов.

Определение числовых характеристикраспределения Е"2 и М"

Для их определения воспользуемся свойством преобразования Лапласа функции плотности воспроизводить моменты:

ds

d / 2Х У ds V^X+s)

8Х² -t_nS

------Ге

(2X + s)

Л 2Х Л ^to'

— 1 / X + Zq .

|.s=0

Отсюда среднее значение интервала между поступлениями требований: T^ - X ' + /„. Найдя вторую производную от преобразования Лапласа функции (7) при s = 0, определим второй началь- ный момент интервала между поступлениями

=TTT + 2T‘ + ?0- Тогда коэффициент ds2 n 2X2 X u вариации cx =1/ V2(l + X/0).

Второй начальный момент интервала между d2A*(s)

поступлениями ds²

—^= + 2 —+ /g, 2X² X ⁰ от-

куда m 2 "*" ^ + ^o ' Отсюда коэффициент 2X~ X вариации

cx =1 / V2(l + Xf0)

Поступив аналогично для распределения M с преобразованием Лапласа функции (8), получим среднее значение времени обслуживания Ч = p-1 + /0 , а коэффициент вариации сц = 1 / (1 + pZ0). (10)

Заметим, что для распределения Е₂: 4=V,c_x=l/^. Сравнивая результаты числовых характеристик ^Tv 7 для распределений Е₂ и E2 , можно увидеть разницу между ними, полученную ввиду сдвига законов распределений на ^fo > 0- Коэффициент вариации для распределения ^2' ^Ck уменьшается при сдвиге в O+MJ раз по сравнению с коэффициентом ^X для распределения Е₂.

Для времени обслуживания по закону M коэффициент вариации c^ уменьшается при сдвиге в (l + ^o) раз по сравнению с коэффициентом c . для распределения M.

Учитывая, что среднее время ожидания в системе G/G/1 связано с коэффициентами вариаций времени между поступлениями требований и времени обслуживания квадратичной зависимостью, в системе с запаздыванием вре- мя ожидания будет меньше, чем в обычной си- стеме.

Теперь, исходя из полученных параметров распределения для системы e₂/m-/1 , время ожидания для нее определяем из выражения (6), где параметры х^/сч-у^р^/ (ч - ч), ^ = (p - 4X) / 2 + V[(p-4X)/2]² +4X(p-X).

Теперь, задав в качестве входных параметров для расчета системы e₂/m71 полученные выше значения 4.' Д | ’ ^CX ’ ^c u ’ ^0 ’ можно рассчитать среднее время ожидания по выражению (6) для диапазонов изменения коэффициентов вариаций c_x e(o,l/V2) и с_ц e(O,l), определяемыми выражениями (9) и (10) соответственно в зависимости от величины параметра сдвига ч >0.

Ниже в таблице 1 приведены данные расчетов для системы E2/MV1, полученные при малой 4 = 0,1), средней (/^ = 0,5) и высокой нагрузки (/2 = 0,9) и параметре сдвига Ч =0,01; 0,1; 0,5; 0,9-Для сравнения в правой колонке приведены данные для обычной системы E2/М/1.

Таблица 1. Результаты экспериментов для СМО

Ег/М'/! иЕ₂/М/1

Входные параметры				Среднее время ожидания
Р	сх	СЦ	Ч	Для е-/е;/1	Для е2/е2/ 1
0,1	0,64	0,1	0,9	0,000	0.030
	0,67	0,5	0,5	0,005
	0,70	0,9	0,1	0,023
	0,71	0,99	0,01	0,029
0,5	0,39	0,1	0,9	0,003	0,618
	0,53	0,5	0,5	0,132
	0,67	0,9	од	0,491
	0,70	0,99	0,01	0,605
0,9	0,13	0,1	0,9	0,055	6,588
	0,39	0,5	0,5	1,609
	0,64	0,9	0,1	5,322
	0,70	0,99	0,01	6,456

С уменьшением значения параметра ^0 среднее время ожидания в системе Еэ/М71 стремится к среднему времени ожидания в системе E2/М/1. Данные таблицы 1 подтверждают тот факт, что за счет уменьшения коэффициентов вариации сх и Сц из-за ввода параметра сдвига t^ уменьшается среднее время ожидания в системе.

Заключение

Полученные результаты приводят к следующим выводам.

• 1.    Операция сдвига во времени, с одной стороны, приводит к увеличению загрузки системы с запаздыванием. Для системы e;/M’/i с запаздыванием загрузка увеличивается в (1 + X/q)/ (1 + ц?₀) раз по сравнению с обычной системой E₂/М/1.

• 2.    Операция сдвига во времени, с другой стороны, уменьшает коэффициенты вариаций интервала между поступлениями и времени обслуживания требований. В связи с тем, что среднее время ожидания в системе G/G/1 связано с коэффициентами вариаций интервалов поступления и обслуживания квадратичной зависимостью, среднее время ожидания в системе с запаздыванием будет меньше, чем в обычной системе при одинаковом коэффициенте загрузки. Например, для системы e;/m^_/i при загрузке p=0,9 и параметре сдвига C^ уменьшается с 1 для обычной системы до 0,13; коэффициент вариации времени обслуживания ^сц уменьшается с 1/V2 до 0,1, а время ожидания уменьшается с 6,59 единиц времени для обычной системы до 0,055 единиц времени.

• 3.    Изложенные результаты справедливы только для одинаковых параметров сдвига t ₀ для распределения интервалов между поступлениями требований и времени обслуживания.