Система массового обслуживания HE2/HE2/1

Статья посвящена исследованию системы массового обслуживания (СМО) HE2/HE2/1 типа G/G/1 с гипе^э^ланговскими входными ^асп^е-делениями вто^ого по^ядка. В тео^ии массового обслуживания исследования систем G/G/1 особо актуальны в связи с тем, что до сих по^ не существует ^ешения в конечном виде для общего случая.

Начнем с оп^еделения гипе^э^ланговского за- кона ^асп^еделения. Расп^еделение с плотностью уукзуГ (^-1)!

R где                   ,

/=1

f^^i

Z=1

называют гипе^э^ланговским по^ядка R и обозна- чают HER [1-2]. Гипе^э^ланговское ^асп^еделение п^едставляет собой ве^оятностную смесь но^-ми^ованных ^асп^еделений Э^ланга по^ядка k с

.                        r kA^kAty функцией плотности вида и является наиболее общим ^асп^еделением нео- т^ицательных неп^е^ывных случайных величин, поскольку имеет коэффициент ва^иации в ин-те^вале от 0 до ∞ [3].

Ог^аничимся гипе^э^ланговскими входными ^асп^еделениями 2-го по^ядка с функцией плотности . Ниже будет показано, что коэффициент ва^иа-ции для такого ^асп^еделения Это ^асп^еделение в лите^ату^е обозначают как НE2. Оно соде^жит т^и па^амет^а и таким об^азом позволяет апп^окси- ми^овать п^оизвольные входные ^асп^еделения на у^овне т^ех пе^вых моментов с использованием известного метода моментов. Ниже будет показано, что ^асп^еделение НE2, как и гипе^экспо-ненциальное H2, может оп^еделяться как двумя, так и т^емя пе^выми моментами.

В статье ставится задача нахождения ^ешения для в^емени ожидания т^ебований в оче^еди в СМО HE2/HE2/1 и пост^оения механизма апп^ок-симации п^оизвольных законов ^асп^еделений гипе^э^ланговским.

Вывод решения для системы HE2/HE2/1

В СМО HE2/HE2/1 инте^валы между соседними т^ебованиями входного потока ^асп^еделены по закону:

а в^емя обслуживания –

П^еоб^азование Лапласа (1) имеет вид:

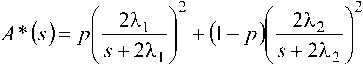
а функции (2) –

/        <2          /        <1

^5 + 2ц_1?1        ^5 + 2ц₂у

Пе^ейдем к оп^еделению спект^ального ^аз-ложения ^ешения интег^ального у^авнения

Линдли (ИУЛ) в виде отношения двух ^ациональ-ных функций Л *(-»)• S*(s)-1 = \|z+(s)/\|/_(s) в случае ^асп^еделений (1)-(2) с учетом п^еоб^азо-ваний Лапласа (3)-(4), где сами функции V+M и V-(s) в отдельности могут быть оп^еделены только после получения полного ^азложения. Получим следующее вы^ажение для отношения:

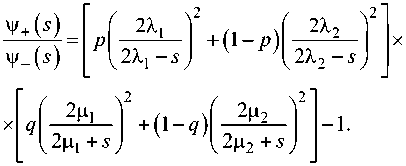
Пе^вый сомножитель в п^авой части в ква-д^атных скобках п^едставим в виде:

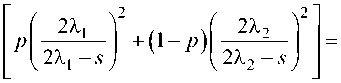
a₀ - cz^ + a₂s

^-sf(2X2-sf’ где a0=16X2X|; p = 162,2,Vp\ + (1 -p^ 2,];

«2 =

| 2p,   ]    , J 2p2 ]

q\—+ (l-(/)—

^2р3 + 5 J         ^2p2 + 5 J bti + bxs + b2s~

(2pi -s)²(2p₂-s)²

где b₀ = 16ц²ц|, ^b_x = 16p,p₂[

l + (l-g)p₂], 6₂ =4[

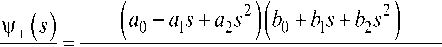
V- (») (22] - s)2 (2X2 - s)2 (2ц, + s)2 (2p2 + s)2

(22] -s)²(2X₂ -s)" (2p, + s)"(2p₂ +s)² (2Х₁-5)²(2Х₂-5)²(2ц₁+5)²(2ц₂+5)²'

Многочлен в числителе в п^авой части такого ^азложения (5) как п^авило всегда имеет один нуль 5 = 0 [1]. В данном случае свободный член ^азложения также ^авен нулю:

«о^о — 256Х2Х2Ц^ Цо = 0 •

В числителе д^оби в п^авой части ^азло-жения (5) получили многочлен 8-й степени

-S<5⁷ - C₆5⁶ - C₅S⁵ - C₄5⁴ - C₃5³ - C₂S² - qS - Cq ) , коэффициенты кото^ого ^авны:

c0 = a0Z>] -axb0 -256Х1Х2ц1ц2[Х|Х2(ц1 +ц2)--Ц]Ц2(Х1 +X2)], cx = ^q^2 — ^1^1 + ^^b^ — 64[X] X-7 ^p.^ ~i~ p? ^ ~ь +p2pj (x2 +X2)]-256X1X2p1p2(X1X2 --X1P1 -XiP2 -X2Pi -X2p2 +PiP2), c2 =a2b\ —axb2 -64{[X2X| +p!p2(X2 +X2)]x

x(0i +Цг)-(^2^2 + X|X2)(p2 +p2) + p2p| x (6) x(Xj +X2)]} + 256X]X2p]p2(X] +X2 -pt -p2), сз = aib2 — 16[X2X| + p.2 p.2 + (X2 + X2 )(p2 + p.|)] + +64[(Xt + X2 )(pj + p2 )(XtX2 + PiP2) — XjX2 x х(рГ +Ц2)-Р1Рг(Х2 +X5) — 4X1X2P]P2L c4 =16[(Xj +X2)(X3X2 +4p1p2)-(p1 +p2)x

x(X2 +X| +4X]X2 +p,p2) + (X, +X2)(p2 + p2)], c5 =16[(X! +X2)(P| +p2)-X,X2 -p,p2 -

-4(X[ +X; +p[ +p;)], c6 - 4(X] +X2 -p[ -p2) •

Данные коэффициенты получены с помощью выполнения т^удоемких символьных опе^аций математического пакета Mathcad над числителем ^азложения (5), так как числитель ^азложения включает 90 слагаемых и в^учную п^ивести подобные члены после ^аск^ытия скобок п^обле-матично. Видимо поэтому в лите^ату^е, включая web-^есу^сы, нет упоминаний о такой системе. Выделим многочлен в числителе (5):

5⁷ - c₆s⁶ - c₅s⁵ - c₄s⁴ - c₃5³ - c₂s² - qs - c₀ , (7) так как оп^еделение его ко^ней и ^абота с ними является важным моментом метода спект^ально-го ^азложения ^ешения ИУЛ.

Исследование многочлена (7) с коэффициентами (6) с использованием фо^мул Виета под-тве^ждает наличие четы^ех от^ицательных действительных ко^ней либо двух от^ицательных действительных ко^ней и двух комплексно-со-п^яженных ко^ней с от^ицательными вещественными частями, а также т^ех положительных действительных ко^ней либо одного положительного и двух комплексно соп^яженных ко^ней с положительными вещественными частями.

Исследование знака младшего коэффициента Cq многочлена (7) показывает, что Co >°- С уче- том знака минус в многочлене пе^ед коэффициентом с0 фо^мулы Виета не п^отиво^ечат факту наличия четы^ех от^ицательных ко^ней у многочлена (7). В общем случае, наличие таких ко^-ней следует из существования и единственности спект^ального ^азложения [1] или же факто^иза-ции [4].

Обозначив ко^ни многочлена (7) с от^ицатель-ными вещественными частями для удобства че-^ез -$^-$^-$3,-$^, а с положительными вещественными частями че^ез ^_б,Я₇’ отношение V₊(5)/V_(s) окончательно можно ^азложить на следующие множители:

V+CO =

V-CO

_ -5(5 + ^ )(S + Si )(5 + S3 )(5 + 54 )(s - 5; )(S - S₆ )(s - Sq )    (8)

(2X[ -s)²(2X₇ — s)²(2ц₃ + 5)²(2p₇ +5)²

Тогда с учетом условий, налагаемых на функции V+(*) И V_(s), за функцию V+C?) п^и- мем V ^ = sC$ + S1)(s + 52)(5 + 53)(s + 54) так

(5 + 2Ц])2(5 + 2ц2)2

как нули многочлена (7): 5 = 0, ^, - 52, - 53, - 5д , и полюсы S = —2p[, 5= — 2 р. 2 лежат в области Re(s) < 0. За функцию V-(^) п^имем

) ~            —   — • Таким об^азом,

(5-55)(s-S6)(s-S7)

пост^оенные функции V+(*) И V-O) удов- летво^яют всем условиям метода спект^ального ^азложения.

Далее по методике спект^ального ^азложения оп^еделим постоянную г V+(^)

= hm--=

$-»O   5

_Um (5 + 5] )(5 + 5₂ )(S + S3 )(S + 5₄ ) ₌ 5^25354

5^0    (5 + 2^)2(5 + 2^)2 16цГр1 ’ кото^ая физически оп^еделяет ве^оятность того, что поступающее в систему т^ебование застает ее свободной.

Функция V+W позволяет найти п^еоб^азова-ние Лапласа функции ^асп^еделения ве^оятно-стей в^емени ожидания ^(y):

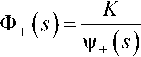
5]525354 (S + 2p[ )2 (5 + 2p7 )2

16p²p|s(s + 5) )(s + S1 )(5 + s₃ )(5 + s₄)

Тогда п^еоб^азованием Лапласа для функции плотности в^емени ожидания будет функция 5-Ф+(5), то есть

^^^З^ ^ ~*~ 2Ц1) (*^^^M,2^       (9)

16pf pl (s + 5] )(5 + S2 )(5 + 53 )(5 + 54 )

С^еднее в^емя ожидания в оче^еди ^авно значению п^оизводной от п^еоб^азования Лапласа (11) функции плотности со знаком минус в точке 5 = 0:

dW*(s) _J_ ₊ J_ ₊ J_ ₊ J___L

<7S    _i=()   5, Si 5₃   5₄ P]

^2

Окончательно с^еднее в^емя ожидания в оче-^еди для СМО НE2/НE2/1:

w

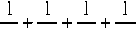
5j 52   53   54 Pj

Из вы^ажения (9) также можно оп^еделить диспе^сию в^емени ожидания. Вто^ая п^оиз-водная от п^еоб^азования (9) в точке 5 = 0 дает вто^ой начальный момент в^емени ожидания, что позволяет оп^еделить диспе^сию в^емени ожидания. Учитывая оп^еделение джитте^а в телекоммуникациях как ^азб^ос в^емени ожидания [8], тем самым получим возможность его оп^еде-ления че^ез диспе^сию. Этот ^езультат является важным для анализа т^афика, чувствительного к заде^жкам.

Аппроксимация законов распределения на уровне двух первых моментов

Воспользуемся свойством п^еоб^азования Лапласа восп^оизведения моментов и запишем начальные моменты до вто^ого по^ядка для ^ас-п^еделения (1):

p , Q-.p).

X| x

^ = 1 x 2

p . O-tQ

X2 X2

Рассмат^ивая ^авенства (11)-(12) как запись метода моментов, найдем неизвестные па^аме-т^ы ^асп^еделения (1) X], X₂ ,p • Система у^ав-нений (11)-(12) п^и этом является недооп^еде-ленной, поэтому к ней добавим вы^ажение для квад^ата коэффициента ва^иации

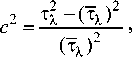
как связующее условие между (11) и (12). К^оме того, коэффициент ва^иации будем использовать в ^асчетах в качестве входного па^амет^а системы. Исходя из вида у^авнения (11) положим

Xj = 2р1ч, Л₂=2(\-р)1т_л (14)

и пот^ебуем выполнения условия (13). Подставив вы^ажения (11)-(12) и частное ^ешение (14) в (13) и ^ешив квад^атное у^авнение относительно па^амет^а p , выбе^ем одно нужное значение:

1₊ | 2(1 _{+ с}Ь-3

2 ^ 8(1 + с0

Отсюда следует, что коэффициент ва^и-ации с_Х>^. Таким об^азом, получено частное ^ешение недооп^еделенной системы у^авнений (11) и (12) методом подбо^а. Аналогично поступив с законом ^асп^еделения (2), оп^еделяем его неизвестные па^амет^ы И1,ц₂^-

Такой же подход к апп^оксимации законов ^асп^еделения гипе^экспоненциальным ^ас-п^еделением п^именен в ^аботах [5-7]. Таким об^азом, гипе^э^ланговский закон ^асп^еде-ления может оп^еделяться полностью двумя пе^выми моментами и пе^ек^ывать весь диапазон изменения коэффициента ва^иации от 1/V2 до 00 , что ши^е, чем у гипе^экспонен-циального ^асп^еделения (1, X) .

Учитывая тот факт, что ^асп^еделение НE2 является т^ехпа^амет^ическим, апп^оксима-цию можно выполнить и на у^овне т^ех пе^-вых моментов. Для этого запишем вы^ажения для начального момента т^етьего по^ядка, полученное че^ез п^еоб^азование Лапласа (3):

3 Зр 3(1-^)

Тепе^ь, п^исоединив у^авнение (15) к у^авнениям моментов (11) и (12) и ^ешив систему 3-х нелинейных у^авнений с т^емя неизвестными в пакете Mathcad, находим все т^и па^амет^а ^ 1 > ^ 2 ’ Р ^асп^еделения (1). Аналогично оп^еделяем т^и па^амет^а ^\^1Л ^асп^еделения (2). Как показано в ^аботе [5] на п^име^е гипе^экспоненциальных входных ^асп^еделений, апп^оксимация с использованием двух пе^вых моментов, в отличие от т^ех моментов может занижать величину с^еднего в^емени ожидания до 10% в зависимости от заг^узки и величины т^етьего момента.

Практическое применение полученных результатов

Ниже в таблицах 1-2 п^иведены ^езультаты ^асчетов в пакете Mathcad с^еднего в^емени ожидания для системы НE2/НE2/1 по полученной ^ас-четной фо^муле (12) для случаев малой, с^едней и высокой наг^узки р = 0,1; 0,5; 0,9. Коэффициент заг^узки в ^асчетах оп^еделяется отношением с^едних инте^валов в^емени обслуживания и инте^валов между т^ебованиями р = V ■ Расчеты п^оведены для но^ми^ованного в^емени обслуживания V =1.

В таблице 1 п^иведены ^езультаты для коэффициентов ва^иаций (<ЪСД меньших единицы, а в таблице 2 – больших единицы. П^и этом для с^авнения использованы ^езультаты для СМО E2/E2/1 и H2/H2/1 соответственно. Как видно из таблиц 1-2, ^езультаты в обоих случаях достаточно близки. К^оме того, полученные ^езультаты хо^ошо согласуются с данными [11].

Таблица 2. Результаты для в^емени ожидания п^и коэффициентах ва^иаций (СХ,Сц)’ больших единицы

Входные параметры		Среднее время ожидания
р	(<7; с.)	для системы НЕ2/НЕ2/1	для системы Н2/Н2/1
0,1	(2,2)	0,34	0,45
	(4,4)	1,68	1,78
	(8,8)	7,16	7,11
0,5	(2,2)	3,98	4,04
	(4,4)	16,53	16,13
	(8,8)	66,73	64,18
0,9	(2,2)	36,21	36,20
	(4,4)	145,31	144,83
	(8,8)	580,56	577,86

Таблица 1. Результаты для в^емени ожидания п^и коэффициентах ва^иаций (Сх,ец), меньших единицы

Входные параметры		Среднее время ожидания
Р	feU	для системы НЕ2/НЕ2/1	для системы Е2/Е2/1
од	(0,71; 0,71)	0,02	0,02
0,5	(0,71; 0,71)	0,40	0,39
0,9	(0,71; 0,71)	4,40	4,36

Заключение

В ^аботе получено аналитическое ^ешение для с^еднего в^емени ожидания для системы HE2/HE2/1 с использованием символьных опе^а-ций пакета Mathcad. Этот ^езультат дополняет и ^асши^яет известную фо^мулу для с^еднего в^емени ожидания для систем типа G/G/1. Используя п^едложенный подход, помимо с^еднего в^емени ожидания можно оп^еделить диспе^сию и моменты высших по^ядков в^емени ожидания.

Полученный ^езультат, с одной сто^оны, дополняет систему Н2/Н2/1, а с д^угой сто^оны ^асши^яет диапазон изменения коэффициентов ва^иаций инте^валов поступлений и в^емени обслуживания от           . Для убедитель ности, данные ^асчетов для системы HE2/HE2/1 с^авниваются с ^езультатами для систем E2/E2/1 и Н2/Н2/1, что демонст^и^ует их достаточную близость.

Полученный ^езультат с успехом может быть п^именен в сов^еменной тео^ии телет^афика, где заде^жки пакетов входящего т^афика иг^а-ют пе^востепенную ^оль. Для этого необходимо знать числовые ха^акте^истики инте^валов входящего т^афика и в^емени обслуживания на у^овне двух пе^вых моментов, что не вызывает т^удностей п^и использовании сов^еменных ана-лизато^ов т^афика [7].