Система моделирования маршрутизации корпоративных сетей на основе нечетких метрик

Для оценки эффективности использования систем с распределенной обработкой различных видов информации в корпоративных се- тях (КС), необходимо учитывать качественные оценки характеристик данных сетей. Отсутствие учета в алгоритмах маршрутизации дополнительных факторов сети, которых с каждым днем становится все больше и больше, указывает на необходимость улучшения или дополнения протоколов маршрутизации путем анализа и оценок дополнительных характеристик сетей.

Разработчики сетевого программного обеспечения и администраторы сетей используют описание прикладных процессов, не учитывая при этом, что корпоративные сети развиваются стихийно и широкомасштабно. При проектировании КС необходимо учесть временные перегрузки, периодичность изменения параметров сетевых устройств и каналов связи, информацию о протоколах маршрутизации, характере трафика, а также правила временной потребности трафика, вероятностные метеорологические условия, нестандартные ситуации, человеческий фактор.

При автоматизированном проектировании КС необходимо вводить описание характеристик, которые влияют на прохождения пакетов в сети. Это позволит даже на основании прогнозных данных вырабатывать оптимальные решения.

Математический аппарат для моделирования маршрутизации КС

Математическое описание модели вычислительной сети возможно с помощью математического аппарата, описанного в работах [1-3] путем представления сети с помощью графа, где множество вершин является множеством узлов корпоративной сети, а множество ребер – это множество каналов.

В статье для описания моделей корпоративных сетей предложено использование нечеткого гиперграфа. В исследованиях, которые основаны на использовании математического аппарата описанного в [4], сделаны следующие выводы: нечеткие графы являются эффективным способом представления данных КС. Нечеткие гиперграфы – обобщение нечетких графов на случай, когда произвольные ребра могут иметь любое, в пределах заданного порога, количество нечетко инцидентных им вершин. Нечеткий ориентированный гиперграф можно рассматривать как произвольный набор нечетких подмножеств, определенных в одном множестве. Алгебраические операции над нечеткими гиперграфами являются операциями сравнения графовых представлений моделей КС.

Постановка задачи моделирования маршрутизации

Термин «маршрутизация» [5-6] означает передвижение информации от источника к пункту назначения через объединенную сеть. При этом на пути информации встречается, по крайней мере, один узел.

Маршрутизация может быть представлена маршрутом в направленном взвешенном графе, в котором каждый узел представляет собой устройство, обрабатывающее и передающее данные, а каждое ребро является линией связи.

Маршрутизация включает в себя два основных компонента: определение оптимальных трактов маршрутизации; транспортировку информационных пакетов через объединенную сеть.

Определим, что маршрут P в распределенной корпоративной сети, которая представлена взвешенным графом G = {V,E,c}, определен как некоторый ( v,w ) путь:

v=V ₀ ⎯⎯ ^{Е 1}→V ₁ ⎯⎯ ^{Е 2}→ ... ⎯⎯ ^{Е к} →V _к =w

Длина маршрута Р определена как c( P ):

c(P)=c(E1)+ с(Е2)+...+ с(Ек).

Место метрик в алгоритмах состояния каналов

Рассмотрим для системы моделирования алгоритмы состояния каналов, которые являются приближением к идеальному алгоритму маршрутизации. Алгоритмы состояния каналов (алгоритм Дейкстры) позволяют каждому маршрутизатору получить необходимую информацию для построения точного графа сети. Маршрутизаторы выполняют маршрутизацию на основе однотипных графов. В связи с этим процесс маршрутизации оказывается более устойчивым к изменениям конфигурации [7]. «Широковещательная» рассылка производится только при изменениях состояния связей, что в надежных сетях происходит не так часто. Фактически, происходят небольшие корректировки по всем направлениям, в то время как алгоритмы вектора расстояний отсылают более крупные корректировки только в соседние маршрутизаторы.

Состояние линий связи (их стоимость), используемые для расчета кратчайших пу- тей [8], определяется следующей формулой:

C , = d , + S' + (1 - a ) S Q (l) + a S Q (I) , l l bl                           bl                  bl где dl - задержка передачи для линии связи l; bl -пропускная способность; Sp - размер (в битах) пакета данных, совершающего хоп; S q (1) - размер (в битах) очереди линии связи l; S е (l) -это экспоненциальное среднее размеров очередей линий связи и коррекций их действительного размера, исходя из того, что исследуется на данный момент. Коррекция определяется весовым коэффициентом, равным 0,4 [8]. Следует отметить, что способ вычисления C может быть произвольным.

Классификация метрик в алгоритмах маршрутизации

В алгоритмах маршрутизации используется различные показатели. Сложные алгоритмы маршрутизации при выборе маршрута могут использовать несколько показателей, комбинируя их таким способом, что в результате получается один отдельный (гибридный) показатель [9].

Основные показатели, которые используются в алгоритмах маршрутизации: надежность; задержка; ширина полосы пропускания; нагрузка; стоимость связи; длина маршрута. Важнейшими среди них являются задержка и полоса пропускания.

Задержка – отрезок времени, достаточный для прохождения информационного пакета от источника до пункта назначения через объединенную сеть. Задержка зависит от полос пропускания каналов сети, очередей в портах, промежуточных маршрутизаторов, перегрузки сетей на всех промежуточных каналах сети, физического расстояния, на которое необходимо переместить пакет. Задержка является общим и наиболее используемым показателем.

Полоса пропускания – отношение к мощности трафика определенного канала связи. Практически для любого вида трафика, физический канал технологии xDSL с полосой пропускания 2 Мбит/сек менее предпочтителен оптическому каналу с технологией FastEthernet 100 Мит/сек. Хотя полоса пропускания является оценкой максимально достижимой пропускной способности канала, маршруты, которые проходят через каналы с большей полосой пропускания, не обязательно будут лучше мар- шрутов, проходящих через менее быстродействующие каналы [10].

При оценке стоимости связи для построения эффективного маршрута важна не только эффективность передачи информационного пакета, но и затраты по передаче трафика по арендованным каналам связи. Предпочтительным считается отправка информационных пакетов через собственные линии, а не через линии общего пользования, даже, если задержка в них может быть значительно меньше, так как им придется платить за использованное время.

Нечеткие метрики «стоимости» маршрута

В описании объектов КС также появляются как четкие, так и нечеткие параметры. В процессе описания межсетевых процессов со стороны проектантов и администраторов КС появляются объективные и необъективные параметры, которые описывают передачу трафика и взаимодействие межсетевых процессов. К любой составляющей КС можно применить термин как «плохой канал», «быстрая линия», «медленный маршрутизатор», «хороший мультиплексор» и т.д.

Введены параметры, относящиеся к узлам маршрутизации: P r - пропускная способность маршрутизатора, Z r - задержка при передаче, S r - стабильность работы и параметры, относящиеся к каналам связи: P k - пропускная способность канала, S k -стабильность работы, Z_k – задержка.

Экспертом описаны каждые переменные с семью лексическими значениями на примере переменной S_r определяющей факторы, которые влияют на лексическое значение – перегрузка, нагрев, круглосуточный режим работы, погодные условия.

Таблица 1. Лингвистические термы нечеткой метрики S r

Лексическое значение	S r (max)	S r (min)
Очень большая	5 лет	3 года
Высокая	3 года	1 год
Большая	1 год	6 мес
Хорошая	6 мес	3 мес
Средняя	3 мес	1 мес
Низкая	1 мес	1 день
Очень малая	1 день	1 час

O k = f l   + f 2 S k + f 3 P k ,

Zk где f1 , f2, f3 – коэффициенты на основе нечетких характеристик канала.

Or = t1 17- + 12 Sr + t3 P , Zr где t1 , t2, t3 – коэффициенты на основе нечетких характеристик узла.

Общая оценка пути вычисляется следующим путем n           n—1

Op = Z Ori + Z Okj i=1           j=1

Каждая нечеткая величина O _r и O k , рассматривается как объединение трапециевидных нечетких интервалов параметров узлов и каналов. Каждый из этих нечетких интервалов M_i представлен пятеркой:

M{ = (m,mi,ai,ei,hi), где mi – нижнее модальное значение нечеткого интервала Mi; mi - верхнее модальное значение нечеткого интервала Mt; ai - левый коэффициент нечеткости; βi – правый коэффициент нечеткости; hi – высота нечеткого интервала.

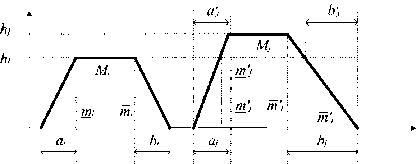
Рис. 1. Формирование нечеткой метрики

Нечеткая величина Mi+Mj, где Mi, Mj - два трапециевидных нечетких интервала (см. рис. 2.). Есть также трапециевидный нечеткий интервал (m , m ,а , в , h ), где h = min(hi, hj);

β=h

⎜^⎛β i + ^β j ⎟^⎞ ⎜_⎝h _i h _j ⎟_⎠

m = mi + mj- - ai - aj- + a;

Таким образом, общей метрикой маршрута является объединение нечетких величин параметров каналов связи и узлов маршрутизации, которые, в свою очередь, представляют собой объединение нечетких интервалов ФП каждой из локальных характеристик.

Представление структуры ВС нечетким гиперграфом

Нечеткий ориентированный гиперграф первого рода H = ( V , D ) будет являться адекватной математической моделью маршрутных таблиц при моделирования процесса маршрутизации в КС, если предположить, что множеству вершин V гиперграфа взаимно однозначно сопоставлено множество активных элементов I – узлов КС, а каждый маршрут прохождения по элементам j ∈ J представляет собой последовательность прохождения по множеству I и соответствует ориентированному ребру d j е D гиперграфа Н = ( V , D ) . Причем значения функции принадлежности μ _{d j} определяются, исходя из особенностей передачи информационных пакетов по каналам связи и обработки их в узлах связи.

Задача разбиения множества I активных элементов на определенные части по критерию предпочтения обработки информации активными элементами заключается в поиске разбиения множества вершин V, | V = n, на части V i , V 2 ,_ V k , где | V i | = n i , V! = n .... | V _k | = n _k , n ₁₊ n ₂₊_₊ n k = n , что сводится к последовательному разбиению множества V на два подмножества V 1 , и V ₂ = V \ V 1 .

Поскольку в каждом ориентированном ребре имеется существенная последовательность вершин, то можно перейти от каждого нечеткого ребра к однозначно представляющему его ориентированному графу, т.е. для каждого ребра d j гиперграфа H = ( V , D ) по строить нетет-кие ориентированные графы G ( d j ) = ( V , U j ) , где V = {v i }, i e I = {1,2,...n} - четкое множество вершин, U j = { < ц_и_ (v i , v k ) /(v i , v k ) > } - нечеткое множество ребер, где v i , v_k e V , M U . ( v i , v k ) - значение функции принадлежности μ_{U j} для ребра ( v i , v k ) .

Значения функций при разбиении множества вершин V на части V 1 и V ₂ будут определяться следующим образом.

\ M U j ( v a , ^v e ) ^фр- =1 0          .

Первая альтернатива верна, если:

^{( v} a G V1 &  v e e V2 ) V ( v a G V2 &  v e G Vi ) .

⎪⎧1,ϕPj ≠ 0 ψPj = ⎪⎩⎨0 j .

~.

Целевая функция ф ( H ) разбиения множества V на V ₁ и V ₂ будет выглядеть как

<№ ) =

m ^k j

∑ ∑ϕPj j=1 Pj =1

_m k _j

∑ ∑ψPj j=1 Pj =1

Выполняя разбиение, при котором значение целевой функции ф (H ) минимизируется, алгоритм формирует группы активных элементов I в КС, для которых можно определить оптимальный маршрут с предпочтительным временем обработки внутри выделяемой группы.

Поскольку в целевую функцию ф (Hl^-) входит нечеткость, то применять сложные методы в целях повышения точности разбиения маршрута считается нецелесообразным. Следовательно, использование алгоритма А1, при котором осуществляется последовательный выбор вершин из V , по выбранному критерию для включения в формируемую группу вершин ф (H ) является наиболее приемлемым.

Алгоритм маршрутизации с использованием нечетких метрик

Для поиска пути в КС предложено использование алгоритма A1 , который находит путь минимальной суммарной длины во взвешенном графе с неотрицательными весами (алгоритм Дейкстры) используется функция Min(F), которая возвращает вершину w е F такую, что справедливо равенство D[w] = min{D[v] | v е F}, что является нахождением кратчайших путей от данной вершины-источника до всех остальных вершин, перебирая пути в порядке увеличения их длин.

Вход алгоритма: сеть G = {V,E,c} заданная матрицей весов А порядка n ; выделенная вершина s . Выход алгоритма: расстояния D[v] — расстояния s от всех вершин v eV, где P[v] - предпоследняя вершина в кратчайшем (s,v) пути.

Допустим, что некоторые вершины v ∈ V на шаге t алгоритма уже вошли во множество V . Для произвольной вершины V f e V\ V будем использовать оценку Ф^, такую же, как и определение целевой функции, но характеризующую разбиение гиперграфа H при условии, что выделена группа вершин V 1t u{ v _f }. В итоге получаем:

m kj

_ϕ t _{P j}

,      1=1 £1    , где

^ ^{( v} f )=—

_{∑ ∑} ψ t_{P j}

j=1 Pj =1

\ Pu, ^{( v} a , ^v e )

=L

.

Первая альтернатива верна, если:

и ϕ _{P j} = 0 в противном случае,

⎪⎧1,ϕPt ≠0 ψP =⎨    j

j ⎪⎩0

~ P =< №j <  v a , v e >  / <  v a ’ vP >>  P j = 1, 2, 3 ... k

Каждую вершину v f характеризуем средним значением степени смежности вершин, образующих ребра, попадающие в разрез, в случае, когда вершина v f включена в формируемую группу V 1 .

В целях улучшения обработки значений внутри группы активных элементов для включения во множество V ₁ ^* необходимо выбирать ту вершину V v , для которой:

фt ( v v ) = min фt ⁽ v f ) .         (ф. 2..)

v _f ∈ V \ V ₁ ^t

Это позволяет утверждать, что на каждом шаге поиска формируется наилучшее – в смысле принятого выбранного критерия – подмножество элементов. Это приводит к получению оптимального разбиения множества V на V i и V 2 . Первая вершина, помещаемая в V ₁ , аналогично выбирается по ф. 2. При этом фактически берется вершина с наименьшим значением средней степени предпочтительности выходящих из нее ребер. Значение величины ф t ( v v ) вершины, помещаемой в V i , представляет собой значение целевой функции ф ( H ) при разбиении множества вершин V на V i и V 2 .

Сформулируем алгоритм выделения множества V i, содержащего n 1 , вершин (алгоритм А 2) и представим его в таблице 2.

Для выделения следующей группы активных элементов I из множества вершин V гиперграфа H =(V,D) производим удаление всех вершин в гиперграфе H сформированной части V 1 , а к оставшейся части гиперграфа применить алгоритм А 2. Процедуру повторяем до тех пор, пока не будут сформированы все группы активных элементов.

Таблица 2. Алгоритм А2 выделения множества активных элементов в нечетком гиперграфе

ШАГ
1.	Принимаем V 1 1 = ∅ по ф. 1 определяем ф ( v f ) для всех v f ^ V
2.	По ф. 2 определяем вершину v v
3.	Получаем множество V 1 1 включая v v t 0 в множество V 1
4.	По ф. 1 Определяем ф ( v f ) для всех vf ∈ V \ V 1t 1
5.	По ф.2 определяем вершину vv
6.	Получаем множество V 1 2 включая vv в множество V 1 1
7.	Если V1 t 2 = n1 , то значение ф ( v v ) равно значению целевой функции, а работа алгоритма закончена;
8.	Если V 1 2 < n 1 ,то принять V 1 2 за V 1 1 и выполнить шаг 4.

Структурно-функциональное решение автоматизации проектирования КС

Система моделирования маршрутизации КС, как программная система, подразделена на шесть основных блоков.

Интерфейсный блок (рис. 2) после выполнения процесса расстановки сетевых элементов взаимодействует с блоком исходных данных через модуль анализа и сохранения параметров и, в случае несвязности элементов сети, передает процесс моделирования модулю управления сетевыми компонентами для дополнительного моделирования несвязанных элементов. Блок исходных данных передает основные параметры сети блоку маршрутизации и параллельно блоку динамических данных, в котором используются дополнительные четкие и нечеткие параметры. Создается полная структура всех данных сетевых устройств и подсетей, межсетевых связей КС. Блок динамических данных передает структуру данных блоку маршрутизации для просчета маршрутов и блоку моделирования – для использования данных при формировании сетевого пакета и отсылки его по сети.

Блок маршрутизации (см. рис. 3), используя модуль формирования таблиц маршрутизации, взаимодействует с блоком алгоритмов, применяя математические инструкции для создания маршрутов в сетевых устройствах. После полного расчета таблиц маршрутизации в каждом сетевом устройстве управление передается блоку моделирования, где происходит конечный этап генерации сетевого трафика и посылки его по распределенной КС, учитывая все вложенности подсетей и передавая управление интерфейсному блоку, в котором проектанту визуализируются сетевые процессы и механизм прохождения пакетов в КС.

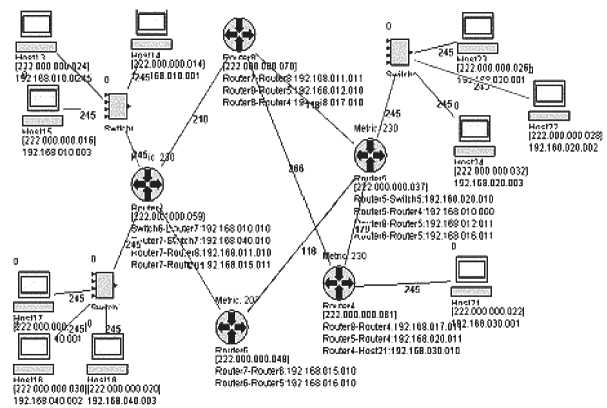
Рис. 2. Интерфейс блока описания структуры КС

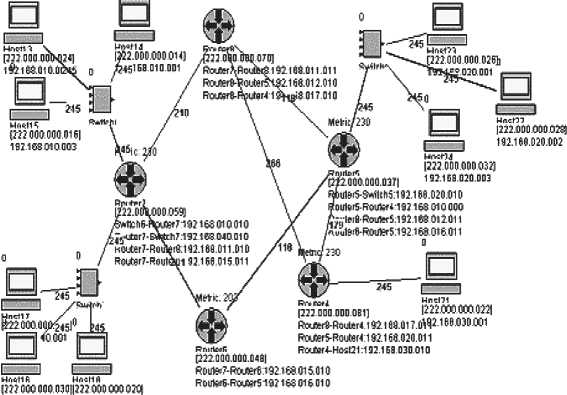
19 2.169 040 002 192.168.040.OD3

Рис. 3. Интерфейс блока маршрутизации

Результаты оптимизации трафика КС

Эксперименты были проведены в реальной КС ГУ ЦБ РФ по Ульяновской области. Полученные результаты были использованы при переконфигурации маршрутизаторов КС. Сегмент КС, в которой проводились эксперименты, был разделен на пять основных сетевых сообществ. В ходе вычислительных экспериментов была решена задача оптимизации трафика, который создавался на рабочих станциях соответственно.

Измерения были проведены с использованием программно-аппаратного анализатора трафика HP Internet Advisor J2300C. Рекомендации, полученные в ходе моделирования трафика на основе измерений с использованием нечетких параметров, были использованы при изменении таблиц маршрутизации.

Были проведены замеры трафика. Замеры трафика проводились до изменения таблиц в маршрутизаторах КС и после. Результаты измерений представлены в таблице 3. Оптимизированный трафик обозначен Т 1о . На рис. 4 изображена загрузка каналов связи до и после оптимизации.

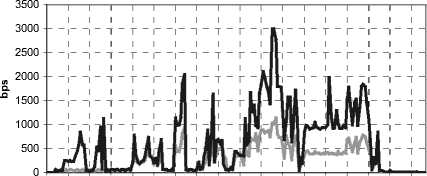
О 1   2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Time

^^^^^^^^еT1 - In ^^^^^^^^еT1 - Out

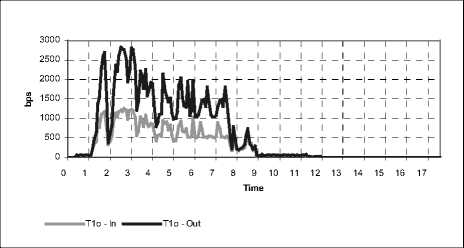
Рис. 4. Загрузка каналов связи трафиком до и после оптимизации

Измерения оптимизированного трафика Т1о показали, что время выполнения задач сократилось с 15 до 8 мин., а время работы приложения c 17 до 11 мин. Эффективность работы приложения наблюдалось уже со 2-ой мин., что отчетливо видно на диаграмме (рис. 4). Процент потери пакетов уменьшился на 3 %. Результаты замеров (таблица 3) показывают эффективность проведенной оптимизации трафика Т1. Формирование и моделирование общего трафика в корпоративной сети, состоящей из порядка 80 маршрутизаторов, 100 каналов связи, 40 серверов, может достигать 6-8 час. При использовании САПР КС на оптимизацию каждого трафика КС ГУ ЦБ РФ по Ульяновской области в одном сегменте было потрачено 6-7 мин. На описание объектов КС и наделение их сетевыми характеристиками потребовалось 12 мин. Общее время проектирования составило около 33 мин.

Таблица 3. Результаты измерений трафика до и после оптимизации

Трафик	Ti	Т1.
Время вы-	15 мин .	8 мин .
полнения задачи	25 сек	45 сек
Общее время	16 мин .	11 мин .
выполнения приложения	55 сек	50 сек
Общий исхо-	127215/	130851/
дящий	59442	64361
/входящий трафик	байт	байт
Занимаемая	2996/	2825/
полоса исхо-	1141	1243
дящего/ вхо дящего тра фика	бит/сек	бит/сек
Потери паке-	248/	220/
тов исходящего/ входящего трафика	98байт	76 байт
Процент по-	0,19/	0,17/
тери пакетов исходящего/ входящего трафика	0,16 %	0,12 %

Проектирование в САПР КС всех этапов осуществляется с помощью представления графа КС как гиперграфа и назначением гиперребрам, во вложении которых находятся целые подсети, общих нечетких параметров, что на порядок уменьшает время на описание сети, поведение трафика в котором предсказуемо или оптимизации не подлежит.

Отдельное проектирование одного из сегментов в САПР КС заняло 8 мин., других сегментов, соответственно, – около 18 мин., – около 6 мин., – 7 мин. Общее описание всех метрик элементов сети – 1 ч. 48 мин. Общее описание полной КС, представленной графом, – 2 ч. 50 мин. Полное затраченное время процесса составило около 12 мин.

Заключение

На сегодняшний день не существует протокола маршрутизации, который может использовать нечеткие данные (определенные экспертами, которые эксплуатируют КС) о составе оборудования, его поведении в разные моменты времени, качестве каналов, параметры местности, помещений эксплуатации. Однако, используя именно эти данные, САПР КС дает рекомендации по корректировке стандартных протоколов маршрутизации, которые осуществляются путем изменение маршрутных таблиц в маршрутизаторах. При оптимизации трафика в КС существуют этапы, когда необходимо оценить ситуацию в целой КС, и только потом оптимизировать более мелкие КС.

Используя систему автоматизированного проектирования КС, специалист может создавать наглядные проекты сетей, достаточно быстро их оценивать и динамически перестраивать, проводить предварительные эксперименты, не влияя на производственные процессы. Использование подобного инструмента ведет к существенному повышению качества эксплуатируемых КС.

Результаты экспериментов, произведенных в ходе исследования, подтверждают, что оптимизация с использованием предлагаемых моделей и методов дает лучший результат качества проектируемого объекта по сравнению с ручным проектированием.