Система моделирования с переменной структурой для прецизионных динамических объектов

Проблематика моделирования прецизионных динамических объектов

Моделирование служит основным методом автоматизированного проектирования технических объектов. В настоящее время хорошо развиты общие принципы построения систем моделирования, а также технологии их функционирования. Базовыми являются следующие принципы: модульность, визуальный или иной упрощённый ввод структуры моделируемой системы, автоматизация формирования модели системы на основе моделей отдельных модулей, возможность выбора численных методов решения полученных систем уравнений, автоматизация настройки этих методов (например, автоматический выбор шага в методах численного интегрирования) и др. Всё это делает современные системы моделирования удобным и надёжным инструментом исследования динамических объектов. Но это в полной мере относится только к сравнительно простым объектам, имеющим модели небольшой размерности при щадящих требованиях к точности вычислений. Обычно считается, что погрешность моделирования технических объектов до 10…15 % достаточна для практических целей.

Применительно к прецизионным техническим объектам это не так. Например, прецизионные электроприводы космических аппаратов (для систем поворота антенн или солнечных батарей) имеют допустимую погрешность позиционирования несколько угловых минут, что относительно полного оборота составляет доли процента [1-4]. Моделирование таких электроприводов с погрешностями до 10…15 % позволяет убедиться в работоспособности электропривода, но не дает возможность определить его точностные и динамические показатели, так как погрешность датчиков углового положения несоизмеримо мала по сравнению с погрешностью вычислений.

Для уменьшения погрешности повышают степень детализации математических моделей, стараясь учесть как можно больше особенностей физической реализации элементов моделируемого объекта: нелинейность, временнỳю и амплитудную дискретность, локальные динамические процессы в отдельных элементах с малыми постоянными времени, фронты импульсов и др. В результате вместе с точностью повышается сложность моделей, что влечёт за собой увеличение времени счёта. Особенно это заметно при наличии обратных связей в сочетании с нелинейностью математического описания и малыми постоянными времени. Применение обычных численных методов решения дифференциально-алгебраических уравнений приводит к тому, что приходится выбирать очень малый шаг интегрирования, процесс вычислений тормозится и время моделирования становится неприемлемо большим: сравнительно простые объекты могут моделироваться на обычных современных компьютерах в течение многих часов и даже дней.

Таким образом, при моделировании прецизионных динамических объектов имеется общая проблема: противоречие между точностью и временем счёта.

Для разрешения этого противоречия в существующих системах моделирования предлагается использовать автоматический выбор шага расчёта, а также распараллеливание вычислений. Оба этих подхода позволяют в ряде случаев добиться некоторого улучшения ситуации, но далеко не всегда.

В данной статье предлагается в дополнение к используемым методам реализовать другой подход к построению системы моделирования: в виде системы с переменной структурой. При этом предлагается использовать различные модели одних и тех же элементов – в зависимости от задачи моделирования и протекающих процессов. Если процесс не требует высокой точности расчётов для отдельных элементов, то можно использовать их упрощённые модели; если необходима высокая точность, то применяют более точные (и, соответственно, более сложные) модели. Вообще говоря, этот подход известен: именно так выбирают модели перед началом моделирования. Но в существующих системах моделирования структура и состав моделей остаются неизменными. В данном случае предлагается изменять структуру и состав моделей в процессе расчётов. Например, при позиционировании электропривода выделяются три стадии процесса: включение и разгон, движение с постоянной скоростью, торможение и точное позиционирование. При включении и разгоне электропривода достаточно использовать сравнительно упрощённые модели большинства элементов, а при приближении к точке позиционирования можно перейти к более точным моделям отдельных элементов. Смена моделей может приводить также к смене методов расчётов. Например, при переходе от упрощённой модели на основе алгебраических уравнений к более точной на основе дифференциальных уравнений требуется заменить численные методы решения алгебраических уравнений численными методами интегрирования. Возможны и другие ситуации, приводящие к смене метода расчётов.

Ниже рассматриваются основные принципы и связанные с этим проблемы построения систем моделирования с переменной структурой на примере моделирования прецизионных электроприводов космических аппаратов.

Программная реализация таких систем возможна с использованием существующих систем моделирования (например, Simulink пакета MATLAB) путём создания соответствующих тулбоксов. В перспективе можно будет реализовать систему моделирования с переменной структурой в виде самостоятельного программного продукта.

Принципы построения системы моделирования прецизионных объектов с переменной структурой

Система моделирования с переменной структурой в общем виде представлена на рис. 1. Здесь предусмотрено управление процессом моделирования путём изменения состава моделей и используемых методов.

С помощью Блока задания режимов моделирования задают входные воздействия, вид моделирования (численное интегрирование, расчёт установившихся процессов и т. п.), форму представления результатов моделирования и др.

С помощью Блока задания условий моделирования задают способы и условия смены структуры, т. е. моделей и методов. Возможны программное и следящее управления. При программном управлении задаются моменты времени, в которых происходит смена структуры. При следящем управлении задаются условия смены структуры в зависимости от значений перемен-

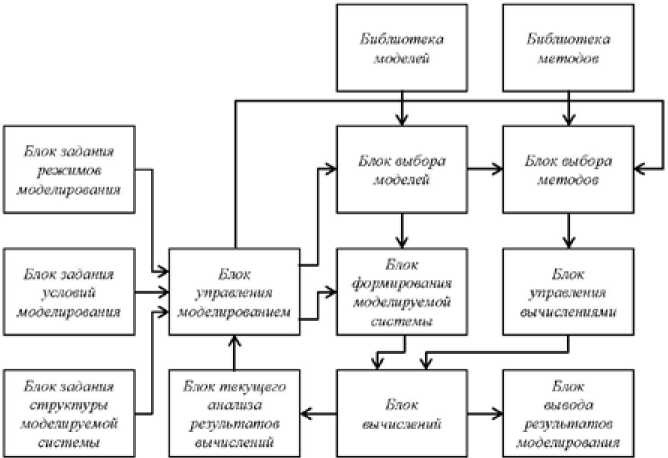
Рис. 1. Структурная схема системы моделирования с переменной структурой ных состояния и характера их изменения (быстрое, медленное, колебательное или др.). Также выбираются отрезки траекторий, на которых необходимо обеспечить максимальную точность или максимальную скорость вычислений. Условия могут формулироваться в терминах оптимального управления с заданием целевой функции и ограничений, в которых используются переменные состояния и входные переменные.

С помощью Блока задания структуры моделируемой системы задают модули и связи между ними, выделяют входы и выходы системы.

Библиотека моделей содержит для каждого элемента своё семейство моделей разной степени детализации (сложности) и, соответственно, точности.

Библиотека методов содержит подпрограммы (процедуры), реализующие различные методы вычислений: численное решение систем алгебраических уравнений, численное интегрирование, аппроксимацию, интерполяцию, преобразование математических моделей из одной формы в другую (например, передаточных функций в матричные уравнения переменных состояния) и др.

Блок управления моделированием выполняет изменение состава моделей и методов в процессе моделирования. Условия смены структуры заданы ранее в Блоке задания условий моделирования .

Блок выбора моделей осуществляет для каждого элемента подстановку моделей в соответствии с ранее заданными условиями по указанию Блока управления моделированием .

Блок выбора методов осуществляет выбор метода вычислений в зависимости от выбранной модели и, возможно, специальных указаний Блока управления моделированием .

Блок формирования моделируемой системы автоматически увязывает между собой модели отдельных модулей в единую систему уравнений. Эту функцию он выполняет постоянно – после каждой смены моделей.

Блок управления вычислениями оперирует методами, выбранными ранее в соответствии с используемыми моделями. Он обеспечивает необходимую последовательность вычислений, передачу данных между модулями.

Блок вычислений выполняет сами вычисления под контролем Блока управления вычислениями .

Блок текущего анализа результатов вычислений выполняет функции датчика и используется в случае применения следящего управления моделированием. В случае программного управления моделированием этот блок не используется.

Блок вывода результатов моделирования сохраняет результаты расчётов в файле, визуализирует их на экране в виде графиков, сохраняет в специальных файлах условия смены структуры системы моделирования, а также данные об этом в соответствующие моменты времени.

Предложенная структура системы моделирования соответствует обычному представлению объекта с точки зрения теории управления. Имеются входные задания и переменные состояния. Но в данном случае входными переменными являются желаемые показатели характера моделирования на различных его этапах: максимальная точность, максимальная скорость вычислений, ограничения. Результатом работы системы управления выступают показатели, полученные в процессе моделирования. Управляющим воздействием служит комплекс моделей и методов – их выбор меняет процесс моделирования. Таким образом, имеет место структурное управление объектом – с помощью изменения его структуры. В конечном счёте должны быть обеспечены максимизация точности и минимизация времени моделирования.

В данном случае нет возможности записать математическую модель системы моделирования как объекта управления в привычных понятиях теории управления – в виде алгебраических и дифференциальных уравнений. В результате нет возможности осуществлять формальный синтез управлений, которыми являются изменения структуры, – моделей и методов. Поэтому условия смены моделей и методов осуществляются пока из рациональных соображений.

Математические модели прецизионного электропривода для космических аппаратов

Примером технического объекта, моделирование которого предпочтительно с использованием предложенной системы, служит прецизионный электропривод для космических аппаратов. Он содержит электродвигатель, подсоединённую к его валу механическую нагрузку, подключенный к обмоткам двигателя источник питания, датчики и устройство управления. В качестве двигателей обычно используются синхронные двигатели с постоянными магнитами или индукторные двигатели (с электромагнитной редукцией) различных модификаций.

Управляющими воздействиями на систему моделирования, как это показано выше, выступают изменения структуры, включающей модели и используемые методы. В данном случае в качестве примера рассматривается возможность управления процессом моделирования изменением моделей двигателя и источника питания. Для этого разработаны комплексы моделей одного из типов двигателей – индукторного двигателя двойного питания (ИДДП), а также устройства электропитания – транзиторного коммутатора.

ИДДП имеет несколько вариантов математической модели различной степени детализации (различной степени упрощения) [7-9].

Исходная математическая модель ИДДП (включает две трёхфазные обмотки на статоре и безобмоточный ротор) в матричной форме имеет вид dψ

—— - -Ri + u,    V - LI, dt где ψ – вектор потокосцеплений обмоток; R – матрица сопротивлений обмоток; i – вектор токов обмоток; L – матрица индуктивностей обмоток; u – вектор питающих напряжений обмоток.

Здесь матрица индуктивностей содержит индуктивности, зависящие от угла поворота. Эти зависимости могут быть получены экспериментально [7] и представлены в виде табличных значений с последующей интерполяцией.

Далее возможны три варианта идеализации модели: с аппроксимацией индуктивностей косинусоидальными зависимостями; с допущением о геометрической симметрии (равенство углов между обмотками 120°); с допущением об электрической симметрии (равенство сопротивлений и собственных индуктивностей трёх фаз у каждой обмотки). Возможны различные комбинации допущений. Таким образом, получается не менее шести вариантов модели ИДДП в данной форме.

Модель ИДДП можно преобразовать в новую единую систему координат обмоток в системе относительных единиц:

d Vix                ,           , ,

—=- = ^-a i V i x + от , v i y + ^a i k 2 V 2 x + u iy ;

dt dViy                         ,    ,

—г²- = ^-OT i V i x ^{- a} i V i y + ^a i k 2 V 2 y + u i y ;

d V 2 x dt

= ^a 2 k i V ix - ^a 2 V 2 x + ^{( to} i ^- Ю r ) V 2 y + u 2 x ;

d V 2 y dt

= a2 kiViy - (to) -tor )V2 x -a2V2 y + u 2 y, где 1x, 1y, 2x, 2y – индексы (обозначения) первой и второй двухфазных обмоток в единой системе координат; ψ – потокосцепления соответствующих обмоток; u – напряжения питания соответствующих обмоток; ю1 = 2nf. - угловая частота питающего напряжения первой обмотки; f1 – частота питающего напряжения первой обмотки; ωr – угловая скорость ротора; α1, α2, k1, k2 – вспомогательные параметры, рассчитываемые через параметры обмоток:

R1        R2                   LmL

(Xi —----, (Х7 —-----,  с — 1 — kik?,  k =----, k? =

1 Lie’   2 L2C             121 L]     2

где R , R – активные сопротивления обмоток; L , L – собственные индуктивности обмоток;

L – взаимная индуктивность между первой и второй обмотками. ^m

Выражение электромагнитного момента

L

M = -ГГ- (V 1 y V 2 x - Y 1 x V 2 y ) .

σ L ₁ L ₂

Зависимость токов от потокосцеплений:

i 1 x = —( V 1 x - k 2 V 2x ) i 1 y = —( V 1 y - k 2 V 2y ) ;

Lyo i2x = —(V2x - k1V1 x) i2y = —(V2y - k1V1 y ) -

LyO

Приведённый вариант модели получен для применения всех рассмотренных выше допущений (косинусоидальная аппроксимация индуктивностей, геометрическая и электрическая симметрия). Ввиду этого данная модель является более упрощённой, чем рассмотренная выше матричная модель без допущений. Она позволяет выполнять численное интегрирование существенно быстрее, так как в ней отсутствуют тригонометрические функции, вычисление которых несколько замедляет расчёты. Но при этом не учитываются реальные параметры обмоток.

Полученная выше модель может быть дополнительно упрощена, если учесть характерное для всех типов ИДДП сочетание параметров. В частности, можно пренебречь взаимным электромагнитным влиянием обмоток:

d Vix

—1X^L =-« 1 V 1 x +® 1 V 1 y + u 1 y ;

d V 1 y

— «u x ^-a i _V i y + u i y ^;

™ = -« 2 ^ 2 x + (« 1 -® r )V 2 y + U 2 x ;

d V 2 y dt

<«   « r )V 2 x ^-a 2 V 2 y ⁺ u 2 y ,

где отброшены некоторые слагаемые: а 1 к 2 ^ 2_x = 0 , a i k 2 ^ 2 y = 0, a₂ £ м _x = 0 , a₂ £ 1 у 1 _y = 0 , так как величины α₁, α₂, k ₁, k ₂ малы (в системе относительных единиц они примерно равны 0,4…0,2) и их произведения представляют собой малые величины второго порядка.

Дальнейшее упрощение модели ИДДП может быть связано с пренебрежением изменениями электромагнитных величин во второй обмотке, если её напряжение питания не меняется в процессе управления:

,                 Г               2, , dVi x _ „ 1      a 2 k1k 2

----- - -ai 15-----------у

dt L    a 2 + (m i - го r )

V i x ⁺

a1a2kik2(toi- tor ) mi+ a 2+ (mi- m r)

Viy+

a i a 2 k 2 a 2 + (m i - m r )^

U 2 x 0 ⁺

^a i k 2 ^(m i ^{- m} rr )

--------2 U 2 y 0 ⁺ u ix ; a 2 + (m i - m r )

d ^V i y        , ^ai ^a 2 k i k 2 ^(m i ^{- m} r )

- - mi+

dt              a 2 + (to! - m _r) ²

V i x ^{- a} i

a ² ₂ k _i k ₂

ⁱ 2             2

a 2 + (m i - m r )

Viy-

^a i k 2 ^(m i ^{- m} r ) _T,     ,      ^a i ^a 2 k 2     _TI , „

-------72 U 2x0 +      -------72 U 2y0 + uiy , a 2+ (mi- m r)         a 2+ (mi- m r)

где U _{2 x 0} и U _{2 y 0} – амплитуды второго питающего напряжения, которые остаются неизменными (об этом говорит индекс 0).

Электромагнитный момент в этом случае

M =

Lm cLL2[a2+ (“1-“r) ]

x { ^[( “ 1 ^- to r^{) U} 2 x 0 ^{- a}2 U 2 y 0 ^] V 1 x ^{+ [(} “ 1 ^- “ r^{) U} 2 y 0 ^{+ a}2 U 2 x 0 ^] V 1 y ⁺

2     2

^{+ a} 2 ^k 1⁽ “ 1 ^- “ r ⁾⁽ V 1 x ⁺ V 1 y ) }

Аналогично этому может быть записана модель ИДДП в случае, если не меняется напряжение питания первой обмотки:

' - _J,_ '' kkг dt ~ "² [ ' a f + “Го

V 2 X ⁺

L aya₂ kk ₂ )

^{1 +} 2 ² 2 I “ 1-0 ^- “

I    a 1 + “ 20 )

V 2 y ⁺

a^ k 1 k2_И    «2 k 1 “ 1-0 _

+ “2----T- U1 x 0 + “2----T- U1 y 0 + u 2 X a1 + “1-0 a1 + “1-0

d V 2 y dt

L   a,a₂ k,k ₂ I

1 ⁺ 1 ² 122 I “ 1-0 — “

I    a 1 + “ 1-0 J

V2X - a2

a 2 k 1 k 2

1 2     2

^a 1 ⁺ “ 1-0

V2y -

a 2 k 1 “ 1-0 _p     «1 a 2 k 1 k2p

2----2^U 1 x 0 +       U-y 1 y 0 + u 2 y, a2 + “i-0        a2 + “i-0

где U _{1 x 0} и U _{1 y 0} – амплитуды первого питающего напряжения, которые остаются неизменными (об этом говорит индекс 0).

Электромагнитный момент в этом случае

L_m 2 2 a L i L 2 ^(a i + to i.o )

^[( ω 1.0^U1x0

^{- a} 1 ^ ¹ y0 ) V 2 X ⁺ № ¹ X ^{0 +} “ 1.0 ^ ¹ y0 )^ 2y 1 -

Возможно ещё более существенное упрощение, когда полностью пренебрегают электромагнитными процессами в обмотках. Тогда отсутствуют уравнения электрического равновесия и остаётся только выражение электромагнитного момента:

^Lm                                    2             2

^M =                       "^ "            "2? ^X{a 2 ^k 1 ® 2 ^U 1 m ^-a 1 ^k 2 “ 1 ^U 2 m -

J a L 1 L 2 l( a , a 2 a-^n 2 ) + ( a , » , +a 2 » , ) ^]

- U m. U 2 m ( a , a , a-» , » , ) . sin [ ₆ , - ( 0 , -0 , ) - ( _E , -_E , ) ] -

-(a,»2 -a2»,)• cos[9r -(9, -92)-(e, -e2)]}, где введены дополнительные переменные: θ1, θ2 – текущие фазовые сдвиги первого и второго питающих напряжений; ε1, ε2 – регулируемые фазовые сдвиги первого и второго питающих напряжений; U1m, U2m – амплитуды первого и второго питающих напряжений.

В случае пренебрежения малыми составляющими в полученном выражении электромагнитного момента оно дополнительно упрощается

При использовании пропорционального закона частотного управления можно записать ещё более простое выражение электромагнитного момента

M = jLL m ■ s^m( ⁶ r - ^e i ^{+ 6 2} - = i ⁺ = ² ) ,

UU где q i = m² , q 2 =   2m .

® 1         ® 2

Таким образом, от системы с шестью дифференциальными уравнениями можно постепенно перейти к одному выражению электромагнитного момента в алгебраической форме.

Далее рассматривается математическая модель устройства электропитания. Обычно в этих целях используется транзисторный коммутатор с широтно-импульсной модуляцией импульсного напряжения по синусоидальному закону. Но для ряда моделей необходимо представить его в виде источника идеализированного синусоидального напряжения:

где θ_{1 a} , θ_{1 b} , θ_{1 с} , θ_{2 a} , θ_{2 b} , θ_{2 с} – углы расположения обмоток соответствующих фаз.

В случае представления модели ИДДП в единой системе координат обмоток источник питания выглядит так:

ulx   U1 m cos(e1);

u l , = U 1 m sm(_{E 1} ^);

u 2x = U 2m ^cos(e 2 ^{+ E} 2 ^{- 6} 1 ^{+ 6} r )';

где угловые частоты питающих напряжений связаны с их текущими фазовыми сдвигами:

d θ        d θ

—¹ = toi , —² = to₂ .

dt ¹ dt ²

В действительности напряжение питания импульсное, что слабо проявляется при высоких частотах, но может быть заметно при низких. Поэтому при переходе на низкие частоты можно переходить к более точной модели широтно-импульсного преобразователя:

u1k= Um1.  , - 1, если    cos(9i + 8i + 9iь) > Пarccos[cos(0i J]; 1     1      1k 2                    1t π если    cos(0i + 81 + 01 k) < — arccos[cos(0it)], 2 r 1, u 2 k = Um 2 k' -1, . π если    cos(02 + 82 + 02k) > -arccos[cos(021)]; 2 если    cos(02 + 82 + 02k) < — arccos[cos(021)], 2 где k = a,b,c – индексы фаз;

d θ 1 t          d θ 2 t

—, = ^ro 1 t ; —,— = ^ю 2 t ; ® 1 t , ® 2 t - частоты опорных напряжений dt          dt

ШИМ для соответствующих обмоток; θ_{1 t} , θ_{2 t} – текущие фазовые сдвиги опорных напряжений ШИМ для соответствующих обмоток.

В результате будет сформирован широтно-модулированный импульсный сигнал напряжения, который весьма точно воспроизведёт форму настоящего сигнала, но при этом не учитываются внутренние параметры реального транзисторного коммутатора: односторонняя проводимость диодов, внутренние сопротивления диодов и транзисторов.

Математическая модель источника питания с учётом дискретного характера формирования питающего напряжения и внутренних параметров диодов и транзисторов приведена на рис. 2. Здесь показаны биполярные транзисторы, но аналогичную схему можно получить и для других типов транзисторов. Такой ключ устанавливается для каждой фазы, поэтому, например, для трёхфазного ИДДП с двумя обмотками будут использоваться шесть ключей – по три для каждого транзисторного коммутатора.

Транзисторный ключ можно представить в виде схемы замещения (рис. 3), на которой транзисторы заменены на идеальные диоды и ключи с сигналами λ на открытие и закрытие. Внутренне сопротивление транзисторов имитируется активной проводимостью G . Показана также зависимость проводимости от протекающего тока, что характерно для реальных транзисторов с их нелинейной вольт-амперной характеристикой. Аналогично представлены обратные диоды: с помощью идеальных диодов и активных проводимостей. Кроме того, в схему замещения введены ЭДС, которыми можно заменить падения напряжения на активных проводимостях.

Проводимости диодов и транзисторов определяются по следующим формулам:

Gd = A D ^ц i D1 ^ц = Bd^ ; в = 1 - 1/ ц;

Bd = A D ^Ц .

G T = A T ^£ i T ^{1 £} = B T i T ^;

a = 1 - 1/ e;              >

B_T = A T ^e .

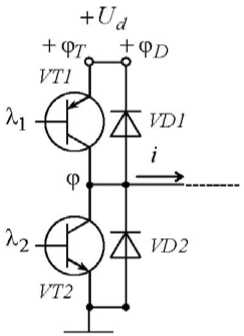
Рис. 2. Транзисторно-диодный ключ. Схема электрическая принципиальная

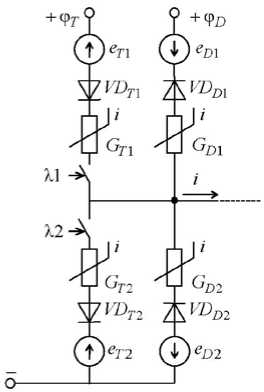
Рис. 3. Транзисторно-диодный ключ. Схема замещения

Таблица 1. Выбор параметров ключей транзисторного коммутатора

№	λ1	λ2	iK	G K 1	e K 1	G K 2	e K 2	φ K
1	0	0	>0	0	0	G D	eD	0
2	0	0	<0	G D	eD	0	0	φ D
3	1	0	>0	G D	e T	0	0	φ D
4	1	0	<0	G D	e D	0	0	φ D
5	0	1	>0	0	0	G D	eD	0
6	0	1	<0	0	0	G T	eT	0
7	1	1	>0	G T	eT	G T	eT	φ T
8	1	1	<0	G T	eT	G T	eT	φ T

Здесь коэффициенты μ и ε определяются из графиков вольт-амперных характеристик конкретных типов, соответственно, диодов и транзисторов.

Модель такого транзисторного коммутатора работает в соответствии с табл. 1. С её помощью определяются параметры ключей в зависимости от сигналов на открытие (или закрытие) транзисторов и направления тока. Всего возможны восемь вариантов сочетания параметров. Такая модель позволяет учесть как одностороннюю проводимость полупроводниковых приборов, так и их внутренние сопротивления (проводимости).

Полученные параметры подставляются в выражение для определения электрического потенциала φ на соответствующей клемме обмотки:

Г 1       1 )

Ф = Ф к - e K 1 - e K 2 - I             I ⁱK .

< G K 1 G K 2 )

Эта модель может быть упрощена следующим образом: можно приравнять нулю все внутренние сопротивления диодов и транзисторов (тогда останется только учёт односторонней – 807 –

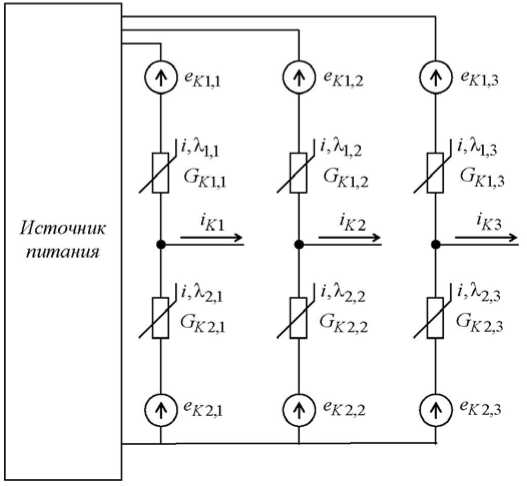
Рис. 4. Транзисторный коммутатор проводимости транзисторов и диодов); можно сделать сопротивления (проводимости) постоянными величинами (тогда будет проще считать падение напряжения на них), можно обнулить ЭДС. Таким образом, получаются ещё три варианта моделей транзисторного коммутатора.

Для трёхфазного транзисторного коммутатора используется схема замещения (рис. 4).

Математическая модель механической нагрузки в простейшем случае имеет вид dtor   1                d9r dt J1 sJ’      dt r, где ωr, θr – угловая скорость и угол поворота вала двигателя; J – момент инерции вращающихся масс нагрузки и вала двигателя; M – электромагнитный момент; M – статический момент нагрузки.

Более детальная модель может содержать, к примеру, составляющую вязкого трения, более сложный учёт статического момента (например, зависимость его от угла поворота) и т. д. При наличии редуктора или длинного вала возможен учёт упругости вала, его скручивание и т. д. То есть механическая нагрузка также может иметь несколько вариантов моделей.

Таким же образом можно разработать комплексы моделей для датчиков, устройств управления и других элементов электропривода [5, 6].

Проблемы реализации системы моделирования с переменной структурой

Видно, что каждая полученная модель обладает своим сочетанием достоинств и недостатков, некоторые процессы отражает весьма точно, а некоторые не отражает совсем. В действительности не всегда необходимо такое количество моделей с мелкими различиями, так как главное – это создание моделей, которые могли бы иметь существенные преимущества по простоте или точности по сравнению с другими моделями.

Характерно то, что модели различных элементов не всегда сочетаются между собой. Например, для двухфазных моделей ИДДП нужны двухфазные модели устройства электропитания. А модели транзисторных коммутаторов можно применять только совместно с трёхфазными моделями ИДДП в естественной системе координат. Поэтому создание модели одного элемента может повлечь за собой необходимость создания моделей других элементов, сочетающихся с первой. При этом новые модели других элементов могут не иметь преимуществ по времени счёта или точности, но они оказываются нужны для возможности использования первой модели.

Блок управления процессом моделирования должен знать, какие модели с какими сочетаются, чтобы выбор был адекватен поставленной задаче моделирования.

Динамическое изменение состава моделей приводит к проблеме сочетания переменных состояния: у новой модели состав переменных состояния может быть иным, чем у её предшественницы. Тогда необходимы специальные методы перехода от одной модели к другой. В некоторых случаях проблема решается сравнительно просто. Например, при переходе от модели ИДДП в естественной системе координат с шестью переменными состояния к модели в единой системе координат с четырьмя переменными состояния существуют формулы прямого и обратного пересчёта, что делает переход практически беспроблемным. Иногда имеется возможность просто обнулить те переменные состояния, которые больше не нужны в новой модели. Но в целом это специальная проблема обеспечения корректности перехода от одной модели к другой.

Заключение

Предложен новый подход к построению систем моделирования, который позволяет более эффективно разрешить противоречие между точностью и скоростью вычислений. Он заключается в построении систем моделирования с переменной структурой, когда в процессе моделирования в зависимости от исследуемого режима и задач исследования меняются модели элементов и методы их расчёта. В настоящее время реализация этих принципов проходит с применением существующих систем моделирования, позволяющих вводить сложные команды управления процессом: Simulink (для отладки алгоритмов моделирования) и MathCAD (для получения и отладки математических моделей в символьной форме).

Выявлены проблемы, которые необходимо решить для обеспечения корректной работы предложенной системы моделирования, рассмотрены некоторые возможности их решения. В перспективе предложенный тип системы моделирования может быть реализован в виде самостоятельного программного продукта.