Система оптимального проектирования лесовозных автомобильных дорог с учетом динамики лесосырьевой базы

BBEДEHИЕ

Сдерживающим фактором развития лесозаготовительной отрасли на Северо-Западе России является отсутствие развитой сети лесовозных автомобильных дорог. Строительство и содержание сети лесовозных дорог в силу почвенных и климатических особенностей региона являются дорогостоящими мероприятиями. Поэтому оптимальное планирование как непосредственно дорожной сети, так и этапов ее строитель- ства может существенно сократить расходы на строительство и издержки на содержание сети лесовозных дорог.

Анализ работ скандинавских исследователей [5], [6], [7] показал, что уровень развития сети ЛАД в соседних странах разительно отличается от российского, что не позволяет использовать зарубежный опыт напрямую. Скандинавские страны имеют существующую сеть ЛАД, которая поддерживается в актуальном состоянии,

и исследователи работают в направлении модернизации существующей сети, увеличения несущей способности дорог в межсезонье.

Из наиболее значимых публикаций по данной теме следует назвать работы [1], [3], авторы которых используют сходную методику для построения сети лесовозных автомобильных дорог. Но в используемых методиках не учитывается ряд факторов, а также сделаны различные допущения. В модели, представленной в [3], не учитываются рельеф местности, стоимость строительства при пересечении рек и болот. Серьезным допущением является построение сети дорог по точкам, соответствующим центрам укрупненных выделов. Это приводит к тому, что невозможно гарантировать оптимальность найденного решения и при строительстве дорог в него будут внесены значительные изменения. Методика, представленная в [1], построена на том же принципе: точками для построения графа дорог являются геометрические центры лесных кварталов. Методика также не учитывает особенности рельефа местности. Особенностью методики является ее практическая применимость, в модели заложены как запасы древесины, так и стоимость строительства дорог в различных условиях, учтены стоимости водопропускных систем. Целевой функцией в модели является функционал «доходы-расходы», что позволяет получать ответ на вопрос о максимальной прибыли с заданной лесосырьевой базы при минимальных затратах.

Таким образом, на данный момент существует методика построения сети ЛАД, учитывающая параметры как запасов лесосырьевой базы, так и стоимости строительства дорог. Основными недостатками данной методики являются: способ выбора точек для построения сети дорог, обеспечивающий малый набор точек, и отсутствие модели рельефа, которое может приводить к значительным корректировкам найденного решения из-за невозможности строительства дорог по критерию допустимого максимального уклона. Пути устранения этих недостатков будут рассмотрены в данной статье.

Особой задачей является строительство сети ЛАД с учетом динамики древостоя в перспективе нескольких десятков лет. Очевидно, что решения, обеспечивающие оптимальную дорожную сеть, с учетом исходных данных на текущий пе- риод и на долгосрочную перспективу будут отличаться. В данной статье описывается модель, учитывающая динамику древостоя и вариант ее реализации.

ЦЕЛИ И ЗAДAЧИ

Задача оптимизации текущей методики может быть разбита на следующие подзадачи:

• 1)    совершенствование используемых моделей;

• 2)    введение нового функционала. В рамках совершенствования используемых моделей будут рассмотрены следующие вопросы:

• •    введение модели, отображающей особенности рельефа местности;

• •    изменение модели, используемой для построения графа, отображающего сеть ЛАД.

Совершенствование методики по данным направлениям позволит находить более точное решение задачи построения оптимальной сети ЛАД. Введение нового функционала в методику заключается в разработке методов, учитывающих динамику лесосырьевой базы и позволяющих повысить экономический эффект от строительства лесовозных дорог.

MOДЕЛЬ РЕЛЬЕФA MЕСТHOСТИ

Описанная в [1] методика использует плоскую модель, состоящую из двух слоев: слой грунтов и слой гидрографии. В этой же работе рекомендуется включать слой рельефа для пересеченной местности. Рельеф местности должен быть учтен при расчете оптимальной сети ЛАД по следующим причинам:

• •    рельеф определяет возможность строительства дороги на данном участке исходя из максимально возможных допустимых руководящих уклонов;

• •    учет рельефа позволяет более точно оценить длину и стоимость проектируемого участка;

• •    возможность дополнительного задания условий на проектирование участков дорог: например, приоритет отдается участкам, проходящим по водоразделам.

Для этого в методику вводится модель рельефа местности. В модели определяются типы рельефа местности, характерные уклоны и коэффициенты удлинения трассы. Определение типов рельефа дано в табл. 1.

Таблица 1

Типы рельефа местности

Тип рельефа местности	Характеристика рельефа местности	Наибольший уклон поверхности земли	Наибольшее колебание отметок на 1 км, м
Равнинный	Ровные пространства, долины рек с пологими скатами, широкие спокойные водоразделы	1:15 (67 ‰)	≤30
Слабохолмистый	Мало расчлененный долинами рек, с отдельными редкими сопками и впадинами	1:10 (100 ‰)	<50
Холмистый (сильнопересеченный)	Местность сильно пересечена, водоразделы узкие, большое количество оврагов	1:5 (200 ‰)	<80

Значение уклона i (уклон - тангенс угла наклона) определяется по формуле tga = i = — = ен  ^, доли единицы, dd ip = i -1000, промилле (^о), где h - превышение одной точки над другой (высшей над низшей), м; Нон, Н^ч - проектные отметки конечной и начальной точек участка, м; d - горизонтальное проложение участка, м; i - значение уклона, промилле (‰). p

Руководящий уклон (‰) для веток имеет следующие значения: основные нормы – 40 ‰, в трудных условиях – 60 ‰, в особо трудных условиях – 90 ‰.

Степень отклонения трассы от воздушной линии характеризуется коэффициентом удлинения m , равным отношению фактической длины трассы L_ф к длине трассы по воздушной линии L_в

Lô m = —

L â

.

Значения коэффициентов удлинения трасс в различных условиях приведены в табл. 2.

Таблица 2

Ориентировочные значения коэффициента удлинения трассы в зависимости от категории сложности рельефа

Категория рельефа	Рельеф (тип рельефа местности)	Коэффициент удлинения трассы
1	Равнинный	1,1
2	Слабохолмистый	1,1–1,15
3	Холмистый (сильнопересеченный)	1,15–1,25

мо использовать иное множество вершин для построения графа. Множество вершин должно удовлетворять следующим требованиям:

• •    вершины распределены равномерно по рассматриваемой территории;

• •    среднее расстояние между смежными вершинами не превышает 250 м.

Для этого в ГИС необходимо создать слой, который будет содержать множество вершин, сгенерированных под заданные условия: например, это может быть квадратная сетка, узлы которой будут служить требуемыми вершинами. Естественным образом будут определены плоские координаты каждой вершины. Для того чтобы использовать модель рельефа, определенную выше, необходимо вычислить высоту ка-

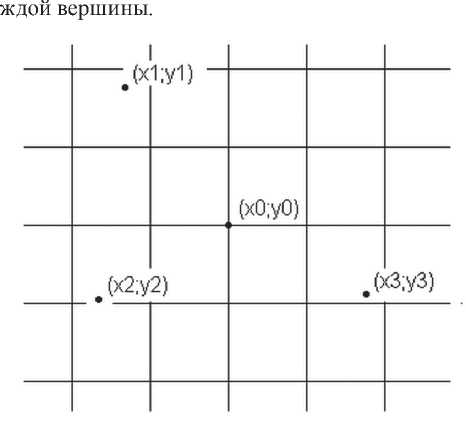
Рис. 1. Узел сетки и точки с известными высотами

Исходя из введенной модели возможно определить, подходит ли данный участок трассы для прокладки дороги, а также определить коэффициент удлинения трассы, который будет использован при расчете стоимости строительства данного участка.

MOДИФИКAЦИЯ MЕТOДИКИ ПOСТРOЕHИЯ OПТИMAЛЬHOЙ СЕТИ ЛAД

На данный момент методика базируется на решении задачи Штейнера на графах. В качестве вершин графа используются геометрические центры лесных кварталов. Это означает, что найденная оптимальная сеть дорог будет состоять из прямолинейных отрезков, длина которых будет сопоставима с размерами квартальной сетки (1–2,25 км). При построении лесных дорог такая сеть будет постоянно корректироваться, что неизбежно приведет к удлинению трассы и удорожанию ее строительства. Для того чтобы избежать большого объема корректировок трассы при прокладке и для более точной оценки стоимости строительства трассы, необходи-

Принимается допущение, что определяемая вершина лежит в одной плоскости с тремя ближайшими вершинами, высоты которых известны. Тогда высота вершины может быть вычислена исходя из следующих формул:

A = 1

y ₁

y ₂

y ₃

x ₁

h 2 , B = x 2

x ₃

1 h 1

1 h ₂

1 h ₃

x ₁

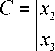
y ₁1

y ₂1

y ₃1

h о

x ₁

D = — x 2

x ₃

y ₁

y ₂ y ₃

h ₁ h ₂ h ₃

— D — Ax о — By о C

где ( x 1 ; y 1 ), ( x 2 ; y) ), ( x 3 ; y 3 ) - координаты точек с известными высотами h₁ , h₂ и h₃ соответственно, ( x₀ ; y₀ ) - координаты вершины, для которой определяется высота h₀ .

Для определения высоты произвольной вершины необходимо выбрать три ближайшие точки

с известными высотами. Выборка по данному условию может быть выполнена с помощью функций используемой ГИС MapInfo.

Таким образом, для всех вершин может быть рассчитана высота и впоследствии рассчитан уклон между смежными точками.

MЕТOДИКA ПOСТРOЕHИЯ СЕТИ ЛAД С УЧЕТOM ДИHAMИКИ ЛЕСOСЫРЬЕBOЙ БAЗЫ

На данный момент не существует методик построения оптимальной сети лесовозных автодорог, которые бы учитывали этапы и темпы строительства дорог и связывали бы их с динамикой лесосырьевой базы на рассматриваемом участке. Описанные модели работают в условиях, не привязанных ко времени. Запасы спелой древесины рассматриваются на момент построения модели; временные, а также финансовые ограничения на постройку дорог не учитываются.

Введение в методику средств, учитывающих динамику древостоя, позволит соптимизировать и разработать поэтапный план строительства сети дорог в долгосрочной перспективе.

Институтом леса Финляндии разработано программное обеспечение, моделирующее динамику лесосырьевой базы в условиях Северо-Запада. Благодаря ему можно получить прогноз по параметрам лесосырьевой базы на ближайшие несколько десятков лет, а также программу рубок ухода и основных рубок. Эти данные будут использованы для расчета сети дорог в описываемой ниже методике.

Задача построения оптимальной сети дорог с учетом динамики древостоя может быть решена при помощи ее декомпозиции на две задачи:

• •    задача об оптимальном размещении сети дорог с учетом параметров древостоя на текущий момент и прогнозируемых;

• •    задача об оптимальном порядке строительства участков сети дорог.

Данные задачи решаются последовательно. Решение первой задачи служит входным условием второй задачи.

Первая задача может быть решена с использованием существующих методик. Для этого на вход алгоритму, совершающему построение сети дорог, необходимо подать модифицированные данные по объемам разрешенной к заготовке спелой и перестойной древесины. Модификация входных данных производится следующим образом:

• •    выбирается период времени T (года), на который будет производиться расчет от текущего момента времени;

• •    для выделов на рассматриваемом участке местности производится моделирование динамики древостоя на выбранный период;

• •    выбирается подпериод T_k , на который будет разбит период T ;

• •    данные в каждый подпериод T_k заносятся новым слоем в ГИС-систему;

• •    создается новый итоговый слой в ГИС-си-стеме, в котором данные со слоев суммируются с данными подпериодов.

Например, выбран период T = 20 лет , подпериод T_k = 10 лет , таким образом получаем 3 слоя данных: на текущий момент, через 10 лет и через 20 лет. На рис. 2 буквами а, б и в обозначены слои со спелой и перестойной древесиной на момент расчета, через 10 лет и через 20 лет соответственно. Данные по запасам древесины суммируются в новом слое ГИС-системы (рис. 2г) и поступают на вход алгоритму, совершающему построение сети дорог. Используя входные данные, построенные указанным способом, алгоритм построит оптимальную сеть дорог, которая обеспечит максимальную отдачу от лесосырьевой базы за выбранный период времени.

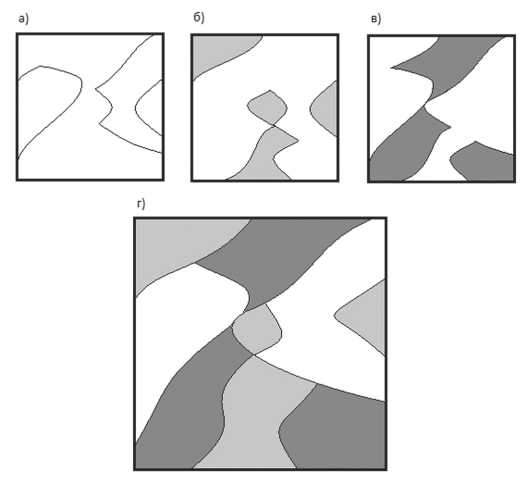
Рис. 2. Объединение слоев

Полученная сеть является входным условием для второй задачи, которая при заданных ограничениях формирует последовательность этапов построения дорог. В задаче рассматривается временной промежуток для одного этапа, равный одному календарному году. Могут быть заданы следующие ограничения.

• •    Максимальный объем заготавливаемой древесины за один год. Целевыми функциями алгоритма при этом могут быть: минимизация затрат на строительство дорог в год; распределение затрат на строительство дорог пропорционально заготавливаемым объемам; максимизация протяженности дорожной сети в первые годы строительства или иная целевая функция.

• •    Максимально допустимые затраты на строительство дорог в год (бюджет). Целе-

• вой функцией в данном случае будет выступать максимизация заготавливаемой древесины либо общей длины дорожной сети.

Выбор ограничения и целевой функции будет влиять на алгоритм решения данной задачи.

Остановимся подробно на ограничении годового бюджета на строительство дорог. Для решения задачи с данным ограничением необходимо выделить из рассчитанной сети все возможные подсети, которые могут быть построены с учетом ограничения бюджета на строительство. То есть необходимо найти множество поддеревьев графа сети дорог, удовлетворяющих ограничению. Из данного множества необходимо выбрать поддерево исходя из критерия целевой функции, например, выбрать поддерево, обеспечивающее максимальный возможный объем заготавливаемой древесины. Таким образом получаем решение, состоящее из набора участков дорог, которые должны быть построены в данном году. Для расчета решения для следующего года этот алгоритм применяется повторно, входными данными будет оставшееся дерево недостроенных участков дорог. Если оставшееся дерево разбивается на изолированные деревья, то оператору программного комплекса необходимо вручную распределить доступный бюджет между ними. Итогом работы рассмотренного алгоритма кроме плана дорожной сети также будет перечисление этапов строительства данной сети.

Рассмотренные в статье вопросы позволяют модифицировать имеющуюся методику построения оптимальной сети ЛАД с целью повышения точности производимых расчетов и актуализации получаемой дорожной сети. Функционал, учитывающий изменения лесосырьевой базы, позволяет оператору программного комплекса учитывать будущие запасы древесины на рассматриваемом участке и производить расчет и планирование работ на перспективу.

* Работа выполнена при поддержке международного проекта «Новые трансграничные решения в области интенсификации ведения лесного хозяйства и повышения степени использования топливной древесины в энергетике» ППС ЕИСП «Карелия» в рамках реализации Программы стратегического развития Петрозаводского государственного университета на 2012–2016 гг.

SYSTEM OF OPTIMAL LOGGING ROADS’ PLANNING FACTORING

IN FOREST RAW MATERIAL BASE