Система оптимального управления электроприводом станка-качалки

управления электроприводом постоянного тока. Получаемые в результате настроек внутренних контуров регулирования на технический оптимум [1, 2] передаточные функции регуляторов являются «стандартными»: для контуров регулирования тока и потокосцепления – пропорционально-интегральный регулятор, а для контура регулирования момента – интегральный регулятор.

Электропривод станка-качалки функционирует при наличии большого количества возмущений, оказывающих отрицательное влияние на работу оборудования. Эти возмущения связаны с изменением физикохимических свойств перекачиваемой пластовой жидкости, статической нагрузкой, создаваемой весом столба жидкости над плунжером, весом штанг и силами трения и проявляются в виде изменения тока (момента) нагрузки электропривода. Случайные изменения нагрузки приводят к возникновению механических нагрузок на насосное и электрическое оборудование, механическим ударам в системе, ступенчатому изменению числа качаний, увеличению значений пусковых токов и износу оборудования [1]. Поэтому при разработке системы управления электроприводом станка-качалки необходимо учитывать случайный характер возмущающих воздействий и использовать методы оптимального управления. Одним из центральных вопросов синтеза систем управления является обоснование критерия качества управления [3-5]. Системы автоматического регулирования скорости и расхода, функционирующие при действии случайных возмущений, заданных вероятностными или статистическими характеристиками, могут быть описаны выражениями следующего вида

A® (p)-® = B ю (p) • U ю+1 н (t)

,

AQ (P) • Q = BQ (P) • UQ +® Q (t)

где I н ( t ) – случайное изменение тока нагрузки электропривода в системе стабилизации скорости, ω Q ( t ) – случайное изменение скорости электропривода в системе стабилизации расхода насоса, ω , Q – регулируемые координаты электропривода, A ω ( p ), B B ω ( p ), A Q ( p ), B B Q ( p ) – операторные полиномы.

Так как значения случайных процессов I н ( t ) и ω ( t ) распределены по нормальному закону, то регулируемые координаты ω, Q также будут случайными процессами, распределенными по нормальному закону [1, 3, 6]. Тогда системы автоматического регулирования скорости электропривода и расхода насоса станка-качалки должны обеспечивать малые отклонения скорости и расхода от желаемых значений. Для этого необходимо минимизировать средние квадраты (дисперсии) отклонений скорости и расхода при случайных изменениях нагрузки или минимизировать среднеквадратические критерии качества управления:

1T

{to2) = lim — • J to2 (t) dt

\   / T w T 0

,

T

Q2 = lim 7 "JQ 2 (t)dt

T^T 0

,

где ^to 1 , QZ 1 - средние квадраты отклонения скорости электропривода и расхода насоса станка-качалки.

Необходимо учитывать, что один среднеквадратический критерий не отражает всех требований к системам управления. Реальные системы должны удовлетворять комплексу дополнительных требований, таких, как сохранение устойчивости при неизбежных вариациях параметров, реализация регуляторов без «идеальных» дифференцирующих звеньев и др. Учет дополнительных требований приводит к снижению предельных возможностей управления, и нужно стремиться к тому, чтобы эта потеря была минимальной.

Задача синтеза оптимальной системы управления приобретает смысл лишь при учете ограничений на управляющее воздействие. При бесконечной мощности управляющего воздействия можно обеспечить нулевую ошибку стабилизации. Для систем управления электроприводами ограничения обычно накладываются на модуль управляющего воздействия

U min <  U ( t ) < U max

,

что делает задачу оптимального управления нелинейной. В этом случае целесообразно перейти от ограничений на модуль управляющего воздействия к ограничениям на средний квадрат (мощность) управляющего воздействия

T

(U2) = '"my 'J U 2 (t) dt < NU

Ограничение (6) учитывается согласно правилам решения изопериметрических задач вариационного исчисления путем дополнения функционалов (3), (4) мощностью управляющих воздействий

J = X^ro²^

+ u ²^

J = x Q ²) + U²^

где λ – множитель Лагранжа, подлежащий в дальнейшем определению.

Уравнение движения электропривода станка-качалки при изменениях нагрузки представим в виде:

A ( p ) Q = U + 1 Э

где I Э = [ С , V 2 • K_M ( 4 y_T p + 1 ) ] I Н ( p ) -эквивалентное возмущающее воздействие, A ( p ) = K_M 4T.Jp ² + K_MJp +

M А Т M - операторный по- + K C = a 2 p ² + a 1 p + a ₀

л^ином, а 2 = ^K _M 4 T t ^J , a₁ = K M J , a 0 = K C ^-коэффициенты операторного полинома.

Центрированный процесс изменения тока нагрузки является стационарным процессом с нормальным законом распределения [1, 3], поэтому корреляционная функция аппроксимирована с учетом дисперсии следующим выражением

K, = Dr • e aT • cos Вт

IН      IН

где D_{I H} - дисперсия случайного изменения тока нагрузки.

Регулятор, полученный в результате синтеза оптимального регулятора скорости, должен быть физически реализуемым, т.е. не содержать звенья «идеального» дифференцирования. Для этого необходимо выполнение условия [3, 4]

pa n+g - 1,     (11)

4) Вводим в рассмотрение функцию

где 2 p и 2 g – степени числителя и знаменателя спектральной плотности возмущающего воздействия; n – степень полинома A ( p ).

Для выполнения условия (11) спектральная плотность эквивалентного возмущающего воздействия аппроксимирована выражением

i = G ( s ) • S i ( s ) =

F ⁽ s ) ^M 0 ⁽ s ^{) + M} + ⁽ s ) 5432

z 5 s + z 4 s + z 3 s + z 2 s + zx s + z 0

r3 s + r2 s + r s + r0

, (17)

Siэ (to)=Di

'      23         '      22         ' 2         '

Ьз (to ) + b 2 (to ) + bi to + bо d \ (to2 )2 + di to2 + d 0)

Выполнив деление полинома числителя на полином знаменателя функции (17), и выделяя целую часть, получим

Переходя к переменной s = jω и учитывая, что j ²=–1, получим

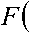
-X = a 2 s s )

+ z4

ar

s +

r3

z3

a2r1

z4

a2r2

S i э ⁽ s ) = d i э

- b 3 56 + b 2 s4 - bis2 + b0 d 2 s4 - d 1s2 + d 0

+

r3

r3

h 2 s2 + hi s + h 0

32     ,

r3 s + r2 s + r s + r0

Выполним синтез оптимального регулятора скорости электропривода станка-качалки по алгоритму, включающему следующие операции [3-5].

• 1)    Факторизуем спектральную плотность S / э ( s )

Sd (s )= Si (s )Si (- s ) =

b 3 s3 + b 2 s2 + bi s + b 0 - b 3 s3 + b 2 s2 - bi s + b 0 -----------------Z----------------------------------- • -------------------z------------------------------------- d 2 s2 + d 1 s + d 0         d 2 s2 - d 1 s + d 0

.                                             (14)

Полиномы числителя и знаменателя S 1 ( s ) будут содержать корни в левой полуплоскости, а

S i (- s ) - в правой.

• 2)    Факторизуем полином

A(s)• A(- s) + ^ = G(s)• G(- s) (15)

• 3)    Выполняем разложение на дроби следующего полинома

  A ^(- s ) G ( - s )

  
  

• Si (s ) = M 0 (s) + M +(s) + M -(s)

где M 0 ( s ) = A i s + A 2 - целый полином от

A 3 s + A 4

частного, ^M + ^{( s} ) = 3—2— ---- T" - дробь с

d 2 s + d i s + d 0

полюсами в левой    полуплоскости,

/ x     A5 s + A6

M -(s ) =---^---------- дробь с полюсами в c2 s - ci s + c0

• 5)    Определяем передаточную функцию оптимального регулятора скорости с учётом подстановки s = p :

W (p)= a0r32 - z3r3 + a2rir3 + z4 - a2r2

pc                            r ₃ 2

h 2 p ² + h i p + h 0

^- 3       2

r3 p + r2 P + ri P + r0

Как видно из выражения (19), передаточная функция оптимального регулятора не содержит «идеальных» дифференцирующих звеньев. Из анализа структуры оптимального регулятора скорости следует, что он может быть получен из «традиционных» регуляторов введением дополнительных звеньев, учитывающих случайный характер возмущающих воздействий.

Вывод: проведенные исследования оптимальной системы управления скоростью электропривода показывают, что дисперсия выходной координаты в 1,5-2 раза меньше по сравнению с традиционными системами управления [3-5].