Система оптимальных планов производства с учётом влияния относительной нормы выпуска двух видов продукции

В статье [1] были рассмотрены планы производства двух видов продукции с использованием двух ресурсов, в котором учитывалось влияние двух видов нормы выпуска продукции. В качестве таких норм были выбраны: норма на минимальное отношение объёмов выпуска продукции первого вида ко второму (минимальная относительная норма первого вида продукции ко второму) и норма на минимальный выпуск продукции второго вида (минимальная норма выпуска второго вида продукции). Для найденных планов в [1] в статьях [2-9] был проведён анализ решений задачи при различных рыночных условиях. В статьях [2-5] был проведён анализ оптимального плана, когда полностью расходовались оба ресурса и продукция выпускалась по обеим нормам. В статьях [6-9] рассматривались оптимальные планы выпуска продукции, при которых либо один ресурс не расходовался полностью, либо продукция выпускалась только по одной из двух норм. В работах [2] и [6] анализ был проведён для производства с приоритетным выпуском продукции первого вида, в [3] и [7] - для производства с приоритетным выпуском продукции второго вида, в [4] и [8] - без приоритета выпуска продукции, в [5] и [9] - в особых рыночных условиях.

На основе проведённого анализа решения пары двойственных задач в работах [10-13] были исследованы системы оптимальных планов двойственной задачи для каждого рыночного условия и построены сетевые графики при равенстве во всех ограничениях прямой задачи: в статье [10] при приоритете выпуска первого вида продукции, в статье [11] - второго вида, в статье [12] - без приоритета, в статье [13] - в особых рыночных условиях. В статье [14] построены сетевые графики для планов, в которых отсутствовало влияние одного из факторов в условиях приоритета выпуска продукции первого вида.

1.    Цель и задача исследования

В данной работе построим сетевые графики оптимальных планов, в которых отсутствует влияние одной из норм производства, если рыночные условия способствуют приоритету выпуска второго вида продукции.

2.    Методология, методы и методика исследования

Задача исследования, терминология и обозначения будут использоваться такие же, как и в статьях [10-14]. Модель экономической задачи влияния норм выпуска продукции представляет собой задачу линейного программирования и построена на основе методологии математического моделирования.

Анализ её решения предполагает использование теории двойственности в линейном программировании. Анализ исследуемой задачи проведён в работе [3].

Построение сетевого графика будем осуществлять, используя методику построения сетевых графиков в теории графов.

3.    Результаты исследования

Методика построения системы оптимальных планов, которые формируются на основе решения частных задач при частных значениях параметров решений была рассмотрена в работах [10-14]. Мы подробно не будем останавливаться на формулировке понятий задачи в этой методике, а сразу рассмотрим решение поставленной задачи.

Двойственная задача представлена в работах [1, С. 25] и [15, С. 547] и имеет вид:

• 1)    равенствами являются ограничения

для минимальных норм и одного из ис- пользуемых ресурсов,

• 2)    равенствами являются ограничения по использованию обоих ресурсов и по минимальной относительной номе выпус-

• ка продукции первого вида ко второму.

• 3.1.    Оптимальные планы влияния

обеих норм и одного из ресурсов

В двух оптимальных планах наблюдается влияние обеих норм и использования одного из ресурсов. Первый из них план, когда наблюдается влияние только ресурса

R 1 имеет вид [11]:

и 1 *=— • ^Г^Т • t, u 2 *=0, и 3 *=-^ Ст-¹ • “и ^o+^i                    V^o+ki

—1, и ₄ *= —d/30+к—1 , (2)

где ≥ 1. Это общее решение является множеством планов T (1; 0; 1; 1).

Во втором плане наблюдается влияние только ресурса R ₂ имеет вид [11]:

+     +

+     -

>^{С 1}   (1)

+   ≥

и 1 *=0, и 2 *= ^- • А^-^ • 5, и 3 *=-С 1 “21 Ро+Кг

Ро+к , -Ро+к₂

—-1, и ₄ *= —cl flO+k—-!, (3)

иг > 0 и2 > 0 из < 0  и4 < 0

W =   Ь и^  +b₂и₂     +пи₄  ^ тin.

При исследовании будем использовать дополнительные коэффициенты в модели, которые были предложены в работе [1, С. 25]. Это коэффициенты к ₁ =^ ²- , к ₂=— и

“и a₂i к А

С1

Условие предпочтение выпуска второго вида продукции предполагает, что к > к ₂ .

Анализ оптимальных планов, проведённый в работах [1, 3, 7, 11], экономический анализ в статьях [16, 18] и формирование управленческих решений [17] показал, что при приоритетном выпуске продукции второго вида влияние трёх факторов наблюдается в оптимальных планах, в которых:

где ≥ 1. Это общее решение является множеством планов T (0; 1; 1; 1).

Построим сетевые графики для каждого из решений по отдельности.

• 3.1.1.    Оптимальные планы влияния обеих норм и первого ресурса

Смотрим первый план (2). В нём продукция обоих видов выпускается по относительной норме в 0 , продукция второго вида по норме n и ресурс R 1 расходуется полностью. Граничное значение параметра t одно: t = 1. Подставляем его в решении (2). Получаем:

и 1 *=—, и 2 *=0, и 3 *=-Си • -^^S и 4 *=0.(4) ац                 Ро^+К1

Это решение составляет множество T (1;0;1;0). Значит,

T (1;0;1;1)^ T (1;0;1;0).  (5)

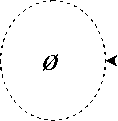
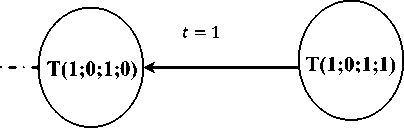
Рис. 1. Сетевой график оптимальных планов при влиянии обеих норм и использования ресурса R 1

Множество T (1;0;1;0) предшествует 0. Получаем сетевой график (рис. 1).

• 3.1.2.    Оптимальные планы влияния обеих норм и второго ресурса

Рассмотрим план (3). Теперь полностью расходуется ресурс R ₂ . Граничное значение параметра s : s = 1. Получаем:

U 1 *=0, и 2 *=^-, и ; *=— С_г • ^ ^k2 , Щ*=0.

^{1     ,   2}    «2 ?    ^{3       1} 0 + +^к2    ⁴

Это множество T (0;1;1;0), поэтому

T (0;1;1;1)^ T (0;1;1;0).  (7)

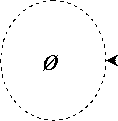
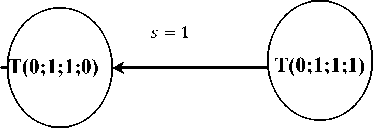
Рис. 2. Сетевой график оптимальных планов при влиянии обеих норм и использования ресурса R 2

Множество T (0;1;1;0) предшествует 0 . Получаем сетевой график (рис. 2).

• 3.2.    Оптимальные планы влияния нормы выпуска второго вида продукции

Рассмотрим оптимальные планы в которых наблюдается влияние минимальной относительной нормы продукции первого вида ко второму в о и использования обоих ресурсов. Общее оптимальное решение для таких планов имеет вид [11]:

и 1*=^ ^ и     .  ' S, и 3*=-

к-к г        к-к2  „

---t + ---S 0О ^{+ к}1      0О^+к2

где t >0, s >0, t + s =1.

Это общее решение является множеством планов T (1; 1; 1; 0).

Здесь два граничных значения параметров: t =0 и s =0.

Сначала в (8) подставим t=0, тогда s =1, получаем:

и 1 *=0, и 2 * = ^С1( _г ^к+0 О ⁾ Л , и 3 *=0, и 4 *=-C i (k₂ - « 21^(к2 ^Р 0 )

к).     (9)

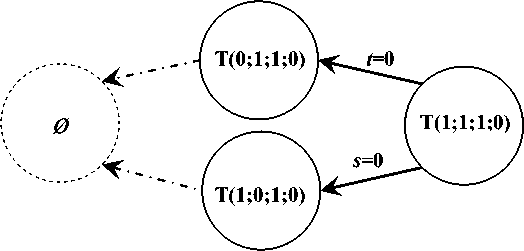
Рис. 3. Система оптимальных планов при влиянии относительной нормы продукции

Это множество T (0; 1; 1; 0). Значит,

T (1;1;1;0Н T (0;1;1;0).  (10)

Теперь в (8) подставим 5 =0, тогда t=1, получаем:

• >/,*=——^^о+к 7/₇*=о ид*=—Ci ■ ^{к к2} u¹   «ц ^_o+kl’ u^{2   0}’ u^{3     C1}Po+k₂”

4. Выводы

U 4 *=0. (11)

Это множество T (1; 0; 1; 0). Значит, T (1;1;0;1)^ T (1;0;1;0).  (12)

Оба множества предшествуют ø . Получаем сетевой график (рис. 3).

В работе системы оптимальных планов для производства, использующем два ресурса, при влиянии норм выпуска двух видов продукции в рыночных условиях с приоритетом выпуска первого вида продукции. Связи решений представлены в виде сетевых графиков (рис. 1-3).