Система поддержки принятия решений на основе многоатрибутивных методов

Использование многоатрибутивных методов принятия решений при проектировании бортовой системы космического аппарата позволяет учесть возрастающие тактико-технические требования к бортовой аппаратуре и перспективные тенденции развития современной электронно-вычислительной аппаратуры, а также значительно сократить время разработки и оптимизировать финансовые затраты [1].

В СППР реализуется модифицированный метод упорядоченного предпочтения через сходство с идеальным решением (TOPSIS), преимуществом которого является возможность решения задачи принятия решений при бесконечном числе альтернатив. Оба критерия – «наикратчайшее расстояние до позитивного идеального решения» и «наибольшее расстояние до негативного идеального решения» – заменяются на «как можно ближе к PIS» и «как можно дальше от NIS». Термины «как можно ближе» и «как можно дальше» – нечеткие, и, чтобы их смоделировать, применяются функции принадлежности из теории нечетких множеств: d_p ^PIS (уступки) и d_p ^NIS (поощрения) – расстояния до PIS и NIS соответственно.

Вместо k исходных целей будем использовать цели «минимизировать расстояние до PIS d_p ^PIS » и «максимизировать расстояние от NIS d_p ^NIS ». Получим задачу: min d_p ^PIS ( x ); max d_p ^NIS ( x ), х ∈ Х.

В связи с тем, что эти две цели обычно конфликтуют друг с другом, невозможно одновременно достичь их индивидуального оптимума. Каждая цель достигает только части своего оптимума. При детальном рассмотрении функции принадлежности m₁( х ) и µ ₂( х ) – это две невозра-стающие/неубывающие монотонные функции между точками экстремума ( d _p ^PIS ) ^* и ( d _p ^NIS ) ^* . Функции m₁( х ) и m₂( х ) показывают степени предпочтения «как можно ближе к PIS» и «как можно дальше от NIS».

Компромиссное решение х ^* достигается решением задачи max{min[ µ ₁( x ), µ ₂( x )]}.

Используемый fuzzy-метод фактически переформулирует задачу многоцелевого принятия решений как задачу нечеткого программирования. Пользователь получает возможность сгенерировать недоминируемое множество решений.

Реализуемый в предложенной системе метод учета неопределенности и субъективности оценок при выборе недоминируемого решения учитывает не только неопределенность в оценках ЛПР, но и его интуитивные склонности относительно реальных характеристик атрибутов и их специфики [2].

Метод рассматривает т альтернатив, представляющих собой различные составы бортовой системы, из которых необходимо сделать выбор. Каждому выбору соответствует п значений атрибутов.

Согласно концепции «идеальной точки», обозначим через А ^* ( x ₁ ^* , x ₂ ^* , …, x_n ^* ) «идеальную» альтернативу, для которой x_i ^* предпочтительней x_i ^{( k )} (атрибут альтернативы А ^{( k )} ) для любых k и i . Отметим, что некоторые значения x_i ^* могут и не соответствовать значениям атрибутов альтернатив А ^{( k )} рассматриваемого множества.

Обозначим субъективную оценку относительной важности каждого i -го атрибута с помощью нечеткого множества Н_i , Н_i описывается своей характеристической функцией вида f_Hi : H_i → [0,1], которая характеризует предпочтительность А ^{( k )} по i -му ат рибуту. Очевидно, что f_{H i}( x_i ^* ) = 1, так как x_i ^* – наилучшее возможное значение i -го атрибута.

Выбор альтернативы представляет собой попытку минимизировать «расстояние» между А ^{( k )} и А ^* , которое является функцией субъективных предпочтений, характеризующих квалификацию, опыт практической работы, уровень знаний о предметной области, а также зависит от уровня информированности о представленном для выбора реальном множестве альтернатив в конкретной ситуации.

Благодаря сгенерированным коэффициентам в процессе выбора учитывается неопределенность, присущая данной задаче. Очевидно, что если для всех x_i ^{( k )} (1 ≤ k ≤ m ) на этапе принятия решения информация о предпочтительности недоступна (скрыта), то неопределенность по i -му атрибуту становится относительно высока. Однако высокий уровень для x_i ^{( k )} и низкий для x_i ^(l) , где k ≠ l, снижает неопределенность по i -му атрибуту. В решающем алгоритме применяется наиболее часто используемая мера неопределенности – энтропия.

Чтобы выразить нечеткое множество Н_i , определяется оценка степени принадлежности элемента x _i ^{( k )} этому нечеткому множеству. Это позволяет найти в дальнейшем неопределенность по i -му атрибуту как функцию энтропии е_i .

В расстоянии между двумя альтернативами весовые коэффициенты, зависящие от неопределенности, будут малы, если неопределенность высока. Определяем коэффициент сатисфакции по i -му атрибуту S i . Когда неопределенность, соответствующ а я i -му атрибуту, высока, то е_i близко к 1 и коэффициент S мал.

При относительных весах по важности w_i , назначаемых ЛПР i -му атрибуту априори, можно определить весовой коэффициент, комбинирующий нечеткость и субъективную оценку.

Для того чтобы определить, насколько удалены друг от друга альтернатив ы А ^{( k )} и А ^* введем функ цию расстояния Dis[ A ^* , A ^{( k )} ] = ∑ ⁿ ( S_i ⋅ (1 - f_Hi ( x_i ^{( k )} ))) ² . Значение i = 1

Dis( А ^* , А ^{( k )} ) соответствует среднеквадратичному отклонению Dis ^{( i )} . Нашей целью является выбор альтернативы A ^{( k 0)} , котор ая максимально близ ка к A ^* : Dis[ A ^* , A ^{( k 0)} ] = Dis _k ^min [ A ^* , A ^{( k )} ].

Процедура выбора недоминируемого решения, основанная на субъективных предпочтениях ЛПР, выглядит следующим образом.

Шаг 1. Назначение идеальной альтернативы. Представление пользователю всех имеющихся недоминируемых альтернатив.

Шаг 2. Назначение пользователем f_Hi ( x_i ^{( k )} ) характеризующих предпочтительность k -й альтернативы по i -му атрибуту для ∀ k , i . Назначение весовых коэффициентов w_i , определяющих относительную важность i -го атрибута.

Шаг 3. Определение наилучшей альтернативы путем выполнения следующих вычислительных процедур:

• –    расчет частных энтропий по каждому атрибуту е_i ∀ i ;

• –    расч е т коэффициентов сатисфакции по каждому атрибуту S _i ∀ ;

• –    расчет весовых коэффициентов S _i i , комбинирующих нечеткость и субъективную оценку;

• –    расчет значений Dis ^{( i )} для ∀ i , определяющих расстояние между k -й альтернативой и идеальной альтернативой по i -му атрибуту;

• –    расчет Dis( А ^* , А ^{( k )} );

• –    определение наилучшей альтернативы путем минимизации Dis( А ^* , А ^{( k )} ).

Шаг 4. Предоставление ЛПР значения Dis( А ^* , А ^{( k )} ) и соответствующего ему решения. Если полученное решение удовлетворяет ЛПР, то завершение, иначе – переход на Шаг 1 [3].

Рассмотрим концептуальную схему системы поддержки принятия решений, основанную на приведенных методах (см. рисунок).

Программное приложение реализовано на языке С++ с использованием средств визуального программирования приложений Borland C++ 5.0. Это позволило наиболее полно использовать возможности, предоставляемые объектно ориентированным подходом в программировании, а также наиболее качественно разработать графический интерфейс приложений, работающих под управлением операционной системы Microsoft Windows от версии 3.1 и выше.

Система работает с пользователем (оператором) в интерактивном режиме. Пользователь сам выбирает метод вычисления. Также он может контролировать любые изменения параметров и изменять настройки системы и исходные данные.

Анализ работы СППР показал, что наилучшие результаты работы алгоритма проявляются при параметре р = 2.

Для исследования работы алгоритма fuzzy-метода в условиях поставленной задачи использовались различные начальные данные (значения стоимости и надежности предлагаемых блоков, требуемая глубина резервирования и др.). Проводится анализ работы метода в зависимости от таких данных, задаваемых ЛПР, как предпочтительность критериев и разность между суммой глобальных и действительных процентов достижимости по всем целям.

Fuzzy-метод генерирует недоминируемое решение на основании заложенной в него информации о следующих параметрах: количестве типов блоков; количестве вариантов каждого типа блоков; количестве и виде принятых к рассмотрению критериев эффективности; значении характеристик (в данном случае – стоимости и надежности) предлагаемых вариантов блоков; требуемой глубине резервирования блоков.

С помощью fuzzy-метода ЛПР, изменяя значения параметров, может получить недоминируемые решения,

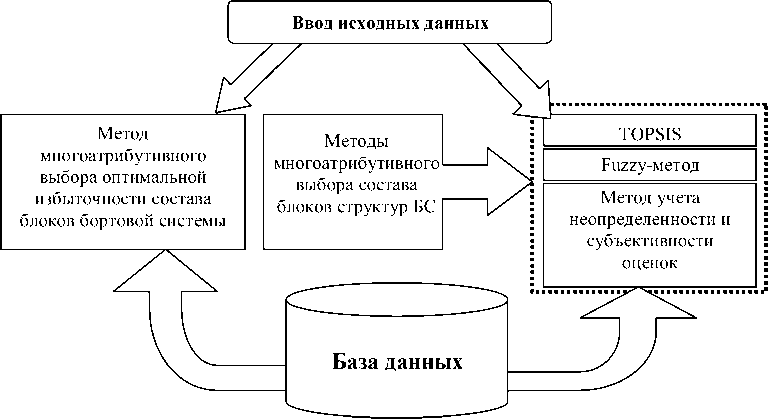
Концептуальная схема СППР

из которых можно сформировать множества различной мощности. При необходимости в процесс формирования множества недоминируемых решений может включаться несколько экспертов.

Процедура метода учета неопределенности и субъективности оценок выделяет из этого множества одно решение, основываясь на индивидуальных предпочтениях ЛПР. Выбор среди нескольких альтернатив осуществляется, основываясь на значениях следующих параметров, заданных ЛПР: предпочтения альтернатив по каждому критерию f_Hi ; весовых коэффициентов атрибутов w_i [4].

Проведенные исследования показывают, что увеличение мощности множества недоминируемых решений может вести к улучшению решения, однако с другой стороны, его увеличение нецелесообразно тогда, когда пользователь не в состоянии дать непротиворечивую оценку всем предоставленным ему альтернативам.