Система показателей эффективности и достоверности контроля при мониторинге

ВВЕДЕНИЕ                      Проблема контроля и диагностики медицин-

Анализ и оптимизация качества контроля по целевому критерию предназначены для реализации контроля за одним или группой параметров в динамических системах различного характера и являются важным элементом медикотехнических исследований, в частности в проблеме медико-биологического обеспечения стендовых испытаний образцов аэрокосмической и глубоководной техники. Объектом контроля здесь выступают человек (оператор-испытуемый) или параметры среды, особенно в условиях замкнутых объемов с длительным циклом автономного жизнеобеспечения. Задачей является слежение и сопоставление с нормативными градациями контролируемых параметров (КП) за время, соизмеримое с длительностью автономной эксплуатации реального объекта, а также накопление базы данных, включающей результаты синхронной регистрации параметров динамики управления и оперативнотактической нагрузки испытуемых на стенде-макете изучаемого технического объекта [1–5].

Наблюдаемыми и контролируемыми параметрами (НКП) служат показатели функционального состояния операторов (частота сердечных сокращений и частота дыхания, энцефалограмма, кожно-гальванический рефлекс, миограмма (показатели речи), показатели уровней загрязнения среды (концентрации вредных веществ, уровни газовы-деления синтетических конструкционных материалов и продуктов жизнедеятельности человека в гермообъектах).

ских показателей и уровней загрязнения среды типичны в задачах мониторинга, включая контроль выбросов [6]. В общей методологии заключения о качестве состояния объекта по НКП пока редко применяются принципы допускового контроля, т. е. установление такого коридора вокруг нормативного уровня НКП, который приемлем на основе того или иного концептуального представления о целевом критерии контроля [7, 8]. Особо важен такой подход, например, при создании системы контроля в условиях тренажа с планируемыми субэкстремальными уровнями факторов воздействия на человека. Традиционные методы контроля, основанные на принципе "если НКП меньше норматива — хорошо, если превышает, то — стоп", не обеспечивают полностью адекватность решения задач контроля [1, 2, 9]. Это подтверждает и современная тенденция создания новых принципов управления на основе концепций гибкой (или размытой) логики.

Точно так же, по-видимому, обстоит дело и с контролем технических систем. Выбор жесткого норматива на НКП приводит к установлению необоснованно высоких уровней допуска на группу НКП или, если такого завышения уровней контроля не делать, то возникает ситуация частого превышения одним из НКП допустимого уровня и как следствие требование на обслуживание объекта. Незначительно улучшает ситуацию и введение плавающих в определенных пределах дифференцированных допусков для группы НКП [10–12]. Стремление удовлетворить допусковые пределы всех НКП приводит к требованию расширения коридора разрешенных отклонений от норматива или к требованию снижения операторских нагрузок, сокращения перечня допустимых конструкционных материалов, снижения длительности автономной эксплуатации объекта, т. е. в целом приводит к получению неадекватной оценки качества объекта контроля.

Вместе с тем проработанные концепции и методы, явным образом ориентированные на целевые установки и критерии диагностического контроля, которые формируются экспертами и нацелены на определенные уровни эффективности функционирования объекта (или системы), отсутствуют [8, 13-16]. Необходимость выработки нового методического подхода к оптимизации контроля особенно остро ощущалась в прикладных задачах экологического и радиационного мониторинга, где в силу несовершенства технологии переработки и использования радиоактивных материалов использовалась целая иерархия нормативных предельно-допустимых концентраций и уровней (ПДК и ПДУ) [17-18].

Предлагаемое методическое построение основывается на исследованиях и служит развитием более ранних работ, которые связаны с использованием концепции целевого контроля и первоначально близким образом трактовали понятие "функции параметр — свойство" [20, 21]. Оценку качества и эффективности контроля и выработку критериев оптимизации диагностического контроля предлагается основывать на новом подходе — введении некоторого критерия целевого контроля, на базе которого строится система показателей, обобщающая принципы допускового контроля.

ПОКАЗАТЕЛИ ДОСТОВЕРНОСТИ

Разработанный методический подход учитывает показатель эффективности, функционально описывающий уровень снижения вероятности выполнения предписанных задач или снижение работоспособности при отклонении контролируемого параметра от его нормативного значения. На этой основе получены оценки вероятностей гипер- и гиподиагностики (называемых иногда ошибками I и II рода). Может также вводиться функция риска, которая взвешивает средние ожидаемые ошибки с помощью весовых коэффициентов стоимости ущерба от ошибок каждого вида. Осуществляется оптимизация условий контроля путем выбора для НКП точности измерения и уровня контроля, которые соответствуют требуемым показателям достоверности и их относительному соотношению. Решение указанных задач включает построение аналитических соотношений и моделирование на ЭВМ.

В выражениях, определяющих ниже вероятности ложной и недостаточной диагностики, используются обозначения вероятностей: P ( ю 1 ; Q ₂) и P( to ₂; Q 1 ), где го 1 и го ₂ — состояние подсистемы (или объекта) адекватное и неадекватное задаче контроля; Q 1 и <Е — соответствующие решения о состоянии объекта. Таким образом, P ( to 1 ; Q ₂) отражает вероятность ложной диагностики (ВЛД), или гипердиагностики, а P( to ₂; Q 1) — вероятность недостаточной диагностики (ВНД), гиподиагностики. Соотношения включают вид распределения КП и погрешности его измерения, а также интервал ошибки измерения А = 2 а _{ош и б нк п}, рассчитанный на предельную погрешность измерения КП. Соотношения имеют вид:

^

P( to^ Q ₂) = ВЛД = J E ( x ) • f ( x ) • d x +

Q +А

Q +А

+ J E ( x ) • f ( x ) •

Q -А

А

J ф(5) • d5

Q -А

• d x ,

Q -А

P ( to ^Q 1 ) = ВНД = J [ 1 - E ( x ) ] f ( x ) • d x +

Q +А

+ J [1-E(x)]• f(x)•

Q -А

" Q -А

J

-А

ф (5) • dd • dx,

где Е ( х ) — ц елевой к ритерий к онтроля (ЦКК), или функция зависимости вероятности сохранения желаемого уровня функционирования от величины отклонения НКП от номинального значения; f ( x ) — плотность распределения центрированных значений НКП; ф ( 5 ) и А — плотность вероятностного распределения погрешности измерения НКП и интервал ее изменения.

Для модели распределения НКП использован класс экспоненциально-степенных распределений. Этот класс составляет семейство плотностей распределения различной формы, которые характеризуются тремя параметрами: математическим ожиданием m_x , среднеквадратичным отклонением a_x и параметром формы а

f ( x ) =

α

2 Ao _x ■ Г | ¹ | I a J

• exp

V

x — m x Ao _x

a A

где

^

^Г( P ) = J y^{p - 1} exp^{( -} y ) • ^d y

полная) гамма-функция.

Функция распределения

— обычная (т. е.

экспоненциально-

степенного закона имеет вид

а x - mx j

X(5x I1

x J-

F (x) = J expi Z )• Z a • dZ.

- 2 Г ¹ I

V a J

Параметром масштаба распределения служит ß = λσ х . Множитель λ выражается через параметр формы α в соответствии с соотношением

степенного закона показывает высокую эффективность и более совершенную форму статистического анализа [22–24], он не нашел пока отражения в статистических справочниках и известных монографиях [25–27]).

МЕТОДИЧЕСКАЯ И ИНСТРУМЕНТАЛЬНАЯ КОМПОНЕНТЫ ДОСТОВЕРНОСТИ

X =

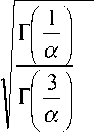
Некоторые типы экспоненциально-степенных распределений при различных значениях параметра формы α и m x = σ х = 1 представлены на рис. 1.

Широкое варьирование формы плотности распределений этого семейства позволяет получить от почти равномерного (при значениях α = 5,…, 8) до островершинного распределения (при α < 1.5) и включает в качестве частного случая (при α = 2) закон Гаусса, т. е. нормальное распределение. (Следует отметить: несмотря на то что использование метода на основе экспоненциально-

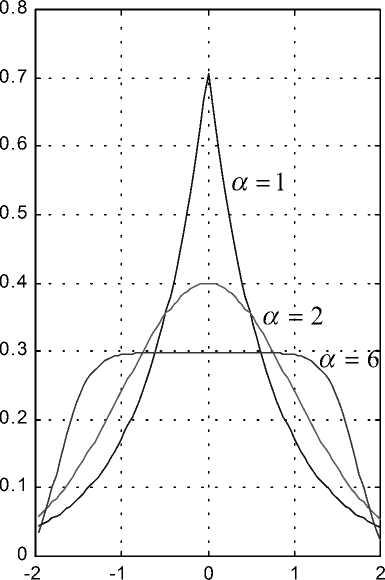
Рис. 1. Семейство экспоненциальностепенных распределений

В развернутых выражениях для вероятностей ВЛД и ВНД можно выделить приборноаппаратурную, или "инструментальную", компоненту, которая обусловлена неточностью измерения НКП (с σ ошиб..нкп ), и методическую компоненту, которая остается даже при абсолютно точном измерении НКП. Наличие методической компоненты Р мет .И; Q 2 ) и Р ме, ( « 2 ; Q 1 ) (или ВЛД мет. и ВНД мет. ) связано с построением ЦКК как функции, равной вероятности работоспособного состояния объекта или (в общем случае) с остояния, а декватного з адаче к онтроля (САЗК). Такой подход к построению ЦКК близок к принципу размытой логики, который состоит во введении функции принадлежности (вероятности) множеству, в нашем случае множеству САЗК.

Таким образом, в общих показателях достоверности контроля ВЛД и ВНД можно аналитически выделить ВЛД мет. и ВЛД инстр. (и аналогично ВНД инстр. и ВНД мет. ). Это разделение соответствует выражениям:

P «; Q 2) = Рмет. («; Q 2) + Ринстр. («1; Q 2),(6)

P («2; Q1)=Рмет. («2; Q1) + P («2; Q1),(7)

—

РметХ«1; Q 2) = J E (x) f (x)dx,(8)

Q

Q

Рмет.(«2; Q 1) = J!-E(x)]f(x)dx.(9)

-—

В рамках модели принятого экспоненциальностепенного распределения для КП методические компоненты показателей достоверности контроля в форме вероятностей ошибочных решений типа ВЛД и ВНД имеют вид:

Р мет. ( « 1 ; Q 2 ) =

—

J ^exp

Q

0.693 ^x

x ₀

a

( 1 A 2 X Г1 — o.

V 2 a J •

X

x

2 a

X exp -

x

72 x ° x

- d x ,

^Р мет. ( ^Ю 2 ; ^ 1 ) =

2а

х exp-

x

² ^

где X =

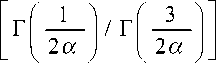
■ d x ,

Соотношения, определяющие Р _инстр ( « 1 ; Q ₂) и Р инстр ( ^ю 2 ; ^ 1 ), представляются выражениями значительно более сложной формы, поэтому достаточно использовать выражения (6) и (7) совместно с (1) и (2). Кроме того, следует отметить, что раскрытие сложного аналитического представления, сохраняющего, например, Г-функции, не дает значимого преимущества, т. к. программно осуществляется и прямое вычисление двойных интегралов.

Информационным обеспечением метода служит комплекс зависимостей и номограмм. В терминах целевого контроля, кроме показателей достоверности контроля, имеется возможность интерпретировать и такие обобщенные показатели, как средний уровень функционирования подсистемы, уровень гигиенического качества среды [28].

ЦЕЛЕВОЙ КРИТЕРИЙ

Целевой критерий должен быть на уровне единицы (100 % эффективности) при отсутствии отклонения НКП от нормативного значения (или от нулевого загрязнения — в случае мониторинга окружающей среды или радиационного контроля) и уменьшаться с различной скоростью при возникновении ухода НКП. В качестве наиболее подходящей (по принципу простоты и широких возможностей аппроксимаций) для ЦКК выбрана экспоненциальная зависимость вида exp[–0.693( x / x 0 ) ⁿ ], где x имеет значение текущего НКП, n является параметром формы ЦКК, а x 0 — параметр масштаба, который эквивалентен величине НКП, соответствующий снижению ЦКК в 2 раза.

Построение целевого критерия контроля связано с двумя этапами [19, 28]. Первый этап включает экспертное решение относительно того, какова степень снижения эффективности контролируемой

а

б

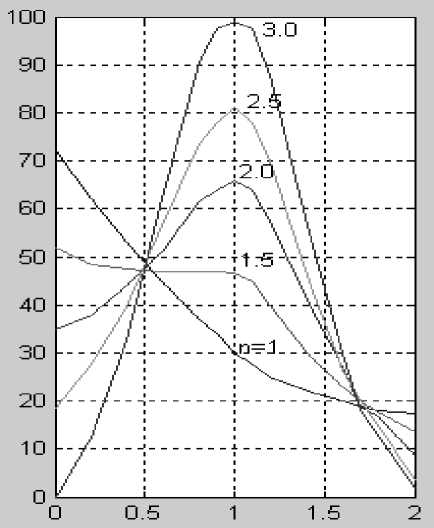
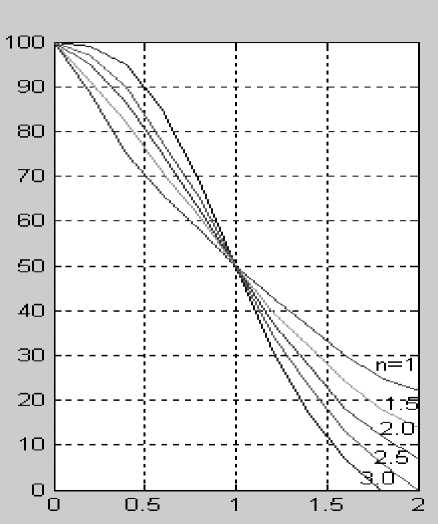
Рис. 2. Целевой критерий контроля (ЦКК, %) при различных значениях параметра формы ( n = =1; 1.5; 2; 2.5; 3) в зависимости от величины контролируемого параметра (по оси Х ), выраженного в единицах параметра масштаба ЦКК (а);

б — чувствительность критерия ЦКК (по оси Y ) к изменению величины НКП (по оси X ) при n = =1; 1.5; 2; 2.5; 3. Величина параметра n показана около кривых

подсистемы при различных отклонениях НКП от его нормального или специфицированного состояния. Этап содержит также задание реальной точности оценки НКП в процессе его контроля. Второй этап состоит в выборе параметра формы и масштаба ЦКК, которые обеспечивают аппроксимацию ЦКК. При этом оказывается удобным выбрать параметр масштаба (значения отклонения НКП, связанные со снижением эффективности на 50 %) совпадающим с аналогичным параметром экспертного ЦКК. В этом случае аналитический вид ЦКК, привязанный к экспертным оценкам ЦКК в двух точках — 100 % и 50 % эффективности, — легко адаптируется к требуемой зависимости с помощью простого подбора параметра формы n .

Вид ЦКК для различных значений параметра формы (n = 1,…, 3) и для масштабного параметра (x0), равного единице, показан на рис. 2, а вместе с кривыми чувствительности этого критерия к изменению величины НКП (рис. 2, б). Чувствительность определяется как модуль производной ЦКК d E (x) d x

x = НКП

и обычно имеет максимальное значение для случая, когда НКП равно величине масштабного параметра ЦКК (x0).

Найденные значения параметров ЦКК в дальнейшем служат входом в расчетные зависимости показателей достоверности, которые имеются в графической форме или реализуются программно.

а

КОМПОНЕНТЫ ПОКАЗАТЕЛЕЙ ДОСТОВЕРНОСТИ

Методическую компоненту показателей достоверности нельзя устранить или снизить простым увеличением точности приборно-аппаратурного (инструментального) контроля параметра, т. к. она является только отражением вероятностного распределения НКП, которое присутствует даже без дрейфа за пределы интервала ошибки измерения. Так что улучшение показателей достоверности связано с инструментальной компонентой.

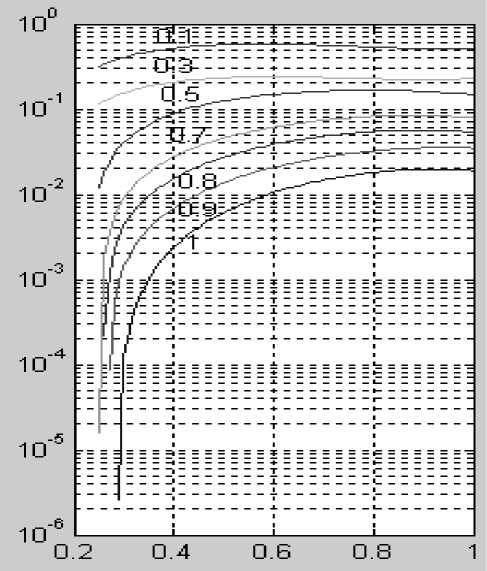
Зависимость методической компоненты достоверности контроля (вероятности ложной диагностики ВЛД_мет. и вероятности недостаточной диагностики ВНД мет. ) показаны на рис. 3.

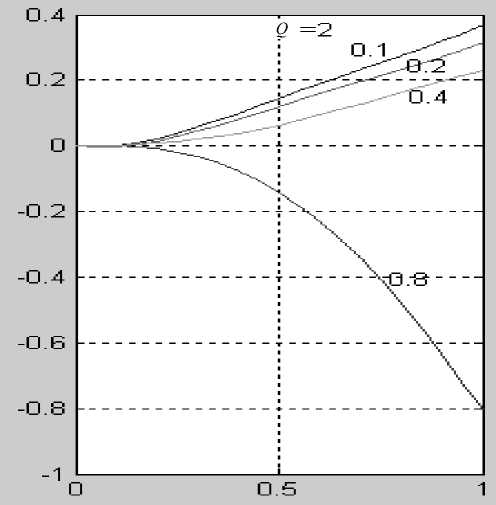
Особое значение в повышении показателей достоверности контроля имеет инструментальная компонента и доля ее в общих показателях (рис. 4).

Повышение точности измерения НКП действительно снижает величину вероятностей ошибочных решений. Однако это происходит до тех пор, пока инструментальная компонента не становится существенно меньше методической компоненты. Когда это происходит, улучшение показателей

б

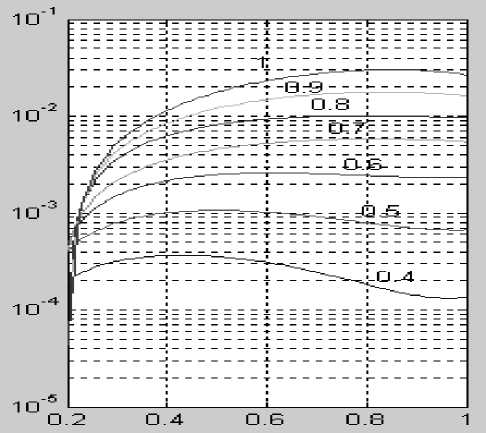
Рис.3. Зависимость методической компоненты показателей достоверности контроля (вероятности ложной диагностики и вероятности недостаточной диагностики) от величины среднеквадратичного рассеяния КП и уровня контроля КП. Уровень контроля в единицах масштабного параметра ЦКК указан на кривых. Среднеквадратичное рассеяние НКП в тех же единицах указано на оси Х . Зависимости построены для ЦКК с параметром формы n = 5 и гауссова (нормального) распределения КП. По оси Y показаны: а — вероятность ложной диагностики (ВЛД_мет.); б — вероятность недостаточной диагностики (ВНД мет. )

а

достоверности резко замедляется и цена улучшения показателей за счет повышения точности становится слишком высокой. Несоблюдение этого правила может привести (и иногда приводило) к неоправданно высоким требованиям к инструментальному контролю. В случае чисто допуско-вого контроля это, как следствие, приводило к недостаточно обоснованно высокой доле объектов, направляемых на обслуживание, к сокращению периода тренажа оператора по данным медикофизиологического контроля или к дорогостоящим операциям по снижению уровней загрязнения на сложных участках технологии.

Если для краткости обозначить показатели достоверности (временно без различения на ВЛД и ВНД) через Р , а полную величину показателя — через Р рез. , то имеет место соотношение

р р инстр. + рмет _ 1

Р рез.

Р рез.

Поэтому, предполагая известными значения

б

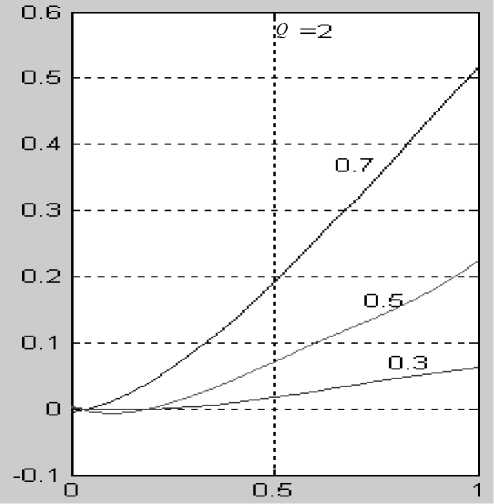
Рис. 4. Доля ( η ) инструментальной (приборноаппаратурной) компоненты в результирующих вероятностях ошибочных решений о состоянии объекта контроля при различном уровне Q контроля КП и ошибке измерения КП. Значения Q в единицах масштаба ЦКК указаны около кривых. Величина интервала Δ ошибки измерения КП (на оси Х ) дана в единицах уровня контроля КП (Δ / Q ).

а — по оси Y вероятности недостаточной диагностики η 21 = Р инстр. ( ω 2 ;Ω 1 ) / Р рез. ( ω 2 ;Ω 1 ). б — по оси Y вероятности ложной диагностики η 12 = = Р инстр. ( ω 1 ;Ω 2 ) / Р рез. ( ω 1 ;Ω 2 )

П ^_

р рез.

р инстр.

р рез.

мет.

1 - п

, можно с помощью (12) получить

, не используя при этом специаль-

ных графических зависимостей.

Величина отношения инструментальной и методической компонент достоверности

ВЛД инстр. / ВЛД мет. и ВНД инстр. / ВНД мет.

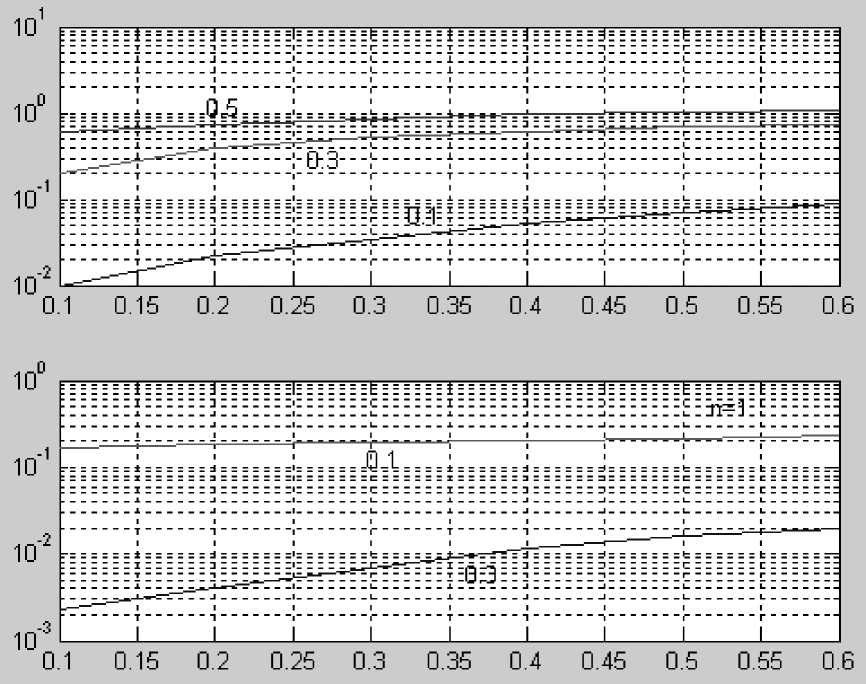
в зависимости от интервала ошибки измерения НКП показана на рис. 5, где параметром у кривых дано значение уровня контроля в единицах параметра масштаба ЦКК.

ПРИМЕРЫ ПРИМЕНЕНИЯ

Описанный метод построения показателей достоверности контроля по целевому критерию естественным образом адаптируется к области медикотехнических исследований, в частности при подготовке специалистов (операторов — по терминологии эргономики) для длительного, автономного обеспечения технических объектов, таких как водолазные полунатурные стендовые комплексы, транспортные глубоководные аппараты с новой энергетикой, отдельные объекты аэрокосмической техники. В области исследований, связанных с этими направлениями, при использовании полу-натурных тренажеров необходим медикофизиологический контроль человека в субэкстремальных условиях. При этом имеют своеобразную специфику критерии, определяющие относительную эффективность состояния таких подсистем

а

б

Рис. 5. Отношение (а) приборно-аппаратурной (инструментальной) компоненты вероятности ложной диагностики (ВЛД_инстр.) к методической компоненте этой вероятности (ВЛД_мет.) при различных параметрах системы контроля: интервале Δ ошибки измерения НКП (на оси Х ) и уровне контроля НКП в единицах σ _нкп. Значения УК_нкп = 0.1; 0.3; 0.5 указаны на кривых. Представленные зависимости соответствуют σ _нкп = 0.1.

б — зависимость вероятности отношения ВНД_мет. к ВНД_инстр. от Δ при различных значениях уровня контроля: УК нкп = 0.1; 0.3 (указаны на кривых). В расчетах использован целевой критерий ЦКК с параметром формы n = 1

организма как система дыхания и сердечная деятельность. Исходными данными для контроля и, следовательно, для выработки ЦКК служит частота дыхания и частота сердечных сокращений, субэкстремальные нагрузки (физические, оперативно-тактические, температурные, гипербарические и др.). При контроле такие данные с учетом длительности тренажа и опыта проводившихся ранее экспериментов используются для выработки экспертных решений о характере и форме ЦКК.

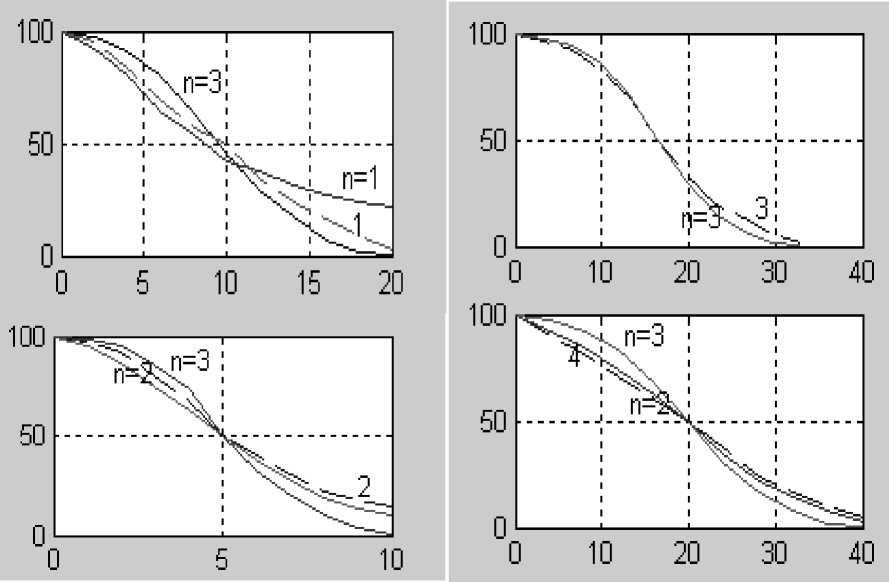
Некоторые из таких критериев и значения соответствующих параметров формы для апробации различных вариантов экспертных критериев контроля показаны на рис. 6.

Другим примером возможного использования метода ЦКК может служить область радиационного контроля, где набор требований к точности измерения дозы (а чаще ее косвенной оценки) обусловлен формой целевого критерия контроля, в качестве которого принимается зависимость вероятности отсутствия радиационного повреждения от величины дозы (рис. 7). Эти кривые по сути являются зеркальным отражением экспериментально установленных зависимостей поражающего эффекта от дозы.

ЗАКЛЮЧЕНИЕ

Таким образом, разработан метод контроля определяющего параметра подсистемы (или объекта),

а

б

в

г

Рис. 6. Виды целевого критерия контроля по частоте дыхания (ЧД, мин^–1 — а, б) и частоте сердечных сокращений (ЧСС, мин^–1 — в, г) для условий контроля оператора при различных условиях профессиональной нагрузки или при длительной дозированной физической нагрузке. Пунктирные кривые (они пронумерованы цифрами 1–4) построены по данным экспертных критериев контроля, полученных по оценке снижения уровня функционирования контролируемой физиологической системы. Расчетные значения ЦКК (при n = 1, n = 2 и n = 3), аппроксимирующего экспертные критерии, даны сплошными кривыми.

а — расчетный ЦКК при n = 1и n = 3 для 1-го варианта экспертного ЦКК по ЧД (по оси Х дано отклонение ∆ЧД от нормального значения ЧД, мин^–1); б — аппроксимация 2-го варианта экспертного критерия контроля по ЧД при n = 2 и n = 3; в — сравнение расчетного ЦКК при n = 3 с экспертным критерием контроля оператора по ЧСС (по оси Х — ΔЧСС, мин^–1); г — аппроксимация другого экспертного критерия контроля (вариант 4) с помощью расчетного ЦКК при n = 2 и n = 3

отличающийся тем, что он базируется на формировании целевой концепции контроля, — на так называемом целевом критерии контроля (ЦКК). ЦКК является функцией, представляющей вероятность работоспособного состояния подсистемы при различных значениях НКП, и имеет вид exp[–0.693|∙x / x0|n], где n и x0 — параметры формы и масштаба ЦКК (х = НКП). Выбор значений параметров в ЦКК делает возможным, чтобы критерий аппроксимировал ЦКК (как вероятность состояния, адекватного задаче контроля при различной величине НКП), определенный экспертами исходя из общей концепции качества функционирования под- системы при отклонении НКП от оптимального (специфицированного) значения. Дополнительно задается некоторое значение уровня контроля.

В качестве п оказателей д остоверности (ПД) приняты вероятности ошибочных решений о работоспособном состоянии контролируемой подсистемы. ПД (аналогично ошибкам I и II рода в теории принятия решений) относятся к двум видам: к вероятности недостаточной диагностики ВНД ("плохое" состояние ω 2 подсистемы и "хорошее" решение Ω 1 о ней) и к вероятности ложной диагностики ВЛД ("хорошее" состояние ω 1 системы и решение Ω 2 о том, что состояние "плохое").

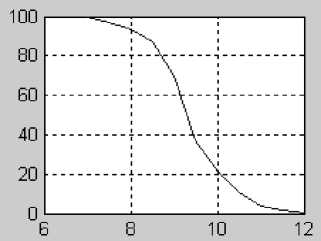
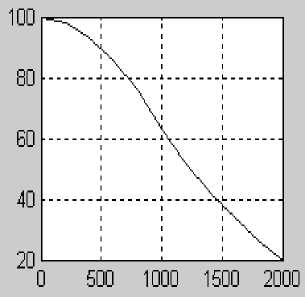
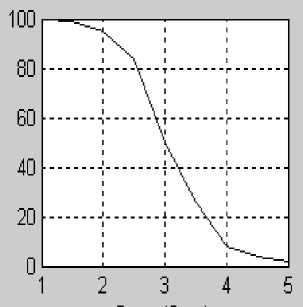
Рис. 7. Целевой критерий контроля в форме вероятности отсутствия радиационного повреждения после воздействия различных доз на органы человека (доза в единицах грей — по оси X ).

а — модель ЦКК как вероятность отсутствия возникновения пневмонийных участков дыхательных путей при облучении; б — ЦКК как вероятность отсутствия поражения щитовидной железы при инкорпорации радиоактивного иода-131; в — вероятность отсутствия индуцированной облучением катаракты как модель ЦКК

Полученные показатели достоверности контроля зависят от ЦКК, плотностей распределения НКП и погрешности его измерения и от уровня контроля. В аналитическом выражении ПД для распределения НКП предусмотрен э кспоненциально- с тепенной з акон (ЭСЗ), для которого распределение Гаусса (нормальное) является частным случаем при значении параметра формы α = 2 в ЭСЗ. ПД получаются с помощью расчетных графиков или программно.

В ПД выделены методическая и инструментальная компоненты и определен их вклад в общие ПД (в вероятности ложной и недостаточной диагностики). Методическая компонента дает достижимый предел величины ПД при точном измерении КП. Решение "обратной задачи" позволяет исходя из задания ЦКК по требуемой величине ПД находить приемлемые уровни контроля и необходимую точность измерения КП.

Представлены примеры ЦКК для задач медикотехнического контроля: контроля частоты сердечных сокращений у операторов в условиях тренажера и ЦКК для радиационного контроля по схеме "доза облучения — уровень биологического повреждения".