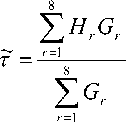Система прогнозирования длительности ожидания подтверждений в телекоммуникационной сети
Автор: Польщиков Константин Александрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 2 т.13, 2015 года.
Бесплатный доступ
Статья посвящена разработке системы, предназначенной для прогнозирования длительности ожидания подтверждений в телекоммуникационной сети. Система базируется на применении четырехслойной нейронной сети, функционирующей на основе нечетких правил. Представлена функциональная схема системы, сформированы обучающие данные, полученные путем измерения длительности ожидания подтверждений на пакеты заданного потока данных в реальной телекоммуникационной сети. Предложенная система предназначена для оценки загруженности телекоммуникационной сети, а также для управления интенсивностью отправки данных и повторных передач.
Нейро-нечеткая система, длительность ожидания подтверждений, прогнозирование, телекоммуникационная сеть
Короткий адрес: https://sciup.org/140191755
IDR: 140191755 | УДК: 621.396.9 | DOI: 10.18469/ikt.2015.13.2.06
Текст научной статьи Система прогнозирования длительности ожидания подтверждений в телекоммуникационной сети
В телекоммуникационных сетях с коммутацией пакетов для обеспечения достоверной доставки информации применяется квитирование, то есть передача подтверждений (квитанций) на пакеты данных, которые были успешно доставлены адресату [1]. Длительность ожидания этих подтверждений является важным параметром, значения которого характеризуют загруженность сети, а результаты их прогнозирования могут быть использованы для управления интенсивностью отправки данных и повторных передач [2–7].
Анализ литературы показал, что вопросам получения качественного прогноза этой величины уделяется мало внимания. Поэтому разработка системы, предназначенной для прогнозирования длительности ожидания подтверждений в телекоммуникационной сети, является актуальной научно-технической задачей.
Синтез системы
Успешно осуществлять экстраполяцию тех или иных случайных функций позволяет применение нейро-нечеткой системы, сочетающей в себе преимущества нечеткой логики и искусственной нейронной сети [8-13].
Синтезируемая нечеткая нейронная сеть предназначена для определения величины – прогнозируемой длительности ожидания подтверждения на пакет, отправляемый источником данных. На вход разрабатываемой системы подаются величины то есть значения длительности ожидания подтверждений на три предыдущих пакета, отправленных источником данных.
Исследования показали, что достаточную точность прогнозирования длительности ожидания подтверждения обеспечивает применение нечеткой нейронной сети со следующими параметрами: алгоритм нечеткого вывода – Суге-но нулевого порядка [14], количество функций принадлежности для каждой входной величины – две, форма функций принадлежности для каждой входной величины – треугольная, алгоритм обучения нейронов – обратного распространения ошибки [15-16].
Функционирование синтезируемой системы основано на применении базы нечетких правил следующего вида:
Если (гт = X,) и (tv = У,) и (т, = Z,), то (т = НХ), Если (тх = Xx^u^cv = У]) и (г, = Z2),то (г = Я2), Если (тх = Xx)u(tv = Y2)u(t_ = Zx),то (г = Я3), Если (гv = Хх) и (гv = У) и (г_ = Z2), то (г =Н4), Если (rr = Jf2)w(rr =¥х)и(т. =Zx\mo (т =Н5),
Если Yx = Хг) и (г = Yj) и (г. = Z2\ mo (г = Я6),
Если (гv = Х2)и(т = У2)и(т. = Zv),mo (т =Н7У
Если (гх = Х2)г/(гг = У2)г/ (г, = Z2\mo (т =Н^, где ^ – терм №1 входной величины Тх ; – терм №2 входной величины гх ; Z1 – терм №1 входной величины Tv ’ Z2 – терм №2 входной величины 5- Z1 – терм №1 входной величины Tz; Z2 – терм №2 входной величиныc:; HV,H2, Я8 – значения индивидуальных выводов нечетких правил. Вид и параметры функций принадлежности для каждой входной величины показаны на рис. 1-3.
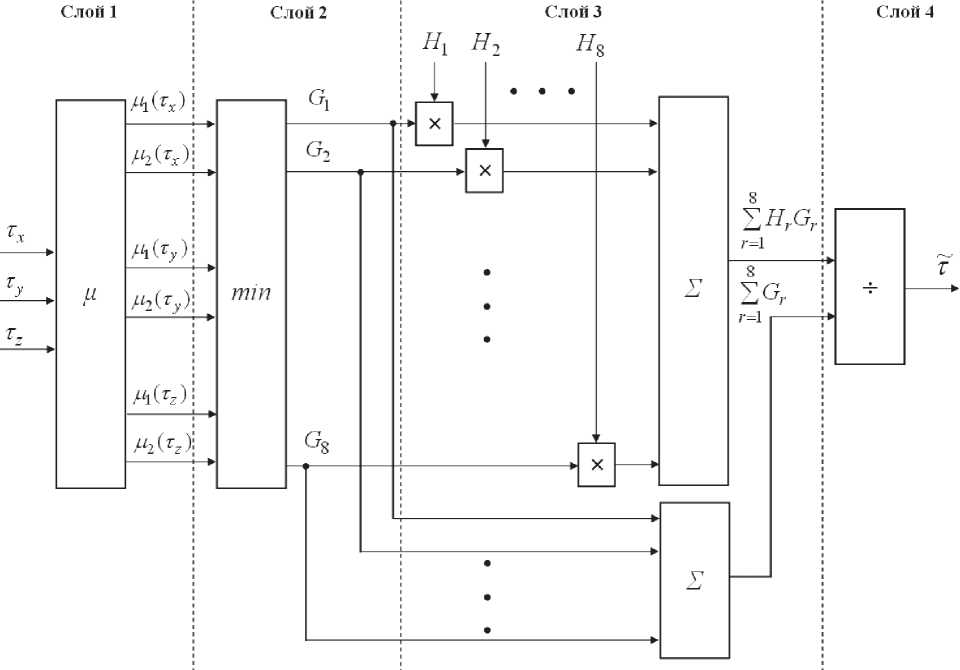
Система прогнозирования длительности ожидания подтверждений состоит из четырех ней ронных слоев (рис. 4).
С помощью первого слоя нейронов выполняется процедура фаззификации, то есть вычисляются значения функций принадлежности для каждой входной величины:
|
Tx < ^.vl ’ |
||
|
M\Vt^ = ^ |
bxX-^x |
aX\ - Tx < bx\ |
|
bx\ ~ax\ |
||
|
o, |
Tx^bxv, |
Tx < ax2‘->
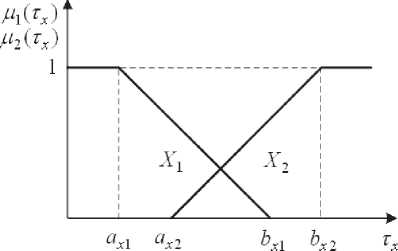
Рис. 1. Вид и параметры функций принадлежности для величины Tx
MyW^
X - ax2
Ьх2 "^2
«Xi ^ Tx x2;
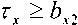
ayl - Ty < byl ’
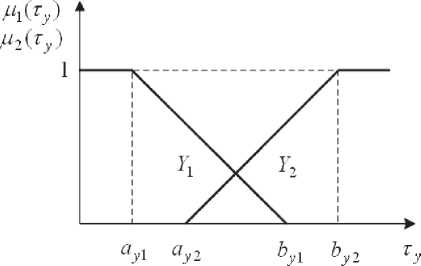
Рис. 2. Вид и параметры функций принадлежности для величины T -y
MTz^*
bz\ ~ ^z b._x-a„_V
azY^z Рис. 3. Вид и параметры функций принадлежности для величины T- Вторым слоем нейронов осуществляется процедура агрегирования, в результате которой определяется степень истинности каждого нечеткого правила: G\ = M\ ^x)л Р\ У у Vm^t.y, Gy = Ц\ Yx ) Л M\ (Гу ) A A2 <^z ) ; Gy = ^Tx) AjUyYY A^(r.); G4 = Mx Yx ) Л ц2 Yx ) Л ц2 Yz ); G5 = /А (A-) л Ц\ <ту) A ^ (r_); Gb = /А (а)л Al ( A’) A ^2 (г, ) ; G1 = A2 ( Ay ) л A2 ( A' ) A //! (Г- ) ; Параметр «И ах2 ЬХ\ Ьх2 ау1 ау2 Значение 3,75 26,74 3,63 28,3 3,75 27,57 Параметр Йу1 Ьу2 «Z1 az2 bzl bz2 Значение 3,535 27,87 3,594 27,87 3,508 27,9 При получении матрицы (1) в течение 7 = 750 циклов наблюдения в реальной телекоммуникационной сети осуществлялось измерение длительности ожидания подтверждений на пакеты заданного потока данных. Настройка нейро-нечеткой системы проводилась в программной среде Matlab с использованием 8 циклов обучения. В таблице 1 представлены результаты обучения нейронов первого слоя, а в таблице 2 содержатся результаты обучения нейронов третьего слоя. Таблица 2. Результаты обучения нейронов третьего слоя Параметр Нх н. Н3 я4 Значение 3,837 -6,012 7,257 8,733 Параметр н5 н6 Я7 я8 Значение 31,48 20,88 27,89 26,36 В результате проведения в программной среде Matlab многочисленных имитационных экспериментов установлено, что точность определения величины т с помощью синтезированной нейро-нечеткой системы находится в пределах 96,2 … 98,1%. Заключение Таким образом, синтезирована нейро-нечеткая система, предназначенная для прогнозирования длительности ожидания подтверждений на пакеты данных. Система состоит из четырех нейронных слоев, выполняющих процедуры нечеткого вывода (фаззификацию, агрегирование, активизацию и дефаззификацию). Для настройки весов нейронов используются обучающие данные, отражающие динамику изменения длительности ожидания подтверждений в реальной телекоммуникационной сети. Предложенная система может быть использована для оценки загруженности сети, а также для управления интенсивностью отправки данных и повторных передач.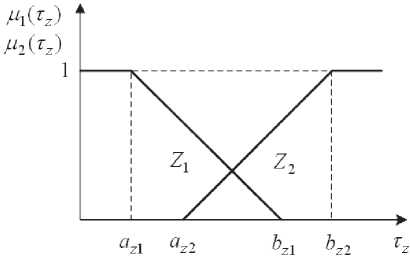
Список литературы Система прогнозирования длительности ожидания подтверждений в телекоммуникационной сети
- Postel J. Transmission control protocol. RFC 793//http://www.faqs.org/rfcs/rfc793.html.
- Paxton V., Allman M. Computing TCP’s Retransmission Timer. RFC 2988//http://www.rfc-editor.org/rfc/rfc2988.txt
- Polschykov K., Kubrakova K., Odaruschenko O. Methods аnd Technologies Analysis of The Real-Time Traffic Transmission Requests Servicing//World Applied Programming. Vol. 3, Issue 9, 2013. -P. 446-450.
- Рвачева Н.В., Польщиков К.А., Волошко С.В. Метод выбора межсегментного интервала в транспортном протоколе телекоммуникационной сети//Проблемы телекоммуникаций. № 2 (4), 2011. -С. 72-82.
- Польщиков К. А. Метод нейро-нечеткого управления интенсивностью повторных передач в телекоммуникационной сети//Информационные технологии и телекоммуникации. Вып. 2, 2013. -С. 32-41.
- Polshchykov K. O. Synthesis of neuro-fuzzy systems of data flows intensity control in mobile ad-hoc network//Microwave and Telecommunication Technology (CriMiCo), 23rd International Crimean Conference, 2013. -P. 517-518.
- Польщиков К. А. Метод нейро-нечеткого управления интенсивностью отправки данных узлами-источниками в мобильной радиосети специального назначения//Наука i технiка повiтряних сил Збройних Сил України. № 3 (9), 2012. -С. 118-122.
- Леоненков А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. СПб: БХВ-Петербург, 2003. -736 с.
- Усков А. А., Кузьмин А. В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. М.: Горячая линия -Телеком, 2004. -143 с.
- Польщиков К. А. Обобщенные модели нейро-нечетких систем управления интенсивностью потоков данных в мобильной радиосети//Science and Education a New Dimension. Vol. 8, 2013. -P. 133-137.
- Польщиков К. А., Здоренко Ю. Н. Усовершенствованный метод нейро-нечеткого управления отбрасыванием пакетов в транзитных маршрутизаторах телекоммуникационной сети//Проблемы телекоммуникаций. № 2 (14), 2014. -С. 76-90.
- Польщиков К.А., Кубракова Е.Н., Краснобаев В.А. Модель нейро-нечеткого прогнозирования средней интенсивности поступления запросов на передачу потоков реального времени по каналу телекоммуникационной сети//Системи обробки iнформацiї. № 2 (118), 2014. -С. 193-197.
- Польщиков К.А., Здоренко Ю.Н., Сокол Г.В. Методика нейро-нечеткого прогнозирования потерь пакетов при перегрузке компьютерной сети//Научный вестник ДГМА. №2 (8Е), 2011. -С. 77-86.
- Takagi Т., Sugeno М. Fuzzy identification of systems and its applications to modeling and control//IEEE Transactions on Systems, Man, and Cybernetics. Vol.15, No 1, 1985. -Р. 116-132.
- Rumelhart D. E., Hinton G. E., Williams R. J. Learning Internal Representations by Error Propagation//Parallel Distributed Processing. -Cambridge: MIT Press. V.1, 1986. -P. 318-362.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. М.: Горячая линия -Телеком, 2006. -452 с.