Система управления роботом-манипулятором с использованием нейросетевых алгоритмов ограничения рабочей области схвата

В 2015 году филиалом Южно-Уральского государственного университета в г. Миассе по техническому заданию одного из ведущих предприятий атомной промышленности был спроектирован и изготовлен робототехнический комплекс МР-48. Его основное назначение – исключение ручных операций и введение автоматизированных и автоматических режимов работы при выполнении технологических операций с материалами в условиях сильных радиационных полей. Манипулятор робототехнического комплекса МР-48 конструктивно представляет собой шестизвенный манипулятор с вращательными степенями свободы в каждом сочленении. Кинематическая схема манипулятора, а также системы координат, связанные с каждым из звеньев, заданные в соответствии с правилами Денавита – Хартенберга [1], представлены на рис. 1, 2.

Рис. 1. Кинематическая cхема манипулятора МР-48

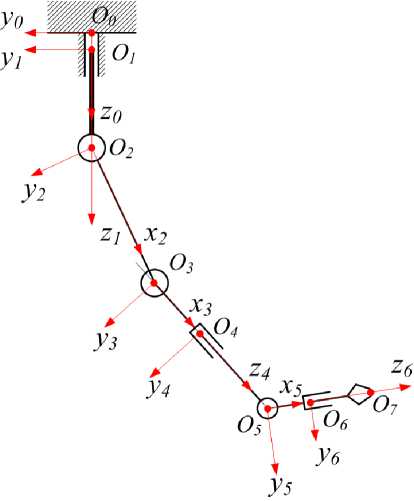
Рис. 2. Оси систем координат, связанные со звеньями

Управление в технических системах

Параметры кинематики манипулятора в представлении Денавита – Хартенберга приведены в таблице.

Параметры системы координат звеньев манипулятора

i	Сдвиг θ i , °	α i , °	a i , м	d i , м	Диапазон, °
1	0	90	0	0,14	+176…–251
2	90	0	0,39	0	±109
3	90	90	0,02	0	±95
4	180	90	0	0,32	±194
5	180	90	0,02	0	±109
6	0	0	0	0,35	±360

В состав аппаратуры роботизированного комплекса МР-48 входит, помимо манипулятора, пульт оператора с ЭВМ и органами управления, источники питания, усилительно-преобразующие модули, соединительные кабели. Структурная схема робототехнического комплекса представлена на рис. 3. Внешний вид манипулятора МР-48 и его пульта управления представлен на рис. 4, 5.

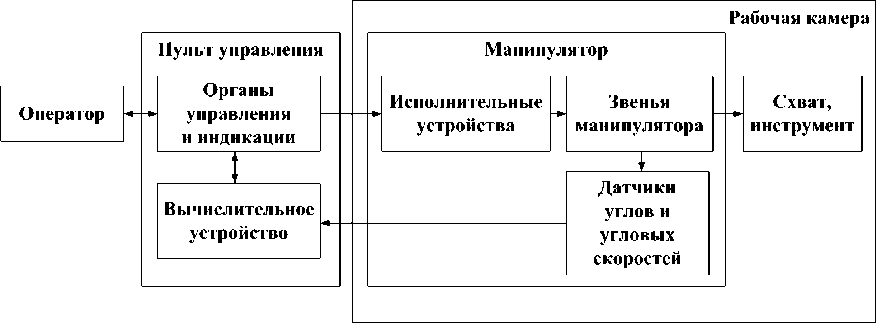
Рис. 3. Структурная схема робототехнического комплекса МР-48

Рис. 4. Внешний вид манипулятора МР-48

Рис. 5. Внешний вид пульта управления

Описание системы управления

Ядром системы управления (СУ) является ЭВМ пульта оператора, сопряженная с органами управления, датчиками и исполнительными устройствами посредством модулей ввода-вывода, также являющимися аппаратно-программными компонентами системы управления.

Входными и промежуточными сигналами системы управления манипулятора являются:

• 1.    Воздействия оператора на органы управления M i ;

• 2.    Мгновенные углы поворота (ориентации) звеньев q i ;

• 3.    Мгновенные угловые скорости поворота звеньев ω _i ;

• 4.    Требуемые значения углов и угловых скоростей q i уст , ω i уст , формируемые в контурах системы управления.

Выходными сигналами системы управления являются токи I i ( i = 1…6, т. е. для каждого исполнительного электродвигателя в составе звена), формируемые в каждый момент времени таким образом, чтобы манипулятор осуществлял требуемый характер движения.

В целом система управления является дискретной, с периодом формирования управляющих воздействий 20 мс. В силу специфики объекта управления (манипулятора) и режимов его работы СУ реализована в виде нескольких вложенных контуров управления, реализованных на аппаратном, аппаратно-программном либо программном уровнях.

Функциональная схема системы управления представлена на рис. 6.

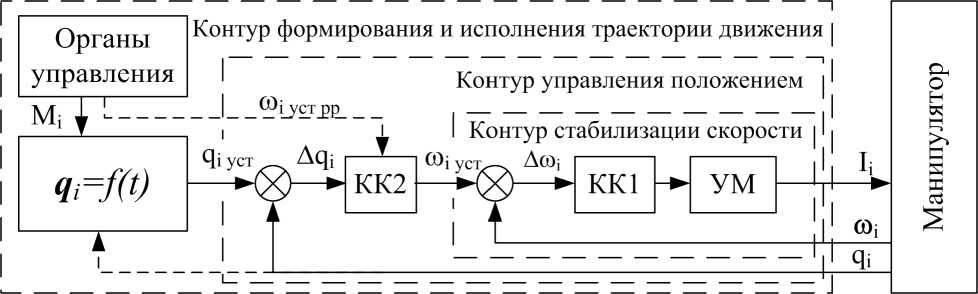
Рис. 6. Функциональная схема системы управления манипулятора

На функциональной схеме обозначены:

• КК 1 – корректирующий контур (регулятор) стабилизации скорости вращения звеньев манипулятора;

• УМ    – усилитель мощности, преобразующий широтно-модулированые сигналы управления в выходной ток исполнительных органов манипулятора;

• КК 2 – корректирующий контур (регулятор) положения звеньев манипулятора;

• q_i    – мгновенные углы ориентации звеньев манипулятора;

• ω i    – мгновенные угловые скорости поворота звеньев манипулятора;

• I i    – токи в исполнительных электродвигателях манипулятора;

Следует отметить, что управление манипулятором осуществляется в одном из трех основных режимов:

• 1.    Режим ручного управления, при котором оператор с помощью отклонения двух многоосевых джойстиков от нейтрального положения задает уставки скоростей поворота звеньев манипулятора ω _{i уст рр} , контролируя конфигурацию манипулятора визуально либо по показаниям датчиков углов на пульте управления;

• 2.    Режим управления в заданной системе координат, при котором оператор с помощью отклонения двух многоосевых джойстиков задает линейную скорость и направление движения точки схвата манипулятора ( О 7 , рис. 2).

• 3.    Режим формирования и последующего автоматического воспроизведения траектории движения манипулятора. В режиме воспроизведения траектории система управления автоматически формирует новые векторы углов ориентации звеньев в зависимости от времени q i уст = f ( t ) .

Типовым местом установки манипулятора при его эксплуатации является потолок герметичной защищенной рабочей камеры с вертикальным исходным положением МР-48, при этом, в за-

Управление в технических системах

висимости от типа рабочей камеры и ее линейных размеров, возможно частичное превышение рабочего пространства манипулятора над рабочей зоной камеры.

В ходе испытаний и опытной эксплуатации манипулятора, проводимых в течении 2016 года на предприятии заказчика, были выявлены случаи касания и ударов схвата манипулятора о стенки и внутренние элементы камеры, что может привести к возможным механическим повреждениям внутрикамерного оборудования и собственно манипулятора. В связи с этим был предложен вариант усовершенствования системы управления путем ввода дополнительного контура контроля нахождения схвата манипулятора в безопасной рабочей области (рис. 7).

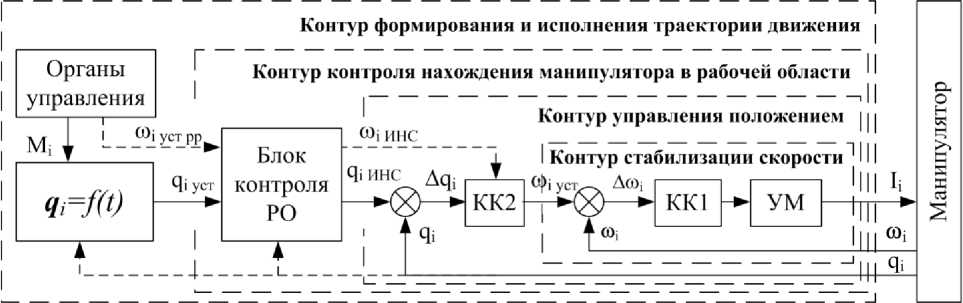
Рис. 7. Функциональная схема системы управления с контуром контроля рабочей области

Блок контроля рабочей области на основе информации о параметрах движения манипулятора с использованием классических методов решения прямой кинематической задачи вычисляет линейные координаты схвата манипулятора и далее сравнивает их с подпространством допустимых либо недопустимых координат (в простейшем варианте – из заранее сформированных массивов допустимых положений), формируя при этом необходимый набор выходных сигналов, используемых для коррекции или полной блокировки движения манипулятора.

В общем случае безопасная рабочая область (БРО) может иметь достаточно сложную конфигурацию и соответственно сложное геометрическое описание. Для составления такого описания зачастую требуются большие временные затраты высококвалифицированного персонала.

Одним из возможных путей решения задачи является применение искусственных нейронных сетей (ИНС) для задания БРО и контроля за выходом схвата манипулятора из нее. Как известно, ИНС обладает хорошими классификационными характеристиками, что можно использовать для выделения БРО из общего объема камеры [2]. Данный способ не требует предварительного геометрического описания БРО, так как оно автоматически формируется в процессе обучения (как на этапе начального обучения ИНС, так и в ходе эксплуатации при переобучении). Кроме того, нейросетевой алгоритм обладает высокой численной эффективностью, что немаловажно с учетом его встраивания в контур системы управления.

С целью проверки возможности использования ИНС для контроля выхода за границы БРО проведено компьютерное моделирование системы управления. С учетом того, что имеющееся управляющее программное обеспечение (ПО) разработано в системе NI LabView, для моделирования также использовалась данная среда. Дополнительно использованы программные пакеты расширения среды разработки NI Robotics (моделирование кинематики и динамики движения манипуляторов) и NI Super Simple Neural Networks (работа с ИНС).

В общем виде модель функционирования ИНС описывается выражением

Y = F^w^) = F(5) = F(WX^T),                                     (1)

где W = (w₁, w₂,..., w_n ) - вектор весовых коэффициентов;

X = (x₁, x₂,..., x_n) - вектор входных сигналов;

• 5 = Е ” ₌₁ W j X j - взвешенная сумма;

• F - оператор нелинейного преобразования или функция активации.

Сигмоидальная ИНС (персептрон) с одним скрытым слоем имеет структуру, представленную на рис. 8.

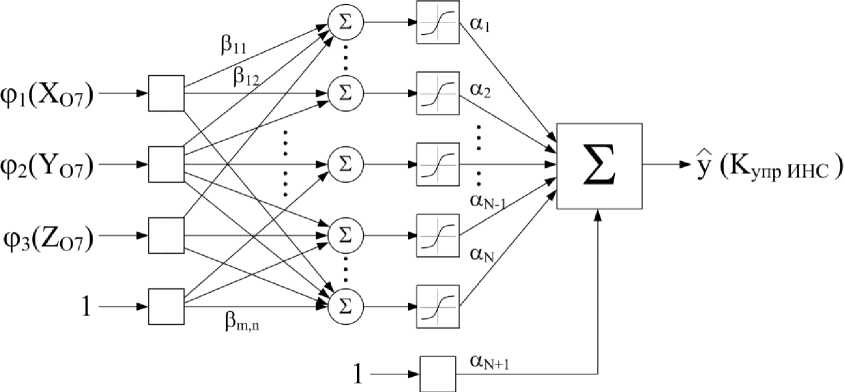
Рис. 8. Структура сигмоидальной ИНС с одним скрытым слоем

Выходное значение ИНС такого типа рассчитывается по формуле

• У ⁽ф, р, а) = S^ i а ; tanhQ^ i P i./ Ф у ) + а „+_ь                                          (2)

где N – количество нейронов в скрытом слое;

• n – количество входных данных (входной слой);

ϕ = [φ 1 , …, φ n , 1]^T – входной слой (исходные данные);

• β – матрица весовых коэффициентов;

• α – вектор весовых коэффициентов выходного слоя;

tanh – гиперболический тангенс.

В общем случае в персептроне может быть несколько скрытых слоев, тогда выход предыдущего слоя k

• Vp^tanh^+X-Vy)                                       (3)

рассматривается как вход скрытого слоя k + 1.

Входной слой ИНС формируется из текущих координат X , Y , Z схвата в базовой системе координат (точка O 7 на рис. 2). На выходном слое формируется значение K упр ИНС в диапазоне [0; 1], где 0 – выход за границы БРО, 1 – нахождение в пределах БРО. На данном этапе разделение областей производится по пороговому значению 0,5. При фиксации выхода за границы БРО коэффициент передачи положений органов управления резко снижается до некоторого минимального значения и оператору подается звуковой сигнал. Таким образом, ИНС выполняет роль контролера, но полностью не блокирует действия оператора, которому по-прежнему остается доступным весь объем камеры.

В процессе моделирования имитируется движение манипулятора по обучающей траектории, которая по возможности равномерно заполняет БРО. По ходу движения по обучающей траектории с тактом работы системы управления производится накопление массива данных о координатах X , Y , Z схвата (рис. 9).

Для формирования обучающего и проверочного набора данных полная рабочая область манипулятора покрывается сетью допустимых точек (в соответствии с его кинематической схемой и возможными углами поворота по осям) по методу Монте-Карло. Точкам, входящим в зону ε – трубки вокруг обучающей траектории, приписывается выходное значение 1 ( ε подбирается с таким расчетом, чтобы полностью «заполнить» БРО). К обучающему набору присоединяются также все точки обучающей траектории с выходным сигналом 1. Всем оставшимся точкам обучающего и проверочного набора приписывается выходное значение 0. Подмножество обучающего набора с выходом, равным 1 для объёма набора 10 000 точек и ε = 0,05, представлено на рис. 10.

Управление в технических системах

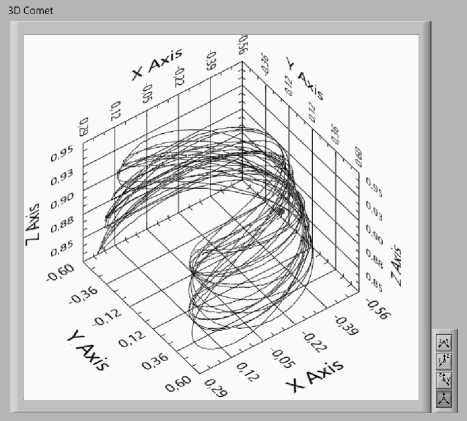
Рис. 9. Обучающая траектория

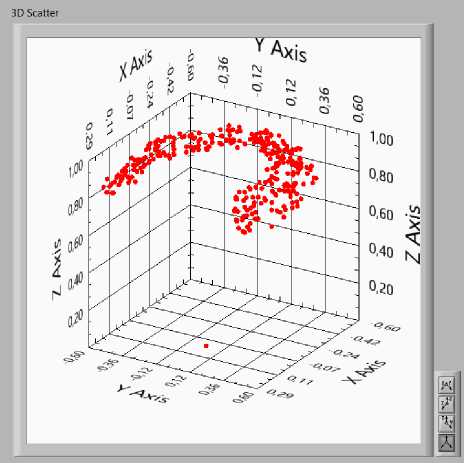
Рис. 10. Обучающий набор

Стандартным этапом работы с ИНС является этап обучения, в ходе которого ИНС настраивает матрицы весовых коэффициентов и другие внутренние переменные в соответствии с обучающим набором данных (известными векторами входных и выходных сигналов). Полный проход ИНС по всем векторам входных сигналов называется эпохой обучения. Цель обучения ИНС – последующее адекватное формирование выходного сигнала при эксплуатации ИНС с минимальным его отклонением от требуемого значения при любых возможных векторах входных сигналов. В пакете NI Super Simple Neural Networks настройка процесса обучения и этапы обучения представлены в виде диалогового окна в удобном для пользователя виде (рис. 11).

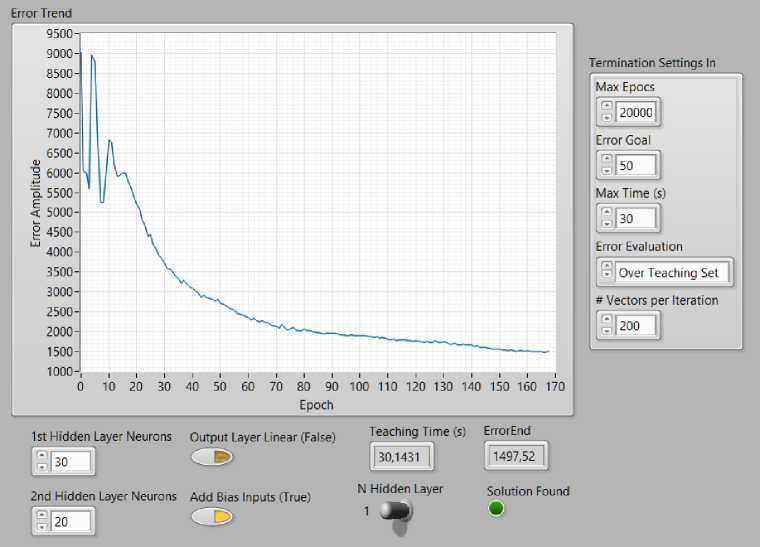
Рис. 11. Процесс обучения ИНС в пакете NI Super Simple Neural Networks

Обучение ИНС проводится путем минимизации среднеквадратической ошибки выхода методом градиентного спуска (алгоритм Левенберга – Марквардта)[3].

На рис. 12 приведено визуальное представление проверочного набора данных, на котором выполнялась верификация работы ИНС.

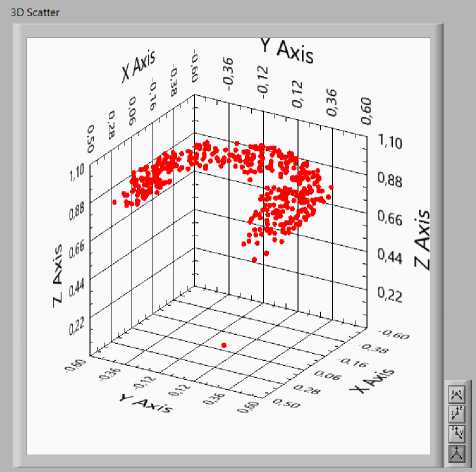
Рис. 12. Проверочный набор для верификации ИНС

Выводы

Проведенное моделирование СУ с контуром контроля положения схвата манипулятора подтверждает принципиальную пригодность использования ИНС для детектирования БРО достаточно сложной формы, для чего можно использовать однослойный либо двухслойный персептрон с 20–30 нейронами.

Аналогичным образом может быть реализована многоконтурная ИНС для контроля за положением промежуточных точек манипулятора (например, точек O ₃ , O ₅ ) с логическим объединением выходов независимых контуров контроля.

В целом по результатам математического моделирования принято решение о внедрении ИНС в рабочий образец робототехнического комплекса МР-48.