Система уравнений для определения функций распределения при вероятностных методах расчета

По действующим нормам [1, 2] и рекомендациям [3] прочность конструктивных систем и их элементов определяется сравнением внутренних усилий S_ext с их предельными значениями N_ult . Для вычисления S_ext и N_ult используются методы строительной механики и формулы несущей способности, в которых параметры конструктивных систем и их элементов считаются действительными числами.

В действительности все параметры являются случайными величинами, характеризующими случайные события, которые могут быть взаимосвязаны или независимы друг от друга.

В действующих нормах и рекомендациях случайность учитывается введением коэффициентов, полученных статистической обработкой экспериментальных данных. Можно предполагать, что при таком подходе возникают некоторые неточности, так как процесс вычисления есть моделирование естественных процессов с неустановленной степенью точности. В связи с этим возникли «вероятностные» методы расчета конструктивных систем [4, 5]. Эти методы основаны на применении определенных правил алгебраических операций над случайными числами (величинами) с учетом законов их распределения и допущений их взаимозависимости [6, 7, 8–10].

Задачами вероятностного метода расчета конструкций и сооружений является вычисление величин S_ext и N_ult путем математических операций над случайными величинами. При этом S_ext и N_ult будут являться случайными величинами или случайными процессами, характеризуемые функциями распределения, средними значениями, дисперсиями, стандартами.

Вопрос о надежности элемента конструкции и системы, решается сравнением Sext и Nult с заданной вероятностью отказов, при этом эти величины являются функциями случайных величин или случайными функциями.

В связи с постановкой такой задачи предполагается, что функции распределения усилий и несущей способности представляются одинаковым законом (например, нормальный). Это предположение основывается на некоторых экспериментальных данных, но не является общим.

В статье предлагается постановка решения таких задач, при которой нет необходимости предполагать одинаковость законов распределения S ext и N ult . В связи с этим используется следующий алгоритм и основные положения.

• 1.    Исходными данными для расчета являются характеристики случайных величин, т.е. параметров, входящих в формулы для S_ext и N_ult :

• —    функции распределения f_s ( x i .) , f_N ( Z j ) , где x i и Z j — случайные величины в количестве i = 1 …k и j = 1 …n ;

• —    математические ожидания соответственно +то

  M s ( x ) = j x i- fs ( x ) dx i , ;

  —то

  +то

  M n ( Z j ) = j j f N ( Z j ) dZ j

  
  

  —то

  дисперсии соответственно

  +то

  
  

  —

  
  

D s ( x i ) = j [ x i ^— M s ( x i ) ] • f s ( x i ) dx i ^,

—то

+то dn (Zj )= j[Zj— MN М'Л (Zj) dZ,;

—то

• -    среднеквадратичные отклонения (стандарты)

• 2.    По выше приведенным формулам вычисляются характеристики S ext и N ult , а именно: M ( S ) и M ( N ) ; D ( S ) и D ( N ) ; a ( S ) и a ( N ) .

• 3.    Используя математические зависимости теории вероятностей для S ext и N ult как для случайных величин можно записать:

^с S ( x i ) = V D S ( x i ) , ^ст N (^Z j ) = ^D N (^Z j ) ;    ⁽³⁾

+x

M (S )= J S ■ f (S) dS;

-X

+x

M (N ) = J N ■ f (N) dN;

-X

+X

D (S )= J[ S - M (S )]■ f (S) dS;

-X

+X

D (N )= |[ N - M (N )]■ f (N) dN.

-X

На основании теоремы о сложении противоположных случайных событий записываются уравнения для любых значений S_ext.i и N_ult.i :

Si

J f ( S ) dS + J f ( S ) dS = 1;

• - X

Nj

J f (N) dN + J f (N) dN = 1.

-X

Nj

Уравнения (4) и (5) являются системой интегральных уравнений. Характеристики M ( S ) , M ( N ) , D ( S ) , D ( N ) равны числам, полученным в п. 2. Решением системы интегральных уравнений определяются неизвестные функции f ( S ) и f ( N ) . Эти функции являются функциями распределения случайных величин S ext и N ult . Они определяются без заранее принятой формы (закона распределения).

Задача определения надежности (определение наступления предельного состояния или его не наступления с заданной заранее вероятностью) решается наложением функций f ( S ) и f ( N ) в координатных осях «частота (вероятность) Р – значения S и N» (см. рисунок) [8, 9]. Заштрихованная область определяет вероятность разрушения, т. е. частоту Р { N <  S } того, что N <  S .

Вопрос о допускаемой вероятности наступления разрушения (предельного состояния) решается на основе экономических соображений и социально-психологических последствий. При установлении допустимой величины вероятности наступления разрушения задача обеспечения ее величины решается по двум направлениям:

• -    смещением f ( S ) вдоль оси S ext и N ult , т.е. изменением величины сил и нагрузок (влево или вправо);

• -    смещением f ( N ) , т. е. изменением вели-

• чины сопротивления, изменяя величины его параметров, их статических характеристик. В анализируемой литературе [13–15] решение данного вопроса не приводится.

Прямое решение данного вопроса состоит в том, чтобы решить следующее уравнение:

cb

J f (N) dN + J f (S) dS = P {N < S},      (6)

ac где правая часть – заданное число, а (a, c, b,) – фиксированные значения на оси S, N (см. рисунок).

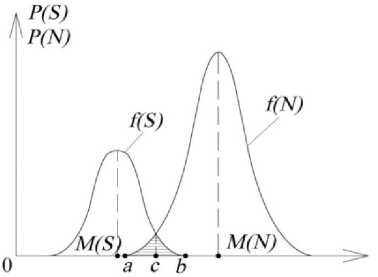
Функции распределения

Для практического применения предлагаемого алгоритма можно использовать упрощение, состоящее в том, что непрерывный интервал интегрирования (- X _+ x ) заменить на фиксированные значения S_i и N_i , используя известные в теории вероятности соотношения, подставляя соответственно при х = S и х = N [7, 11]:

n

M ( x ) = ^ xi' P { x = xi} ;

i = 1

n ²

D ( x ) = ^[ xi- M ( x )] ^ P { x = xi'} .       (7)

i = 1

Ниже приведен пример составления и решения системы уравнений с использованием зависимостей (7).

Пример. Дана функция плотности распределения - f ( % j = 7 ) =0,25; f ( х 2 = 10 ) =0,50; f ( х з = 13 ) =0,25;

Теория расчета строительных конструкций

Средние значения - M ( х 1 ) = ( x 1 + x 2 + х 3 )/ n = 10;

n

M ( х 1 ) = ^ x i P i = 7 ■ 0,25 + ( 10 ■ 0,50 + 13 - 0,25 )/ 3 = 10;

i = 1

Дисперсия - D ( x i ) = ( 7 - 10 ) 2 ■ 0,25 +

+ ( 10 - 10 ) 2 ■ 0,50 + ( 13 - 10 ) 2 ■ 0,25 = 4,50;

Стандарт - ст = J D ( xi ) = 4 4,50 = 2,12.

Решение обратной задачи – определение значений функции плотности распределения, т. е. значений f ( х = 7 ) = Д, f ( Х 2 = 10 ) = Р 2 , f ( х = 13 ) = Р 3 по известным величинам M ( х 1 ) , D ( x i ) , ст ( x i ) .

Для трех неизвестных значений функций плотности распределения необходимо составить не менее трех уравнений:

• 7 Р 1 + 10 Р 2 + 13 Р₃ = 10;

• ■ ( 7 - 10 ) ² Р 1 + ( 10 - 10 ) ² Р ₂ + ( 13 - 10 ) ² Р ₃ = 4,50;

Р 1 + Р ₂ + Р 3 = 1.

Решение этой системы дает следующие величины:

Р 1 = 0,25; Р ₂ = 0,50; Р ₃ = 0,25.

Выводы

• 1.    Вероятностные расчеты позволяют решать задачи обеспечения безопасности и долговечности строительных конструкций и сооружений при накоплении определённой базы статистических данных на момент их создания и в течение эксплуатации.

• 2.    Предлагаемый алгоритм решения задачи о безопасности конструкций и сооружений для сложных конструктивных систем может быть использован при разработки специальных программ для ЭВМ.

При разработке алгоритмов определения безопасности и долговечности необходимо учитывать развитие нелинейных деформаций в материалах конструкций и связанного с этим перераспределения внутренних усилий, рассматривая эти процессы как случайные. В литературе такие разработки отсутствуют.