Система уравнений для расчета формул скорости и методов определения разделительных параметров

• 1.    Аналитические выражения

Дифференциальные уравнения движения частиц по деке аппарата при воздействии гармонических колебаний имеют вид:

X = -gSin α + A ω ²Cos β Sin ω t

Y^.. = -g(Cos α - A ω ²S inβ Sin ω t ) Cos ε ,                                                    (1)

Z = -g(Cos a + Ato2 Sine Sintot) Sin £ где a - угол продольного деки, А - амплитуда колебаний, го - круговая частота колебаний, р - угол колебаний, е - угол поперечного наклона деки. Интегрируя уравнения (1) получим перемещение и

.                                    ..                                                    .

скорости частиц, учитывая по Ньютону, Y out = -RY on ), X out = (1- λ )X on , где λ – коэффициент мгновенного трения, R – коэффициент упругости. Тогда получим:

с I ^{2 п} Р I „

^S X = I          I g

I to j

S_Z = 2 I — Р- I I to J

Cos ( α + β ) 1- λ

-

2Sin α

λ

R Cos α

Sin α -

R+1 t a n β

g Cos α Sin ε

( 2 - X 1 - R —

( X   1 + R

S_Y to n pg I 1 - R                  2 - X I

V _X = —X— =----I---- Cot в Cos a --Sin a I

2 n p to ( 1 + R                   X J

V

S_Z ω

2 π p

n pg I2_- Z - 1- R to ( X 1 + R

Cos α Sin ε

ro₀ 1 + R           A ro ² Sin P

Принимая, что P = — ----, где го0 =--------, получим формулы скорости частиц в направ- п 1- R          gCosa лении оси OX и OZ в виде а I^ О Sin в tan a

V X = A to Cos в---------

I

V_Z = A to Sin в Sin £ — q

I q

,

λ где q = -—-2 - X

1-R

1+R

– параметр сепарации, зависящий от размера, формы и коэффициента трения

частиц. Траектория частиц рассчитывается по формуле dZ V            (1-q)Sin ε

= Z =tanψ = dX   VX        qC otβ -ta nα

Формула расчета разделяющей способности аппарата имеет вид d у d           (1-q)Sin £

D = —— = — arctan ^{v 42}----- ^w dq dq ^ qCot в -tan a

или

D _ψ =Sin ε

Cot в - tana

( q Cot в - tan a ) ² + ( 1 - q ) ² Sin ² £

В.Д. Анахин Система уравнений для расчета формул скорости и методов определения разделительных параметров

Разделительный параметр представлен в виде q=qo

tan α C ot β + Sin ² ε C ot ² β + Sin ² ε

Примем, что поперечный наклон деки равен нулю, тогда (11) примет вид

α o = arc tan ( q o Cot β )                                                                        ( 12)

α o – угол сепарации.

Если угол продольного наклона деки равен углу сепарации α o = α , тогда частицы с q 1 > q o перемещаются вверх, а частицы с q 1 < q o – вниз, где q 1 и q 2 – параметры двух частиц. Уравнение (10) может быть решено для случая максимума разделяющей способности для параметра q o :

D ψ max

Cot2β + Sin2 ε (Cotβ -tanε) Sinε

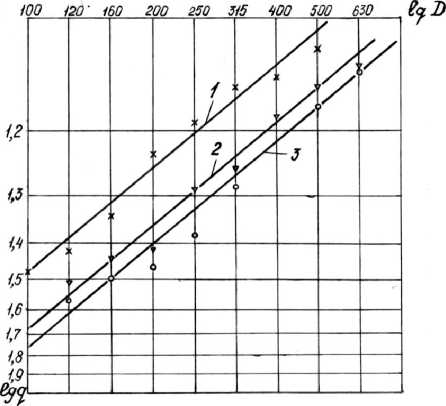
Рис.1. Параметр q = f (D) для покрытий дек: алюминий (1), резина (2,3) для формы частиц: плоские (1,2), изометрические (3)

Заключение

Основными параметрами, определяющими режимы разделения, являются свойства продукта (форма и размеры частиц, коэффициент трения).

• 1.    Параметры, которые могут регулироваться в процессе работы, следующие: угол наклона дек (продольный и поперечный), амплитуда и частота колебаний, производительность.

• 2.    Тип нарифления, материал покрытия, форма деки не относятся к регулируемым, хотя они выбираются в соответствии со свойствами разделяемого продукта, но не могут изменяться оператором по ходу ведения процесса.

• 3.    Диапазон крупности разделяемых частиц составляет 2 – 0, 02 мм Важное значение имеет форма частиц (шарообразная, угловатая, пластинчатая и др.).