Система уравнений электрогидродинамики применительно к электроосмотическим процессам

В работе [1] был проведен анализ стандартной системы уравнений электрогидродинамики (ЭГД) в целях описания физических процессов, протекающих при возбуждении акустической энергии в электроакустическом преобразователе нового типа. Однако (и в [1] это было частично отмечено) стандартная математическая ЭГД-модель нуждается в адаптации к физическим процессам, происходящим в излучателе нового типа. Одной из важнейших физических особенностей изучаемого процесса является наличие двойного электрического слоя (ДЭС) на границах раздела фаз вне зависимости от наличия стороннего электрического поля. Известно, что в ДЭС нарушается условие электронейтральности электрических зарядов в жидкой фазе. В существующих ЭГД-моделях эта особенность не учитывается, в частности при записи уравнения закона сохранения энергии, в котором в выражении для источника джоулева тепла отсутствует учет ДЭС. Кроме того, в системе ЭГД-уравнений для вычисления концентраций электрических зарядов необходимо решать уравнения массопереноса (диффузии), что безусловно усложняет и без того непростую ЭГД-систему уравнений. Вместе с тем в электроосмотических моделях используется аппарат электрохимического потенциала (т.е. химического потенциала электрически заряженных частиц и квазичастиц (ионов, электронов и т.д.) в электрическом поле).

ПОСТАНОВКА ПРОБЛЕМЫ

Работа посвящена учету ряда особенностей электроосмотического процесса в стандартной ЭГД-модели, для чего проводится детализация отдельных уравнений ЭГД-системы, приводятся реальные оценки их параметров, основываясь в частности на материалах работы [2]. Кроме того, необходимо адаптировать ЭГД-систему под решение электроосмотических задач путем привлечения хорошо развитого аппарата электрохимического потенциала заряженных частиц.

РЕШЕНИЕ ПРОБЛЕМЫ

ЭГД-система

Выпишем вначале ЭГД-систему, заимствованную в [3] и представленную в [1] выражениями [1, (15)–(21)]:

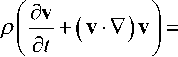
-V p + n A v + P g + f

V- v = 0,

^ + v -V T = _Z A T + — ,         (3)

a t                  pc p

E = ^Ф,                       (4)

d( sE)

j = a E + P e v + s о ^vd t ^+Vx ( P ^x v ) , (5)

V- j = 0,                                   (6)

f = p E - ^ E²Vs + ^ V^f E²p — ) .  (7)

e 2        2 V P J T

Здесь ρ — плотность; v — поле вектора скорости; p — поле давления в жидкости; g — вектор ускорения силы тяжести; f — объемная внешняя сила; η — динамическая вязкость жидкости; T — абсолютная температура в жидкости; χ — коэффициент температуропроводности жидкости; c_p — удельная теплоемкость при постоянном давлении; σ — удельная электропроводность; E — вектор напряженности приложенного электрического поля; ϕ — скалярный потенциал поля E ; P — вектор поляризации; j — плотность тока; ρ_e — плотность электрического заряда в жидкости; ε ₀ и ε — соответственно электрическая постоянная и диэлектрическая проницаемость; E = |E| — модуль вектора E .

В приведенной ЭГД-системе уравнение (1) — это уравнение Навье — Стокса (сохранения импульса) для несжимаемой жидкости; (2) — уравнение непрерывности для несжимаемой жидкости; (3) — уравнение сохранения энергии (теплопроводности); объемная сила f в (1) принимается равной пондеромоторной силе (7), возникающей вследствие приложения к жидкости внешнего поля E .

Представляется целесообразным откорректировать по крайней мере два уравнения из приведенной выше ЭГД-системы (1)–(7): уравнения (3) и (5). В обоих случаях для этого понадобится уточнить формулу (5) плотности тока j . Поэтому первоначально обратимся к вопросу о плотности тока в жидкостях.

Плотность тока в жидкостях

Плотность тока в жидкости неразрывно связана с подвижностью ионов. Подвижность иона u представляет собой его среднюю скорость в жидкости при действии на него силы в 1 Н/м независимо от происхождения этой силы [4, с. 245]. Приведем ход рассуждений при определении ионной подвижности в случае действия поля E (см., например, [5, с. 144]). Подвижность иона определяется из рассмотрения баланса сил трения Стокса Fs и Кулона Fc , действующих на ион с зарядом e . Сила Кулона Fc равна Fc = eE . Сила Стокса Fs равна Fs = -6nnRh ve. Здесь Rh — гидродинамический радиус иона (он обычно превышает реальный радиус иона a вследствие процесса сольватации ионов, заключающегося в том, что вокруг иона концентрируется облако молекул, сцепленных с ним дипольными силами; в [5, с. 145] приводятся порядки этих величин: a ~ 0.05 нм; Rh ~ 0.2 нм). Баланс этих сил при скорости ve дает

F _c + F s = 0 ^ e E = 6nnR h v _e ^

^ v _e = —e — E = u E ^ v _e = —e — E = u E ^ 6 πηR_h              6 πηR_h

e

^ u =-----,

6πηRh где u — подвижность иона. Очевидно, что знак подвижности u совпадает со знаком заряда иона. Как видно из последнего выражения, в случае рассмотрения подвижности ионов u в нарушение приведенного выше определения заряд иона e искусственно внесен в определение подвижности из соображения удобства. В [5, с. 145] приведены величины подвижностей некоторых ионов.1

При определении плотности тока кроме рассмотренных выше сил Стокса и Кулона обычно рассматривают еще одну силу, вызванную давлением на ион со стороны других ионов. Это давление определяется в приближении идеального газа выражением p = ck _B T , а сама сила (обозначим ее

FB) равна FB = -—V(ckBT) [2, с. 22]. Здесь посто-c янная Больцмана kB равна kB = 1.38064852 Дж/К.

Коэффициент диффузии i -го иона D_i связан с его подвижностью соотношением Эйнштейна [4, с. 258]² D i = u i k B T .

Очевидно, что плотность тока jim однотипных ионов с зарядом ei , связанная только со скоростью vei определяется домножением миграционной скорости на плотность заряда этих ионов pei = ciei, Т. е. выражением jim = cieivei = Peivei = PeiuiE (ток jim называется миграционным [4, глава 11], [5, с. 157]). Используя предыдущее соотношение, а также соотношения jim = aiE и vei = uiE, легко получить выражение для удельной ионной проводимости σi для рассматриваемого типа ионов [5, с. 145]: ci = ceu, = PeiUi.

Далее выпишем выражение для вектора суммарной скорости движения этих ионов U _i под воздействием указанных сил, а также с учетом движения самой жидкости [2, с. 24]:

_ V c

^U i = ^V ei - ^Di— + ^V = ^Ui ^E - ^V Di + ^V .         ⁽⁸⁾

ci

Здесь vei = uiE — миграционная скорость рас-Vc сматриваемых ионов; vD = Di —- — их скорость, ci вызванная диффузионными процессами, и v — скорость самой среды.

Совокупная плотность тока рассматриваемого типа ионов получается умножением в (8) совокупной скорости i -го вида ионов U _i на величину плотности заряда этих ионов p_ei = c i e i . Для иона i -го вида получено [2, с. 24], [4, с. 249]³

j i = P e U E - eD V c i + P ei v =

= P ei u i E ^- D i ^V P_a + P ei v = j ⁺ P ei v ,        (9)

j i = P ei U E - D i V p e, = c E - D i V p_ei ,          (9а)

Для совокупной плотности тока с учетом ионов всех типов суммирование последних уравнений дает:

NN j = E ji = E(PeiuiE - DiVPei + Peiv) = j '+ Pev , (10) i=1

NN j' = £(PeiUE-DVPe?) = CE-£DiVPei ,(10а)

i=1

N где pe = E pei — совокупная плотность заряда i =1

N в жидкости; ci = peiUi и с = EpeiUi — парциальная и полная удельная прово=димости соответственно. В (9а), (10а) j'i и j' — соответственно парциальная и совокупная часть плотности тока, равная сумме токов проводимости и токов, вызванных диффузией ионов; ρeiv и ρev — их конвективная часть.

Уравнения типа (9), (10) носят название соотношения Нернста — Планка (см., например, [5, с. 57]).

Далее, допуская наличие в жидкости только па- ры ионов одинаковой валентности, но разного знака, запишем для них выражение (10) для плотности тока, не подразумевая выполнения условия электронейтральности, т.е. pe+ + pe Ф 0 . Имеем Pe 1 = Pe+ , Pe 2 = Pe- , U1 = U + , U 2 = U - , e1 = 9 , e2 = -q . Здесь q заряд иона в единицах заряда протона. Таким образом, p^, = qc1, P- = qc2, где c1 , c2 — концентрации положительного и отрицательного зарядов соответственно. Как отмечено выше, подвижность отрицательного иона является отрицательной величиной. Подставляя приведенные величины в (10), получаем j = E(PeiUiE - Di VPei + Peiv) = i=1

= ( p e u i - p e u 2 1) e - ( D i v p + - d 2 V p e ) +

+ ( P e ⁺+ P - ) V .                            (11)

Как видно, конвективная составляющая плотности тока отлична от нуля.

В случае выполнения условия электронейтральности pe =-p- из (11) следует j = Pt (U1 + U21) E - (D1 VPe+ - D2Vpe) = j'. (12)

В этом случае конвективная составляющая тока пропадает. Если равны и концентрации ионов c 1 = c ₂ = c , и коэффициенты диффузии D 1 = D ₂, то выпадает и диффузионная составляющая плотности тока и остается только ток проводимости j = P e ⁺( U 1 + U 2 1) E = c E .

Однако для равенства коэффициентов диффузии ионов должны быть, как показывает приведенная выше формула Эйнштейна, равны подвижности катиона и аниона, составляющих ионную пару. Поэтому при условии электронейтральности в общем случае для плотности тока наиболее вероятна формула (12).

Как правило, жидкости электронейтральны (см. [4, гл. 11]), однако в случае наличия ДЭС электронейтральность нарушается [4, с. 247], [5, § 8.3], что влечет за собой неравенства концентраций c i ⁺ Ф c i и плотностей зарядов p i ⁺ ^ p i . Тогда для вычисления функции плотности тока j необходимо пользоваться общим выражением (11). Те же рассуждения справедливы при наличии в жидкости произвольного числа пар ионов.

В приложении приведены выражения для плотности зарядов и концентраций в ДЭС.

Коррекция уравнений (3) и (5)

Вначале приведем ЭГД-систему из [2, ч. I, с. 24, 81]:

f d v , ,     1    „     . 1.    p l— + ( v •V ) v I = -V p + n A v + P g + f , 2.    V- v = 0,
3.    | T + v •V T = x A T + Ej , a t                  pc p 4.    Vx E = 0, N 5.    j = j ' + P e v , j ' = ^ E - Z D ^ P e. ,	.    (13)
N 6.    О = Z P e U . , i = 1 7.    f = p E - ^ ° E2Vs + ^ ° Vf E2p ^ ^ | , e     2          2 I     d p J T ’ 8.    V' D = s 00 V-s E = P e , 9.    V" j ' +d pe- = 0. d t

Сравнение этой системы с системой (1)–(7) показывает совпадение уравнений (1) и 1 из (13), (2) и 2 из (13), (4) и 4 из (13), (7) и 7 из (13). Уравнение 3 из (13) отличается от (3) наличием дополнительного источника джоулева тепла в виде плотности тока, вызванной диффузией зарядов

N

- Z D ^ PeA .              (14)

i = 1             J

Отличаются также по форме записи выражения (5) и 5, 6 из (13) для плотности тока⁴. Выражение (6) V • j = 0 представляется неверным в общем случае, т. к. дивергенция от плотности тока V • j (5) при потенциальном поле E (см. 4 из (13)) в общем случае нулю не равна. В [2, ч. I, с. 81] добавлены уравнения Пуассона (8 в (13)) и уравнение непрерывности (9 в (13)). Последнее уравнение представляется избыточным, т.к. применительно к поставленной в работе задаче не используется (например, в рамках одной монографии [2], состоящей из частей написанных разными авторами, в части 1 это уравнение присутствует, а в части 2 отсутствует).

Отметим, что в работе [5, гл. 8] также присут- ствует ЭГД-система, включающая гидродинамические уравнения 1, 2 из (13), а также в той или иной форме электродинамические уравнения 4, 5, 6, 7 и 8 из (13).

На основании изложенного выше может быть записана искомая ЭГД-система, учитывающая электроосмотические эффекты.

ЭГД-система применительно к электроосмотическим явлениям

В искомую систему должны быть включены уравнения 1–8 из (13). Уравнение теплопроводности 3 из (13) должно быть откорректировано с учетом наличия ДЭС и его особенностей, разобранных выше.

Очевидно, что уравнение 3 из (13) при условии наличия ДЭС должно быть записано так cl                E • (j'+ ap v)

— + v •V T = xA T + — --—, dt                      pcp

[ 0 вне ДЭС, а = <

[ 1 внутри ДЭС.

После этого можно записать искомую ЭГД-систему в окончательном виде:

f d v              1

p l — + ( v • V ) v I = -V p + n A v + p g + f ,

V^ v = 0,

— + v •V T = x A T + d t

^E • ( ^j ' ^{+ a} P e v ) ρc_p

0 вне ДЭС,

1 внутри ДЭС,

VxE = 0,(18)

N i=1

^О = Z P e U . , £ = 1

f = p E - E 2Vs + ^° Vf E2 p —1

e 2         2 I    d p J _T

V.D = s„V.sE = Pe.(21)

Кроме того, в условиях переменной концентрации ионов к системе (15)–(21) должно быть добавлено уравнение диффузии (массопереноса) [2, с. 123], однако в рамках решения поставленной задачи в этом нет необходимости, т.к. вне зоны ДЭС концентрация ионов в электроосмотических процессах полагается равновесной, а в зоне ДЭС распределение концентраций ионов может вычисляться без решения уравнения диффузии. Подробности такого подхода приведены в Приложении.

Отметим, что система (15)–(21) не замкнута в том виде, в каком она записана. На этом вопросе остановимся ниже.

Некоторые замечания к ЭГД-системе (15)–(21)

• 1.    Начнем с системы уравнений Навье — Стокса (15), (16). Уравнение (15) — это уравнение сохранения импульса, а уравнение (16) — уравнение непрерывности для несжимаемой жидкости. В случае сжимаемой жидкости вместо (15) и (16) должны фигурировать соответствующие уравнения для сжимаемой жидкости. Например, один из вариантов уравнения Навье — Стокса для сжимаемой жидкости записан в [2, с. 47].

• 2.    Уравнение теплопроводности (17) при наличии конвективного члена v -V T является связанным, т. е. должно решаться в рамках ЭГД-системы совместно с системой уравнений (15), (16) и добавленным к ним уравнением состояния. Если же конвективным членом можно пренебречь, то это уравнение может быть решено самостоятельно после вычисления стоящей справа функции источника джоулева тепла.

• 3.    Уравнения (18) и (21) определяют электростатический характер рассматриваемого ЭГД-процесса. Подробнее об электростатическом приближении можно посмотреть в [2, гл. 1].

• 4.    Уравнение (19) для плотности тока в жидкости выписано в наиболее общем виде. Часто существует возможность пренебрежения тем или иным слагаемым. В случае электронейтральности р_е ^ 0 выпадает конвективная составляющая ρ_e v , а в случае однородной концентрации выпадает диффузионная составляющая.

• 5.    Сила f в (20), называется электрической или пондеромоторной силой. Составляющая этой

Система (15), (16) не является замкнутой, т.к. содержит на четыре уравнения пять неизвестных ( р , p , v = ( v 1 , v 2 , v 3 ) ). Для ее замыкания необходимо добавлять пятое уравнение, например уравнение состояния p = p ( р,s ) , или р = р ( p , T ) , где s — удельная энтропия.

В записи (17) уравнение теплопроводности записано неполно. Например, справа отсутствует член, учитывающий термоэлектрический эффект и член Ф / pc p , где Ф — диссипативная функция. Более полная версия уравнения теплопроводности с учетом стороннего электрического поля представлена в [2, с. 79].

силы — сила Кулона ρ_e E обычно доминирует, особенно при наличии постоянного электрического поля E в проводящих жидких диэлектриках. Второй член — сила, прикладываемая к жидкости при наличии неоднородности электрического поля. Обычно она меньше силы Кулона и может доминировать при приложении переменного электрического поля к изолятору. Третий (потенциальный) член называется стрикционным давлением и может объединяться с гидродинамическим давлением [2, с 124]. Как было показано в [1], при подаче наряду с постоянным электрическим полем и переменного электрического поля при существенной величине второго и третьего членов в (20) могут возникать кратные (паразитные) гармоники колебаний. Это и может являться критерием существенности величины второго и третьего членов в (20), что необходимо в рамках рассматриваемой задачи максимально нивелировать.

Как показано в Приложении, использование стационарности электрохимического потенциала в жидкости и принятие гипотезы об электронейтральности жидкости вне ДЭС позволяет связать с потенциалом электрического поля ϕ в ДЭС (не путать с потенциалом приложенного внешнего электрического поля) концентрацию и распределение плотности заряда внутри ДЭС.

В связи с изложенным выше для замыкания ЭГД-системы (15)–(21) применительно к наличию электроосмотического процесса в жидкости к уже имеющимся уравнениям в качестве недостающих уравнений необходимо добавить уравнение состояния p = p (Р, s) (22)

и уравнение стационарности электрохимического потенциала жидкости ц . ( г ) (см. Приложение, (П1), (П2)):

z х ( С^ ( г ) ^

• V ^ _± ( r ) = 0 ^ к в Т V ln^^ | = ₊ | e |V ф ( r ) . (23) V c о )

Таким образом, ЭГД-система (15)–(23) становится замкнутой и пригодной для решения электроосмотических задач. Введение электрохимического потенциала позволяет при этом избежать решения задачи массопереноса (диффузии). Кроме того, (23) позволяет легко находить в приближении Дебая—Хюккеля такие фигурирующие в ЭГД-системе величины, как c ± , электроосмотический потенциал ϕ и плотность заряда ρ_e .

К системе (15)–(23) для ее однозначного решения необходимо добавить начальные и краевые условия, которые широко представлены в специальной литературе по гидродинамике, электрогид- родинамике и литературе по электроосмотическим процессам.

с ± ( г ) = с о exp

+Ф(г )

k B T

(П3)

ВЫВОДЫ

В работе получена замкнутая система ЭГД-уравнений для такого специфического ее подраздела, как электроосмотические явления. Эта система не содержит уравнения диффузии для поиска поля концентраций ионов, т.к. они могут быть проще рассчитаны в приближении Дебая — Хюккеля. Кроме того, проще рассчитываются электроосмотические потенциалы и плотности зарядов ионов. Наличие в системе уравнения теплопроводности позволяет рассчитывать поле температуры в жидкости, что является крайне необходимым для поддержания необходимого температурного режима при реализации на практике излучателя нового типа (см. [1]).

С учетом (П3) суммарная плотность заряда в ДЭС тогда равна

P e ⁽ r ) = Р ^{+ (} r ) ⁺ Р ^{- (} r ) = | e | ^{[ с} + ⁽ r ) — ^с - ⁽ r ) ] =

= ^{- 2} ec 0 siⁿh J e L ф ( ^г ) .

V ^kB T      )

(П4)

Использование уравнения Пуассона А ф ( г ) =

= - p e ( r ) приводит к уравнению

г

e

А ф ( r ) = 2 ^0 sinh -Ц- ф (г )

⁽ )       ее ₀          ⁷-       ⁽ )

V к в Т

)

(П5)

ПРИЛОЖЕНИЕ

Выражения для распределения концентраций ионов и плотностей их зарядов в ДЭС

Вновь для простоты принимаем наличие пары противоположно заряженных ионов одинаковой валентности. Следуем далее [5, § 8.3]. Все рассуждения основываются на такой величине, как электрохимический потенциал д ± ( r ) , имеющий для ионов вид

Уравнение (П5) является нелинейным и должно решаться численно за исключением ряда частных случаев. Поэтому принято решать уравнение Де-бая—Хюккеля, когда в правой части (П5) учитывается только линейная часть разложения гиперболического синуса в ряд и уравнение (П5) сводится к виду

^А ф ( ^r ) = ТГ ф ( ^г ) .             ^(П6)

λD

(c. ( г ) ^

^ ± ( r ) = ^ 0 + к в Т ln^^ |± | e| ф ( r ) . (П1) V c о )

Здесь | e | = e ₊ ; ц₀ и с 0 химический потенциал и концентрация ионов при отсутствии электрического потенциала ф ( r ) = 0. Термодинамическое равновесие подразумевает постоянство электрохимического потенциала ц ± ( r ) = const, что приводит к соотношению

(с. Гг) ^

к в Т V ln         = + e V ф ( r ) ,        (П2)

V c 0 )

εε k T

Здесь X D = —^{0 в} — длина Дебая. Приближе- ²

e c ₀

ние (П6) справедливо, когда электрическая энергия много меньше тепловой: | e| Z ^ к_вТ .

После решения (П6) и определения потенциала ф ( r ) может быть найдено в приближении Де-бая—Хюккеля распределение плотности заряда

P e ( ^r ) = ^{- ее} 0 ^А ф ( ^г )             ^(П7)

и распределение концентраций из выражения (П3).

Приведем пример таких вычислений для плоской и цилиндрической поверхностей раздела фаз.

где верхний знак в ± и + отвечает положительному иону, а нижний — отрицательному.

В предположении, что при отдалении от границы раздела фаз с ± ( r ) ^ с 0 , ф ( г ) ^ 0, а на поверхности скольжения S_ss (см., например, [7]) потенциал равен дзета-потенциалу ф ( r )| = Z , решение уравнения (П2) сводится к виду

Пример вычислений для плоской поверхности раздела фаз

Плоская поверхность раздела фаз z = 0 [5, с. 148]:

ф ( z ) = ^z exp

P e ( z ) = ^{- ее} 0

d ² ф ( z ) d z z

z >  0;

z λ D

εε ₀ ζ ^λ D ²

z >  0,

(П8)

exp

z λ D

(П9)

c ± ( r ) = c 0 exp

⁺ keT ^{ф( г} )

c ₀

1 + И £ exp ^kB^T

z λ D

(П10)

В (П10) проведен переход от точного равенства (П3) к приближенному с помощью дебаевского приближения потенциала (П8) и линейной аппроксимации экспоненты из (П8). В выражении (П10) отрицательные ионы являются противоионами (поверхность раздела фаз со стороны твердого тела заряжена положительно, см. [5, с. 146, рис. 8.3]).

Пример вычислений для круговой цилиндрической поверхности раздела фаз

Круговая цилиндрическая поверхность (цилиндр радиусом r — a с осью по оси z ) [5, с. 148, 149]:

, .       10 (r / Ad)       , х

ф ^{( r )—z} _т        х ,    ^{( 0} < ^r <  a ) ;

I 0 ⁽ a / ^A d )

(П11)