Системный подход к геодинамическому районированию на основе искусственных нейронных сетей

Объекты ядерного топливного цикла (ЯТЦ) являются источниками радиационной опасности для населения и окружающей среды. Особую экологическую опасность представляют высокоактивные радиоактивные отходы (РАО), содержащие долгоживущие радионуклиды с периодом радиобиологической опасности более 10 лет. При существующем научно-техническом уровне их удаление из среды обитания человека может быть реализовано единственным надежным способом - захоронением в глубокие геологические формации. Выбор площадки для пункта глубинного захоронения РАО (ПГЗРО) основан на поиске структурно-тектонического блока, который обладал бы наименьшей нарушенно-стью при максимальном объеме. Вместе с тем очевидно, что «ненарушенных» участков в земной коре нет, в условиях воздействия нестационарных тектонических полей напряжений структурные блоки разрушаются со временем. В этой связи прогнозирование устойчивости геологической среды, под которым понимается ее способность при всех возможных природных и техногенных воздействиях сохранять или изменять свои свойства в

МИСиС

пределах, не приводящих к опасным смещениям и напряжениям для проектного времени эксплуатации объекта ЯТЦ, является фундаментальным условием обеспечения геоэкологической безопасности.

Информация о геологической среде как системе, находящейся в поле действия природных и техногенных источников, практически всегда недостаточна для принятия обоснованного решения. Прогноз геодинамической устойчивости, прямо связанный с сохранностью изоляционных свойств пород, основан на экстраполяции временных рядов, характеризующих свойства, структуру и процессы в геологической среде. При этом надо ответить на вопрос – насколько далеко можно экстраполировать наши наблюдения (составляющие десятки, сотни, и лишь в отдельных случаях, тысячи лет). Для этого наиболее конструктивным является системный подход, который позволяет в условиях недостатка информации делать долгосрочные прогнозы, используя фундаментальные геологические закономерности, подтвержденные данными инструментальных наблюдений.

Системный подход в приложении к задачам инженерной геодинамики выступает как способ организации исследований, позволяющий выявить общие закономерности. Он основан на изучении геологической среды как системы (рис. 1), которая учитывает такие составляющие любого объекта, как элемент, связь, взаимодействие, а также внешнюю среду [1]. Экзогенные и эндогенные факторы рассматриваются как сложные открытые системы, организованные по принципу иерархической многоуровневой геодинамической системы. Геодина-мическая система – это система с распределенными параметрами, которые зависят от времени t и от координат X(x, y, z) пунктов наблюдений. Поэтому исходные данные рассматриваются как многомерные пространственно-временные ряды, в моделях должны учитываться как детерминированные, так и стохастические возмущающие воздействия [2].

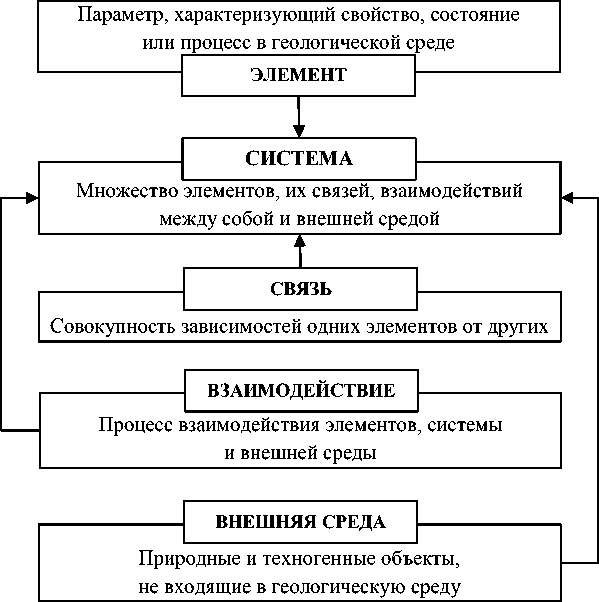
Рис. 1. Схема компонентов системы «Геологическая среда» с учетом [1]

МИСиС

При оценке геодинамической безопасности объектов ЯТЦ необходимо учитывать взаимодействие двух систем – самого объекта и вмещающей среды. Объекты ЯТЦ весьма разнообразны по своему назначению и ранжируются по основным признакам: степени радиационной опасности, геометрическим размерам, времени эксплуатации, глубине относительно земной поверхности и т.д. [3]. В соответствии с главным принципом системного подхода – иерархичностью, т.е. подчинения элементов низшего уровня элементам высшего уровня, тип объекта ЯТЦ, время эксплуатации и размеры определяют пространственно-временной масштаб геодинамических процессов, который мы обязаны изучить при геодина- мическом районировании [4]. Следуя другому известному методологическому принципу – поиску «слабого звена» [1], мы рассматриваем только те параметры, которые оказывают решающее влияние на устойчивость объекта, интегрируя в себе различные виды воздействий (рис. 2). Для приповерхностных объектов ЯТЦ такими параметрами являются смещения и деформации земной поверхности, а для подземных - напряжения в земных недрах. Важную роль при этом играют структурные характеристики среды и упруго-прочностные свойства пород, которые, с одной стороны, служат индикатором состояния среды, а с другой, сами определяют скорость и амплитуды деформаций и напряжений [3].

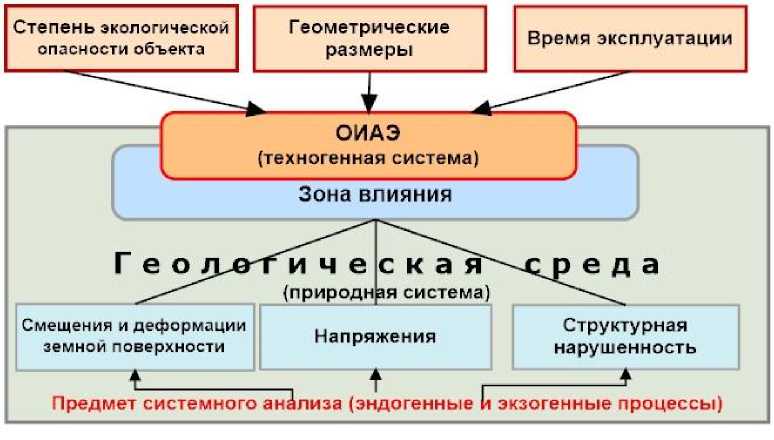
Рис. 2. Схема факторов, влияющих на устойчивость геологической среды при антропогенном воздействии (в виде размещения в ней объекта ЯТЦ)

Требования к геодинамической безопасности объектов ЯТЦ изложены в системе существующих нормативноправовых документов. Определяющими в них являются критерии (предельно допустимые значения), предъявляемые к среде. Например, в СП 11-104-97, СНиП 2.02.01. указаны предельно допустимые значения при проектировании оснований зданий и сооружений: относительное горизонтальное сжатие или рас- тяжение – 10-3, наклон – 3.10-3, относительная неравномерность просадок земной поверхности – 6.10-3, крен основания – 5.10-3.

В этой связи можно предположить, что если среднегодовые скорости деформаций на некоторых территориях достигают величины ε̇ ∼ 3 - 5^.10^-5 год^-1, то они являются зонами повышенной геодина-мической опасности, т.к. за длительный период эксплуатации объектов в таких

МИСиС

зонах могут накопиться деформации, соизмеримые с критическими величинами. В НП-050-03 также указывается, что неблагоприятными для размещения объектов ЯТЦ являются линейные геодинами-ческие зоны, в пределах которых установлены дифференцированные тектонические движения с градиентом скорости четвертичных движений grad V q ~ 10 ⁹ в год и более.

Метод нейросетевого моделирования

Эффективным инструментом выявления закономерностей и связей в экспериментальных данных о состоянии геологической среды являются искусствен- ные нейронные сети (ИНС). ИНС как метод прогнозирования позволяет воспроизводить нелинейные сложные зависимости, которыми и являются геодинамиче-ские процессы в земной коре. С математической точки зрения ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (далее - нейронов). Математический нейрон это искусственный нейрон (персептрон) Маккаллока-Питтса, который преобразует конечные сигналы в выходящую информацию для пользователя (рис. 3).

а

б

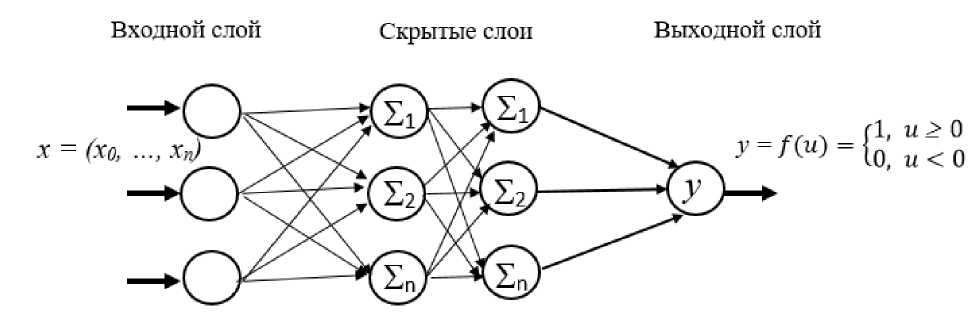
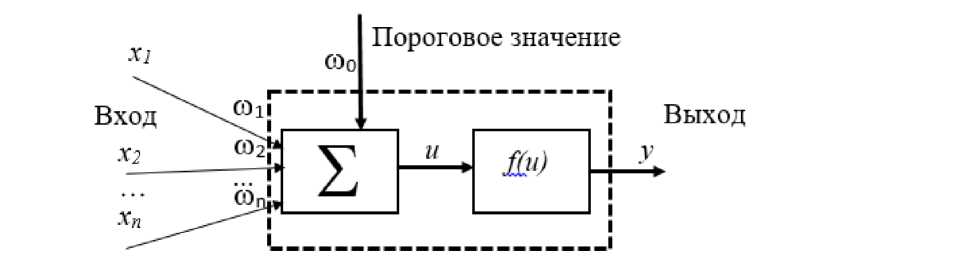
Рис. 3. Персептрон – искусственный нейрон ( а ) и структура многослойной нейронной сети ( б )

Он состоит (рис. 3, а) из вектора входных коэффициентов нейрона x = (x0, …, xn), вектора весовых коэффициентов to = (too, • „, ton) и сумматора нейрона u = ^n_t to, xt . Величину to0 называют пороговым значением нейрона. По существу, в выходном слое получается комбинация всех факторов, опреде- ляющих прогнозируемый геодинамиче-ский параметр, умноженных на соответствующие им весы.

Фактически нейрон вычисляет n -арную булеву функцию вида:

a ( x ) = ф ( Е ” _{= 1} ^to j x ^-to o ) ,       (1)

где ф ( z ) = [ z >  О ] - ступенчатая функция Хевисайда.

МИСиС

Из таких «элементарных» ячеек состоит многослойная нейронная сеть. Взаимодействующие между собой нейроны представляются в виде слоев (выделяют нейроны входящего, скрытого и выходящего слоя) (рис. 3, б ). Задача нейронов входящего слоя - получить, нормализовать и передать информацию на скрытые слои. Далее в скрытых слоях ИНС происходит расчет сигналов, передаваемых на следующие скрытые слои или на выходящий слой.

ИНС имеет ряд преимуществ над статистическими методами [5, 6]:

• -    обучаемость : запроектированная ИНС при поступления новых данных или обновлении старых о состоянии исследуемой природно-технической системы использует их для корректировки своих внутренних параметров и тем самым повышает достоверность своих прогнозов;

• -    многовариантность структуры сети : в отличие от статистических методов ИНС учитывает фундаментальные особенности геологической среды исследуемой природно-технической системы (структурно-тектоническая блочность, влияние разрывов и т.д.), определяющих кинематику современных движений земной коры;

• -    универсальность входящих данных : при обучении ИНС для задач прогноза параметров СДЗК можно использовать геологическую и инженерногеологическую информацию с разными свойствами (статическую и динамическую, качественную и количественную и т.д.).

Для настройки весовых коэффициентов синапсов нейронной сети создаются специальные выборки с измеренными данными. Система сравнивает свое про-

гнозное значение с измеренным до тех пор, пока они не совпадут с заданной погрешностью (рис. 4). Данный процесс -называется обучением. Когда обучение закончено, сеть может использовать свою матрицу весовых коэффициентов для

прогноза.

Рассмотрим схему обучения ИНС более детально. Имеется набор данных,

поступающих на входящий слой сети:

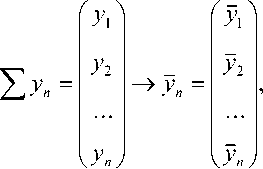
где У;, у 2, .., уп - различные входящие данные; у, у2, .., уи- нормированные

входящие данные (обработанные для использования в скрытых слоях нейронной сети).

Для работы с входящими данными внутри сети необходимо их обработать -

нормировать, т.е. представить числовые параметры не в абсолютных единицах, а в некоторых безразмерных единицах, ха-

рактеризующих относительное значение.

Далее сигналы поступают на скры-

тый слой, умножаясь на соответствую-

щие весовые коэффициенты (изначально

они задаются случайным образом):

s = v xW- = n y n      ij

^у 1

У 2

...

I У п 7

( w

w ^

х

w;

V   ¹ j

, (3)

w

^1j 7

где W j - полная матрица весовых коэф

фициентов синапсов, w ,, w ₁₂, ..., w -весовые коэффициенты синапсов, i - номер скрытого слоя, j - номер синапса в слое.

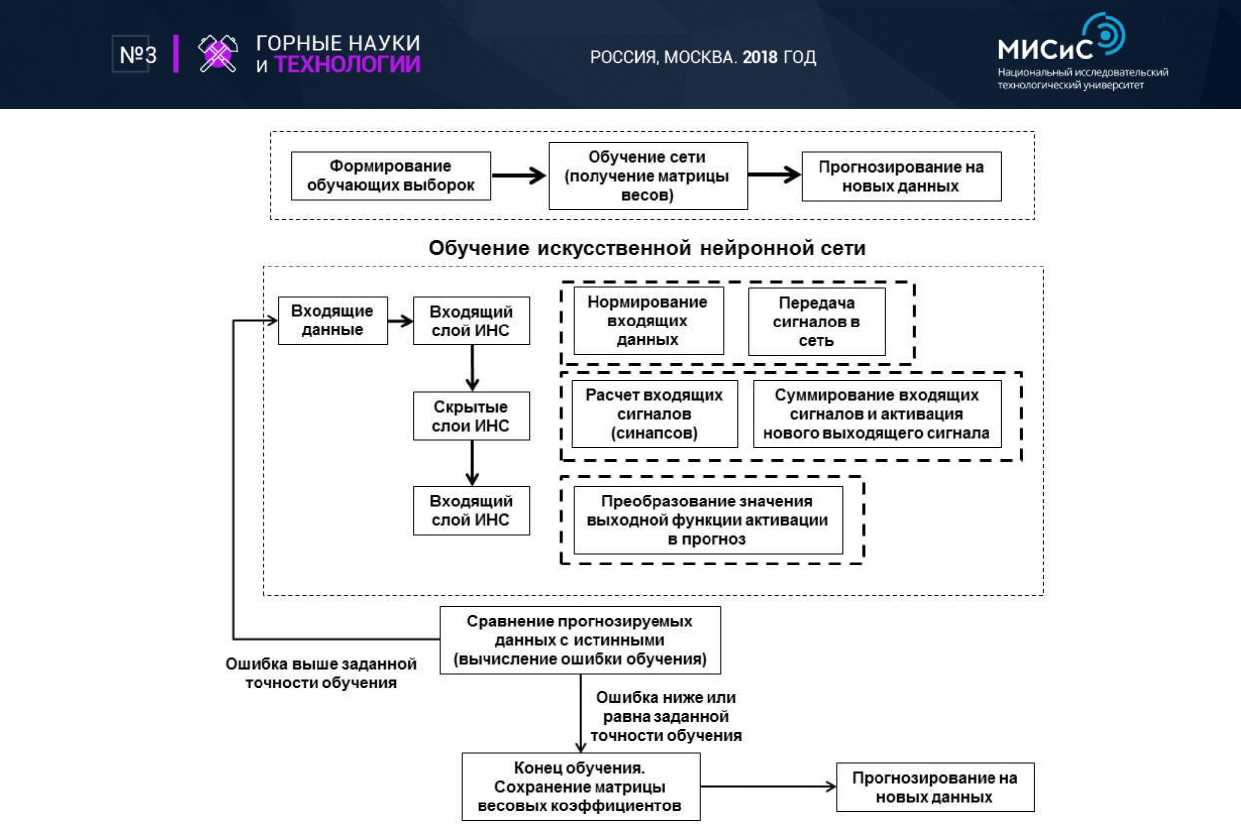
Рис. 4. Схема обучения искусственной нейронной сети

Каждый нейрон скрытого слоя получает сигналы со всех нейронов предыдущего слоя и суммирует их. Далее суммированный сигнал проходит через функцию активации Fact(^Sn), и формируется выходной сигнал. Данная процедура повторяется для всех скрытых слоев.

Сигналы нейронов выходящего слоя – являются прогнозным значением. Прогнозные значения сравниваются с тестовой выборкой, далее вычисляется ошибка прогноза и, если ошибка выше заданной точности обучения, весовые коэффициенты синапсов корректируются и вся процедура повторяется. Иначе обучение считается законченным, матрица весовых коэффициентов сохраняется и может использоваться для прогноза.

Результаты моделирования

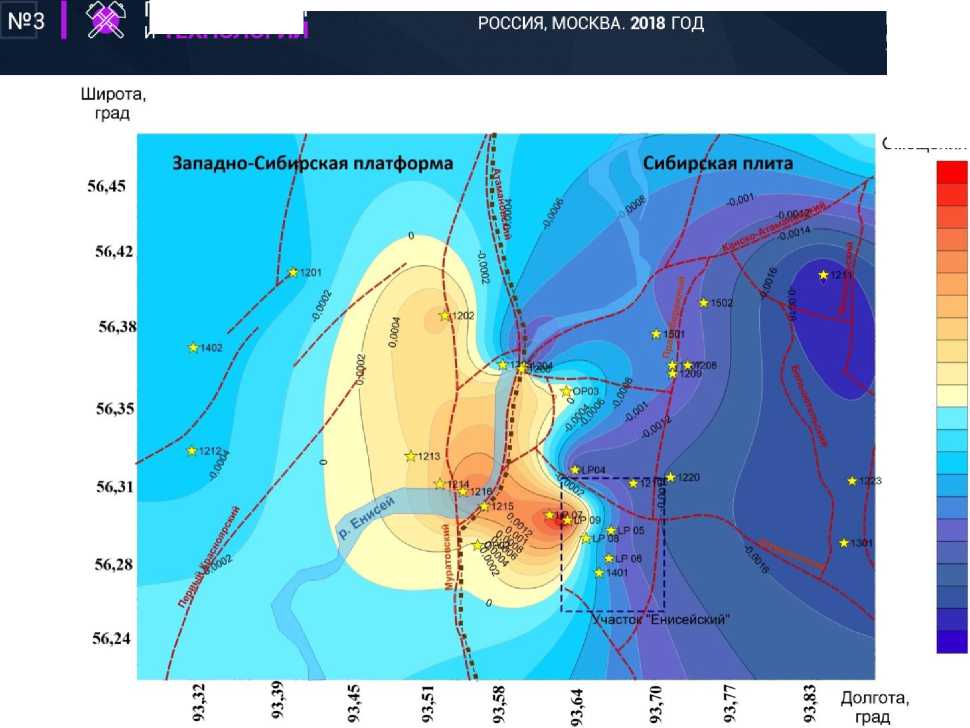
Рассмотрим тестовый пример применения ИНС для прогноза современных движений земной коры (СДЗК) для района Нижне-Канского массива, где, как известно, в настоящее время ведется строительство первого в России ПГЗРО. Из-за физико-географических условий района геодезическая исследовательская сеть построена неоднородно [3]. В южной части (где собственно и планируется размещение ПГЗРО) количество пунктов достаточно мало, поэтому построенные карты СДЗК в точках интерполя-ции/экстраполяции непредставительны. Для оценки качества прогнозов рассмотрим конкретный участок будущего строительства ПГЗРО (на рис. 5 это место выделено пунктиром).

МИСиС^

Смещения XX, м

0,002 0,0018 0,0016 0,0014 0,0012

0,001 0,0008

0,0006 0,0004

0,0002 о

-0,0002 -0,0004

-0,0006 -0,0008

-0,001

-0,0012 -0,0014

-0,0016 -0,0018

-0,002 -0,0022

Рис. 5. Распределение смещений земной поверхности в районе Нижне-Канского массива. Красные пунктирные линии – разломы, желтые звезды – пункты геодинамической сети наблюдений, синяя пунктирная линия – проектный участок для захоронения РАО

Данные инструментальных исследований компонент смещений современных движений земной коры интерполируются вдоль выбранных профильных линий или по необходимой площади. Интерполирование производится на основе известных математических методов - усреднение, полиномиальная регрессия, триангуляция, семейство методов кригинга и методов обратных расстояний и Др. [7]- При интерполяции смещений важно отметить, что расчетное поле смещений содержит в себе неопределённости, обусловленные погрешностями измерений, ошибками аппаратуры, метода и методики проведения наблюдений и обработки данных [8]. Но часто ошибки и неопределенности при площадной интерполяции связаны с тем, что статистические методы интерполяции не учитывают природные особенности (сезонный фактор, цикличность геодинамических дви- жений, зависимость абсолютных величин от масштабного фактора и т.д.) [9].

Прогнозируемые кинематические характеристики СДЗК, получаемые на основе ГНСС-наблюдений, могут быть следующие:

• -    абсолютная величина горизонтальных смещений пункта по оси XX ( W - E ), по оси YY ( N - 5 ) за эпоху [м], U_xx, U yy ^;

• -    суммарная величина горизонтальных смещений пункта по оси XX ( W - E ), по оси YY ( N - 5 ) за весь период наблюдений [м], U *xx , U *yy ;

• -    абсолютная ных смещений за эпоху [м], U zz ;

• -    суммарная

  величина вертикаль-

  пункта по оси ZZ

  
  

  величина вертикаль-

  
  

ных смещений пункта по оси ZZ за весь период наблюдений [м], U *zz ;

• -    скорость горизонтальных смещений пункта по оси XX ( W - E ), по оси YY ( N - 5 ) [м/год], V xx , V yy ;

МИСиС

• -    скорость вертикальных смещений пункта по оси XX ( W - E ), по оси YY ( N - S ) [м/год], V zz ;

• -    дилатация земной поверхности [год^-1], Д;

• -    изменение длины линии между пунктами наблюдений за одну эпоху измерений [+— м], ДL ;

• -    суммарное изменение длины линии между пунктами наблюдений (за несколько эпох) [+ - м], ДL * ;

• -    градиенты вертикальных и горизонтальных движений (изменение амплитуды и скорости движений земной коры на единицу расстояния и в единицу времени), grad U yy , grad U yy , grad U zz , grad V xx , grad V yy , grad V zz .

В тестовом примере мы прогнозировали значение Uхх. Полная выборка (табл. 1) для рассматриваемого участка «Енисейский» состоит из 6 значений параметров для 6 пунктов. В целом же сеть содержит 30 пунктов наблюдений. Для оценки качества прогноза, последова- тельно будем убирать из нее по одному значению, прогнозируя его, используя оставшиеся 5 значений.

Для оценки качества работы ИНС прогнозы деформаций земной коры были рассчитаны и другими (статистическими) методами. Расчеты были произведены на основе двух наиболее распространенных семейств методов интерполяции – кригинга и метода обратных расстояний.

Разберем результаты прогнозов СДЗК различными методами (табл. 3). В столбцах 2, 3, 4, 6 – прогноз сетью очень точный с абсолютной погрешностью до 15 %, в то время как другие методы дают абсолютную погрешность 50– 90 %. В столбцах 1 и 5 – абсолютная ошибка прогноза ИНС высокая 50–100 %, но у других методов она составляет 150– 300 %, также сеть, в отличие от других методов, верно прогнозирует направление (знак) смещения, что очень важно для определения областей сжатия– растяжения участков земной коры.

Таблица 1

Полная выборка движений земной коры для участка «Енисейский»

Пункты GPS	P1	P2	P3	P4	P5	P6
U xx , мм	-15,20	-9,34	-8,99	16,78	-2,33	21,19

Таблица 2 Тестовые выборки
Номер выборки	1	2	3	4	5	6
Пункты GPS	P2	P1	P1	P1	P1	P1
	P3	P3	P2	P2	P2	P2
	P4	P4	P4	P3	P3	P3
	P5	P5	P5	P5	P4	P4
	P6	P6	P6	P6	P6	P5
Прогноз для пункта	P1	P2	P3	P4	P5	P6

Таблица 3

Результаты прогнозов различными методами интерполяции в сравнении с нейронной сетью с использованием данных [10]

Прогноз смещений земной коры Uxx * 10 -4 , м	Прогноз величины Uхх
	1	2	3	4	5	6
Реальные движения	-15,20	-9,34	-8,99	16,8	-2,33	21,19
ИНС	-8,45	-8,78	-7,64	15,79	-4,82	22,39
Метод обратных расстояний	7,62	-0,69	-2,05	11,28	3,19	5,60
Кригинг	12,91	-4,96	-6,69	13,93	4,71	6,28