Системный подход к методической подготовке бакалавров педагогического образования

Как показывает практика, осуществлять методическую подготовку бакалавров педагогического образования в полном объеме только на занятиях по дисциплинам методического цикла затруднительно по следующим причинам:

• •    недостаточное количество часов (например, по сравнению с программами специалитета количество часов, отведенных на изучение теории и методики обучения математике, уменьшилось почти в два раза);

• •    методические дисциплины изучаются достаточно поздно (например, теорию и методику обучения математике бакалавры начинают изучать с четвертого курса);

• •    нет единой системы методической подготовки студентов средствами всех изучаемых ими дисциплин основной образовательной программы;

• •    недостаточно разработана методическая система обучения специальным предметам;

• •    практически отсутствуют курсы повышения квалификации преподавателей специальных дисциплин вузов в сфере реализации возможностей методической подготовки студентов в процессе изучения соответствующей специальной дисциплины.

В связи с вышеизложенным покажем возможность построения элементов системного подхода на примере изучения курса элементарной математики.

Общеизвестно, что обучение студентов педагогических вузов методической деятельности должно осуществляться на протяжении всего времени обучения, в том числе и при изучении специальных дисциплин по следующим основным направлениям:

• •    учет внешней среды (связь содержания обучения в школе и вузе по соответствующей дисциплине, индивидуализация, гуманизация, гуманитаризация, межпредметные связи и т. д.);

• •    реализация на лекциях, практических и лабораторных занятиях оптимально подобранной методической системы обучения соответствующей теме;

• •    подготовка студентов к организации исследовательской деятельности учащихся.

Курс элементарной математики может стать эффективной базой для реализации вышеизложенных идей. Рассмотрим это на конкретном примере реализации заключительного этапа решения математической задачи. По мнению Д. Пойя, Е. С. Канина, Ю. М. Коляги-на, Г. И. Саранцева, Н. А. Зеленина и др., этот этап способствует усовершенствованию решения, более глубокому его осмыслению; позволяет углублять и систематизировать знания; дает возможность приобщения студентов к творческой деятельности; является эффективным средством реализации эстетического потенциала математики, а также мощным средством формирования информационной культуры, что отвечает целям современного математического и методического образования.

Итак, в процессе передачи информации на заключительном этапе решения математической задачи предполагается владение студентов и учащихся следующими блоками действий:

• 1.    Обсуждение задачи и ее решения: осмысление условия задачи; осмысление поиска и хода решения задачи; осмысление результата решения.

• 2.    Поиски и осуществление новых способов решения задачи, их сравнение и выбор лучшего варианта решения.

• 3.    Выдвижение, доказательство или опровержение гипотез.

• 4.    Формулирование и решение новых задач на основе применения методов познания.

Приведем характеристику каждого компонента.

Обсуждение задачи и ее решения

Осмысление условия задачи. Задача сознательно ограничивает требуемую выходную информацию непосредственно узкими учебными целями. Между тем выходная информация очень многих задач позволяет сделать и другие выводы, кроме предусмотренного вопросом задачи. При решении многих задач следует стремиться к достаточно полному исполь-

Поволжский педагогический поиск (научный журнал). № 4(6). 2013

Поволжский педагогический поиск (научный журнал). № 4(6). 2013

зованию содержащейся в них входной информации. Это означает, что многие задачи должны явно содержать несколько вопросов. Если вопрос один, то нередко после ответа на него целесообразно ставить и дополнительный вопрос: что еще можно узнать (найти, вычислить, доказать)? Многовопросность задач приучает студентов к установлению многосторонних связей в рассматриваемых ситуациях. Более полное использование входной информации задачи позволяет экономно распоряжаться временем, выделяемым для решения задач, так как содержащаяся в задаче информация остается, по существу, одной и той же на все время работы с ней.

Осмысление поиска и хода решения задачи. Сам процесс решения задачи и получение выходной информации нередко позволяют делать содержательные выводы. Они могут быть гипотетическими, нуждающимися в обосновании, но они могут быть и окончательными, вполне достоверными. В первом случае возникает новая задача – обосновать или опровергнуть сделанный вывод.

Осмысление результата решения. Сравнивая задачу с решенными ранее сходными задачами, студенты выделяют их общность и различие, лучшие усваивают идею решения данной задачи, глубже познают метод решения класса сходных задач и таким образом готовятся к решению следующих задач.

Поиски и осуществление новых способов решения задачи, их сравнение и выбор лучшего варианта решения.

Данный компонент способствует развитию умения решать задачи различными способами и потребности в этом. Реализация этой цели предполагает формирование умения переосмысливать математические объекты или их элементы в плане новых математических понятий; вычленять, вводить дополнительные элементы или отношения и включать их в новые связи; переводить содержание задачи на язык определенной математической теории.

В методической литературе большое значение придается поискам различных приемов решения задачи. Авторы единодушны в высокой оценке значения таких поисков для развития учащихся. Но не менее важно сопоставление найденных решений, выделение более рациональных и поучительных.

Выдвижение, доказательство или опровержение гипотез, формулирование и решение новых задач на основе применения методов познания.

Назначение данного компонента – научить студентов составлять новые задачи на основе приемов творческой математической деятельности (анализа, синтеза, абстрагирования, аналогии, сравнения, обобщения и т. д.).

Реализация первого действия сконцентрирована на осмыслении условия, поиска хода и результата решения задачи – «взгляд назад» (Д. Пойа) [3]. В результате этого происходят переконструирование, переоценка, систематизация имеющихся у студента знаний и умений. Полученная таким образом информация является не усвоенной извне, а построенной самим студентом.

Реализация второго и третьего действий направлена на развитие задачи «взгляд вперед» (Г. И. Саранцев) [2]. Студент «выходит за рамки задачи», то есть, возвращаясь к отдельным составляющим решения и анализируя их, формулирует на основе решенной новые задачи, объединяет их в блоки, циклы, «цепочки», серии и т. п. взаимосвязанных задач. Таким образом реализуются следующие процессы познания: накопление фактов, выдвижение гипотез, проверка истинности доказательством, построение теории, выход в практику.

Рассмотрим специальные упражнения как средство формирования выделенных действий.

Упражнение 1. Проанализируйте условия следующих задач. Сколько случаев нужно рассмотреть, чтобы решение было полным?

Задача 1. Две окружности имеют единственную общую точку М. Через эту точку проведены две секущие, пересекающие одну окружность в точках А и А1, а другую – в точках В и В1. Докажите, что АА1||ВВ1 (два случая).

Задача 2. Угол АВС равен 60°, причем АВ=ВС=а. Окружность ω1 касается АВ в точке А, а окружность ω2 касается ВС в точке С, кроме того, эти окружности касаются друг друга внешним образом. Найти радиусы окружностей, если известно, что их отношение равно 2 (четыре случая).

Упражнение 2. Решите следующие задачи различными методами. Оцените эффективность каждого их них. Составьте схему решения задачи каждым из предложенных методов.

Задача 3. Внутри прямого угла МРN проведен луч РО. В каждый из образовавшихся острых углов вписана окружность, причем обе они касаются луча РО в точке О. Найдите длину отрезка РО, если радиусы окружностей равны 2 и 3.

• Задача 4. Докажите, что точка пересечения диагоналей трапеции, середины оснований трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Упражнение 3 (на обобщение информации, заложенной в задачной ситуации).

• Задача 5.

• а)    Решите уравнения:

si'n- + cosx = 2 ;

Si?t4x ■ cosx = 1 ;

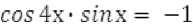
• б)    Каково основное соображение, позволившее вам решить эти задачи?

• в)    Какие другие ограниченные функции известны Вам из школьного курса математики?

Можно предложить студентам задачи-обобщения; часто задачи такого типа выступают как вспомогательные при решении более сложных задач.

• За дача 6. Стороны треугольника равны а, в и с. Вычислите высоту hc (биссектрису lc), проведенную к стороне с.

• За дача 7. Найдите все значения а, при которых расстояние между вершинами парабол у = 2х² + 3ах +1 и у = х² + ах – 3/8 а² меньше √5/2.

Конструирование задач, позволяющих организовывать целенаправленную работу по формированию указанных умений, можно осуществить на материале различных сборников задач, включая в формулировки задач указания выполнить те или иные действия, адекватные процессам получения, переработки, хранения и передачи информации [1]. Для этого необходима лишь небольшая корректировка задач. Приведенные в данной статье упражнения могут служить для преподавателя образцом в осуществлении этой работы.

• 1.    Кузина Н. Г., Сидорова Н. В. Формирование информационной культуры студентов физикоматематических специальностей педагогических вузов при обучении решению задач элементарной математики // Наука и школа 2013. № 4. С. 83–86.

• 2.    Саранцев Г. И. Упражнения в обучении математике. М., 2005.

• 3.    Пойа Д. Как решать задачу. М., 1959.