Системный подход к модели роста деревьев в лесу на основе уравнения Берталанффи

DOI:

Цитирование. Сулейманов Т. И., Асадов Х. Г., Тахмазов Т. М. Системный подход к модели роста деревьев в лесу на основе уравнения Берталанффи // Природные системы и ресурсы. – 2023. – Т. 13, № 3. – С. 21–26. – DOI:

Введение. Понятие системы прочно вошло во все сферы человеческой деятельности, в том числе в науку. На данный момент система не только выступает теоретическим аспектом, но и становится главным элементом в некоторых областях прикладной науки. Системный подход к процессу развития лесов привело к выделению таких показателей развития лесов как скорости процесса гибели и развития (роста) лесов. Указанные показатели леса естественным образом зависят от типа деревьев в лесу, состояния их здоровья и воздействующей окружающей среды [1; 5; 6; 8]. Вместе с тем существует единая обобщенная модель роста и гибели деревьев в виде [2]:

m ( D ) = V ■ g ( D ) - g ' ( D )            ⁽¹⁾

где g'(D) = dg(D); g(D) - функция роста диаметра dD дерева; m(D) – функция гибели диаметра дерева; D – диаметр дерева.

Также существует модель роста, предложенная Фон Берталанффи, применительно к какому-либо показателю развития у [10]. Применительно к диаметру дерева модель Фон Берталанффи имеет вид:

dD m

— = nD - kD, dt

где t – возраст дерева; n , k , m – параметры модели, постоянные величины.

Вместе с тем диаметр деревьев не является единственным главенствующим параметром, показывающим степень развития деревьев. Не менее важным аллометрическим показателем процесса роста деревьев является высота деревьев. При этом между показателями диаметра деревьев и их высотой существует определенная связь.

Как отмечается в [7], традиционно указанная взаимосвязь моделируется линейными уравнениями. В качестве примера на рисунке 1, а , b приведены скаттерограммы, которые могут быть аппроксимированы линейными и нелинейными регрессионными уравнениями.

Отметим во многих работах (см. например [4; 7]) приводятся сложные экспоненциальные регрессионные уравнения зависимости h = f ( D ). Вместе с тем существуют работы, в которых исследована обратная зависимость, то есть регрессионная связь:

D = ϕ ( h ).

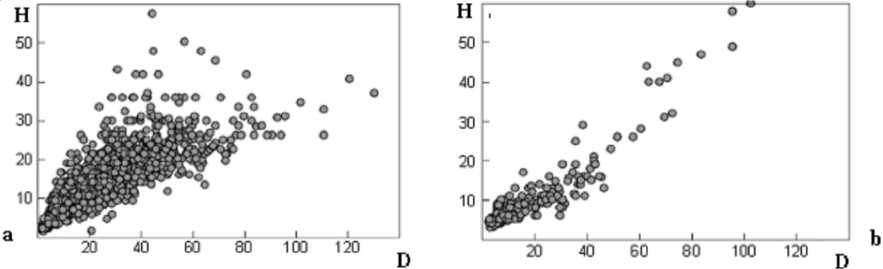
Рис. 1. Скатерограммы статической зависимости h от D :

а – аппроксимированные нелинейными регрессионными уравнениями; b – аппроксимированные нелинейными регрессионными уравнениями

Примечание. Источник: [7].

Например, согласно работе [3], такая статистическая связь может быть охарактеризована квазилинейным регрессионным уравнением (рис. 2).

С учетом вышеизложенного в настоящей статье ставится задача вычисления наилучшей связи между указанными параметрами с привлечением модели роста Л.Ф. Берталанффи.

Материалы и методы

Введем на рассмотрение обобщенный показатель P , определяемый как

P = D ∙ H .                 (4)

В целом показатель (4) определяет продельное сечение деревьев и может оказаться полезным в лесотехническом хозяйстве. С другой стороны, произведение D2 ∙ H ши- роко используется при вычисленьях биомассы в деревьях, что указывает достаточную информативность введенного показателя P. В этом случае для показателя P можно написать модель Берталаффи:

— = nP" - kP . dt

Вместе с тем с учетом (4) имеем:

dP dDdH

=    ■ H + D ■ dt   dtdt

Эквивалентная степень важности показателей P, D, H приводит к мысли о том, что процесс роста может быть исследован с ис-„ _ „ o          л Г dD) „ пользованием составляющих I    I-H или

( dt )

■ D взамен — Далее для определенности dt

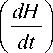
выберем первую составляющую, то есть

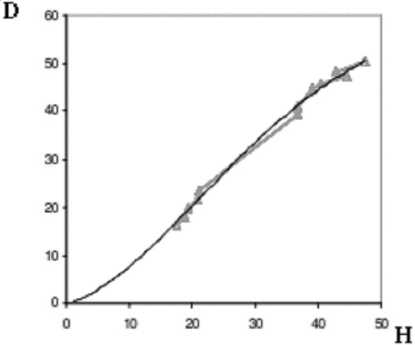
Рис. 2. Квазилинейная регрессионная линия взаимосвязи D = ϕ ( h ) Примечание. Источник: [3].

dD j dt )

к =

• H . В этом случае с учетом (2) и (6)

получим:

H • [ dD |= H • ^ D m - H • kD. I dt )

Очевидно, что (7) повторяет модель Бер-таланффи (2). Далее авторами предлагается следующее усовершенствование этой модели:

• 1.    Учитываем связь между D и H в виде функции:

• 2.    К выбору функции D ( H ) налагается некоторое ограничительное условие, позволяющее несколько сузить пространство непрерывных дважды дифференцируемых функций.

D = D ( H ).

Указанное ограничение имеет вид:

j H max D ( H ) dH = C ; C = const.         (8)

На основе (7) сформируем функционал оптимизации в виде:

j H ^max [ HnD ( H ) ^m - H • kD ( H ) ] dH .       (9)

С учетом (8) и (9) сформируем полный функционал F безусловной вариационной оптимизации:

F = p ” ^HrjD^Hy -H ■ kD(H)^dH +

,              (10)

J о                       J где X - множитель Лагранжа.

Решение задачи (10) в соответствии с методом Эйлера должна удовлетворить следующему условию:

d { HnD ( H ) ^m - H • kD ( H ) + XD ( H ) } ₌ 0 (11) d [ D ( H ) ]                   .

Из условия (11) получим:

mHnD ( H ) ^{m - 1} - Hk + X = 0.        (12)

Из (12) получаем:

D ( H ) = m-j HkH^ (13) mHη

Согласно оценкам, приведенным [9], для многих видов деревьев m << 1. Следовательно, выражение (13) может быть представлено как:

D ( H ) -f - mH! - j m ¹¹¹ (14) I Hk - X J

Как видно из выражения (14) рост H в оптимальном случае должен привести к уменьшению D , что вполне соответствует обычным представлениям о процессе роста деревьев.

Результаты и обсуждение

Что касается самого оцениваемого процесса, то есть в данном случае интегральной величины:

£ - j H max kdH , (15)

то эта величина при решении (14) достигает максимума, так как повторная производная (12) по искомой функции оказывается отрицательной величиной. Для вычисления значения множителя Лагранжа X следует вставить выражение (14) в ограничительное условие (8) и, осуществив интегрирование, вычислить величину X .

Следует отметить, что факт уменьшения функции роста при увеличении диаметра дерева в гомогенных лесах хорошо известно. В качестве примера на рисунке 3 приведены кривые зависимости количества деревьев от диаметра этих деревьев [2].

Проведенное исследование показало, что принятый общий показатель развития при этом оказывается экстремальной величиной, экстремум которой зависит от типа взаимосвязи диаметра деревьев и параметров модели Фон Берталанффи.

Заключение

Целью исследования являлось нахождение такой взаимосвязи между диаметром и высотой деревьев, при которой целевой функционал, составленный на базе модели Берта-ланффи, с некоторым усовершенствованием

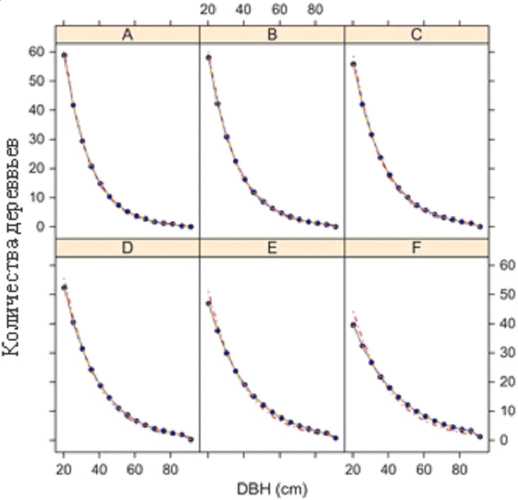
Рис. 3. Кривые зависимости количества деревьев от диаметра этих деревьев Примечание. Кривые составлены для шести разных лесных участков. Источник: [2].

достигает максимума. Усовершенствование модели Берталанффи включает:

• 1.    Наложение интегрального ограничительного условия на искомую функцию зависимости диаметра от высоты дереве.

• 2.    Формирование на базе модели Берта-ланффи целевого функционала, содержащего искомую функцию.

• 3.    Составление и решение задачи безусловной вариационной оптимизации. Нахождение оптимальной искомой функции.