Ситуация blow-up для некоторых нелинейных дифференциальных неравенств

Ситуацией blow-up называют стремление решения дифференциального уравнения или неравенства, к бесконечности в окрестности конечных значений независимых переменных. Теория blow-up решений нелинейных дифференциальных уравнений используется для прогноза. многих катастрофических явлений в физике и технике, в частности обрушения строительных конструкций [1] и фазовых переходов в модели Гинзбурга-Ландау-Аллена-Кана [2].

Большая часть известных результатов в теории blow-up относится к процессам, описываемым дифференциальными уравнениями второго порядка. Метод исследования ситуации blow-up для более широкого класса, задач на. основе использования асимптотических априорных оценок был разработан С.И. Похожаевым и Э. Митидиери [1,3].

В настоящей работе получены достаточные условия возникновения ситуации blow-up для ряда, классов уравнений и неравенств, имеющих сингулярные коэффициенты на. неограниченных множествах, таких как прямые и плоскости, а. также гладкие кривые и поверхности в трехмерном пространстве.

2.    Основные результаты

Пусть S С R” - замкнутое неограниченное множество.

Пусть е > 0, х Е Rn. Обозначим р(х) = dist(х,S) и Se = {х Е Rn : р(х) < е}. Предположим, что существуют положительные константы a, ci,C2,Eo и Ro такие, что для любых е Е (0, Ео) и R > Ro имеют место неравенства ciE“Rn-“ 6 p((S3е \ S2е) П BR(0)) 6 ^((S4e \ Sе) П BR(0)) 6 C2E“Rn-“,        (1)

где Вд(0) = {х Е Rⁿ : |х| 6 R}.

Пример 1. В качестве множества S можно рассматривать гиперплоскость S = Щ = {х = (хі,..., х„) Е R”: х_п = 0}.

Для определенности сформулируем результаты в частных случаях, а. именно для неравенств

(—A)^fc и >  и⁴р - (х) (х Е Rⁿ \ S )                           (2)

с некоторыми к Е N, q, 3 >  0 и

—А_ри(х) >  и⁴ (х)р^-/3(х) (х Е Rⁿ \ S )                          (3)

с некоторыми р >  1, q > р — 1 и 3 >  0. Здесь мы используем обозначение А_ри = div(|Su|^p-2Su).

Неравенства рассматриваются в классе функций п, удовлетворяющих оценке

п(ж) > рж^рДж) ( ж G Rⁿ \ S)                           (4)

с некоторыми константами с >  0, А, ц G R.

Замечание 1. Условие (4) накладывает ограничения на рост решений при | ж | ^ то и р(ж) ^ 0, естественно возникающие в приложениях.

Наши основные результаты о задачах (2), (2’) можно сформулировать следующим образом.

Теорема 1. Предположим, что S удовлетворяет (1). Пустъ q >  1 и

Р > (ц — A)(q — 1) + 2k. Тогда задача (2) не имеет решений и, удовлетворяющих оценке (4).

Теорема 1’. Предположим, что S удовлетворяет (1). Пустъ q > р — 1 и Р > (ц — A)(q — 1) + р. Тогда задача (3) не имеет решений и, удовлетворяющих оценке (4).

Аналогичный результат имеет место для эволюционного неравенства ut — (—A)kп > uqр -1(ж) (ж G Rn \ S; t G R+)(5)

с начальным условием

п(ж, 0) = по(ж) (ж G Rn \S).(6)

Предполагается, что начальная функция по(ж) удовлетворяет оценке п0(ж) > рж^рДж) (ж G Rn \S)(7)

с некоторыми константами с >  0, А, ц G R.

Типичный результат о задаче (5), (6) можно сформулировать следующим образом.

Теорема 2. Предположим, что S удовлетворяет (2). Пустъ q >  1 и по удовлетворяет

• (7)    с• q > max{P > (ц — A)(q — 1) + 2k, 0}.

3.    Доказательство теоремы 1

Тогда задач,a (5), (6) нс имеет решений.

Замечание 2. Отсутствие решений задачи (5), (6) называют ситуацией мгновенного разрушения решений (instantaneous blow-up).

Введем семейство пробных функций р = фр G C0^k (Rⁿ \ S; [0,1]) вида

Рд(ж) = £1 (ж)рр (ж), д е к > 2kq‘. ^i G C2k(Rn \ S; [0,1]) такими, что д

< д ( ^{ж )} = {

0 (ж GS1/д U (Rn \S4/д)), 1 (ж GS3/д \S2/д), и рд G C0k(Rn; [0,1]) такими, что

(тЛ = / 1 (| ж | 6 ^Д), ^рд( )    ( 0 (| ж | >  2R).

Структура этих пробных функций позволяет избавиться от особенностей на S и на бесконечности. Будем считать, что существует константа c >  0 такая, что

ID“^ 1 ( ж )| 6 cR^w д

( ж G Rⁿ),

и

|^“Рд(ж)| 6 cR~^W     ( ж G Rⁿ)

для всех мультииндексов ас 0 6 |а| 6 2к.

В примере 1 можно выбрать £ i (x) = £д (x _n ) и ^д(т) = Дд(|x‘|), где д       д

/п - 1

^|x ‘| = J Е ^x 2 it

у р^у

(|жп| 6 1/R ИЛII |ж„| >  4/R), (2/R 6 |ж п | 6 3/R),

7 / а ^д(x) =

( 1 (x‘ 6 R), [ 0 (x‘ > 2R).

Теперь предположим, что решение и задачи (3), удовлетворяющее (4), существует.

Умножая обе части (3) на рд и интегрируя по частям, получаем

/

u^qр ^Др д dx 6

j и( — А)^кр д dx 6

/

и| A^kр д | dx 6

откуда

supp ^ д

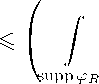
uq р

supp ^ д

1 q

^Др д dx

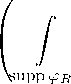
Bq'                 ‘         ‘ рT |Afcрд|q рДq dx

supp ^ д

/

u^q р ^Д р д dx 6

/

Bq '                 ‘         ‘

P ^|Ард^ р^г_д^{Ч dx}.

supp ^ д

supp ^ д

В силу выбора рд мы можем уменьшить области интегрирования в обеих частях неравенства:

u^qр d p K dx 6

Bq' ,           ‘          ‘ р~ |Akрд|q ргдч dx.

(5 3/ ^д\ 5 2/ ^д ) П В д (0)

(5 4/ ^д\ 5 і/ ^д ) П В 2д (0)

Заметим, что рд = 1 во всей области интегрирования в левой части неравенства.

Используя условия (2), (8) и (9), получим

Rq(A—д)—Д+п—2а 6 ^R— ^q"" +2^q'+п—2а что приводит к противоречию при 3 > (А — p^(q — 1) + 2к и R ^ то.

Замечание 3. Можно обобщить этот результат на более широкий класс стационарных дифференциальных операторов высокого порядка с постоянными или переменными коэффициентами, в том числе на системы вида

Г (— А)^к и > r^qр^-а(x) (x £ Rⁿ \S ), ( (—А)г >  у Р р ^{- Д}(x) (x £ Rⁿ \ S )

с соответствующими параметрами к, I £ N, p,q >  1, a,3 £ R-

4.    Доказательство теоремы 1’

Здесь мы умножаем обе части неравенства (3) на н ^ р д с 1 — p < у < 0. Интегрируя по частям, получаем

J u^{q +} ^ р ^Др д dx 6

R ⁿ

= у

р."

I u^7-1|Du|^pр д dx +

J (|Su|^{p 2} Du, В(и^ур д )) dx =

R "

/

6 у

I и^{7 1}|Dи|^pр д dx +

R "

R "

/

R "

| Du | ^{p 2} ( Du, Dр д ) dx 6

|Dи|^p-1|Dр д | dx,

и в силу неравенства Юнга

j H^q+pp ³pRdx + Д| j u⁷ 1 |Du|^pp R dx 6 ^\$^^ + сЩ Г^. DpTp^,

R "

R "

т. е.

j u^g+7 p ³ p r dx 6 c(y) I u^ 1 |Dp|^p р^{1 p} dx.

R "                        R "

Повторно применяя неравенство Юнга, приходим к

2 / »g+v

R "

Р^+Т)   «'Д ■ p I )    1

^pP R dx 6 c(y)    l Dp l s ^{- p+1} p q ^{- p+1} р

R "

Сужая область интегрирования, получим

n^{q +} p

³ P R dx

Р ⁽ 9 ⁺ Т) ч - р+1 dx.

в левой части этого неравенства

(В ³ / ^д\ В ² / ^д ) П В д (0)

u^g ' ' p-d dx,

(5 ³ / ^д\ 5 ² / ^д ) П В д (0)

а в правой части - р^+т) Рт+Р-1)  1

pCs+t) ч - р+1 dx.

І Вф І ч - Р⁺¹ p Ч - Р+¹ р

(5 ⁴ / ^д\ 5 ¹ / ^д ) П В _2Д (0)

Используя условия (2), (8) и (9), аналогично предыдущему пункту, получим

_R .....    2 . 6 _cR +    2

что при предположениях теоремы приводит к противоречию при R ^ то.

Замечание 4. Этот результат можно обобщить на более широкий класс существенно нелинейных стационарных операторов, в частности, на системы вида

J —A_pu >  v^sp ^- “ (x) (x E Rⁿ \ S ),

I — A g v > H p ^{- 3} (x) (x E R ” \ S )

с соответствующими параметрами p,q > 1, s, z,a,P E R.

5.    Доказательство теоремы 2

Для задачи Коши (5), (6) введем два семейства пробных функций, а именно p r ( x ) по пространственным переменным и Д (t) по времени. Здесь p r ( x ) определяется аналогично предыдущему пункту, а Т_т E С 1 ([0,т]; [0,1]) с т > 0 таковы, что

^Т т ^(t) = { 0

(0 6 t 6 т/2), (3т/4 6 t 6 т )

и, кроме того,

3т/4

f IT T |^g

J |Т т |^g’^-1 т/2

dt 6 ст ^{1- д} ‘

(Ю)

• с некоторой константой с > 0.

Умножая обе части (5) на p r (х)Т_т (t) и интегрируя по частям, получим

J Т_тdt J u^qр ³P R dx + J u o P R dx 6

R+     R”

• 6    j Т_тdt J u( — A)^k p r dx — У Т Т dt У up R dx 6

R+

R +      R ”

• 6    J Ттdt J u lAkpRldx + J Т\dt J upRdx. R+     R”              R+

Применяя к обоим слагаемым в правой части неравенства параметрическое неравенство Юнга, получим

2 У Т_тdt J u^qр ³P R dx + У u o P R dx 6

R ₊      R ”               R ”

6 d У Т т dt У |A^k pr^ р ^-^ p R-^ ’ dx + C 2 У |Т т |^q' Т^'dt У р^-4 pV dx

R +

R ”

R +

R ”

с некоторыми константами c i ,C 2 >  0.

В силу выбора p r (x) и Т_т (t) мы частях неравенства:

2т

. / Т т dt     /

⁰         ( S 3/^R \ S 2/^R )n B _R (0)

можем уменьшить области интегрирования в обеих

2т

6 C i У Т_т dt

2 т

/

u^qр ³P R dx + У       u o P R dx 6

( s ^3/R \ s 2/^R )n B _R (o)

‘ Рч'          '

A prV р^pR^q dx+

(5 4/ ^л\ 5 1/ ^л ) П В 2д (0)

+C 2 У |Т т |^q'Т_т^1-q'dt        У р⁴pR^_q' dx.

^т                  (s 4/ ^R\ s 1/ ^R ) n B 2R (o)

Заметим, что первое слагаемое в левой части неравенства неотрицательно и p r ( x ) = 1 во всей области интегрирования. Используя условия (2) и (7)—(10), получим

_Rn-2 _{a +} X ^- _R 6 сД^и-2 “ ^- 4 — 1 т ( т ^- 5- г + R 42 - 1 ) .                    (11)

Легко видеть, что правая часть (11) достигает минимума при т = cR-2k.                                       (12)

Подставляя (12) в (11) и устремляя R ^ то, приходим к противоречию.

6.    Вывод

Мы доказали основные результаты, сформулированные в разделе 2, об условиях возникновения ситуации blow-up для стационарных и эволюционных полулинейных дифференциальных неравенств высоких порядков по пространственным переменным, а также для квазилинейных эллиптических дифференциальных неравенств второго порядка.

Аналогично можно получить условия разрушения решений для других классов дифференциальных неравенств, таких как:

• •    полулинейные и квазилинейные эллиптические системы,

• •    эллиптические неравенства с градиентными слагаемыми,

• •    более общие эволюционные дифференциальные неравенства и т.д.