Ситуационная надежность конструкций сооружений при периодическом контроле их состояния

Ситуационная надежность как комплексное свойство строительной конструкции заключается в ее способности выполнять заданные функции, сохраняя свои основные характеристики в установленных пределах, в условиях сложившихся на данный момент нагрузок и воздействий, в сопоставлении с измеренным потенциалом сопротивляемости конструкции сооружения, т.е. при оценке в режиме реального времени.

Для не резервированной конструкции сооружения обозначим параметр потока отказов о , интенсивность восстановления:

ц

ТBn T Kn где (T Bn -T Kn ) – среднее время восстановления.

При долговременном периодическом контроле конструкция сооружения в момент освидетельствования может быть в одном из трех состояний:

• –    работоспособном, т.е. с потенциалом внутреннего сопротивления, достаточным для полной компенсации внешних воздействий – Д 1 ;

• –    неработоспособном, с необходимостью временной разгрузки на период восстановления – Д ¹ ;

• –    неработоспособном, с восстановлением до нормативного уровня, без снятия нагрузок и воздействий – Д 2 ;

В общем случае вероятность состояний конструкций в момент времени T (t), отсчитываемый от предшествующей (n - 1) проверки, не зависит от частоты контроля при п^да. Для контроля с по- стоянным периодом

Х^ Kn + 1

—

T ) = a t = const соответствующие вероятности состояний p ( t ) , p ( t )

и p ( t ) можно определить из принятых зависимостей:

P 1 ( t ^{) =}-

—

—цА t| — o t L      — о A t| —,

e )e — (1 — e )e

ц

.

L     — ц А t\   о /-      — о A t\

(1 — e )— — e ) ц

P 2 (t )=-

—

— - t

e

— - A t —        — - A t

^{( 1 —} e ^)— 7^{(1 —} e ) ^—

P 3 ( t ) = 1 — P 1 ( t ) — P 2 ( t ) •

При усреднении этих вероятностей по времени

P = ( 1

(1 — e

- “>

——A t\- — — e )--------•

-— A t ;

——A t    —        ——A t e   )—;;(1 — e )

—

P, _ ¹ — (1 — - ) P , •

-

При случайном периоде контроля с промежутком времени T , не зависящим друг от друга и

имеющим некоторое распределение со средним значением ^A t и коэффициентом вариации _ < 7 ( t ) , v

решение может быть следующим.

Обозначим стационарные значения соответствующих вероятностей через Р 1 , Р 2 и Р 3 . В этом случае при условии —<<- состояния конструкции сооружения могут быть приближенно описаны маркое-

ским процессом с графом переходов (рис.1), где q _

A t (1—v2)

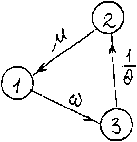
Рис. 1. Граф переходов марковского процесса, отражающего состояния конструкций в процессе эксплуатации

Значения вероятностей состояний здесь определятся из системы линейных алгебраических уравнений:

——P1 + -P 2 _ 0;

^— - ^P 2 + Qq P 3 = ⁰;

— P r P 3 _ 0 . q

с условием нормирования ^ p _ 1 .

i = 1

Решение уравнений (5) дает следующий результат:

P 2 =

P 3 =

При экспоненциальном законе распределения периода контроля q _ a t задача имеет точное решение.

Наиболее распространенными среди строительных конструкций сооружений являются железобетонные. Внутренний потенциал сопротивления каждой из них определяется условиями конструктивной прочности:

– надежная совместная работа арматуры с бетоном:

;

сц .

• -    бетон конструкции должен воспринимать сжимающие усилия от действующих моментов и продольных сил:

R' ^Rx = f MN)];(8)

• -    восприятие бетоном конструкции сжимающих или перерезывающих усилий от поперечных сил:

R'' ^Rx = f (Q))];(9)

• -    арматура должна воспринимать действующие усилия от момента, нормальных и поперечных сил:

R'I ^Rx = f M N Q ) )1;(10)

Здесь r' - R' - внутренний потенциал сопротивления (измеренные прочностные характеристики) элемента, узла конструкции в расчетном сечении; r - контрольные значения, полученные по рас- чету в сечении с координатой ; M N Q - соответственно расчетные значения момента, продольной и поперечной сип в сечении с координатой , ; т - сопротивление сцепления арматуры с бетоном.

Диагностируемыми параметрами являются действительные геометрические размеры и соотношения, а также прочностные характеристики элементов:

R ' ^ A s R b ^; R I' ^ A b R b ^; R ' ^ AR ^; R IV ^ A s R s •

Здесь A и A - площадь сечения соответственно арматуры и бетона, R и R - прочность арматуры и бетона.

Интегральная оценка несущей способности опасного сечения (система его параметров r ' - R ' характеризуется одномерностью пространства признаков и при возможной взаимокомпенсации имеет два состояния: D - исправное и D - требующее ремонта.

Правило решения состоит в следующем:

^при x >  , 0 x ^ D 1 ^{; при} x <  X o x ^G D 2

В зависимости от факторов, входящих в систему (R - R') распределение x для исправного и требующего ремонта, состояния могут пересекаться (рис. 2).

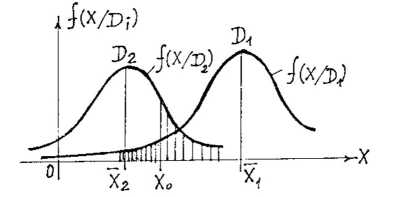
Рис.2. Статистические распределения плотности

X вероятности диагностического параметра

~ -Л, л, для состояний и

Согласно техническим нормативам такая конструкция бракуется, поскольку невозможно выбрать значение x0 , при котором правило (10) не давало бы ошибочных решений.

На наш взгляд, решение данной диагностической задачи может быть осуществлено по одному из следующих вариантов:

• -    выбор оптимальной величины , ₀, исходя из уровня экономически целесообразного риска (методы минимального риска, минимакса, Неймана - Пирсона и т.д.);

• -    переход к оценке конструкции сооружения по измеренным на натуре параметрам, с уменьшением на этой основе величины дисперсии;

• -    дифференциальная оценка элементов и сечений конструкции по условиям r ' - r '^v как много-

• мерной случайной величины.

Если известна цена возможного ремонта (усиления) конструкции С 21 , цена контроля С 12 и цена правильного решения Си <0, то величина риска (см. рис.2) запишется:

” ( )                 x ⁰ ( )

z = C 11 P 1 J f l x I dx + C 12 P 1 J f l x I dx +

^-» V D 1 )             -^ V D 1 )

^ 11         ^{x 0} 11

C 2. P 2 J f l x I dx ⁺ ( C 11 - C 2. ) J f I x l dx "

-* V D 2 )                 -* v D 2 )

Учитывая очевидные равенства

X ( 1 X ( 1

получаем

I f n l dx ^-1   I f X I dx =^r

-” l D i )           -„ l D 2 )

z

x 0

= C 11 P i + C 21 P 2 + I

-X

1                                                                                                      1

C12 P1 f X|-( C 21 - C11) P2 f X| l D1)                lD 2).

dx .

Поскольку два первых слагаемых постоянные, то зависимость z от x определяется величиной интеграла. При малых подынтегральное выражение отрицательно [распределение x лежит пра-x                                                                   f ( D1)

вее

f ( x

больших x оно положительно.

Для выбора x , соответствующего zmin , следует начать интегрирование с сечения x = x0 , в ко тором подынтегральное значение положительно при   > x0. Изменение знака подынтегрального выра- жения произойдет в сечении x0 , причем

Г* Р f I ^x 0/    I             \Р fl ^x 0/    I = 0 или

C 12 P 1 f / D C 21 C 11/ P 2 f / ТЛ ⁴ l / D 1 )               l / D 2 )

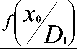
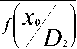
⁽ C 21 - C 11 ) P 2

C 12 P 1

с прежним правилом решения (10).

Например, параметр x имеет нормальное распределение при D1 и D состояниях с одинако- вой дисперсией. В этом случае

—

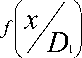
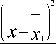
2 ct ²

_— | ²

^X — X 2 ) 2 c 2

C

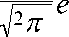
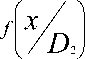
C

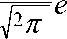
Внося эти соотношения в (14) и логарифмируя, получаем

Из этого уравнения

ln

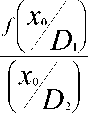
T¹^² X о I X 1 ² C    ^l

x о ^- 2 1 x 1 ⁺ x 2

—

C

L 2    2 -

^- X 2 l ⁺ X 2 ^- X 1 - In

X 1 ⁺ X 2

/

l

P 2

In 25" + ln

P 1

⁽ C 21 - C 11 ) P 2 .

C 12 P 1

⁽ C 2. ^- C .. ) 1

C 12    )

при правиле решения (10), т.е.

X > X0 X G D1; при D 2 X G D2.

Дискретная оценка несущей способности сечений железобетонной конструкции по каждому из условий конструктивной прочности R - R I предполагает статистическое решение многомерного распределения. Состояние системы ( R - R I ) характеризуется вектором

X -{X1,X2X3,X4}.

Статистическое распределение диагностических параметров (R - RI) для состояния D f 3 V

D 1 7

x 1^, x 2 x 3^, x 4

= f V /D

.

При статистической независимости этих параметров

^f X f

V

л

D 1 7

= fI X1/_  I fl X2/  I fl Xз/_  I fl X4/ ffff

V / D 1 7 V / D 1 7 V 7 D 1 7 V 7 D 1,

.

Аналогично плотность распределения диагностических параметров для состояния D

f ( х V

D 2

= f I ^XV I f\ ^X 2/ I f\ ^X3/ I f ^X 4/ ^{f f f f}

V D 2 7 V D 2 7 V D 2 7 V D 2

.

Правило решения принимается следующим:

^

^

^

^

XG W.,то XG D1; XG W2,то XG D2.

^

То есть если точка, соответствующая вектору x находится в области W

, то конструкция нахо-

дится в состоянии D , и аналогично для области W . В ставить как

соответствии с (14) правило (19) можно пред-

при f I X

f I ^х/

D11 _>  ⁽С 21 - C 11 ) P 2 >

^

X G D1

C 12 P 1

D 1

f ^ /I

при f x

Vz

[X/ f 7

V

D 1

____7

/7

D 1

7 c 21 — c J p 2

^

XG D2

C 12 P 1

Поскольку принято, что параметры х ( R I _— R I ) статистически независимы и имеют нормальное распределение, то в соответствии с равенством (17)

f [ ^х

V

\

D .

n = 4

n— ■^—1 СТ , (1)

f — I²

, i х г х „1) J .

e ^ст , (1)

4 2П

где X _{1 (1}) , X , (2)

f ^

f X

л

V

D 2

n =4                             ! ^X ‘ ^X ‘ ^|2 > 7

= n--- TT- e"СТТ •

- ^—1 ст „)7² п           .

– средние значения -го диагностического параметра для состояний D и

D 2 ; СТ , (1) ,

СТ ² - соответственно их дисперсия.

Логарифмируя условие (20), получим

При ln ffX/)                  xg Dr

D 1

4—4>in P ¹+in ^ n n

J X/ I ^{P 1}

^f I / D 11

⁽ С 21 - C ,, )

C 12

Используя соотношение (22), имеем

При , n = 4

1У )

2 -7

x i

—

—     Л ²     f

X , (1) )       I X ,

—

— л ² 1

X , (2) I

ст - (1)

—

СТ , (2)

C „ — C l, >  ln P ² + ^ln “ C 1T P 1

—

n=4ln ^(7) X G D1 (24)

^{= 1}         СТ (1)

Если дисперсия для состояний D 1 и D 2 одинакова, то правило решения упрощается, т.е.

при ^

i = 1

x i (1)    x i (2)

Q .

1 Г -        -

2 1 x i (1) + x i (2) - x i

, P ^, Gr G , >^ln P +'V

при £ i=1

Q .

x i (1)    x i (2)

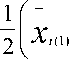
⁺ X . (2)

<

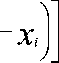
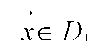
<1 nP2 +1 nC2^1 lnP1 ln C12

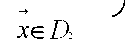
Исходя из (25) следует, что в данном случае наиболее важна разность между отдельным значением параметра и средним значением. Это положение необходимо учитывать при разработке инженернотехнического и методического обеспечения системы контроля и принимать во внимание, прежде всего, изменение параметра, а не его абсолютную величину. Из (25) также ясно, что если средние значения параметров для двух состояний ( D и D ) совпадают, то соответствующая координата не влияет на классификацию.

Q i (i) = Q i (2) = Q i = const ,

поэтому правило решения (25) может быть эф-

Все это при условии, что фективно реализовано только в системе долговременного регулярного контроля в процессе эксплуатации со скважностью, формируемой на основе (1) - (6).