Сканирующие свойства дифракционного элемента, формирующего аксиально-симметричный дифракционно-ограниченный волновой пучок

На примере рассмотрения дифракции скалярных волн на амплитудном бинарном дифракционном «линзаконе» показана возможность сканирования в пространстве дифракционноограниченным волновым пучком при смещении точечного источника излучения и изменении длины волны излучения от расчетной в террагерцовом диапазоне длин волн.

В последнее время значительный интерес проявляется к свойствам дифракционно-ограниченных волновых пучков (ДОВП), являющихся следствием решения волнового уравнения. Для получения ДОВП [1] при плоском падающем волновом фронте обычно используются стеклянный конус в оптике [2], диэлектрические конусы в СВЧ [3] и миллиметровом [4] диапазонах длин волн. Другой метод формирования ДОВП в оптическом диапазоне состоит в использовании дифракционной оптики [5].

В настоящей работе на примере дифракционного элемента, предназначенного для работы в субмиллиметровом диапазоне, показана принципиальная возможность сканирования дифракционноограниченным волновым пучком при смещении точечного источника излучения от оптической оси. При этом фокусирующие свойства дифракционного элемента сохраняются в широком спектральном диапазоне как для осевого, так и внеосевого положения точечного источника излучения.

Формирование ДОВП проводилось с помощью амплитудного бинарного дифракционного элемента (ДЭ). Схема формирования дифракционноограниченного пучка показана на рисунке 1.

Отсюда

sin Y , 1 П

Гк = -c---2— +---2— cc - F cos Y, cos y cos Y

c = F 2 ² + a ² + a sin y + к X .

Полученное выражение для границ зон показывает, что период зон в таком дифракционном элементе не остается постоянным, а изменяется вдоль радиуса. Выбором величины опорного радиуса возможно в определенных пределах регулировать положение начала линии фокусировки на оптической оси.

Из приведенного построения дифракционного элемента для формирования ДОВП легко видеть, что длина отрезка фокусировки и ряд фокусирующих свойств рассматриваемого дифракционного элемента определяются углом у падения излучения на оптическую ось. Оценим, как влияет изменение длины волны излучения от расчетной на параметры области фокусировки. Из выражения для радиусов зон на поверхности плоского элемента легко получить, что

Y = arcsin

F ²

+ r k

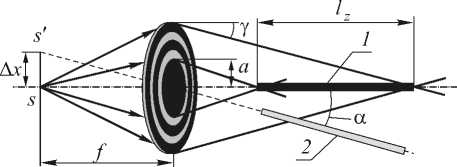
Рис. 1. Схема формирования дифракционно-ограниченного волнового пучка

Здесь: f – расстояние от ДЭ до точечного источника излучения S , 1 – область повышенной концентрации энергии, 2 – положение области повышенной концентрации энергии при смещении точечного источника излучения S от оптической оси в точку S ’. Остальные обозначения ясны из текста.

В зависимости от типа фокусирующего элемента границы зон на его поверхности могут быть рассчитаны различными способами. Например, при осевом точечном источнике излучения в приближении геометрической оптики легко получить, что

F ² + r k + r_ksin y = V F ² + a ² + a sin Y + к X , (1) где k =1,2,_, N , r _N = D /2, у - угол, под которым лучи пересекают оптическую ось, a – опорный радиус [6].

- F 2 ² + a^г a ^- r k

-

кX

В параксиальном приближении отсюда следует, что k^

Y ^ (—).                            (2)

rk

То есть изменение угла падения излучения на оптическую ось элемента происходит линейно от длины волны излучения.

Изучение особенностей дифракции скалярных волн на рассматриваемом дифракционном элементе проводилось методом вычислительного эксперимента [7] на основе строгого вычисления дифракционного интеграла Френеля-Кирхгофа [8]. Были выбраны следующие параметры дифракционного элемента: длина волны – 0.5 мм, диаметр – 15мм, расстояние от плоскости дифракционного элемента до осевого точечного источника излучения – 50 мм, угол падения излучения у =0,153 радиан, а =0. Для корректности применения скалярного приближения при моделировании дифракции на кольцевых отверстиях, ширина которых сравнима с длиной волны излучения, использовался принцип дополнительных экранов, а расчет дифракции велся не для колец, а для отверстий. Это увеличивало время счета, но по-

зволило получить достоверные результаты [7]. Отметим, что при указанных параметрах дифракционного элемента количество зон, укладывающихся на его апертуре, было равно 3, что существенно при рассмотрении дифракционных явлений на «малозонных» элементах [9].

Результаты вычислительных экспериментов

На рис.2б показано распределение интенсивности поля вдоль оптической оси (форма волнового пучка) для дифракционного элемента при исходных параметрах. Амплитудная маска ДЭ приведена на рис. 2 вверху. Смещение положения источника излучения S поперек оптической оси на расстояние A x приводит к отклонению ДОВП (рис. 1). На рис. 2а показана форма волнового пучка при смещенном ( A x =D/3) от оптической оси точечном источнике излучения и при измененной на –5% длине волны излучения. А на рис. 2в – аналогичное рис .2а распределение интенсивности поля, но при измененной на +10% длине волны излучения.

Изменение длины волны излучения от расчетной, как это легко видеть, приводит к изменению протяженности области с повышенной концентрацией энергии. Из (1) и (2) легко оценить, что в параксиальном приближении протяженность области повышенной концентрации энергии обратно пропорциональна длине волны излучения:

, D   (2X. N)

L « —ctg I    1I ®, z 2   ( D J

Здесь X 1 - длина волны падающего на дифракционный элемент излучения, N – число зон Френеля на апертуре ДОЭ и D – его диаметр. В (3) для простоты изложения принято, что опорный радиус [6] равен нулю. Следовательно, регулируя длину волны излучения можно корректировать протяженность области повышенной концентрации энергии, что и наблюдается на рис. 2.

Изучение распределений интенсивности поля поперек отрезка фокусировки при измененных длинах волн точечного источника излучения и его смещении поперек оптической оси показало, что представленные в безразмерном виде эти характеристики практически совпадают между собой.

Отметим, что аналогичными фокусирующими и сканирующими свойствами обладает и одномерный вариант [10] рассмотренного дифракционного элемента.

Таким образом, в работе показано, что дифракционный элемент, формирующий дифракционноограниченный волновой пучок от точечного источника излучения сохраняет свои фокусирующие свойства как при смещении точечного источника излучения от оптической оси, так и при изменении длины волны излучения от расчетной в широких пределах. Указанные закономерности могут найти широкое применение в различных сканирующих системах, в том числе устройствах трехмерного видения [7].