Скейлинг разнообразия в нейтральном сообществе, моделируемом в непрерывном пространстве
Автор: Якимов Василий Николаевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Общие проблемы экологии
Статья в выпуске: 5 т.16, 2014 года.
Бесплатный доступ
В статье представлена модель нейтрального сообщества в непрерывном пространстве и проведен анализ ее пространственной структуры, а именно скейлинга разнообразия, с применением мультифрактального анализа.
Нейтральная теория, моделирование, мультифрактальный анализ, пространственная структура сообщества
Короткий адрес: https://sciup.org/148203306
IDR: 148203306 | УДК: 574.47
Текст научной статьи Скейлинг разнообразия в нейтральном сообществе, моделируемом в непрерывном пространстве
Одним из классов имитационных моделей, получившим в последние годы широкое распространение для описания динамики популяций и сообществ, являются так называемые модели на основе отдельных организмов (individual-based models). Их отличительной особенностью является то, что моделируется поведение отдельных особей, которые могут обладать одинаковыми либо разными свойствами в зависимости от типа модели, при этом особи с разными свойствами обычно составляют популяции разных видов. Такого рода модели представляют значительную трудность в реализации в связи с огромным объемом вычислительных операций, необходимых для проведения симуляций. Именно поэтому их широкое внедрение стало возможным лишь с развитием вычислительной техники [14].
С достаточной долей условности модели на основе отдельных организмов можно разделить на два класса: модели с пространственной структурой и без таковой. В моделях без пространственной структуры сообщество представляет собой панмиктический набор особей, их встречи и взаимодействие носят случайный характер. Напротив, модели с пространственной структурой подразумевают распределение особей по некоторому носителю, например по отдельным обособленным местообитаниям внутри сообщества.
В свою очередь, пространственная структура может быть описана дискретным либо непрерывным образом. При дискретном подходе сообщество моделируется в виде решетки, отдельные ячейки которой соответствуют местообитаниям. Внутри этих ячеек-местообитаний располагаются особи, которые по определенным правилам взаимодействуют, гибнут, размножаются и распространяются по решетке. Непрерывный же подход подразумевает распределение особей в пространстве без каких-либо ограничений, в этом случае
положение особей описывается непрерывными координатами.
Дискретные модели удобны в плане минимизации необходимых вычислительных мощностей и проработанности решеточных моделей в рамках теории перколяции. Континуальные же модели могут претендовать на более полное соответствие реальным сообществам (где особи распределены непрерывно), однако же не получили широкого распространения вследствие вычислительной сложности.
Модели на основе отдельных организмов чаще всего используются для исследования взаимодействия двух (редко – больше) популяций по определенной схеме, например «хищник-жертва». Модели же целых сообществ организмов стали появляться относительно недавно в первую очередь в рамках так называемой нейтральной теории [3, 16, 20]. Однако подавляющее большинство моделей либо не имеют пространственной структуры совсем, либо их пространственная структура дискретна [9, 10, 19].
В настоящем исследовании представлена модель нейтрального сообщества в непрерывном пространстве и проведен анализ ее пространственной структуры, а именно скейлинга разнообразия, с применением мультифрактального анализа. Аналогичный анализ ранее был успешно применен для описания структуры нейтрального сообщества в дискретном пространстве [23].
ОБЩАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВУЮЩИХ ПОПУЛЯЦИЙ В НЕПРЕРЫВНОМ ПРОСТРАНСТВЕ
Рассмотрим непрерывную модель взаимодействующих популяций, впервые предложенную в работе Б. Болкера и С. Пакалы [7] и получившую развитие в работах Р. Ло и У. Дикмана [17, 18]. В наиболее общем виде сообщество состоит из популяций n видов, особи располагаются в большом непрерывном двумерном пространстве (при моделировании – квадрат). Отдельные организмы, располагающиеся в точках x = x,, x2 ^, описываются дельта-функцией Дирака:
5x . ( x )
oo, x = x ’;
0, x x ’.
Распределение в пространстве особей вида i задается функцией pi(x), которая представляет собой сумму дельта-функций отдельных организмов. Интегрирование этой функции по некоторой площади даст число организмов, на ней располагающихся.
В модели фигурируют три процесса: гибель, размножение и перемещение особей. Перемещение описывается как вероятность переместиться из точки x в точку x’ :
Mz(x, x ’) = mt ( x - x) .
Функция m i зависит только от индивидуальных характеристик вида и от расстояния между точками.
Организм вида i , находящийся в точке x , имеет вероятность гибели
D i (x ) = d i + У d j w j )( x-x ')x p j ( x ')- 8ах8х ( x ') ^':
Первый член – параметр d i – это видовой параметр независимой от плотности смертности. Выражение под знаком суммы описывает, как смертность особей вида i зависит от присутствия в окружении особей вида j . Функция w (dd ) ( x — x ’) определяет силу влияния организма вида j , располагающегося в точке x’ , на организм вида i в зависимости от расстояния (индекс d обозначает принадлежность этой функции к смертности). Значение этой функции умножается на плотность вида j в точке x’ p1 ( x ’) . Интегрирование позволяет учесть влияние каждой особи на каждую, проинтегрированное выражение домножается на параметр d ij , определяющий видоспецифичность взаимодействия. При интегрировании необходимо исключить влияние особи саму на себя, для этого в подынтегральное выражение вводится дельта-функция Кронекера:
[ 1, i- j ; ' [0, t^j .
Организм вида i , находящийся в точке x , имеет вероятность произвести потомка в точке x’
B
i
(x
) = |
b
i + ^
|
j
w
j)
)(
x -x")
x
P
j
(
x
") -
По структуре это выражение аналогично выражению для смертности. bi и bij – параметры плотность-независимой и зависимой рождаемости, w(bb)(x — xf) - определяет силу взаимодействия в зависимости от расстояния (индекс b обозначает принадлежность функции к рождаемости). Главное отличие – присутствие дополнительного члена m(b)(x — x’), определяющего пе- ремещение потомка относительно родителя в процессе рождения (в данном случае индекс b также указывает на принадлежность процесса перемещения к моменту рождения).
В качестве функций mt ( x — x ’) , w ( d ) ( x — x ’) , w (bb ) ( x — x ’) и m( b ) ( x — x ’) удобно использовать функции двумерного нормального распределения с нулевым средним. Тогда вид этих функций задается одним параметром – дисперсией распределения.
Сообщество моделируется в непрерывном времени. Для этого используется так называемый алгоритм Джиллеспи [13]. Этот алгоритм был предложен для стохастического моделирования химических реакций. В данном случае его суть сводится к следующему:
-
1. Для каждой особи вычисляются вероятности событий (перемещение – M ,
-
2. Вычисляется сумма этих вероятностей a 0 .
-
3. Выбирается временной интервал dt до следующего события из экспоненциального распределения с параметром a0 : dt= ” ln(1 ~ rnd ) , a 0
-
4. Пропорционально вероятностям случайным образом выбирается и осуществляется событие, например гибель конкретной особи.
гибель – D , размножение – B ).
где rnd – случайное число, равномерно распределенное на интервале (0, 1).
МОДЕЛЬ НЕЙТРАЛЬНОГО СООБЩЕСТВА В НЕПРЕРЫВНОМ ПРОСТРАНСТВЕ
Описанная модель соответствует наиболее общему случаю. При моделировании конкретных сообществ модель существенно упрощается. Так, при моделировании сообщества прикрепленных организмов (например, леса) можно предположить отсутствие перемещений особей (перемещение происходит только в процессе рождения новой особи), то есть m i ( x — x ’) = 0 . Также в первом приближении можно предположить отсутствие влияния локальной плотности на рождаемость, то есть b ij = 0 . Тогда сообщество описывается векторами видовых параметров смертности и рождаемости { d i } и { b i }, вектором стандартных отклонений функции распространения, а также матрицей взаимодействия { d ij } и матрицей стандартных отклонений функции w (dd ) ( x — x f) .
Главным предположением нейтральной теории является идентичность индивидуальных демографических параметров особей. Все особи независимо от видовой принадлежности обладают одинаковыми параметрами рождаемости и смертности (зависимой и независимой от плотности). Тогда для описания сообщества достаточно всего лишь 4 параметров: b (рождаемость), d (не зависящая от плотности смертность), d’ (плот-ность-зависимая смертность), sm (стандартное отклонение для функции распространения) и sw (стандартное отклонение для функции взаимодействия). Для поддержания видового богатства нейтрального сообщества необходимо внести элемент видообразования, иначе, в конце концов, в сообществе останется единственный вид (произойдет фиксация). В рамках существующей нейтральной теории рассматривается два варианта видообразования [11, 16]: точечные мутации (при рождении новой особи существует вероятность υ того, что произойдет макромутация и новая особь будет принадлежать новому виду) и случайное разделение вида (в каждый момент времени существует вероятность того, что вид дивергирует, при этом соотношение численности дочерних видов выбирается случайным образом). Второй вариант никогда не используется в пространственных моделях, поскольку сложно задать универсальный алгоритм расположения особей дочерних видов (случайное разделение имитирует аллопатрическое видообразование, поэтому необходим реалистичный выбор видов для дивергенции и правило для их пространственного разделения). В предлагаемой модели мы следуем этой традиции и используем механизм видообразования путем точечных мутаций.
Исходная модель Б. Болкера и С. Пакалы была предложена для случая двумерного пространства. Нейтральное сообщество также может моделироваться в двумерном пространстве. Тем не менее, в настоящей работе представлены результаты мо- делирования в одномерном пространстве (особи располагаются на отрезке (0, L)). Скорость вычислений при моделировании определяется числом особей, которое растет как квадрат линейных размеров сообщества L в двумерном случае и пропорционально L в одномерном случае. Поэтому в целях ускорения вычислений и возможности работы с более крупными пространственными масштабами мы используем одномерное пространство. Представленные в настоящей работе закономерности пространственной структуры присутствуют и в двумерных реализациях.
Набор параметров, который мы использовали, представлен в таблице. Мы подобрали и зафиксировали параметры рождаемости и смертности ( b , d , d' и s w ) таким образом, чтобы для разных дистанций распространения ( s m ) формировались принципиально различные типы пространственного размещения особей: чем ниже дистанция распространения, тем более агрегированный характер размещения особей отдельного вида мы получаем. Ни скорость видообразования, ни дистанция распространения практически не влияют на плотность особей, которая для данного набора параметров составляет около 2000 особей на единицу линейного пространства. Мы использовали замкнутые граничные условия, то есть особи, располагающиеся у левой границы сообщества, соседствуют с особями на правой границе сообщества.
Таблица. Параметры нейтральной модели
|
Параметр |
Значение |
|
Линейный размер сообщества |
L = 8 |
|
Скорость видообразования |
υ = {0.1, 0.03, 0.01, 0.03, 0.001} |
|
Рождаемость |
b = 0.4 |
|
Независимая от плотности смертность |
d = 0.2 |
|
Зависимая от плотности смертность |
d' = 0.0001 |
|
Стандартное отклонение функции взаимодействия |
s w = 0.12 |
|
Стандартное отклонение функции распространения |
s m = {0.005, 0.01, 0.02, 0.04, 0.08, 0.16} |
В нашей реализации динамика сообщества моделируется вперед во времени: выбирается начальное состояние, рассчитываются вероятности событий и они последовательно реализуются в соответствии с алгоритмом Джиллеспи. В качестве начальных условий мы всегда использовали равномерное распределение 16000 особей по отрезку. По прошествии некоторого времени сообщество приходит к стационарному режиму. Ввиду стохастической природы модели сформировать однозначный критерий выхода на стационарный режим проблематично, поэтому мы использовали следующую стратегию: для каждого набора параметров выбирались контрастные начальные условия (низкое либо высокое видовое богатство относительно стационарного уровня) и отслеживалась динамика трех основных параметров сообщества (общего числа особей N , видового богатства S и индекса видового разнообразия
Шеннона H ), режим рассматривался как стационарный, когда все три параметра для контрастных начальных условий начинали варьировать в одном и том же диапазоне. Типичный пример динамики двух реализаций сообщества представлен на рис. 1. Начальные условия для первой представляют собой 25 видов по 640 особей, случайно равномерно распределенных по отрезку, для второй – 250 видов по 64 особи. После небольшого начального всплеска общая численность особей в сообществах быстро приходит к среднему значению около 15900 особей, общее видовое богатство приходит к стационарному уровню в 130 видов существенно позже (примерно в момент времени 2000), еще медленнее (примерно к моменту времени 4000) устанавливается стационарное значение индекса Шеннона около 4,07. Расчет показателей структуры сообщества производился после выхода на стационарный режим.
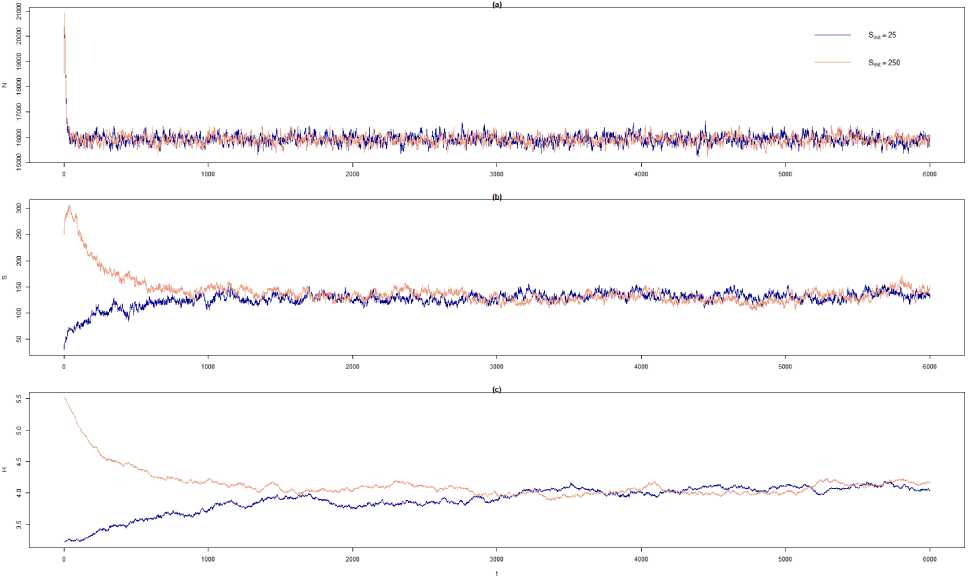
Рис. 1. Динамика двух реализаций нейтральной модели с параметрами υ = 0,001 и sm = 0,005 и контрастными начальными условиями (исходное видовое богатство 25 и 250 видов). (a) Динамика числа особей, (b) динамика видового богатства, (c) динамика индекса Шеннона. По оси ординат отложено модельное время
МУЛЬТИФРАКТАЛЬНЫЙ АНАЛИЗ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ НЕЙТРАЛЬНОГО СООБЩЕСТВА
Наиболее распространенным средством изучения пространственной структуры сообщества является зависимость видового богатства от площади (species-area relationship, SAR), истоки изучения которой восходят к середине XIX в. и трудам Уотсона [2]. Эта зависимость описывает характер роста числа обнаруженных видов при увеличении выборочной площади. Среди большого разнообразия математических моделей, применяемых для описания SAR [21, 22], наибольшим доверием исследователей пользуется степенная модель [5]: S cAz .
Применение степенной SAR эквивалентно фрактальному анализу пространственной структуры сообщества [2, 15]. Особенностью базового фрактального анализа является то, что он не принимает во внимание гетерогенность изучаемого объекта. При построении SAR учитывается только факт присутствия видов на пробных площадях и игнорируется информация об их представлен-ностях: сильные доминанты и редкие виды вносят одинаковый вклад в видовое богатство. Обобщением такого простого подхода является мультиф-рактальный анализ пространственной структуры сообщества. Подробное описание мультифрак-тального анализа, адаптированного для случая анализа структуры сообществ можно найти в работах [1, 2, 4, 8].
Три ключевых этапа мультифрактального анализа: (1) расчет моментов распределения особей по видам для площадок разной площади и выяс- нение характера их зависимости от площади:
S
M q ( A ) =z p iq , i 1
(
где pi – относительная представленность i-го вида, S – общее число видов, обнаруженных на участке площадью A, q – порядок момента. (2) Муль-тифрактальный объект характеризуется степен- ным скейлингом моментов, который описывается так называемыми показателями массы τ(q):
(
M q ( A ) ос A ( q ) .
-
(3) Продуктом мультифрактального анализа явля-
- ется мультифрактальный спектр, получаемый преобразованием Лежандра функции τ(q) [12]:
aq d-т q dq faq qa q^т q
.
(
В основе интерпретации мультифрактального спектра лежат представления о сообществе как о множестве, состоящем из групп видов разных представленностей. В нем можно выделить подмножества видов со сходной представленностью, например группа доминантов, группа субдоминантов, группа редких видов. Степень представленности этих видов характеризует показатель a (обычно называемый индексом сингулярности), отложенный на мультифрактальном спектре по оси абсцисс. По оси ординат на спектре отложены значения фрактальной размерности соответств-
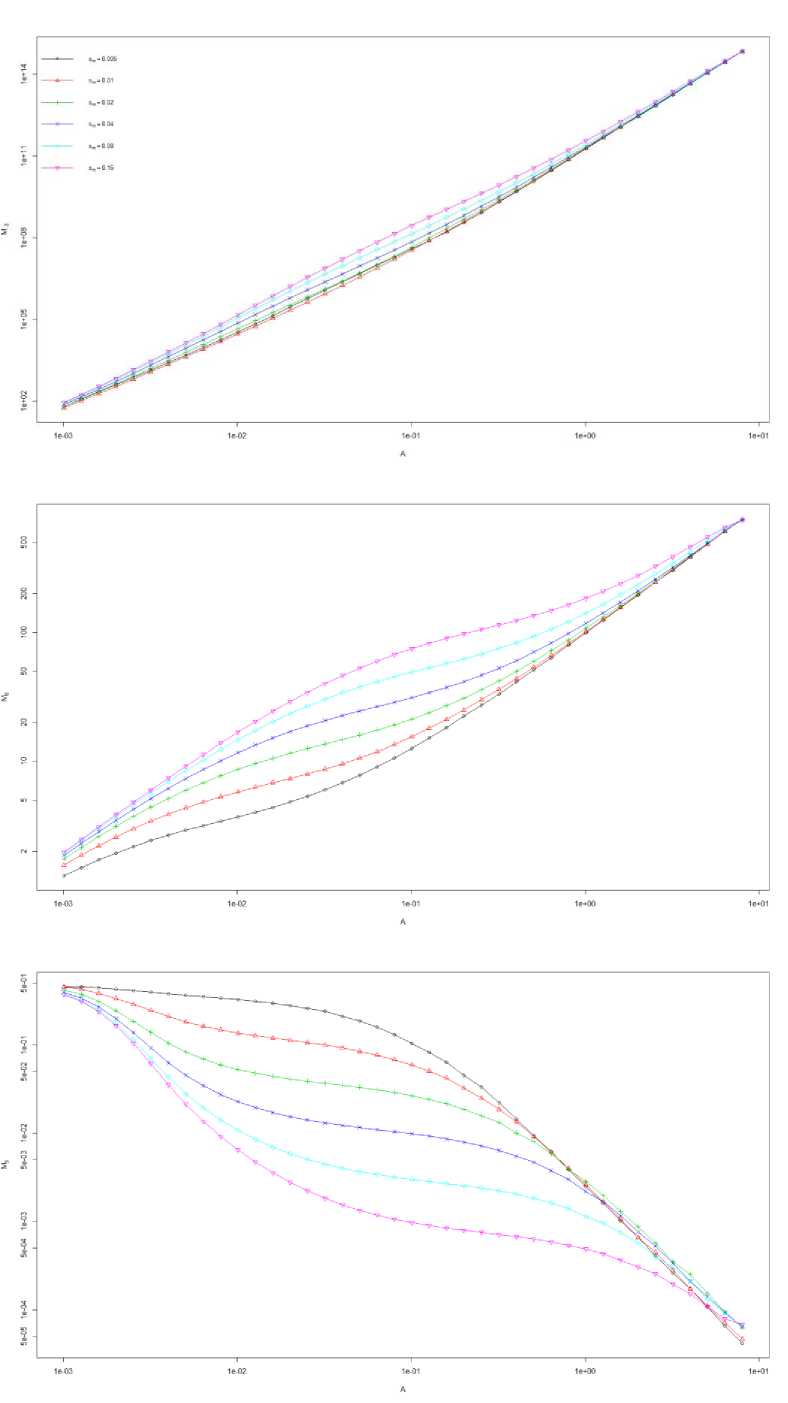
Рис. 2. Зависимость моментов распределения видов по численности M q от площади A в нейтральной модели со скоростью видообразования υ = 0.01. (а) Момент M-3, (b) момент M0 (эквивалентен видовому богатству S), (c) момент M3
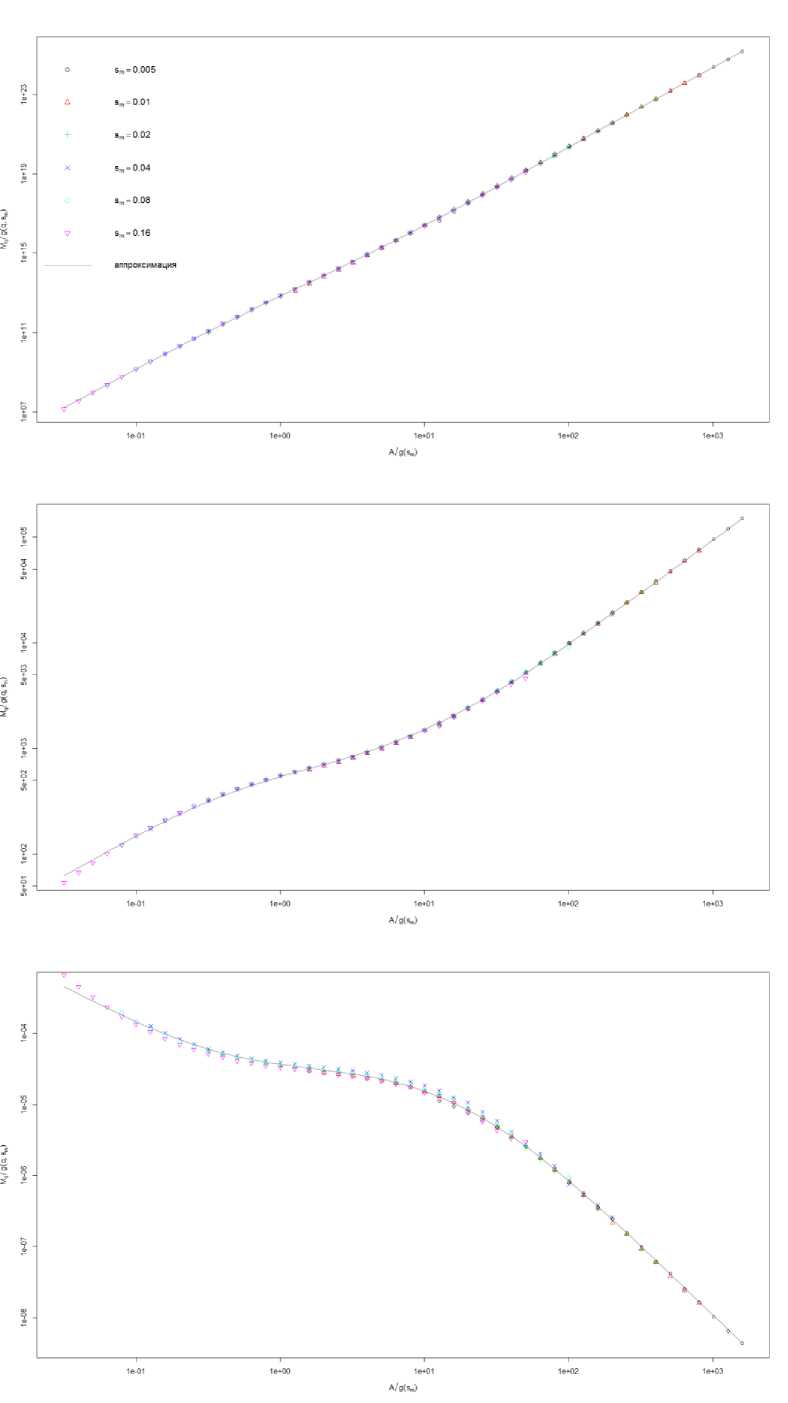
Рис. 3. Универсальные кривые скейлинга моментов M -3 (a), M 0 (b) и M 3 (с) для нейтрального сообщества со скоростью видообразования ν = 0.01 (те же данные, что на рис. 1)
ующих подмножеств, которые интерпретируются как уровень разнообразия в той или иной группе.
Наличие на графике спектра точек, лежащих по оси « a » близко к нулю, означает присутствие в сообществе сильных доминантов (причем, чем меньше абсцисса точек, тем сильнее доминирование); наличие же точек, лежащих близко к единице, означает присутствие в сообществе редких
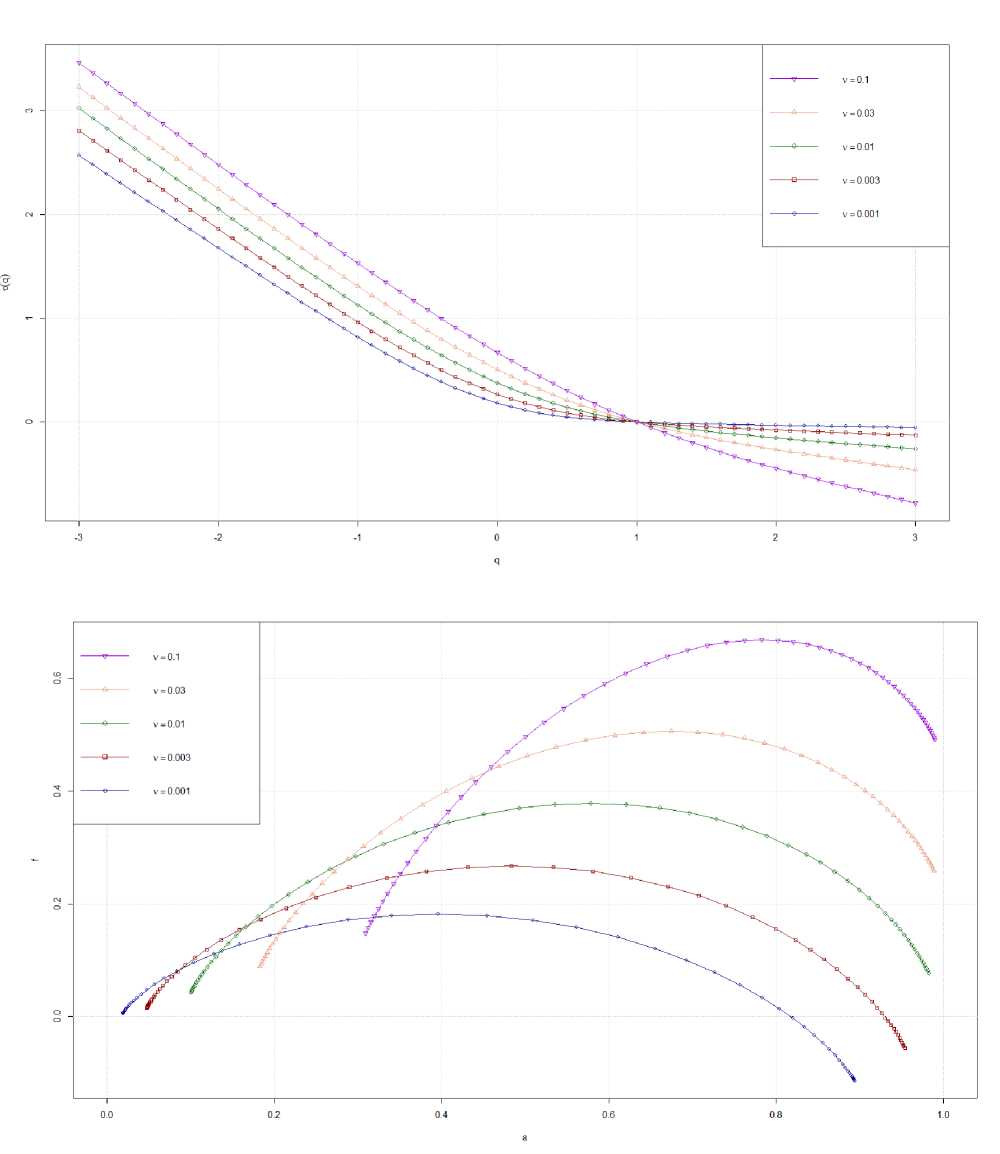
Рис. 4. Результаты мультифрактального анализа пространственной структуры нейтральных сообществ с различными скоростями видообразования для центрального региона скейлинга. (a) Спектры показателей массы, (b) мультифрактальные спектры
видов. Высота спектра характеризует видовое разнообразие в различных группах видов. Расстояние между крайними точками спектра можно интерпретировать как показатель, обратно пропорциональный выровненности видов в сообществе: чем она больше, тем меньше выровнен-ность, и наоборот [2].
Зависимости моментов Mq от площади для со- представлены на рис. 2. Моменты порядков q < 1
общества со скоростью видообразования υ = 0,01 растут с ростом площади, моменты порядков q >
-
1 уменьшаются. При этом зависимости для сообществ с разными дистанциями распространения s m формируют семейства трехфазных кривых, сходящихся на малых и больших масштабах. Сами кривые в семействах имеют одинаковую форму, но сдвинуты друг относительно друга. Такое поведение моментов позволяет использовать технику рескейлинга осей для получения универсальной формы зависимостей моментов от площади [6, 13]: площадь заменяется на A / g ( s m ), а момент на величину M q / g ( q,s m ). Коэффициенты рескейлинга могут быть определяются путем специальной итерационной процедуры, минимизирующей разброс точек вокруг универсальной кривой.
Универсальные зависимости моментов от площади представлены на рис. 3. На представленных графиках символами обозначены данные для сообществ с разными дистанциями распространения, а сплошной линией - аппроксимация зависимости с помощью сплайна. Кривые скейлинга разных моментов в целом аналогичны: на малых и больших масштабах они имеют степенную форму с показателем степени, равным 1- q , на средних масштабах также имеет место участок промежуточного поведения, центральная часть которого также может быть охарактеризована степенной зависимостью. Степенной скейлинг моментов позволяет применить мультифракталь-ный анализ для описания пространственной структуры сообщества. На малых и больших масштабах ситуация тривиальна: зависимость т ( q ) = 1 - q линейна, что свидетельствует об отсутствии контраста в поведении моментов положительных и отрицательных порядков, характеризующих группировки доминирующих и редких видов. В терминах фрактального анализа такая ситуация соответствует монофрактальному скейлингу.
Наиболее интересен с точки зрения мультиф-рактального анализа пространственной структуры средний участок. Показатели массы т ( q ) были рассчитаны как экстремумы производной сплайновой аппроксимации универсальных кривых скейлинга моментов (минимумы для q < 1 и максимумы для q > 1). Зависимости т ( q ) для различных скоростей видообразования v представлены на рис. 4a. Графики имеют нелинейный вид, свидетельствующий о наличии нетривиальной муль-тифрактальной структуры. Следует отметить, что степень контраста между скейлингом моментов разных порядков (степень отклонения от линейности) зависит от скорости видообразования: чем больше v , тем ближе функция т ( q ) к линейности, соответствующей предельному случаю v = 1 (в этом случае все особи будут принадлежать разным видам и мы получим тривиальный случай полной гомогенности).
Мультифрактальные спектры, полученные преобразование Лежандра (3) функций т(q), представлены на рис. 4b. Все спектры имеют холмообразную форму. В первую очередь обращает на себя внимание положение вершины спектров, которая систематически снижается при уменьшении скорости видообразования ν. Левые восходящие ветви спектров характеризуют группировку доминирующих видов: чем ближе крайняя левая точка спектра к началу координат, тем более выражено доминирование в сообществе, высота ветви, как и в случае с положением вершины, характеризует разнообразие в группе до-минантов. С уменьшением скорости видообразования v на фоне общего снижения разнообразия растет доминирование и левые ветви спектров смещаются вниз и влево, то есть подмножество обильных видов становится все более доминирующим, и при этом уменьшается их количество. Правые нисходящие ветви спектров характеризуют подмножество редких видов: чем ближе по абсциссе правая ветвь к единице, тем более редкие виды встречаются в сообществе, предельным случаем редкости являются синглтоны (виды единичной численности). Положение правой ветви спектров по оси ординат систематически снижается с уменьшением скорости видообразования, что указывает на снижение разнообразия в группе редких видов. Для скоростей видообразования и < 0.01 правые ветви спектров заходят в отрицательную область по ординате, что указывает на то, что видовое богатство в группе наиболее редких видов с ростом площади не растет, а снижается [23]. Правые ветви спектров по оси абсцисс смещаются влево при уменьшении скорости видообразования. Этот эффект практически незаметен для высоких υ, но становится очевиден для и < 0.01. Удаление правых ветвей от единицы по абсциссе свидетельствует о том, что на фоне общего снижения видового богатства снижается также и максимальная редкость видов (исчезают синглтоны). Отметим также систематическое сужение спектров при росте скорости видообразования, что свидетельствует о росте выровненно-сти.
ОБСУЖДЕНИЕ
Моделирование пространственной структуры сообществ представляет собой актуальную задачу теоретической экологии. Описание структуры модельных сообществ, динамика которых основана на тех или иных базовых процессах (рождаемость, смертность, взаимодействия, плот-ность-зависимые эффекты), помогает лучше понять связь между структурой сообществ и факторами, ее определяющими. Наибольший прогресс в данном направлении на сегодняшний день достигнут в рамках нейтральной теории, которую можно рассматривать как базовую для построения более сложных моделей. Тем не менее, даже в рамках нейтральной теории рассматриваются модели, описывающие пространство либо неявным образом (путем разделения на масштабные уровни локальных сообществ и глобального метасообщества), либо дискретно (путем представления пространства в виде решетки соседствующих местообитаний). Однако в реальных сообществах дискретизация пространства отсутствует, положение особей в пространстве описывается непрерывными координатами.
В настоящей работе мы попытались восполнить имеющийся пробел и предложили модель нейтрального сообщества в непрерывном пространстве. Модель основана на базовых процессах рождаемости, смертности, ограничения распространением зависимости от плотности. Для нейтральных моделей с неявным и дискретным моделированием пространства характерны первые три процесса, но отсутствуют плотность-зависимые эффекты. Модель воспроизводит различные степени агрегирования видов: чем меньше дистанция распространения s m , тем выше агрегирование.
Для описания пространственной структуры моделируемых сообществ проведен мультифрак-тальный анализ. Результаты анализа в целом соответствуют таковым для решеточной нейтральной модели [23]. Зависимости моментов распределения видов по численности Mq от площади A в сообществах с разными дистанциями распространения формируют семейства кривых, сходящихся на малых и больших масштабах. Сами кривые при этом имеют одинаковую трехфазную форму, что позволяет получить универсальные кривые скейлинга моментов. На малых и больших масштабах наблюдается тривиальный скейлинг, свидетельствующий о гомогенности распределения, промежуточные же масштабы обладают нетривиальной структурой, которая хорошо описывается мультифрактальными спектрами. Для нейтральной модели в непрерывном пространстве в целом характерны те же тенденции изменения спектров при уменьшении скорости видообразования, что и для модели в дискретном пространстве: вершина спектров опускается, левые восходящие ветви смещаются влево и вниз, правые ветви опускаются. Новый эффект, который отсутствует в дискретном пространстве – это смещение правых ветвей влево, свидетельствующий о падении минимального уровня редкости в промежуточном диапазоне масштабов.
Таким образом, пространственная структура нейтральных сообществ, моделируемых в дискретном и непрерывном пространстве, в значительной степени совпадают на качественном уровне. Выявленные отличия касаются тонких деталей, на которые дискретизация оказывает влияние. Так, в дискретной модели рескейлинг осей для получения универсальной формы зависимости видового богатства от площади перестает работать при дистанциях распространения, сопоставимых с размером ячейки [19]. В непрерыв- ной модели такого рода эффекты не проявляются. Отсутствие в решеточной модели эффекта снижения максимальной редкости при падении скорости видообразования также можно объяснить дискретизацией пространства, которая устанавливает предел локальной плотности особей одного вида, в результате чего при снижении общего видового богатства не проявляется эффект исчезновения синглтонов в средних масштабах.
Полученные нами результаты, с одной стороны, верифицируют адекватность нейтральных моделей в дискретном пространстве для описания основных закономерностей пространственной структуры сообществ, с другой – указывают на те элементы, которые чувствительны к эффекту дискретизации пространства.
Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований (код проекта 14-04-01548).
Список литературы Скейлинг разнообразия в нейтральном сообществе, моделируемом в непрерывном пространстве
- Гелашвили Д.Б., Иудин Д.И., Розенберг Г.С., Якимов В.Н., Солнцев Л.А. Основы мультифрактального анализа видовой структуры сообщества//Успехи соврем. биол. 2008. Т. 128. № 1. С. 21-34.
- Гелашвили Д.Б., Иудин Д.И., Розенберг Г.С., Якимов В.Н., Солнцев Л.А. Фракталы и мультифракталы в биоэкологии: Монография. Нижний Новгород: Изд-во Нижегородского университета, 2013. 370 с.
- Гиляров А.М. В поисках универсальных закономерностей организации сообществ: прогресс на пути нейтрализма//Журн. общ. биол. 2010. Т. 71. С. 386-401.
- Иудин Д.И., Гелашвили Д.Б., Розенберг Г.С. Мультифрактальный анализ структуры биотических сообществ//Докл. РАН. 2003. Т. 389. № 2. С. 279-282.
- Arrhenius O. Species and Area//J. Ecol. 1921. Vol. 9. P. 95-99.
- Bhattacharjee S.M., Seno F. A measure of data collapse for scaling//J. Phys. A: 2001. Vol. 34. P. 6375-6380.
- Bolker B., Pacala S.W. Using Moment Equations to Understand Stochastically Driven Spatial Pattern Formation in Ecological Systems//Theor. Popul. Biol. 1997. Vol. 52. P. 179-197.
- Borda-de-Agua L., Hubbell S.P., McAllister M. Species-Area Curves, Diversity Indices, and Species Abundance Distributions: A Multifractal Analysis//Am. Nat. 2002. Vol. 159. P. 138-155.
- Cencini M., Pigolotti S., Muñoz M.A. What Ecological Factors Shape Species-Area Curves in Neutral Models?//PLoS ONE. 2012. Vol. 7. P. e38232.
- Chave J., Muller-Landau H.C., Levin S.A. Comparing classical community models: theoretical consequences for patterns of diversity//Am. Nat. 2002. Vol. 159. P. 1-23.
- Etienne R.S., Apol M.E.F., Olff H., Weissing F.F. Modes of speciation and the neutral theory of biodiversity//Oikos. 2007. Vol. 116. P. 241-258.
- Evertsz C.J.G., Mandelbrot B.B. Multifractal measures//Chaos and fractals: new frontiers of science (Eds. Peitgen H.-O, Jurgens H., Saupe D.). New York: Springer, 1992. P. 921-953.
- Gillespie D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions//J. Comp. Phys. 1976. Vol. 22. P. 403-434.
- Grimm V., Railsback S.F. Individual-based Modeling and Ecology. Princeton: Princeton Univ. Press, 2005. 480 pp.
- Harte J., Kinzig A., Green J. Self-Similarity in the Distribution and Abundance of Species//Science. 1999. Vol. 284. P. 334-336.
- Hubbell S.P. The unified neutral theory of biodiversity and biogeography. Princeton: Princeton Univ. Press, 2001. 375 pp.
- Law R., Dieckmann U. A dynamical system for neighborhoods in plant communities//Ecology. 2000. Vol. 81. P. 2137-2148.
- Law R., Murrell D.J., Dieckmann U. Population growth in space and time: spatial logistic equations//Ecology. 2003. Vol. 84. P. 252-262.
- Rosindell J., Cornell S.J. Species-area relationships from a spatially explicit neutral model in an infinite landscape//Ecol. Let. 2007. Vol. 10. P. 586-595.
- Rosindell J., Hubbell S.P., Etienne R.S. The Unified Neutral Theory of Biodiversity and Biogeography at Age Ten//Trends Ecol. Evol. 2011. Vol. 26. P. 340-348.
- Tjørve E. Shapes and functions of species-area curves: a review of possible models//J. Biogeogr. 2003. Vol. 30. P. 827-835.
- Tjørve E. Shapes and functions of species-area curves (II): a review of new models and parameterizations//J. Biogeogr. 2009. Vol. 36. P. 1435-1445.
- Yakimov B.N., Iudin D.I., Solntsev L.A., Gelashvili D.B. Multifractal analysis of neutral community spatial structure//J. Theor. Biol. 2014. Vol. 343. P. 44-53.


