Скорости фильтрации в области отжима материалов

Автор: Ш. Р. Хуррамов

Журнал: Современные инновации, системы и технологии.

Рубрика: Машиностроение, металлургия и материаловедение

Статья в выпуске: 2 (4), 2022 года.

Бесплатный доступ

Определены аналитические зависимости, описывающие закономерности изменения скоростей фильтрации в области отжима. Установлено, что скорость фильтрации жидкости вдоль оси абсцисс на границах зоны сжатия равна нулю, а внутри зоны принимает отрицательные значения. Выявлено, что скорости фильтрации жидкости вдоль оси ординат и полярного угла равны нулю в начале зоны сжатия, возрастают до максимума в одной точке, лежащей на линии центров, а в зоне восстановления деформации зависят от угла, определяющего положение точки, где жидкость меняет направление.

Валковый отжим, мокрый материал, гидравлические задачи, фильтрация, скорость фильтрации

Короткий адрес: https://sciup.org/14124568

IDR: 14124568 | DOI: 10.47813/2782-2818-2022-2-4-0312-0323

Текст статьи Скорости фильтрации в области отжима материалов

DOI:

В процессе валкового отжима мокрых материалов наблюдается одновременное происхождение двух явлений ‒ контактное взаимодействие и фильтрация влаги. Это, в свою очередь, требует совместного решения при этом двух типов задач ‒ контактных задач и гидравлических задач.

В работах [1-4] были решены основные контактные задачи валкового отжима мокрых материалов.

Основными гидравлическими задачами валкового отжима мокрых материалов являются задачи аналитического описания распределения гидравлического давления и математического моделирования остаточной влажности отжимаемого материала. Для решения этих задач необходимо знать закономерности изменения скоростей фильтрации в области отжима.

Анализ работ, посвященных исследованию гидравлических задач валкового отжима мокрых материалов [5-11], показал, что существующие закономерности изменения скоростей фильтрации в области отжима получены с введением моделей валкового оборудования и материалов, не отвечающих реальным физическим явлениям валкового отжима мокрых материалов. Поэтому они не дают возможности по решению задач, позволяющих полностью раскрыть гидравлические явления валкового отжима мокрых материалов.

МАТЕРИАЛЫ И МЕТОДЫ

В работе [12] были определены аналитические зависимости, описывающие закономерности изменения скоростей фильтрации в области отжима для симметричного двухвалкового модуля. В целях дальнейшего развития теоретических представлений, как и в работах [1-4], объектом исследования служит обобщенный двухвалковый модуль, в котором валки расположены относительно вертикали с наклоном справа под углом β , имеют неравные диаметры с эластичными покрытиями ( D_x ^ D ₂), слой мокрого (обрабатываемого) материала имеет равномерную толщину δ и подается наклоном вниз относительно линии центров под углом γ (рисунок 1).

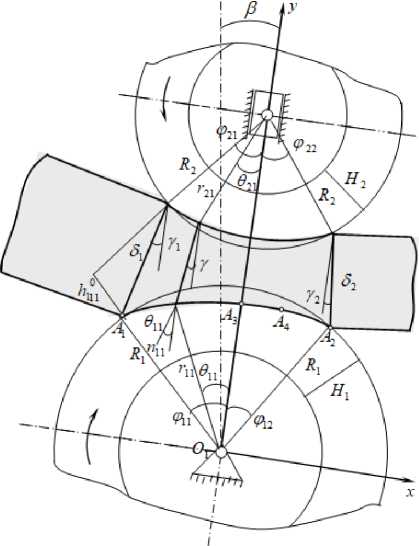
Рисунок 1. Схема двухвалкового модуля.

Figure 1. Scheme of a two-roll module.

Кривая контакта нижнего валка (кривая A 1 A 2 ) состоит из двух зон A A и A A . В зоне A A происходит сжатие слоя мокрого материала и покрытия валка, а A A – восстановление деформации.

Сначала рассмотрим процесс фильтрации жидкости в зоне A A . В этой зоне обрабатываемый материал сжимается, поэтому жидкость переходит из нее в покрытие валка вдоль полярного угла [5].

Скорость мокрого материала в области контакта величина постоянная и равна v_m .

Скорость жидкости в области контакта величина переменная и равна сумме двух составляющих [12]:

^£ 11 ^У 11жх = ^£ 11 v m + u 11 x , ^ 11 ^V 11жy = u 11 y , ⁽¹⁾

где Vixx> Vnжу - абсолютная скорость жидкости в зоне AXA3 вдоль оси Ox и Oy, соответственно; vnх, vn— относительная скорость жидкости в зоне AXA3 вдоль оси Ox и Oy, соответственно; uxxх, ихху — скорость фильтрации жидкости в зоне AXA3 вдоль оси Ox и Oy , соответственно; ε - относительная деформация мокрого материала в зоне A A .

В процессе фильтрации для скоростей v и v должно выполняться уравнение неразрывности [12]:

∂ ( ε ₁₁ v_m + u ₁₁ _x ) ∂ ( u 11y )

∂x11 ∂y11

Отсюда находим

∂ ε ₁₁ ∂ u ₁₁ _x ∂ u 11y = 0.

∂x ∂x∂

Переходим к дифференцированию по одной переменной θ + γ :

d ε ₁₁ d ( θ ₁₁ + γ ) du ₁₁ _x d ( θ ₁₁ + γ ) du 11y d ( θ ₁₁ + γ )

v ⋅ + ⋅ + ⋅=

d(θ +γ) dx d(θ +γ) dx d(θ +γ)

После преобразования получим

du ₁₁ _y	dy ₁₁		du ₁₁ _x	dy ₁₁
du ₁₁ _y	d ε ₁₁	d ( θ 11 + γ )	du ₁₁ _x	d ( θ 11 + γ ) = 0.	(3)
=		dx ₁₁		d ( θ 11 + γ ) = 0.	(3)
d ( θ 11 + γ )	^- ^vm d ( θ 11 + γ ) ^⋅	dx ₁₁	d ( θ 11 + γ )	dx ₁₁
		d ( θ 11 + γ )		d ( θ 11 + γ )
Заметим, что	u ₁₁ _y	= u ₁₁ _xctg ( θ ₁₁	+ γ ) .		(4)

Проведем дифференцирование du11y du1

= 11x ctg (θ + γ) - u.

d ( θ 11 + γ ) d ( θ 11 + γ ) ^{11 11} ^x sin ² ( θ 11 + γ )

Учитывая это, из равенства (3) получим

dx ₁₁ dy ₁₁	dy ₁₁
cos( θ ₁₁ + γ ) + sin( θ ₁₁ + γ )	dy ₁₁
d ( θ ₁₁ + γ ) d ( θ ₁₁ + γ ) du ₁₁ _x 1 d ε 11	d ( θ 11 + γ ) _dx . (6)
dx 11 _sin( θ ₊ γ ₎ d ( θ ₁₁ + γ ) sin ² ( θ ₁₁ + γ ) ¹¹ ^x ^md ( θ ₁₁ + γ )	d ( θ 11 + γ ) _dx . (6)
d ( θ 11 + γ ) ¹¹	d ( θ 11 + γ )

Из рисунка 1 следует, что x11=r11sin(θ11+λ), y11 = r11 cos(θ11 +γ).

Отсюда находим

——^ = rX1 ^sin(^ 1 ⁺ Y ) ⁺ r ii ^cos( ⁰ ii ⁺ Y ), d ( 9 ii + Y )

11 . = r i ' i ^cos ( ⁰ ii ⁺ Y ) - r ii ^sin( ⁰ ii ⁺ Y )

d ( 9 ii + Y )

Подставляя эти производные в равенства (6) и считая rx‘ sin 2 (0, + у) * 0, после несложных преобразований находим

1 du _nx u _nx r i ' i^cos( ^ ii ⁺ Y ) ^- r ii^sin( ⁰ ii ⁺ Y ) ^dew

----------------------------------* ---;-------------= V^ -----------------------------------------------*---------------. ^cos( ⁰ ii ⁺ Y ^)sin( ⁰ ii ⁺ Y ) ^d ⁽ ⁰ ii ⁺ Y ) ^{sin (} ⁰ ii ⁺ Y ) r i ' i^sin( ⁰ ii ⁺ Y ) ⁺ r ii^cos( ⁰ ii ⁺ Y ) ^d( 9 ii ⁺ Y )

Уравнение кривой контакта нижнего валка в зоне сжатия для рассматриваемого двухвалкового модуля имеет вид [2]:

где

r ii =

^R f i + k, _A1 *⁺ ^Y - > )

1 + k 1 A I cos( 0 _n + Y ) J

^- ⁽ Ф 11 + Y i ) ^ ⁰ ii + Y ^ °,

К _ miiHisin^ii + Ф21) , k ii = *$•„•/„ t , A1 = mi ^sin Ф21 - Yi)

A ii m ii ( A l ii ) ср - ( A ii (i - m _n) - A _n(i - m _n)) ^ 0

^A 11 m 11⁽ ^A l ii ) ср ⁺ ⁽ A ii⁽ⁱ - m ii ) - A ii⁽ⁱ - m ii ))^H i

h i°i = . 1^ ⁱⁿ ( ^Ф 2L - ^Y LL ; ( A I n) _cp = R i .f i - sn ^ii ⁺ ^Y i ) )

sin ⁽ Фи ⁺ ф ₂1) ( 2 ⁽ Ф _П ⁺ Y i ) J

здесь m_x , - коэффициент упрочнения точек эластичного покрытия нижнего валка при сжатии, m * - коэффициент упрочнения точек волокнистого материла при сжатии.

Откуда

== ^k„А , R * ^cos( H . ⁺ ^Y ⁾ tg(_6ii + Y ). + k_xAi cos ф ( ^ ! + y )

Используя выражение (8) и (9), имеем

^r 'i sin ^ i i ⁺ Y ) ⁺ r i i ^cos( 6 ,i i ⁺ Y ) =

R_x k_x A n cos( ф l + Y i) + cos³( # n + y )

1 + k_x A n cos²( 0 _n + y )

r ‘ i c ^os( y i i + y ) ^- r i i SinC ^ i + y ) = ^- ¹ si ⁿ⁽ 6 >i i + y ) .

⁺ k i ^A i

После подстановки этих выражений и некоторых преобразований уравнение (7)

принимает вид

1 du,, u,, x x

----------------------------------------------------------------------------------*---------------------------------- cos(^ii + Y)sin(^ii + Y) d(9ii + Y) sin (9ii + Y)

—

sin( ^ , + y )cos 2 ( ^ ! + Y ) d ^ i

------------------------------------------------------------------------------------------------------------------------------------------*---------------------------------------

⁽ k_п^A _пc^os( ф _п ⁺ Y i ) + ^cos ( 0 11 ⁺ Y )) d (0 11 ⁺ Y )

. (11)

Из рисунка 1 следует, что

Откуда

^s 11 ^—

^cos( ^ _n ⁺ Y 1 ) ^{11 1} cos ^ n + у )

_h ₁ 0 ₁

d s _vv _ ^cos^ + y Jsm O + у )

---------------- —--:------------------------:-------------- . d ( On + Y ) h u(1 + k 1 A 1 )cos 2 ( # 11 + у )

Подставим это выражение в равенство (11):

du 11 x cos(°11 + Y) u = d (O11 + Y) sin(O11 + Y) 11 x

v „ ^ 1 Cos ⁽ ^ _n + Y 1 ) sin ³⁽ ^O _n + у ⁾ cos ⁽ ^O _n + у )

• h11(1 + k 11^11) (k 11^11 cos(^n + Y1)+ cos (O11 + Y))

. (14)

Дифференциальное уравнение (14) является линейным. Его однородная часть

имеет решение u 11 x — chOh + Y)sin(O11 + у) , (15)

откуда

„du ¹¹ ^x . ^— „dC ¹¹ . sin ⁽ O ⁺ Y ) ⁺ C 11 cos ⁽ ^O _n ⁺ Y ).

d ⁽ ^O 11 ⁺ Y ) ^d ⁽ ^O 11 ⁺ Y )

Подставив u11x и u в уравнение (14), имеем d O + Y) 11 x

^d C 11 x v m^R 1^cos ( ^ 11 ⁺ Y 1 ) ^s in ² ( ° 11 ⁺ Y ^)cos ( ° 11 ⁺ у )

------------=---------------------•------------------------------------------- .

d ( ° 11 ⁺ Y ) ^h 11⁽¹ ⁺ ^k и ^ и) ( ^k 11 ^ 11 ^co s( ^ 11 ⁺ Y 1 ) ⁺ ^cos ( ° 11 ⁺ Y ))

Введем допущения sin( O , + у ) * O i + Y

^cos(9_u + у ) * ¹ - ⁽ ^O 11 + ^Y ) .

После этого равенство (16) принимает вид

dC 11 _=Q ( O 11 + Y ) 2

d(9_n + Y ) ¹¹ m 2 - ( O n + Y ) 2 ^,

где

2 vR, cos( ^ . + у .) ₂ 2

^ 1₁— — ^m 1 ^{11 1} , m ² — -(1 + k ^! cos( ^ ! + у )).

¹¹ 3 h 0 (1 + k_Y Л J ¹¹ 3 ^{1141 11 1}

Интегрируем равенство (21)

C 11

Г ^— an

(On + ^ ) + m 1¹ ln

mu ⁺ ( ° " ⁺ ^Y ) L C *

m u - ( O 11 + Y ) J ¹¹

Раскладывая логарифмическую функцию в ряд и ограничиваясь членами до третьей степени относительно (O x + у), имеем CY t —

J a ^( O 11 + у ) ³ + C *1 . 3 m ₁ ² ₁

Подставим это выражение в уравнение (15):

u 11 x

ЛЛ Л + y ) ³ + C_n sm( 9 _n + у ) .

( 3 ^т_и )

C *

j j по начальному условию ux ,х (-(^, + у )) = 0, имеем ullx = blM + Yl)3 + (9ll + Y)3)sin(9ll + Y), — (^и + Yl) ^ 9n + у < 0, vrnRlcosCfll+Zl)

где b_ll =

^u 1²1 y ^.

Выражения имеют вид:

u12 x — b12«^14 + Y4)3 - (012 + Y^W0 + Y), 0 - 012 + Y - ^14 + Y4 , u12 y =- b12((^14 + Y 4)3 - (012 + Y )3)cOs(012 + YX 0 - 012 + Y - Ф14 + Y4 , u120 =-b12((^14 + Y4)3 — (012 + Y)3), 0 - 012 + Y - ^14 + Y4 ,

_________ vm^R1 ^COS ( ^ 12 ⁺ Y 2 ) _________ 3 h 0 (1 + k ₂^ ₂ )(1 + k ^ ₂ cos( ^ ₂ + y₂ ))

Авторы работ [8, 9], считают, что на втором участке A A зоны восстановления деформации скорость фильтрации вдоль оси Ox равна нулю, то есть u12ж(02 + y) = 0 , где ^4 + y4 - 02 + Y - ^2 + Y. В этом случае, из равенства, соответствующего (3)

следует, что dy12

du 12 y d £ ₁₂ d ( 0 ₁₂ + Y )

---------- — — V -----------;----- d (012 + Y) md (912 + Y) dX12

d ( 9 12 + Y )

или с учетом аналогичных выражений (9) и (17)

^d u 12 y _ ^Vm R 1^Cos( ^ 12 ⁺ Y 2 ) sin ²⁽ ⁰ 12 + Y )

---------------- —------------------------- • ------------------------------------------ T --------------- .

d ( 0 2 + Y ) h 02 (1 + k ₂ ^ ₂) ( k ₂ ^ ₂ cos( ^ ₂ + y₂ ) + cos ³ ( 0 ₂ + Y ))

Преобразуем с учетом аналогичного выражения (18)

^du 12 y _{= a} ( 0 12 + Y )²

d ( 0 12 + Y ) ¹² m 22 — ( 0 12 + Y ) .

Решение этого уравнения будет

f u 12 y — T1r(012 + Y )3 + C13

( 3 m12

По условию u ₁₂y < ^ ₁₄ + Y ₄ ) — 0 определяем, C *₃ — —a¹²- ( ^ ₁₄ + y ₄ ) ³ .

3 m ₁ ² ₂

После этого получаем u12y — b12((^14 + Y4)3 - (012 + Y)3), ^14 + Y4 - 012 + Y - ^12 +

Отсюда, имеем u120 ——b12((^14 + Y4)3 — (012 + Y)3), ^14 + Y4 - 012 + Y - ^12 +

Обобщая формулы (21), (24) и (27), получаем u110 —— b11((^11 + Y1)3 + (011 + Y)3), —(^11 + Y1) - 011 + Y - 0,

где Ф _Х4 + Y 4 = S 1⁽ V 12 + Y 2 ), ⁰ < S 1 ^- 1.

Скорости фильтрации жидкости, протекшей через кривую контакта верхнего валка, определяем аналогично.

Они имеют вид:

u 21 9 = b 21 (( ^ 21 - ^Y 1 ) 3 ⁺ ⁽ ⁹ 21 - ^Y ) 3 ), - ( ^ 21 - ^Y 1 ) - ⁹ 21 — ^Y ^- 0,

u229 = b22((^24 — Y4) — (922 — Y) )’ 0 — 922 - Y — ^22 - Y2, где ^24 - Y4 = S 2(^22 - Y2), 0 < S 2 - 1, b = __________vmR2 cOs(^22 - Y2)__________

²² 3 h 0₂ (1 + k₂₂^ ₂)(1 + k₂₂^ ₂ cos( ^ ₂ - y₂ ))"

На рисунках 2 и 3 приведены интерпретирующие формулы (11) и (12).

b 21 =

__________ v m^R 2 ^CO s ⁽ ^ 21 - Y 1 ) __________ 3 h 201 (1 + k 2Л1 )(1 + k 2A1 COS( ^ 21 - Y 1 )) ,

графики изменения скоростей фильтрации,

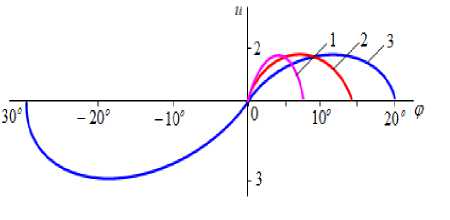
Рисунок 2. График изменения скорости фильтрации :

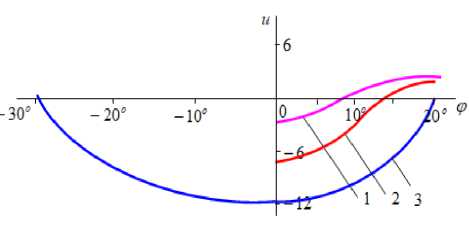
Рисунок 3. График изменения скорости фильтрации нижнего валка:

Figure 2. Graph of the change in speed filtration u :

1 - s = 0,33; 2 - s = 0,67; 3 - s = 1 .

Figure 3. Graph of the change in speed bottom roll filtration:

1 - S = 0,33; 2 - S = 0,67; 3 - S = 1 .

РЕЗУЛЬТАТЫ

1. Определены аналитические зависимости, описывающие закономерности изменения скоростей фильтрации в области отжима.
2. Установлено, что скорость фильтрации жидкости вдоль оси абсцисс на границах зоны сжатия равна нулю, а внутри зоны принимает отрицательные значения.
3. Выявлено, что скорости фильтрации жидкости вдоль оси ординат и полярного угла равны нулю в начале зоны сжатия, возрастают до максимума в особой точке, лежащей на линии центров, а в зоне восстановления деформации зависят от угла, определяющего положение точки, где жидкость меняет направление.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

Из анализа расчетных данных и графиков (рисунки 2 и 3) следует:

• скорость фильтрации жидкости вдоль оси Ox на границах зоны сжатия равна нулю, а внутри зоны принимает отрицательные значения. Она имеет минимум в точке, определяемой углом ϕ = 0,63 ϕ ( ϕ - угол захвата валка);
• закономерности изменения скоростей фильтрации вдоль осей Ox , Oy и угла θ в зоне восстановления зависят от числа ζ , определяющего положение точки, где жидкость меняет направление. Чем ближе ζ к нулю, тем длиннее часть зоны восстановления деформации, где жидкость перемещается из покрытия валка обратно в мокрый материал. По мере увеличения числа ζ от нуля до единицы, протяженность изменения скорости фильтрации вдоль оси Ox увеличивается. При ζ = 1 , скорость фильтрации u внутри зоны восстановления положительна, имеет максимум в точке, определяемой углом ϕ = 0,63 ϕ ( ϕ - угол выхода). При этом она в начале и конце зоны восстановления деформации равна нулю.

Статья