Скрытая передача информационных сигналов на основе модифицированного вейвлет-преобразования

Среди современных информационно-измерительных систем имеется класс распределенных систем, которые обеспечивают сбор, обработку, детектирование и идентификацию определенных ключевых признаков сигнала для селективного распределения информации по узлам сети ЭВМ. Системы этого типа являются носителями потоков сообщений большой интенсивности с высокой значимостью (зависящей от контекста решаемых системой задач). Одновременно они достаточно уязвимы с точки зрения возможного несанкционированного доступа к сообщениям в каналах связи элементов сети (ЭВМ, кабельных прокладок, концентраторов). Наиболее существенна проблема конфиденциальности в информационных системах с речевыми сигналами. В статье рассмотрен метод обеспечения скрытой передачи речевых сигналов в распределенных информационных системах, основанный на использовании скремблирования с двойным преобразованием сигнала.

ПОСТАНОВКА ЗАДАЧИ. ТРАДИЦИОННЫЕ РЕШЕНИЯ

Поскольку в распределенных системах, как правило, необходимо сохранение конфиденциальности информации, а передача ее между узлами системы и хранение в базах данных в открытом виде нарушает требование конфиденциальности, то в этом случае целесообразно применять скремблирование речевого сигнала. Такие системы работают в режиме реального времени, поэтому закрытие информации осуществляется алгоритмом, который не только дает низкую остаточную разборчивость, большое количество ключей, иммунитет к криптоанализу и сохранение качества речи при умеренной сложности алгоритма, но и выполняется достаточно быстро и вносит минимальные задержки при записи и воспроизведении речевого сигнала.

Первый уровень скремблирования (тактический), являющийся защитой от технически невооруженного прослушивания, использует частотную инверсию и частотную инверсию с тональным маскированием. При этом требование минимальности искажений ограничивает число частотных полос и ведет к снижению количества ключей и к большей остаточной разборчивости. Первая из пяти полос, например, содержит около 40 % энергии сигнала и первую форманту, что после тренировки позволяет понимать скремблированную речь [1].

Второй уровень использует частотное скремблирование с методом БПФ, временное и частотновременное скремблирование [2]. Частотное скремблирование с методом БПФ является обобщением метода инверсии, при котором в канал передается временная форма ~ скремблированного сигнала $:

~

$ Fn PnF n$, где Fn — n-точечные преобразования Фурье, Pn _ матрица перестановок.

Метод связан со значительной вычислительной нагрузкой и необходимостью подбора матриц Р_п для обеспечения вещественности скремблированного сигнала ~ . Кроме того, ориентируясь на известную форму спектра речевого сигнала, аналитик имеет возможность с помощью критерия восстановления типичной формы частотного спектра сигнала речи подобрать матрицу перестановок P и восстановить оценку ? с помощью процедуры

~ ^ F • ~ ^ P • F • ~ ^ F P = P ^ч, ? = $ ,

¹ • ^P • ^F • ~ a s ,     (2)

где F — оператор БПФ и F ^-1 — обратная операция, т. е. БПФ^-1.

Метод временного скремблирования обеспечивает несколько большую безопасность, чем метод частотного скремблирования, но включает перестановку временных отсчетов на фрейме сигнала и приводит к высокой задержке.

Модификации с обращением временных сегментов, со скремблированием временных отсчетов или временных элементов, содержащих несколько отсчетов сигнала, также не вполне удовлетворительны. Короткие сегменты (40-100 мс) приводят к большой остаточной разборчивости, а длинные сегменты (300–600 мс) — к значительным задержкам. Кроме того, метод обращения временных сегментов не скрывает гласные фонемы и дает искажения на границах сегментов.

Трудности метода скремблирования временных элементов, основанного на перестановке сегментов внутри фрейма речевого сигнала, связаны с некоторой противоречивостью требований. Лучшую защиту дают короткие сегменты, но это ведет к искажениям сигнала на границах сегментов и расширению частотной полосы сигнала. Компромиссная длительность 16–60 мс позволяет сохранить определенный баланс "качество—безо-пасность", но дает задержку при передаче такую, как у спутниковой связи.

Количество сегментов 8, удобное для аппаратной реализации, дает число ключей всего 40320 (8!), которое еще снижается при отборе перестановок по shift-фактору. Хорошими являются по разным оценкам не более 10 % общего количества перестановок [2, 3]. Кроме того, скремблирование медленно меняющегося сигнала дает невысокий уровень безопасности. В частности, если фрейм равен длительности фонемы, то скремблирование лишь ухудшает качество фонемы, сохраняя ее распознаваемость.

Метод частотно-временнóго скремблирования включает в качестве фаз этап частотного скремблирования и этап перестановок временных отсчетов и некоторым образом объединяет недостатки, свойственные каждому из этапов.

Совершенствование методов скремблирования возможно путем введения новых видов преобразования сигнала, существенно снижающих остаточную разборчивость, значительно повышающих количество ключей и обладающих быстрым алгоритмом реализации. Предложенный в [4], [5] метод, отвечающий таким требованиям, основан на двухфазной процедуре, которая реализует преобразование вейвлет-отображения речевого сигнала Н-эквивалентными матрицами.

Анализ время-частотных и вейвлет-пре-образований нестационарных сигналов в информационно-измерительных системах (ИИС) показал, что обработка в вейвлет-области является эффективным методом идентификации свойств сигнала и адаптивной фильтрации с подстройкой порога дискриминации в соответствии с изменением характеристик сопутствующего шума. Метод вейвлет-преобразования применен при разработке алгоритма идентификации типа интервала речь / пауза (шум) и вейвлет-фильтрации речевого сигнала [6, 7, 8].

Здесь мы решаем задачу применения вейвлет-преобразования для скрытной передачи речевой информации.

ОБЩИЕ ХАРАКТЕРИСТИКИ ПРИМЕНЕНИЯ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ ЦЕЛЕЙ

СКРЕМБЛИРОВАНИЯ

Применение вейвлет-преобразования в алгоритме скремблирования позволяет использовать такие его важные свойства, как наличие быстрых алгоритмов преобразования и полное восстановление сигнала, включая фазовые соотношения частотных компонент.

Использование Н-эквивалентных матриц позволяет добиться высокой безопасности скремблированного сигнала, поскольку эта фаза преобразования на вейвлет-отображении сигнала реализует превращение каждой компоненты вектора вейвлет-коэффициентов в функцию от всех остальных компонент. Таким образом, вейвлет-образ полностью меняет свою структуру и, следовательно, структуру время-частотного портрета речевого сигнала. Это изменение происходит так, как если бы каждый элемент живописного полотна заменили взвешенной суммой всех остальных его элементов. При этом мощность множества Н-экви-валентных матриц настолько велика, что по количеству ключей метод существенно превосходит традиционные методы скремблирования.

Вейвлет-преобразованием (ВП) преодолевается недостаток частотных скремблеров, имеющих равномерное разбиение частотной полосы сигнала на субполосы. ВП имеет диадное разбиение частотной полосы и постоянное относительное разрешение во всем диапазоне частот сигнала. Это позволяет уменьшить ширину субполос в низкочастотной области и получить более равномерное распределение энергии сигнала по субполосам.

Для выполнения вейвлет-преобразования скремблер включает 4 каскада блоков квадратурно-зеркальных фильтров, на выходе которых получаются двоично-децимированные коэффициенты вейвлет-преобразования речевого сигнала. Использование коротких вейвлет-фильтров позволяет выполнять преобразование в реальном времени. Коэффициенты фильтра определяются видом используемого вейвлет-базиса. Выбор вида базиса и порядок его изменения (синхронизировано с приемником) является дополнительной степенью свободы при формировании ключа скремблирования.

Блок квадратурно-зеркальных фильтров состоит из низкочастотного фильтра { h i } i= 1, 2 … , выход которого дает аппроксимацию сигнала на текущем масштабе, и полосового фильтра { g i } i= 1, 2 … , выход которого дает детали как разницу аппроксимации на двух соседних уровнях масштаба.

Коэффициенты импульсной характеристики фильтра низкой частоты {hi}i=1, 2,… соответствуют уравнению связи между масштабирующими функциями на двух соседних уровнях разложения [9]

ф (1 ) = \2 - £ h n . ф (2 1 - n ).            (3)

n

Коэффициенты импульсной характеристики фильтра высокой частоты { g i } i= ₁, ₂,... соответствуют уравнению связи между масштабирующей и вейв-лет-функциями на двух соседних уровнях разложения

¥ ^{( 1} ) = V2 - ^ g n ф (2 t - n ),         ⁽⁴⁾

n где ф(1), у(1) — масштабирующая и вейвлет-функция на текущем уровне разложения; ф(21 - n), i/(21 - n) — масштабирующая и вейвлет-функция на предыдущем уровне разложения.

Коэффициенты фильтров {gi} i=1, 2,... и {hi} i=1, 2,... связаны соотношением gn = (- 1)n - h-n+21+1. (5)

Для базисных функций вейвлет-преобразования с компактной областью определения фильтры { h i } i= ₁, ₂,... и { g i } i= ₁,₂,... систематизированы в [10] и доступны в программных средствах.

Блок анализа, реализуемый каскадом квадратурно-зеркальных фильтров (КЗФ), осуществляет преобразование коэффициентов аппроксимации масштаба (j- 1)-уровня к j-му уровню согласно соотношению где dJk — коэффициент деталей, дающий отличие аппроксимации на соседних уровнях масштаба. Аппроксимацией на нулевом уровне масштаба являются отсчеты сигнала.

Таким образом, в результате вейвлет-пре-образования получается экономное представление сигнала на J уровнях разложения. Коэффициенты вейвлет-разложения подвергаются скремблированию с использованием Н-эквивалентных матриц S , которые получаются путем перестановок строк и столбцов в матрицах Адамара

^S = N TT P - H - P 2 . (⁸)

где Р ₁ — матрица перестановки строк, Р ₂ — матрица перестановки столбцов, N — порядок матрицы Адамара H .

ОПИСАНИЕ ПРОЦЕДУРЫ СКРЕМБЛИРОВАНИЯ

Процедура скремблирования включает получение матрицы Адамара H требуемой размерности; генерацию матриц P 1 и P 2 ; умножение некоторых строк и некоторых столбцов на -1; получение H-эквивалентной матрицы для скремблирования фрейма сигнала.

Матрицы Адамара H _N (порядок N = 2, N = 4 n или N = 2 ⁿ ) при дополнительной нормировке

1 _H

N ^1/2 N

удовлетворяют свойству ортогонально- ck = 2 hn-2к - cf1,

сти

H ^{- 1} = (1/ N ) - H T .

где c _k ^j — коэффициенты аппроксимации сигнала на j -ом уровне.

Этот же блок КЗФ на основе полосового фильтра М=1.2.

{ g i } i= ₁,₂, ... определяет коэффициенты разложения разности аппроксимаций

Получение матриц Адамара порядка более 4 реализуется с помощью алгоритма Сильвестера [11], согласно которому Н-матрица размерности N ₁ х N ₂ может быть получена как кронекерово произведение матриц размерностей N ₁ и N ₂:

на уровнях j -1 и j согласно соотношению

H N 1 Х N ₂ = H n 1 ® H n _г ,              (10)

d k = ^ g n - 2 к - <^Х,             (7)

n где ® — символ кронекерова произведения матриц, которое выражается правилом

	I" N 1	11	H N 2	[ h N 1	1 12	H N 2   •	• [h n 1	] 1 N 1	H N 2
H N 1 ® H N 2 =	[ И N 1	1 ,1	H N 2	[ H n 1	] 22	H N 2   •	• [h n 1	2 N 1	- H N 2
	_ [ Н N 1	N 1 1	- H N 2	[ И n 1	N 1 2	- H N 2   •	• [h n 1	N 1 N 1	- H N

где [ h N 1 ] , — элемент матрицы H N 1 , стоящий на пересечении i -го столбца и j -й строки; N ₁ — размерность матрицы H n 1 ; [ H N 1 ] , _y • H _N 2 — результат умножения матрицы H _{N 2} на элемент [ H n ₁ 1 , матрицы.

Таким образом, используя кронекерово произведение, из H-матрицы второго порядка Н 2 можно построить другую Н-матрицу любого порядка 2 ⁿ . Для получения матриц Адамара с размерностями типа N=pⁿ+ 1, где р — простое число, можно использовать схему Палея [12].

выполняется путем преобразования вектора u с помощью H-эквивалентной матрицы S . Вектор v скремблированных коэффициентов на сегменте сигнала определяется соотношением

v = S • u .                        (14)

Способ скремблирования без конкатенации строк

СКРЕМБЛИРОВАНИЕ ВЕЙВЛЕТ-КОЭФФИЦИЕНТОВ

Способ предполагает использование нескольких матриц Адамара для скремблирования сегмента сигнала. Число матриц соответствует количеству наборов вейвлет-коэффициентов. При четырехуровневом вейвлет-разложении для скремблиро-

Скремблирование выполняется на временнóм сегменте сигнала. Величина сегмента определяет задержку скремблирования, которая должна быть в пределах 10–100 мс. Слишком малая величина сегмента не обеспечивает достаточной безопасно-

вания пяти ^{{ d}k ^} k = 1,...,64 , предложено

наборов коэффициентов { d k } _k = 1 ₁₂₈,

^{{ d}k ^} k = 1,...,32 ’

I k = 1,...,16 ’       c k J k = 1,...,16

использовать пять матриц Адамара

соответствующей размерности:      H ₁ ( _{128 x 128} ) ,

сти скремблирования. При частоте дискретизации 22.05 кГц сегмент может быть выбран в 256 от-

счетов при длине сегмента 11.6 мс.

На сегменте выполняется   вейвлет-пре-

^H 2(64 X 64) , ^H 3(32 X 32) , ^H 4(16 x 16) , ^H 5(16 x 16) ^.

Скремблирование выполняется путем преобразования векторов коэффициентов вейвлет-разложения

образование, результатом которого является со-

вокупность наборов коэффициентов

^{ d k I k = 1,...,64

^{ d k I k = 1,...,32

I d k I k = 1,...,16

^{ d k ^} k = 1,...,128 ^,

^{ c k I k = 1,...,16 .

Общее количество коэффициентов равно числу отсчетов на сегменте. Над этими коэффициентами выполняется преобразование с использованием матриц Адамара. Можно использовать два варианта скремблирования вейвлет-коэффициентов: с конкатенацией или без конкатенации строк, содержащих вейвлет-коэффициенты в разных про-

11 1 22

^U 1 = ^{[ d} 1 , d 2 , • ■, d 128 ^] , u 2 = ^{[ d} 1 , d 2 u 3 = ^{[ d} 13 , d I , — , d 332 ^] , u 4 = ^{[ d} 14 , d 24 u 5 = t 14 , с 4 , — , с 146 ^]

■, d 624 ^] ,

■, d 146 ] ,

странствах разложения.

Способ скремблирования с конкатенацией строк

Способ предполагает объединение вейвлет-коэффициентов во всех пространствах разложения

{uk }k=1,...,256   {dk }k=1,...,128 U {dk }k=1,...,64 I и {dk 1=132 U {dk Ik=,16 U {c^L 16

∪

и представление в виде единого вектора u = [d1, d 2, — , d^, d 12, d 2 , ••■,

2  33

64 ^, 1 ^, 2

, d 3 ³ 2 , … , d 1 ⁴, d 2 ⁴, … ,

4    44    4

d ₁₆, … , c ₁, c ₂, … , c ₁₆ .

При способе с конкатенацией скремблирование

с помощью набора H-эквивалентных матриц S

v _; = S_r u _; z = 1, — ,5, (15) где v — векторы скремблированных коэффициентов на сегменте сигнала; S_; = — P_h • H • P_2; —

N набор H-эквивалентных матриц соответствующей размерности.

Таким образом, вариант с конкатенацией вейв-лет-коэффициентов позволяет выполнять скремблирование путем линейной комбинации коэффициентов на всех пространствах разложения, соответствующих разным частотным полосам сигнала. Поэтому метод может быть условно отнесен к время-частотным методам скремблирования, которые обеспечивают более высокую безопасность, но требуют большего объема вычислений, поскольку используют матрицы Адамара высокой размерности.

Метод без конкатенации вейвлет-коэф-фициентов предполагает выполнение линейной комбинации коэффициентов отдельно в каждом пространстве разложения и поэтому может быть

условно отнесен к методам временнóго скремблирования, которые обладают меньшей безопасностью и выполняют меньше вычислений, используя матрицы Адамара меньшей размерности.

ДЕСКРЕМБЛИРОВАНИЕ ВЕЙВЛЕТ-КОЭФФИЦИЕНТОВ

Дескремблирование включает преобразование вейвлет-коэффициентов с помощью обратных H-эквивалентных матриц S ^–1 и последующее восстановление сигнала обратным вейвлет-пре-образованием, с использованием сопряженных квадратурных фильтров h* и g* . Дескремблиро-ванный сигнал определяется преобразованием

из пространств разложения:

{ d. } . = 1,...,128 = { u . } к = 1,•••,128 ’
{dk } . = 1,,,,,64 = { u . } . = 129,...,192 ’
{ d k } . = 1,...,32 = { “ . } . = 193,,224 ’	(19)
{ d . } . = 1,,,,,16 = { Uk } . = 225,•••,240 ’
{ c . } . = 1,,,,,16 = { u . } . = 241,•••,256 •

В варианте без конкатенации вейвлет-коэф-фициентов они могут быть получены непосредственно из соотношения

« , = S • v T ,                     (20)

s = W - 1 • S ^{- 1} • v T ,

где s — дескремблированный сигнал; W ¹ — об

где также при отсутствии ошибок скремблирования и дескремблирования u , = u ,■ ,

ратное      вейвлет-преобразование;       S ¹ =

_N 1/2

( P i • H • P 2 ) ^{- 1}

— обратная H-эквивалентная

матрица. Преимуществом матриц Адамара является то, что процесс дескремблирования выполняется за счет процедуры получения S ^{- 1} простым транспонированием нормированной ортогональной матрицы

S - 1 = i ( P 1 • H • P 2 ) ^{- 1} = i ( P 1 • H • P 2 ) ^Т • (17) _N 1/2                 _N 1/2

Таким образом, использование в процессе скремблирования и дескремблирования нормированной ортогональной матрицы позволяет заменить сложную операцию обращения матрицы на операцию ее транспонирования, которая выполняется достаточно быстро и не вносит дополнительных задержек.

При выполнении дескремблирования сигнала для варианта с конкатенацией вейвлет-коэф-фициентов получается вектор, содержащий упорядоченные вейвлет-коэффициенты

u = [ d 11 , d 2 , — , d ^, d 1 ², d 22,.

2  33     3     4

d 64 , d 1 , d 2 , — , d 32 , — , d 1 , d,

4    44    4

d 16 , ^— , ^c1 , c 2 , ^— , c 16 J ,

,

,

2 , ^— ,

и при отсутствии ошибок скремблирования и дескремблирования имеется полное восстановление речевого сигнала: u = u .

Из вектора u могут быть выделены отдельные группы вейвлет-коэффициентов для каждого

11   1       22

^u 1 = \ d 1 , d 2 , • — d 128 ^] , u 2 = \d 1 , dг

^u 3 = \ ^d 1 , d 2 ^{, —} , d 32 ^] ,

u 5 = \ c 14 , c 24 , — , c 146 ] •

u 4 = \ d 1⁴, d 2

■, ^d 64 ^] ,

■, d 146 ] , (21)

Восстановление сигнала из дескремблирован-ных вейвлет-коэффициентов выполняется с помо-

щью схемы синтеза, которая заключается в полу-

чении c – 1 из c и d [10]. Для этого используется набор квадратурно-зеркальных фильтров h n и g n .

Входом этих фильтров служат коэффициенты

c . } . =u

и { d / } . .12..

при j = 1, 2, …, J . Восста-

новление все более точной аппроксимации выполняется с помощью сопряженных фильтров соглас-

но соотношению

c^{j -1} = X c^{j /j} d^j (HA cm / . hm - 2 . • c. + gm - 2 к • d. • ⁽22)

k

Таким образом, скремблер, основанный на вейвлет-преобразовании, не вносит дополнительных искажений в сигнал, поскольку использует свойство полного восстановления, характерное для вейвлет-преобразования. При выборе биорто-гонального вейвлет-базиса фильтры разложения и восстановления имеют линейную фазовую характеристику и не вносят дополнительных фазовых искажений. Для биортогонального базиса фильтры разложения и восстановления могут иметь разную длину, и это позволяет балансировать объем вычислений при скремблировании и дескремблировании.

Распределенная система обработки речевой информации может использовать аналоговые и цифровые каналы связи. Сигнал, содержащий

конфиденциальную информацию, может передаваться по аналоговому каналу, соединяющему компьютеры через модем, или по цифровому каналу в локальной или глобальной компьютерной сети.

АЛГОРИТМЫ ЗАЩИТЫ СИГНАЛА

В АНАЛОГОВОМ И ЦИФРОВОМ КАНАЛАХ СВЯЗИ

Защита сигнала в аналоговом канале может быть обеспечена разработанным методом скремблирования с дополнительными преобразованиями сигнала в цифровую и аналоговую формы (рис. 1, а). Алгоритм включает вейвлет-преобразование сегмента речевого сигнала, преобразование коэффициентов с помощью Н-эквивалентной матрицы и обратное ВП, которое позволяет получить скремблированный сигнал в аналоговой форме.

Защита сигнала, передаваемого по цифровому каналу, осуществляется применением алгоритма, представленного на рис. 1, б. После Н-экви-валентного преобразования вейвлет-коэффици-ентов производится формирование пакетов данных для передачи по цифровому каналу. На стороне декодера выполняется дескремблирование с помощью транспонированных Н-эквивалентных матриц и обратное ВП, которое позволяет восстановить исходный сигнал в цифровой форме.

КОЛИЧЕСТВО КЛЮЧЕЙ

При выполнении алгоритма скремблирования задается базовый ключ и ключ сеанса. Ключ сеанса обеспечивает генерацию Н-эквивалентной матрицы и изменяется на каждом сегменте сигнала. Базовый ключ изменяется редко и задает последовательность ключей сеанса. Большее количество

а

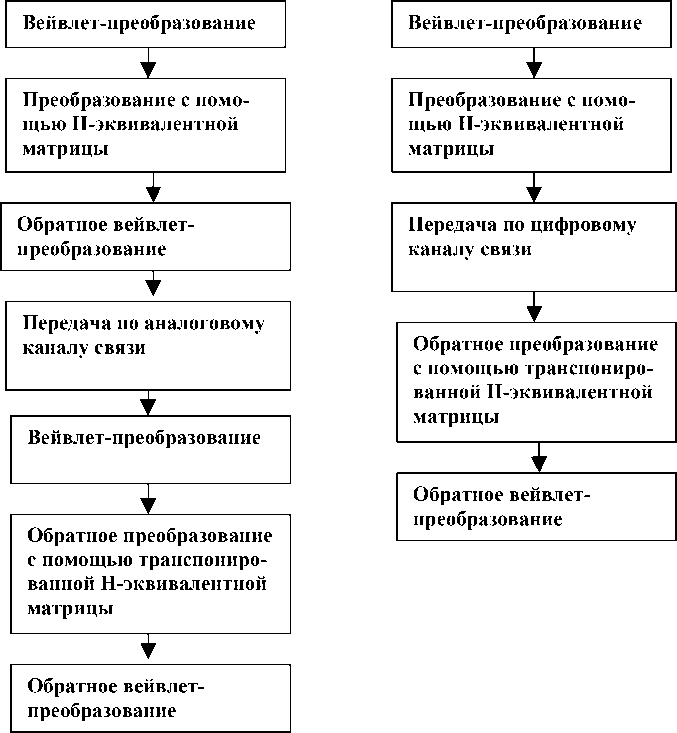
Рис. 1. Варианты алгоритма скремблирования в аналоговом (а) и цифровом (б) каналах связи

б

ключей сеанса дает высокую защищенность системы и позволяет реже изменять базовый ключ, поэтому количество ключей сеанса является важной характеристикой алгоритма скремблирования.

Для алгоритма скремблирования с конкатенацией вейвлет-коэффициентов число ключей сеанса определяется количеством H-эквивалентных матриц, размерность которых зависит от длины конкатенированного вектора вейвлет-коэффициентов

K = ( 2 N • N ! ) ², (23)

где N — размерность H-эквивалентной матрицы, равная длине сегмента сигнала; K — количество ключей. Зависимость логарифма количества ключей от длины сегмента сигнала приведена в табл. 1. Для алгоритма без конкатенации количество ключей определяется количеством H-эквивалентных матриц в каждом пространстве вейв-лет-разложения

Табл. 1. Зависимость количества ключей от длины сегмента сигнала для формы алгоритма скремблирования с конкатенацией вейвлет-коэффициентов

N	lg( K )	N	lg( K )
64	108	256	584
128	254	512	1381

Табл. 2. Зависимость количества ключей от длины сегмента сигнала для формы алгоритма скремблирования без конкатенации вейвлет-коэффициентов

N Число пространств lg(K) 4 44 128 5 32 6 25 7 21 4 108 256 5 81 6 63 7 52 4 254 512 5 192 6 153 7 127 f N

K = 2 M •

m

/

V

где M — число подпространств вейвлет-разло-жения; N — длина сегмента; K — количество ключей. Зависимость количества ключей от длины сегмента сигнала приведена в табл. 2. Некоторые H-эквивалентные матрицы, которые производятся в соответствии с алгоритмом Сельвестера, повторяются, поэтому реальное число ключей несколько меньше, чем число ключей, указанное в табл. 1 и 2.

Анализ показывает, что предложенный метод скремблирования имеет количество ключей, превышающее число ключей в методах частотного, временнóго и время-частотного скремблирования.

СПЕКТР СКРЕМБЛИРОВАННОГО СИГНАЛА

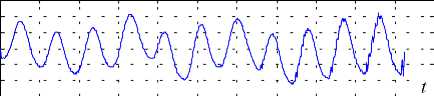
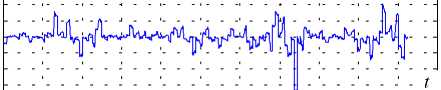
Описанный алгоритм реализован в среде Matlab 5.3 и выполнено скремблирование с конкатенацией и без конкатенации вейвлет-коэф-фициентов в пространствах разложения речевого сигнала. Наиболее сложен для скремблирования сигнал, представляющий собой гласные фонемы [13], который плохо скрывается существующими методами частотного, временнóго и время-частотного скремблирования. Поэтому для проверки предложенного метода скремблирования использованы сегменты, содержащие гласные фонемы. На рис. 2 приведены графики, которые представляют сегмент исходного сигнала фонемы (i:) и его скремблированную форму. В результате скремблирования формантная частота фонемы скрыта и не видна на графике. Двухмерная форма (в пространстве разложения сигнала время—индекс)

а

0    100   200   300   400   500   600   700   800   900  1000  1100

0.4

0.2

-0.2

-0.4

-0.6

0    100   200   300   400   500   600   700   800   900  1000  1100

б

Рис. 2. Исходный (а) и скремблированный (б) сигналы

б

-1 0

H~ (s) = NP (J H (s/ ~.)= j=1

= N P ( ~ ) • 1-2 P ( sM ' ) • log [ P ( s i /' ) 1 | = j = 1             I i                                        J

= -2 2 P ( s i ,~ _y ) ’ log [ P ( s i /S y ) ] ,              (26)

i = 1 j = 1

-2 0

-30

-40

уА^у лт^гЛУу- ■ ■

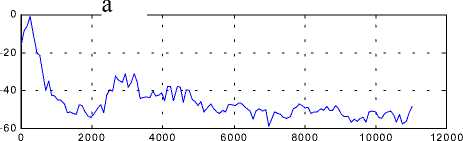
Рис. 3. Спектры мощности исходного (а) и скремблированного (б)сигналов

вейвлет-представлений исходного и скремблированного сигналов демонстрирует более равномерное распределение вейвлет-коэффициентов по уровням разложения в скремблированном сигнале. Сравнение (рис. 3) спектров мощности исходного и скремблированного сигналов также показывает, что скремблированный сигнал имеет почти равномерное распределение мощности по частотному диапазону.

Аналогичные результаты получены для других фонем. Таким образом, можно заключить, что в результате скремблирования вейвлет-коэф-фициентов с использованием матриц Адамара узкополосный сигнал приобретает спектр мощности, близкий к равномерному спектру.

где P ( s i ) — распределение вероятностей скремблированного сигнала; P ( s i / s jj ) — условное распределение вероятностей сигнала s_i при известном скремблированном значении ~ ; P ( s i ,') — совместное распределение вероятностей исходного и скремблированного сигналов; H ( s i / ' ) — условная энтропия сигнала s_i при известном скремблированном значении ' .

Оценка остаточной информации в скремблированном сигнале I ( s , ~) может быть выражена и на основе соотношения (27), отражающего взаимосвязь совместной, условной и частной энтропий:

H ( s |~ ) = H ( s ,~ ) - H (~ ).         (27)

Преобразование (27) приводит к удобной форме для информации:

I ( s ,~ ) = H ( s ) - H ( s |~ ) =

= H ( s ) - H ( s ,~ ) + H (~ ),               (28)

I ( s ,~) = 22 [ - p ( s ,~)log p ( s ) +

+ p ( s , ~) log p ( s , ~) - p ( s , ~) log p (~ ) ] =

ОСТАТОЧНАЯ ИНФОРМАТИВНОСТЬ СКРЕМБЛИРОВАННОГО СИГНАЛА

Мера качества алгоритма скремблирования — это количество информации I ( 5 ,~ ) об исходном сигнале s , которое содержится в скремблированной форме сигнала ^~ s . С использованием меры Шеннона остаточное количество информации определяется разностью энтропии H ( s ) исходного сигнала и условной энтропии H ~ _s ( s ) сигнала по его скремблированной форме [14],[15]

I ( s ,~) = H ( s ) - H ~ ( s ). (25)

Энтропия H ~ ( s ) — средняя энтропия (условная по распределению скремблированного сигнала) определяется выражением

= 22

p ( s ,~)log

p ^{( s ,S}) p ( s ) p (~ )

В качестве первого приближения использована нормальная аппроксимация для плотностей распределения сигнала, скремблированного сигнала, совместной и условной плотности сигнала и скремблированного сигнала:

P ( s ) = —j= --exp

Т2 Л - o s

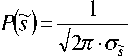
- exp

7   2 A

s

V

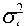
Г —2 A s

o '

s ⁷

^{P ( s} , ^s )=------ ¹ /—_? ^x

2 no _s o~-xl 1 - r

x exp

2        ,'-'2

1 s s 2 r - s - s 2 ( 1 - 7^) ( T? ⁺ O F "  A OsT T

P (s/ ~ ) =

P (s,~ ) P (~)

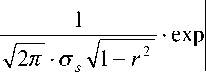
/ s^ ₊ ~ 2 ^- ( 2 r ² - 1 1 - Ir-s - l

2(1 - r 2 ) ^ °2        О~         OsO~ где os и о~ — среднеквадратические отклонения сигнала s и скремблированного сигнала s ; r — коэффициент корреляции между ними.

В этом случае выражение для количества информации о сигнале в его скремблированной форме приобретает вид

NN

I (s ,s Md i=lj=l

2 по о ~ V1 - r²

- exp

1        s²   j - ² r ^{- s}i^sj

2 ( 1 - r ² ) ^ G^    о ~     ° _s ° ~

X log

V^{1 -} r ^{2 -} exp [ ^{- (} s² /° ² + ~² ° ~ ^{) ]}

- exp

В такой же последовательности получена остаточная информация для экспоненциальностепенного распределения, которое более полно описывает статистику речевых сигналов [8]. Для плотности сигнала использовано выражение

p ⁽ s ) =

a

2 Хо Г(1/ a )

exp -

I

s

а Л

Ло

У

а для совместной плотности сигнала и его скремблированной формы (с учетом возможной корреляции) — выражение

p ^{( s , s} ) =

a ² V1 - r²

X

4( Ло Х Л ~ о ~ )[Г(1/ a )]²

1       _- s² , ^sj • - ^{2 r - s}i^sj

2 ( 1 - r ² ) о² о ~ о о _?

^ ^{s s s s}

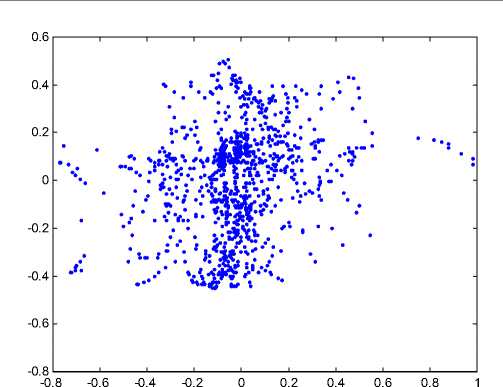
Рис. 4. Корреляционное поле исходного сигнала и скремблированного сигнала

(

^X exp

I

a s2        2 rs ~~

—;—V + "У----;--1Г

Л 2 о²  ЛоЛо ~   ( Л ~ о ~ )²

s s s ss s

У

Количество остаточной информации I(s,~s) , которое для обеспечения безопасности должно быть как можно меньше, зависит от коэффициента корреляции r между исходным и скремблированным сигналами. Для сегментов гласных фонем (фрагментов речевого сигнала, наиболее трудных для закрытия информации) получены оценки коэффициентов корреляции. Корреляционное поле для сегмента сигнала показывает, что корреляция практически отсутствует (рис. 4).

Оценки коэффициентов корреляции между ис- ходным и скремблированным сигналами, полученные для разных гласных фонем, находятся в диапазоне –0.24 … 0.3 со средним значением коэффициента корреляции 0.06 (табл. 3).

Теоретическая статистика указывает на довольно широкие доверительные пределы коэффициента корреляции. Например, при N = 400 и доверительной вероятности 0.99 экспериментальной оценке коэффициента 0.1 может соответствовать интервал (–0.03 … +0.2). В связи с этим

Табл. 3. Значения коэффициентов корреляции r между скремблированным и исходным сигналами

Фонема r [i] –0.10 0.30 [o] –0.24 0.08 [a] 0.07 0.08 [u] 0.027 0.17 [e] –0.05 0.27 для остаточной информации скремблированной формы относительно основного сигнала рассчитан критерий взаимной информации для коэффициента корреляции до 0.25. Использовано как нормальное приближение, так и экспоненциальностепенной закон для распределения двух форм сигнала. Результаты показывают, что относительная остаточная информация при нормальной аппроксимации не превышает 0.8 %, а для экспоненциально-степенного распределения с различным значением параметра формы [8] имеет верхнюю границу 0.6 – 1 %.

Таким образом, корреляционный анализ показывает, что между исходным и скремблированным сигналами практически отсутствует корреляция, и это обеспечивает малую остаточную информативность скремблированного сигнала. Информационный критерий подтверждает высокую защищенность речевого сигнала при предложенном методе скремблирования на основе вейвлет-преобразования и матриц Адамара.

ЗАКЛЮЧЕНИЕ

Предложен и исследован метод скрытой передачи информационного сигнала речи для распределенной системы, включающей локально-сетевую структуру ЭВМ. Метод использует скремблирование на основе модифицированного вейвлет-преобразования. Алгоритм скремблирования включает преобразование матрицами Адамара вейвлет-отображения сигнала, имеет две разновидности (с конкатенацией и без конкатенации вейвлет-коэффициентов сигнала) и предлагается в двух формах: для аналоговых и цифровых каналов.

Введение двухфазного преобразования обеспечивает методу высокие показатели качества информационной безопасности по количеству ключей и минимальной величине остаточной информации в скремблированном сигнале. Для получения этих показателей применены методы теории матриц Адамара, комбинаторного, корреляционного анализа (для наиболее трудно скремблируемых элементов — фонем) и теоретикоинформационный метод. Выполненные количественные оценки показывают преимущество метода двухфазного скремблирования над традиционными его формами.