Слепая идентифицируемость линейной динамической модели канала связи

В задачах, относящихся к обработке сигналов в системах связи, часто возникает проблема построения математических моделей каналов передачи непосредственно по регистрируемым данным, в условиях, когда тестирование канала испытательным импульсом невозможно или нежелательно [1; 2]. В этих случаях говорят о задаче слепой идентификации канала связи.

В большинстве практических случаев в телекоммуникациях речь идет о линейной, нестационарной модели взаимодействия входных, выходных сигналов и помех, т.е. о модели линейной динамической системы (ЛДС) [3; 4].

Задача идентификации линейной динамической системы в общем случае тесно связана с задачами управляемости и наблюдаемости. В теории автоматического управления проблема нахождения условий управляемости (возможности приведения динамической системы в заданное состояние с помощью управляющих воздействий за конечное время) и наблюдаемости (возможности определения переменных состояния по измерениям физических переменных в системе) была корректно поставлена лишь во второй половине 20-го века.

Решение проблем управляемости и наблюдаемости было найдено Р. Калманом в рамках моделей «вход-состояние-выход». В рамках данной модели предполагается, что система описывается вектором состояний, часть которых может быть недоступна для управления или наблюдения. При этом выбор вектора состояний системы не является единственным, и для него не существует общих принципов выбора [3; 4].

В задачах идентификации систем на первое место выходит понятие идентифицируемости системы. В существующей литературе имеется большое многообразие подходов к определению этого свойства систем, зависящих, к тому же, от особенностей построения процесса идентификации [4; 6; 7].

В данной работе мы рассмотрим связь понятий идентифицируемости, наблюдаемости и управляемости ЛДС, используемых для описания систем, опираясь в основном на работу [6].

Далее мы рассмотрим задачу слепой идентифицируемости ЛДС и сформулируем условия, при которых задача имеет решение.

Слепая идентификация одномерного канала связи (SISO) часто рассматривается как возможность повышения скорости в системах передачи данных, за счет отказа от периодического тестирования канала. Однако большинство найденных способов слепой оценки параметров канала имеют низкую помехоустойчивость, что ограничивает возможность практического применения данных методов. Между тем, в системах, использующих канал с несколькими входами и выходами (MIMO) или с одним входом и несколькими выходами (SIMO) ситуация с помехоустойчивостью более оптимистичная.

Задача слепой идентификации систем связи имеет большую библиографию, с которой можно ознакомиться, например в [8]. Теоремы слепой идентификации SIMO канала можно найти в [9], для MIMO канала в [10], для SISO канала [11].

В указанной литературе рассматривается математические модели систем «вход-выход», возможность использования моделей «вход-состоя-ние-выход» остается за рамками рассмотрения. Данная статья частично восполняет этот пробел.

Управляемость и наблюдаемость динамических систем

Как известно линейная динамическая система произвольного вида, задается в дискретном времени матрицами A , B , C , D .

' u [ k + 1] = Au [ k ] + Bx [ к ],

< у [ к ] = Cu [ к ] + Dn [ к ],              (1)

_ u [0] = 0.

где х [ к ] - [ G j ], входной вектор, у [ к ] - выходной вектор, u [ k ] – вектор состояний системы, A , B , Ñ , D – постоянные матрицы.

ЛДС называется управляемой, если в отсутствии шумов для любых двух состояний u [ 0 ] и u [ n ] , существует управляющее входное воздействие, при котором ЛДС может быть переведена из начального состояния в конечное.

Теорема 1. Критерий управляемости (P. Кал-ман). Динамическая система управляема тогда и только тогда, когда матрица управляемости

имеет ранг равный n.

Запишем соответствующие состояния системы: u [1] = Au [0] + Bx [0],

u [2] = Au [1] =

= A ² 2 u [0] + ABx [0] + Bx [1],

u [ n ] = Au [ n - 1] =

= A ⁿ u [0] + A ⁿ Bx [0] + ... + Bx [ n - 1].

Так как u [ 0 ] и A - известны заранее, то для неизвестного управляющего воздействия можно записать систему уравнений в виде

u[n] - Anu[0] = AnBx[0] +... + Bx[n -1] = г x[ n-1]

= ( B AB

A ^{n - 1} B )

x [ n - 2]

( x [0] )

Если условие теоремы 1 выполняется, то решение данного уравнения относительно управляющего воздействия существует для каждого из m входов системы x [ k ].

Под наблюдаемой системой в дискретном времени будем понимать однородную систему, состояние которой u [0] можно в отсутствии шумов однозначно восстановить по выходным сигналам y [0] , y [1] ,…, y [ n ] .

Запишем связь выходных сигналов однородной системы и ее состояний

у [0] = Cu o

y [1] = CAu [0],

у [2] = CAu [1] = CA ² u [0],

у [ n ] = CAu [ n - 1] = CA ^{n - 1} u [0].

В матричной форме можно записать

Г у [0] ^ у [1] у [2]	=	Cu 0 CAu [0] CA 2 u [0]	=	Г C    ^ CA CA 2	u [0]
... ( у [ n ] ;		... CA n - 1 u [0] ;		... . CA n - 1 )

Условием наблюдаемости является требование rank ( C t C t A t C t (A ² ) t.„Ct ( A ^{n - 1}) t ) = n , что соответствует следующей теореме.

Теорема 2. Критерий полной наблюдаемости (P Калман). Для того чтобы система (1) была полностью наблюдаемой необходимо и достаточно, чтобы матрица наблюдаемости

W C = ( C t C t A t C t (A ² ) t. „ C t ( A ^{n - 1}) t ) , размерности n x np , имела ранг равный n .

Идентифицируемость линейной динамической системы

В задачах идентификации оптических систем на первое место выходит понятие идентифицируемости системы. Рассмотрим некоторые имеющиеся подходы к пониманию данной проблемы в форме последовательно доказываемых утверждений.

Допустим, имеется однородная ЛДС, описываемая следующим уравнениями в пространстве состояний в дискретном времени

u [ к + 1] = Au [ к ],

< у [ к ] = Eu [ к ], . (2) u [0] = u o .

Под идентифицируемостью системы в данном случае будем понимать возможность однозначного определения матрицы A и ненулевого вектора начальных условий u ₀ по набору у [ к ] в условиях отсутствия помех.

Теорема 3. ЛДС вида (2) идентифицируема тогда и только тогда, когда n x n матрица

Wo = (u0 Au0 ... A(n-1)u0 ) , имеет полный ранг.

Доказательство.

Пусть для идентификации доступны данные:

u [0] = U o

u [1] = Au [0],

u [2] = Au [1] = A ² u [0],

...

u [ n ] = Au [ n - 1] = A ^{n - 1} u [0].

Вектор начальных условий u ₀ определяется тривиальным образом из первого уравнения, оставшиеся неизвестные элементы матрицы A определяются с помощью следующей системы уравнений.

( u [1] u [2] ... u [ n ] ) = W 0 A‘ .

Для существования единственного решения необходимо и достаточно, чтобы rank ( W ₀ ) = n . Теорема доказана.

Допустим, имеется неоднородная ЛДС, описываемая следующим уравнениями в пространстве состояний в дискретном времени

u [ к + 1] = Au [ k ] + Bx [ к ],

< у [ к ] = Eu [ к ],               .          (3)

u [0] = U 0 .

Под идентифицируемостью системы в данном случае будем понимать возможность однозначного определения матриц A , B и ненулевого вектора начальных условий u ₀ по набору у [ к ] при управляемом входе, в условиях отсутствия помех. Другими словами, нам доступна возможность сформировать входные сигналы таким образом, чтобы была возможна идентификация системы. Воспользуемся этим и сформулируем следующую теорему.

Теорема 4. ЛДС вида (3) идентифицируема тогда и только тогда, когда гаик ( W ₀ ) = n , а входные управляющие сигналы могут быть нулевыми и образовывать множество линейно независимых векторов вида { Bx [ к + 1], Bx [ к + 2],..., Bx [ к + m ] } .

Доказательство.

Допустим, для идентификации доступны данные:

u [0] = U 0

u [1] = Au [0] + Bx [0],

u [2] = Au [1] + Bx [1] =            ⁽⁴⁾

= A ² u [0] + ABx [0] + Bx [1],

u [ n + m ] = Au [ n + m - 1 ] + Bx [ n + m - 1 ] =

= A ^{n + m} u [0] + A ^{n + m} Bx [0] + ... + Bx [ n + m - 1].

Вектор начальных условий u ₀ определяется тривиальным образом из первого уравнения, оставшиеся неизвестные элементы матриц A и B определяются с помощью следующей системы ( n + m ) n линейных уравнений

( u [1] u [2] ... u [ n + m ] ) =

' u * [0]          x t [0]

= u * [1]         x t [1]

v u t [ n + m -1] x t [ n + m -1] y f A ■

I ^B '

Представим матрицу системы уравнений (5) в виде блочной матрицы

Q =

f U 1

I U 2

X 1 )

X 2 J ,

где U 1 и X ₂ - квадратные матрицы размером n x n и m x m соответственно, при этом

	f u t [0]	^	f     u t [ n ]
U 1 =	u t [1]	, U 2 =	u t [ n + 1]
	v u t [ n - 1]	/	v u t [ n + m - 1] y
	' x t [0] "		t x [ n ]
X , =	x t [1]	, X 2 =	x [ n + 1]
	. x t [ n - 1] ,		v x t [ n + m - 1] y

В соответствии с определением идентифицируемости, положим, что в процессе идентификации первые n входных отсчетов нулевые, а оставшиеся таковы, что det ( X ₂ ) # 0. Тогда для идентифицируемости системы необходимо и достаточно, чтобы rank ( U 1 ) = n , rank ( X ₂ ) = m . Таким образом rank ( Q ) = n + m .

Легко проверить, что при таком входном сигнале U 1 = W ₀, а из условия rank ( X 1 ) = m следует, что вектора { Bx [ n ], Bx [ n + 1],..., Bx [ n + m - 1] } – линейно независимы. Теорема доказана.

Допустим, имеется неоднородная ЛДС, описываемая следующим уравнениями в пространстве состояний в дискретном времени

u [ к + 1] = Au [ к ] + Bx [ к ],

< у [ к ] = Cu [ к ], (6) u [0] = U 0 .

Под идентифицируемостью системы в данном случае будем понимать возможность определения матриц A , B , C и, в том числе, нулевого вектора начальных условий по набору у[к] при управляемом входе, в условиях отсутствия помех.

Теорема 5. ЛДС вида (6) идентифицируема тогда и только тогда, когда:

• 1.    ЛДС полностью наблюдаема и управляема.

• 2.    rank ( W _o ) = n .

• 3.    Входные управляющие сигналы могут быть нулевыми и/или образовывать множество линейно независимых векторов.

Доказательство данной теоремы кажется вполне очевидным, если учесть имеющуюся свободу в выборе ансамбля входных сигналов, а также доказательство критерия наблюдаемости и предыдущую теорему.

Из условия наблюдаемости следует, что существует однозначное соответствие между наблюдаемыми данными и вектором состояний в любой момент времени.

Из условия управляемости следует возможность создать любые начальные условия на входе однородной модели, в том числе такие, чтобы стала возможна идентификация однородной модели системы.

Из 3-го требования теоремы следует возможность идентификации матрицы B , при известных A и C .

Доказательство.

Допустим, начальные условия ЛДС ненулевые, а входные сигналы равны нулю. Тогда на выходе однородной ЛДС наблюдаются сигналы

y [0] = C U o

y [1] = C Au [0],

...

y [ n ] = C A ⁿ u [0].

Сформируем для каждого j-го выхода вектор

У j [ ⁰ ] , такой, что

y j [ 0 ] =	' C ' CA CA 2	• u [0] = W c [ j ] u [0]
	... ч CA n - 1 ,	j

В соответствии с критерием наблюдаемости W C [ j ] имеет полный ранг и соответственно имеет обратную матрицу W ^- [ j ]. Тогда для любого j

yJ0 ] =	Г C     ^ CA CA 2	• u [0] = W c [ j ] u [0] ,
	... ч CA n - 1 v	j

	yJ1 ] =
01	0
00	1
00	0

j n-1

^- a n - 2

У j [ 0 1 =

j an

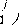
= A St УД 0]

Продолжая последовательность y j [ к ] , получим стандартную управляемую модель в пространстве состояний для j-го выхода однородной системы, у которой C S_t = ( 1 0 .. 0 ) .

Параметры A j легко восстановить из последовательности у j [ к ] , записав соответствующие линейные уравнения.

Далее, создавая на каждом i-м входе последовательность Bixi[к],Bixi[к +1],...,Bixi[к + n -1] в соответствии с 3-м условием теоремы, получим оценку

^{B i} s ^, t ^j

= W _c [ j ] B ,

' bi^ bУ bУ

Таким образом, идентифицируем строчную форму стандартной наблюдаемой модели для каждого j -го выхода и i -го входа.

УД к + 1] = A St y j [ к ] + B S :/x , [ к ],

< Z j [ к ] = C S у _у [ к ]

^[0].

Запишем передаточную функцию для каждого

-го выхода и i -го входа

„ dS ,Jz-1 + • •• + dijz"n+1 + di’jz - n wM (z) = 1 1 J -1^ n J -n+1 / J -n •

1 + a / z + ... + a n 1 z + a n z

Таким образом, если выполняются условия теоремы, то система идентифицируема, т.е. существует единственная передаточная функция MIMO системы W ( z ) , заданная матрицей дробно-рациональных функций w_{i ,} ( z ) , которую можно оценить, задавая различные сигналы на входе идентифицируемой системы.

Допустим, начальные условия ЛДС нулевые, тогда условие управляемости дает возможность задать начальные условия однородной системы, так, чтобы выполнилось требование к идентифицируемости однородной системы.

Теорема доказана.

Теперь, если это необходимо, можно построить матрицы A, C, B ЛДС. Однако, выбор ма- триц модели системы вида (4) в пространстве состояний неоднозначен, даже в случае полностью идентифицируемой системы существует много способов построения моделей данного типа, неразличимых по входу и выходу, в том числе содержащих минимальное число параметров.

Слепая идентифицируемость линейной динамической системы

Под слепой идентифицируемостью системы в данном случае будем понимать возможность определения матриц A , B , C в (6) и в том числе нулевого вектора начальных условий U q по набору y [ к ] при неизвестной входной последовательности конечной длины, в условиях отсутствия помех.

Теорема 7. SIMO ЛДС вида (6) идентифицируема вслепую тогда и только тогда, когда:

• 1.    ЛДС идентифицируема в обычном смысле.

• 2.    Передаточная матрица системы

P( z )      PM ( z ) )

IQi (z) ... Qm (z)J такова, что многочлены P. (z) Q (z) и р. (z) Qi (z) не имеют общих корней при i * j, M - число каналов.

Доказательство.

Допустим, MIMO ЛДС в дискретном времени задана в пространстве состояний системой уравнений

u [ к + 1] = Au [ к ] + Bx [ к ],

‘ y [ к ] = Cu [ к ],

_ u [0] = 0.

Применяя z-преобразование, получим z U ( z ) = AU ( z ) + BX ( z ),

Y ( z ) = CU ( z ).

Затем

U ( z ) = ( z E - A ) ^{- 1} BX ( z ), Y ( z ) = CU ( z ).

Таким образом, получим матрицу передаточных функций (передаточную матрицу) системы в виде

W ( z ) = C ( z E - A )^{- 1} B .

Если система идентифицируема в обычном смысле, то существует единственная передаточная функция MIMO системы W ( z ) , заданная матрицей дробно-рациональных функций w_{i , j} ( z ) , или в случае SIMO, вектором

^ ^P1 ^{( z} )        P M ^{( z} ) )

< Q i ( z ) ... Q m ( z ) J .

W ( z ) =

Если система полностью наблюдаема и управляема, то передаточная матрица полностью описывает систему в терминах вход-выход.

Для любого i -го и j -го выхода можно записать

Л -( ^z ) = ^{P ( z} ) ^Qj ^{( z} ) .

. z) Q( z) Pj( z)

Тогда, при соблюдении 2-го условия выходные сигналы полностью описывают передаточную матрицу системы.

Заключение

Таким образом, если система идентифицируема, то для ее описания достаточно использовать модель «вход-выход», при этом модель «вход-состояние-выход» является избыточной. Для слепой идентифицируемости линейной динамической системы, по крайней мере для случая дискретной системы с одним входом и множественным выходом, необходимо и достаточно выполнение двух условий: идентифицируемости системы в обычном смысле и отсутствие общих нулей полиномиальных компонентов передаточной матрицы системы.