Слепое разделение источников в задаче радиоконтроля с использованием нейронных сетей

В последние десятилетия бурно развивается одно из направлений цифровой обработки сигналов – слепая обработка сигналов. Одним из приложений таковой является анализ независимых компонентов, который решает проблемы слепого извлечения и разделения источников. Все чаще для решения подобных проблем прибегают к использованию нейронных сетей.

В статье рассмотрен информационно-теоретический подход к слепому разделению источников. В этом контексте в основе построения модели нейронной сети лежит принцип максимума взаимной информации Линскера [1].

Постановка задачи

Пусть s ( n ) случайный входной вектор, определенный следующим образом (рис. 1):

s(n) = [si (n),-, sm (n)]T , где m компонентов вектора выбираются из множества независимых источников, n – дискретное время. Вектор s применяется к линейной системе, характеристики отображения входа на выход которой задаются несингулярной матрицей смешения A размерности m * m . Результатом является вектор наблюдений:

x = As , где x = [xi ,-■-, xm ] .

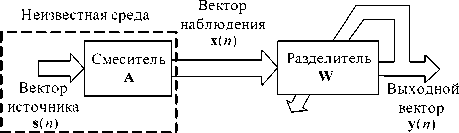
Рис. 1. Блочная диаграмма процессов для задачи слепого разделения источников

Вектор источника s и матрица смешения A считаются неизвестными. Для данного вектора x задача сводится к поиску разделяющей матрицы W такой, что исходный вектор s может быть получен из выходного вектора y , определяемого следующим образом:

y= Wx, где У = [ У1,-, Ут ]T .

При этом требуется, чтобы компоненты выходного вектора были статистически независимыми. Для определения меры статистической независимости выбирается взаимная информация I ( y i ; У j ) между случайными переменными yi и y _j , являющимися двумя компонентами выходного вектора y . Если эта взаимная информация равна нулю, то соответствующие компоненты y _i и являются статистически независимыми.

y _j ,

Этого можно добиться, минимизируя взаимную информацию между всеми парами случайных переменных, составляющих выходной вектор y .

Для решения задачи слепого разделения источников используется однослойная полносвязная нейронная сеть прямого прохождения, у кото- рой входной вектор x и выходной вектор y имеют одинаковые размерности. Задачей нейронной сети является настройка матрицы весов W таким образом, чтобы минимизировать статистическую зависимость между компонентами выходного вектора y . Матрица весов W будет искомой обратной матрицей для матрицы смешения A.

Алгоритм обучения нейронной сети разделению источников по принципу взаимной информации

Минимизация взаимной информации эквивалентна минимизации дивергенции Кулбека-Лей-блера между двумя следующими распределениями: функцией плотности вероятности f y ( y , W ) , параметризованной по W , и соответствующим факториальным распределением

m fy (y, W) = П fy (y, W), i=1

где f y ( y; , W ) - граничная функция плотности вероятности y _i .

Дивергенция Кулбека-Лейблера между плотностями распределения вероятностей f y ( y , w ) и f y ( y , w ) ^имеет вид

m

D ff ( W ) = - h ( y ) + - h ( y ) , i =1

где h ( y ) - энтропия случайного вектора на выходе разделителя сигнала; h ( y_t ) - граничная энтропия i -го элемента вектора.

Для определения граничной энтропии h(у ) используется приближенная формула в терминах моментов высокого порядка случайной переменной y _i .

Выражение для дивергенции Кулбека-Лейбле-ра поставленной задачи имеет вид [2]

D f | f ( W ) * - h ( x ) - log | det( W )| + у log(2 n e ) -

_ m^ ( ^K i ,3 + ^K i ,4 + ^{( K} i ,6 ^{+ 1} 0 ^K i ,3 )

-ill1 12    481440

— 8 ^K i ,3 ^K i ,4

-

^K i ,3 ( ^K i ,6 ^{+ 1} 0 ^K i, 3 ) _ ^K i , 4 ^{( k} i , 6 ^{+ 1 0 k} i ,3 ) _

• Ki,4 (Ki,6 + 10KУ )2 _ 524 _ (Ki,6 + 11)ку )3 ) 64         16432

где κ _i,k – семиинвариант k -го порядка случайной переменной y _i , являющийся функцией матрицы W .

Минимизация дивергенции Кулбека-Лейблера проводится методом градиентного спуска, в котором корректировке подвергается элемент w _i,k матрицы W :

^ w i , k = -n      Dy_f = n ( ^(W —T k ^- Ф ⁽ У ) x k ) ,

Swu f где η – скорость обучения, W-T – транспонированная обратная матрица для матрицы весов W, Ф(У1) — функция активации вида

1 5 2 7 15 9 2 11

ф ⁽ У1 ) = 2 У1 + з У1 + —yi + 15 У1 ^- 112             512

• -—У + 128 У¹⁵-— У 17 .

Корректировка для всей матрицы W :

A W = п ( W -T - ф ( y ) x ^T ) = n ( I - Ф ( y ) y T ) W ^-T , где Ф ( У ) = [ф ⁽ У 1 ),Ф ⁽ У 2 ) ■■■ Ф ⁽ У т )] T .

Правило коррекции при адаптации разделяющей матрицы имеет вид

W (n + 1) = W (n) + п (n) [ I - Ф ( У ) y T ] W -T (n) , где n – номер итерации.

Используя натуральный градиент [2], правило обучения можно переписать:

W (n + 1) = W (n) + n (n) [ l - ф ( y ) y T ] W (n) . (2)

Результаты моделирования

Моделирование проводилось в системе MATLAB.

Для слепого разделения источников используется модель однослойной полносвязной нейронной сети прямого прохождения с использованием алгоритма обучения (2). Число входов и выходов сети принимается равным двум – по числу полезных сигналов. Диаграмма процессов представлена на рис. 2.

Исходными сигналами являются: КАМ и ФМ сигналы. Они поступают на вход линейной смешивающей системы A . Затем к каждой смеси добавляется аддитивный гауссовский шум (для каждой смеси свой). Полезные сигналы модулированы на одной несущей, при этом мощность обоих сигналов одинакова.

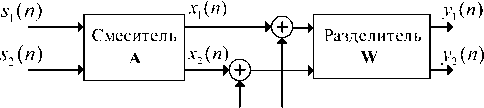
БГШ ₁ БГШ 2

Рис. 2. Блочная диаграмма процессов для задачи слепого разделения двух источников, смесь которых искажена аддитивным гауссовским шумом

Значения весов матрицы W перед началом обучения сети инициализируются случайными малыми значениями в диапазоне [0; 0,1]. Параметр скорости обучения был фиксированным и имел значение п = 0,1 ■ На выходе смесителя сигнал принимался с дискретизацией 50 Гц. Полезные сигналы имели частоту несущей 2 Гц. Длительность импульса была 2 с. Длина сообщения составляла 15 символов. Число итераций принималось равным 250.

Для количественной оценки эффективности разделителя был использован глобальный индекс отклонения, являющийся мерой диагональности матрицы P = WA :

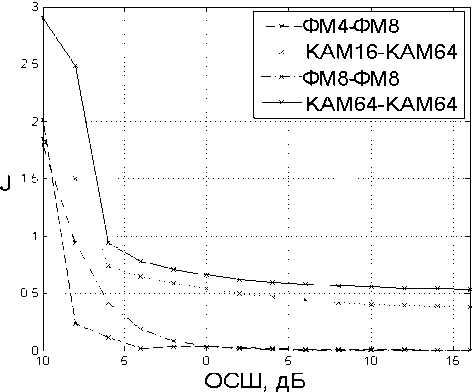
Рис. 3. Зависимость индекса отклонения от отношения сигнал-шум для комбинаций источников: ФМ4-ФМ8, КАМ16-КАМ64, ФМ8-ФМ8, КАМ64-КАМ64

mm

J = ∑ ⎜ ∑ i=1 ⎜_⎝ j=1

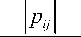
mkax pi

mm

+∑⎜⎜∑

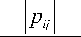
mkax pki

- 1

j=1

i=1

⎝

⎠

Если матрица P является диагональной, то J = 0 ■

Наилучший результат, характеризуемый малым значением индекса отклонения J , достигается при использовании сигналов с фазовой модуляцией. Большее значение J получается при использовании сигналов с разными видами модуляции (КАМ и ФМ). И, наконец, наибольшее значение J получается при использовании сигналов с КАМ.

Таким образом, чем меньше мера гауссовос-ти разделяемых сигналов, тем меньшее значение принимает индекс отклонения и тем быстрее сходится алгоритм.

Худшие результаты при использовании в качестве одного из сигналов сигнал с КАМ64 объясняются также тем, что 15 учебных символов (1500 отсчетов) недостаточно, чтобы получить достоверную оценку плотности распределения вероятностей для подобного случая, поскольку число возможных позиций составляет 64. Увеличить скорость сходимости можно, используя выборку с большим количеством учебных образцов.

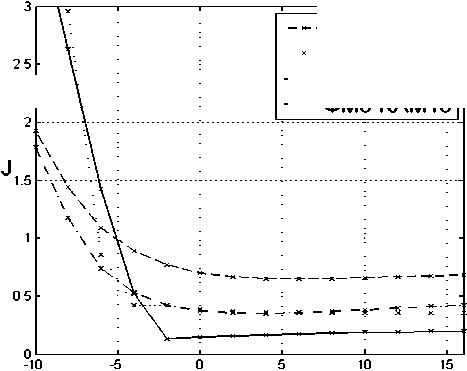
Графики зависимостей индекса отклонения от соотношения сигнал-шум изображены на рис. 3 и рис. 4. Эксперименты показали, что сходимость алгоритма имеет место при соотношении сигнал-шум, большим –5 дБ.

Отношение сигнал-шум рассчитывается по

P формуле ОСШ=101д —— ■

Pш

Как показали эксперименты, описанный алгоритм характеризуется малыми вычислительными затратами.

ОСШ, дБ

Рис. 4. Зависимость индекса отклонения от отношения сигнал-шум для комбинаций источников: ФМ4-КАМ64, ФМ8-КАМ64, ФМ4-КАМ16, ФМ8-КАМ16

ФМ 4-КАМ 64

ФМ8-КАМ64

— ФМ4-КАМ16

—ФМ 8-КАМ 16

Заключение

Исследование алгоритма разделения источников на основе взаимной информации показало, что разделение источников на фоне БГШ имеет место при малом значении соотношения сигнал-шум.

Разделение источников достижимо при использовании полезных сигналов, модулированных на одной несущей, а также при использовании одинаковых видов модуляции, например, ФМ8 и ФМ8.

Полученные результаты показали целесообразность применения нейронных сетей для слепого разделения источников в задаче радиоконтроля с использованием алгоритма обучения на основе взаимной информации.