Сложные режимы в модели миграционно связанных сообществ "хищник-жертва" с быстрыми и медленными циклами
Автор: Курилова Е.В., Кулаков М.П.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Биология. Математическое моделирование
Статья в выпуске: 1 т.22, 2019 года.
Бесплатный доступ
Исследуются режимы динамики, сочетающие быстрые и медленные изменения численностей в системе миграционно связанных сообществ «хищник-жертва» с лимитированием роста жертв и насыщением хищников. Описан режим, содержащий три разных цикла в фазовом пространстве, которые отличаются периодами колебаний, а также соотношением жертв на разных территориях и режимами синхронизации между хищниками. Появление такой динамики, вероятно, связано с «катастрофой голубого неба».
Сообщество, "хищник-жертва", миграция, синхронизация, "катастрофа голубого неба"
Короткий адрес: https://sciup.org/143167168
IDR: 143167168 | УДК: 574.34:517.925.42 | DOI: 10.31433/2618-9593-2019-22-1-12-19
Текст научной статьи Сложные режимы в модели миграционно связанных сообществ "хищник-жертва" с быстрыми и медленными циклами
Исследование динамики сообществ типа «хищник–жертва», «паразит–хозяин», «ресурс– потребитель» и т.п. является одним из центральных направлений математической популяционной биологии [9]. Неослабевающий интерес связан, прежде всего, с расширением области применения моделей динамики подобных сообществ. Например, актуальными являются эколого-эпидемиологические модели, которые описывают распространение инфекции в сообществах, взаимодействующих по принципу «хищник–жертва», в которых хищник с разной интенсивностью поедает больных и здоровых особей [15, 17]. Интересные результаты получены при описании пространственно-временной динамики в случае миграции хищников, которые следуют за перемещениями жертв (таксис) [3, 11, 20]. С другой стороны, вызывают особый интерес сложные нелинейные явления, наблюдаемые в математических моделях таких сообществ. В частности, исследуются условия синхронного или асинхронного поведения на разных территориях [6], механизмы возникновения странных, в том числе гомоклинических, аттракторов [2], закономерности формирования сложных пространственно-временных структур [11, 13] и др.
Ранее нами была предложена модель динамики двух миграционно связанных сообществ [5, 7]. Каждое рассматриваемое сообщество представляет собой систему типа «хищник–жертва» (именуемое подсистемой). Динамика каждого из сообществ описывается при помощи уравнений Базыкина [1]. То есть считается, что динамика численности жертв характеризуется ограниченным ростом, а число хищников в отсутствии жертв экспоненциально падает. Кроме того, число поглощенных или съеденных хищниками жертв и переработанных в собственную биомассу имеет насыщение. Другими словами, при низкой численности хищника или (и) жертв доля съеденных жертв растет быстрее, чем при высоких численностях. В иностранной литературе подобного рода зависимость известна как функциональный отклик Холлинга II типа [12]. В работах [5, 7] при исследовании этой модели основной акцент был сделан на изучении механизмов синхронизации периодической динамики двух неидентичных связанных подсистем при вариации параметра связи. Связь представляет собой симметричную миграцию хищников. Были описаны условия полной синхронизации динамики сообществ, а также ситуация, когда быстро растущее сообщество подавляет медленно растущее.
В настоящей же работе исследуются сложные режимы динамики, возникающие при частичной синхронизации динамики неидентичных сообществ на сопредельных территориях. Из-за разницы типичных времен эти режимы характеризуются сочетанием быстрых и медленных изменений численностей, а также различным соотношением синхронной и несинхронной динамики в отдельные временные периоды.
Модель динамики двух миграционно связанных сообществ
Рассмотрим используемые модельные уравнения. Обозначим через X 1, Y 1 и X 2, Y 2 соответственно общую численность популяции жертвы и хищника в первом и втором сообществах в момент времени t . Пусть оба сообщества обитают в схожих условиях и отличаются только максимальными скоростями размножения популяции жертвы, обозначенными a 1 и a 2 соответственно. При этом предполагается, что внутривидовая и межвидовая конкуренция не различается на разных территориях. Это отражает ситуацию, когда на сопредельных территориях существуют два разных вида жертв, имеющих одинаковую пищевую ценность для хищника.
Предполагается, что хищники могут мигрировать между сообществами, причем количество мигрантов из сообщества пропорционально численности хищника в этом сообществе. Коэффициенты пропорциональности (коэффициенты миграций) одинаковы для обоих сообществ, т.е. связь симметричная. Гибель особей в процессе миграции неявно включается в общую смертность. Внешние факторы, влияющие на развитие сообществ, не учитываются.
Таким образом, уравнения динамики численности двух миграционно связанных сообществ «хищник–жертва» в случае лимитирования роста жертв и насыщения числа поглощенных хищниками жертв имеют вид [5, 7]:
Xx = axXx K X 1
1 11 K
b X 1 Y 1
1 + AX 1
sXY
Y = - c Y +--+ m Y - m Y,
-
1 11 + AX1 21
X x K-X-
X 2 = a 2 X 2„
K
b X 2 Y 2
1 + AX 2
sXY
Y7 = - c Y , +-- 2—2— + mY - m Y,
-
2 2 1 + AX2 12
(1),
где K – устойчивая равновесная численность популяции жертв в каждом местообитании в отсутствии хищника, b – удельная скорость потребления популяцией хищника популяции жертвы при единичной плотности обеих популяций, c – естественная смертность хищника, s/b – коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу, A – коэффициент насыщения хищника, m – коэффициент миграции хищника.
Для уменьшения числа независимых параметров введем замену переменных: Xi ( t )= cx ( τ ) /s , Yi ( t ) =ay ( τ ) /b и характерного времени в каждой подсистеме: ti=τ/ai ( i =1, 2). В результате система уравнений (1) с восемью параметрами преобразуется к следующей системе с пятью параметрами:
x 1
= x 1
x 1 y 1 2
£x
-
1 + OXX
. yxxxux „ I yx y = -/1 y 1 + -:-----+ P /11 — y 2 - y 1
1 + 0x1
xy x7 = x7--2-^2— xx7
-
2 2 1 + ax 2
• /2 Х1У1 о I /2
У 2 = -/2 У 2 + , 2 2 2 + P Y 21 — У 1 - У1
1 + ax 2^
(2),
где α=Ac/s – новый коэффициент насыщения хищника, ε=c / Ks – коэффициент самолимитирования жертвы, γi=c/ai – относительная скорость снижения (убыли) численности хищников (смертности) и μi=βγi=m/ai ( β=m/c ) – коэффициент миграции хищников ( i =1, 2).
Несложно заметить, что такая замена приводит к тому, что два неидентичных сообщества, которые отличаются параметрами скорости роста жертв, оказываются неотличимы от сообществ, которые отличаются смертностью хищников. Кроме того, в системе (2) связь оказывается несимметричной и число особей, покинувших территорию (эмигрантов) и пополняющих другую (иммигрантов), неравно, что можно интерпретировать как присутствие смертности в ходе миграции. Причем диспропорция ( γ 1 /γ 2) между числом эмигрантов и иммигрантов растет (отлична от единицы) по мере роста различий в смертности хищников.
Необходимо заметить, что исследование систем дифференциальных уравнений традиционно состоит из вычисления особых точек или стационарных состояний, поиска условий их устойчивости, описания характерных бифуркаций, приводящих в частности к периодическим или сложным режимам динамики и др. Однако из-за сложного нелинейного вида уравнений (1) или (2) произвести полное их исследование крайне затруднительно. Вместе с тем несложно указать на существование следующих особых точек (без указания конкретных координат): тривиальная ( x 1 = 0, y 2 = 0, x 2 = 0, y 2 = 0 ) , несколько полу-тривиальных ( x 1 , y 1 ,0,0 ) , ( 0,0, x 2 , y 2 ) , ( 0, y 1 , x 2 , y 2 ), ( x 1 , y j ,0, y 2 ) и др. и, наконец, нетривиальная
( x 1 ,у 1 , x 2 , у 2 ) . Вопрос их устойчивости частично рассмотрен в [5]. В дальнейшем рассмотрим наиболее интересные сложные режимы динамики в системе (1) и укажем на бифуркационные механизмы их возникновения и трансформации.
Сложные режимы динамики
Выберем следующие значения параметров ε= 0,1, α= 0,5, при которых в каждой из подсистем, в случае их независимости ( β= 0), существуют предельные циклы с разными частотами, определяемыми значением параметров γi ( i =1, 2). Каждый из них возникает вокруг точки ( x 1 , у 1 ,0,0 ) или ( 0,0, x 2 , у 2 ) для первой и второй подсистем соответственно. Для удобства исследования зафиксируем значение скорости снижения численности хищников второго сообщества: γ 2 = 0,5. Предполагается, что эта территория с низкой скоростью роста численности жертв, что по характеру перехода от системы (1) к (2) эквивалентно высокой смертности хищников. В результате на второй территории формируется короткопериодичный цикл. Значение γ 1=0,002, напротив, невелико и на сопредельной территории сообщество демонстрирует длиннопериодичный цикл. Далее будем постепенно увеличивать значение скорости снижения численности хищников в первом сообществе γ 1. Это позволит проследить последовательность преобразований динамических режимов рассматриваемых сообществ.
В частности, обнаружено, что при небольших значениях коэффициента связи (0.001< β< 0,01) наблюдаются сложные режимы динамики, отмеченные в достаточно узком окне пространства параметров, и незначительная вариация значений одного из коэффициентов модели приводит к существенной перестройке динамики. Так, например, изменение значения параметра са-молимитирования жертвы ε влечет за собой серию динамических переходов от синхронного поведения двух связанных сообществ (предельного цикла) к абсолютно несинхронным режимам динамики (тор-хаосу).
Координаты точек u 1(0)=1,7, v 1(0)=6,5, u 2(0)=5,97, v 2(0)=1,16 примем в качестве начальных значений численностей каждой из рассматриваемых популяций. Эти значения соответствуют точкам на быстром и медленном предельных циклах, отмеченным для изолированных подсистем. Далее все численные эксперименты проводятся при следующих значениях параметров: α= 0,5, β= 0,0058, ε= 0,1, α= 0,5 и γ 2 = 0,5.
Продемонстрируем некоторые обнаружен- ные режимы.
При малых значениях коэффициента скорости убыли хищников ( γ 1 < 0,003) вокруг полу-тривиального равновесия ( x 1 , у 1 ,0, у 2 ) существует асимптотически устойчивый предельный цикл. Это состояние, как и предельный цикл, реализуемый вокруг него, соответствует ненулевой численности жертвы в первом сообществе ( Х 1 > 0) и ее полному отсутствию во втором ( x 2 = 0) (рис. 1).
Таким образом, видно, что наличие на одной из территорий более сильного сообщества (с высокой скоростью воспроизводства жертв или высокой смертностью хищника) приводит к тому, что оно ожидаемо подавляет более слабое. При этом жертвы второго сообщества уничтожаются хищниками практически полностью (их численность стремится к нулю). В этом случае численность жертв в первой популяции в несколько раз превышает численность хищников. Причем максимум численности жертвы приходится на минимум хищников обоих сообществ (рис. 1б), это указывает на то, что всплеск рождаемости жертвы возможен во время наиболее сильного снижения числа хищников. И наоборот, при достижении хищниками своей максимальной численности число жертв резко падает (стремится к нулю). На трехмерной проекции траектории системы (2) это отражается в виде предельного цикла (рис. 1а), нижняя часть которого лежит в плоскости ( y 1, y 2), а сам предельный цикл целиком реализуется в инвариантном подпространстве ( x 1, y 1, y 2).
Интересно, что отсутствие жертв во втором сообществе не препятствует перемещению хищников между сопредельными территориями в поисках пищи. В этом случае предельный цикл вокруг точки ( x 1 , у 1 ,0, у 2 ) целиком лежит на плоскости у 1 =у 2 , т.е. динамика численностей хищников на обеих территориях оказывается полностью синхронной или близка к ней. Это указывает на «особую» роль второй территории, на которой хищники присутствуют лишь за счет иммиграции, а, естественно, воспроизводство за счет потребления жертв там невозможно.
Вместе с устойчивым предельным циклом вокруг точки ( x 1 , у 1 ,0, у 2 ) существует седловой цикл вокруг нетривиальной точки ( x 1 , у 1 , x 2 , у 2 ) . Далее в результате последовательности седло-узловой и суперкритической бифуркации Андро-нова-Хопфа (при γ 1 ≈ 0,0031) формируется новый цикл, который содержит оба этих цикла (рис. 2). Это проявляется в том, что траекторию с медлен-
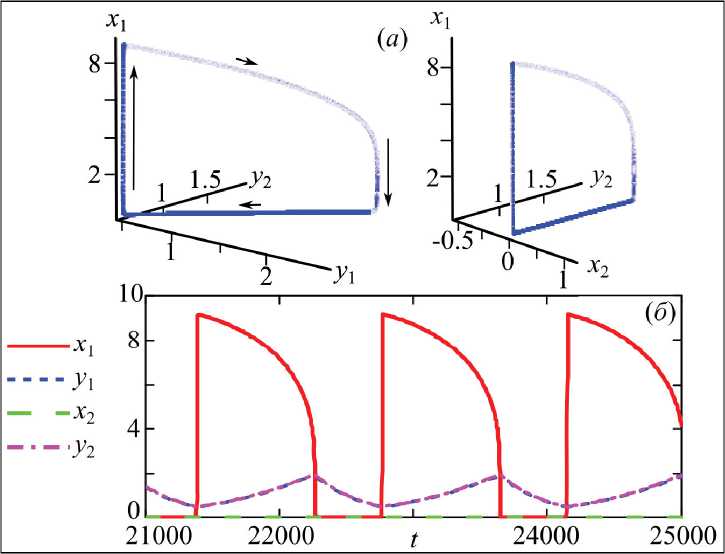
Рис. 1. а – трехмерные проекции траектории системы (2) и б – динамика численности жертв и хищников на обеих территориях при γ1=0,0028, значение остальных параметров указано в тексте. Стрелки указывают направление движения вдоль фазовой кривой, длина соответствует скорости изменения численностей (длинные – быстро, короткие – медленно)
Fig. 1. а – three-dimensional projections of the system’s (2) trajectory and б – the dynamics of pray and predators in both territories at γ1=0,0028, the value of other parameters is shown in the text above.
The arrows indicate the movement along the trajectory; their length corresponding to the rate of numbers change (long for fast, and short for slow)
ного цикла (с большим периодом) вокруг первой полутривиальной точки ( x 1 , у 1 ,0, у 2 ) начинает притягивать к быстрому циклу (с небольшим периодом) вокруг нетривиальной точки ( x 1 , у 1 , x 2 , у 2 ) . Эта точка и цикл в ее окрестности соответствуют одновременному существованию всех популяций (рис. 2а).
Переход к быстрому (пачечному) режиму сопровождается появлением ранее отсутствовавших на второй территории жертв, число которых оказывается много меньше жертв на первой территории (с высокой скоростью воспроизводства) (рис. 2б). Динамика на второй территории при этом демонстрирует затухающие колебания, а численность хищников синхронно следует за изменением числа жертв до момента полного их уничтожения на второй территории (рис. 2в). После чего модельная траектория возвращается на медленный цикл (тонический режим). Другим словами, после почти полного уничтожения жертвы второго сообщества хищники перемещаются на сопредельную территорию и участвуют в поедании жертвы первого сообщества до практически полного ее уничтожения. В результате в определенные моменты времени жертвы в обоих сообществах практически отсутствуют, а число хищников монотонно и с одинаковым темпом падает. На трехмерной проекции модельной траектории (рис. 2а) данный довольно большой временной отрезок соответствует части траектории, лежащей в плоскости y1=cy2 (c≈1). При достижении определенной критической численности хищников траектория с тонического вновь переходит на быстрый пачечный режим вокруг нетривиальной точки (x1, у1, x2, у2) и режим повторяется.
Можно отметить, что описанное динамическое поведение сочетает в себе как быструю колебательную или пачечную динамику с ненулевыми численностями хищников и жертв на обеих территориях, так и медленную тоническую динамику, соответствующую почти нулевой численности жертв на второй территории. Кроме того,
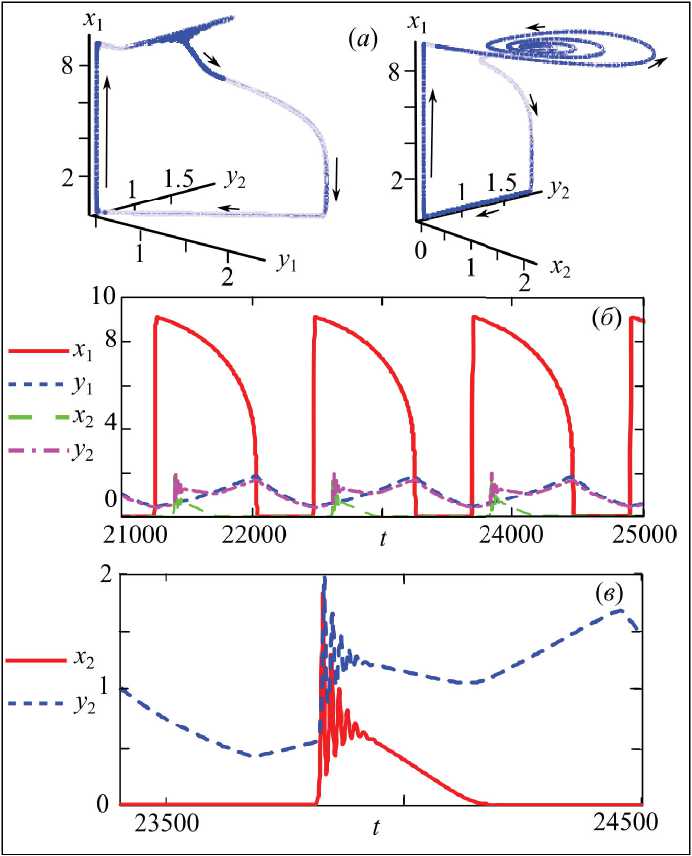
Рис. 2. а – трехмерные проекции траектории системы (2), б – динамика численности хищников и жертв на обеих территориях, в – динамика второго сообщества при γ1=0,0031
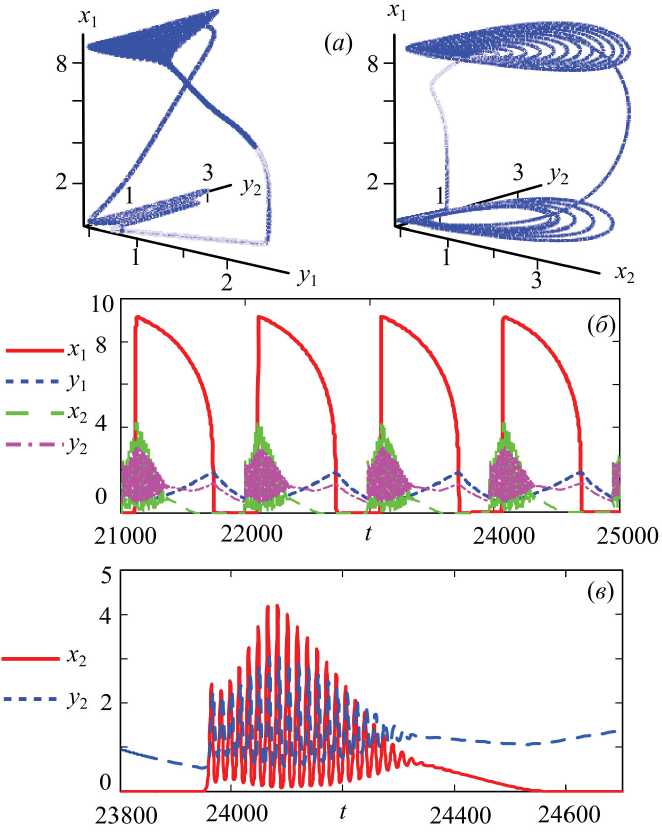
Рис. 3. а – трехмерные проекции траектории системы (2), б – динамика численности хищников и жертв на обеих территориях, в – динамика второго сообщества при γ1=0,004
Fig. 2. а – three-dimensional projections of the system’s trajectory (2), б – the dynamics of pray and predators in both territories, в – the second community dynamics at γ1=0.0031
переход между двумя этими циклами оказывается очень быстрым (взрывным). По всей видимости, подобный тип динамики в системе (2) возникает в результате «катастрофы голубого неба», описанной и изученной в работах Л.П. Шильникова, А.Л. Шильникова и Д.В. Тураева [8, 19]. Эта бифуркация позволяет, в частности, объяснить наблюдаемый для ряда биологических систем тип динамики, содержащий быстрые всплески, периоды быстрых колебаний с большим размахом, которые чередуются периодами медленной ровной динамики и т.п. Это, например, работы, связанные с изучением нейронной и клеточной активности [4, 10, 18], а также исследованием систем типа «ресурс-потребитель» (лес и растительноядные насекомые) [14, 16] и др. По аналогии с некоторыми цитируемыми работами далее будем называть описанную динамику «траекторией голубого неба».
Дальнейшее изменение параметра убы-
Fig. 3. а – three-dimensional projections of the system’s trajectory (2) б – the dynamics of pray and predators in both territories, в – the dynamics of second communities at γ1=0.004
ли хищника на первой территории до значения γ 1 = 0,004 приводит к существенной перестройке характера колебаний (рис. 3). Так, после полного уничтожения хищниками жертв первого сообщества траектория с цикла вокруг точки ( x 1 , у 1 ,0, у 2 ) притягивается к новому циклу вокруг третьей точки ( о, у 1 , x 2, у 2 ) , которая соответствует отсутствию жертвы, на этот раз в первом сообществе, а затем к циклу вокруг нетривиального равновесия ( x 1 , y 1 , x 2 , y 2 ) *
В этом случае характер колебаний и форма пачки претерпевают значительные изменения. Например, в предыдущем примере после перехода с пачечного на тонический режим численность хищников и жертв на второй территории очень быстро достигала максимальных значений, после чего следовали затухающие колебания, а пачка имела треугольную форму (рис. 2в). Причем это происходит только после восстановления жертв на первой территории (рис. 2б). В данном же случае после выхода на быстрый режим жертвы сначала восстанавливаются на второй территории, а только после этого на первой. При этом случае периодическая траектория концентрируется вокруг точки (0, у1, X2, у2), а колебания какое-то время раскачиваются до максимальной амплитуды в пачке. Затем, после того как жертвы восстанавливаются на первой территории, траекторию перебрасывает в окрестность точки (X1, у1, x2, у2) и колебания сменяются затухающими. В результате пачка имеет усеченную ромбовидную форму (рис. 3в). Таким образом, образуется два колебательных пачечных режима, соединенных между собой тоническим, что приводит к своего рода «удвоению» траектории голубого неба (рис. 3а). В данном случае тонический режим соответствует периоду времени, необходимому для полного восстановления жертв на обеих территориях или, соответственно, для их почти полного уничтожения.
Данный сценарий, наблюдаемый при более высоких значениях γ 1, интересен тем, что жертвы по-прежнему могут отсутствовать на обеих территориях, но заметно менее продолжительное время. С одной стороны, это проявляется в том, что восстановление популяции жертв на второй территории происходит раньше, чем на первой. С другой, наблюдается более ранний выход на пачечный режим и увеличивается размер пачки, т.е. растет число витков вокруг точки ( X 1 , у 1 , x 2, у 2 ) . Переход между пачечным и тоническим режимами может быть резким, как, например, при γ 1 = 0,004 (рис. 3), либо относительно медленным, как, например, при γ 1 = 0,005 (рис. 4). В последнем случае траектория «медленно» переходит из окрестности точки ( 0, у 1 ,0, у 2 ) в окрестность ( 0, у 1 , X 2 , у 2 ) и формируются раскачивающиеся колебания численности жертв и хищников на второй территории, которые сменяются затухающими, после того как траектория оказывается рядом с нетривиальной точкой ( X 1 , у 1 , X 2 , у 2 ) . В результате пачка приобретает ромбовидную окрестность (рис. 4в).
Важно отметить, что динамика хищников на разных территориях с ростом параметра убыли хищника становится менее синхронной, чем в случае «простой» траектории голубого неба. Например, при γ 1 < 0,005 в тонической части траектория частично лежит в плоскости y 1 =qy 2 ( q> 0). Уже при γ 1 ≥ 0,005 синхронизация нарушается и на тонической части траектории динамика хищников оказывается несинфазной. Причем сразу после
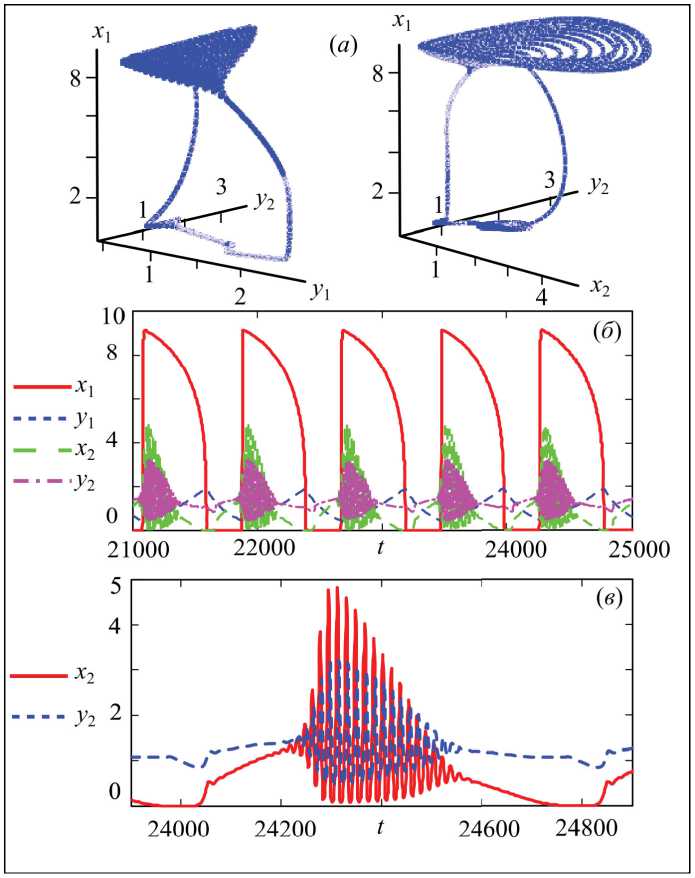
Рис. 4. а) – трехмерные проекции траектории системы (2), б – динамика численности хищников и жертв на обеих территориях, в – динамика второго сообщества при γ1=0,005
Fig. 4. а – three-dimensional projections of the system’s trajectory (2), б – the dynamics of pray and predators in both territories, в – the dynamics of second communities at γ1=0.005
выхода с пачечного режима число хищников монотонно падает и точки в фазовом пространстве частично лежат на плоскости y 1 =qy 2 ( q> 0). После чего траекторию притягивает к циклу в окрестности точки ( 0, у 1 ,0, у 2 ) и динамика хищников оказывается противофазной, а траектория лежит на плоскости y 1 =w – vy 2 ( w> 0, v> 0).
Заключение
Таким образом, в системах двух связанных неидентичных сообществ «хищник–жертва» обнаружена периодическая динамика, которая содержит быстрые и медленные периодические изменения численности (циклы), названные траекторией голубого неба. Причем по отдельности каждый из этих циклов соответствует разным соотношениям хищников и жертв на сопредельных территориях. При медленных движениях второе, более слабое сообщество (с высокой смертностью хищников или низкой рождаемостью жертв), полностью по- давляется первым. При быстрых движениях можно выделить периоды времени, когда оба сообщества сосуществуют. Обнаружено, что в разных частях этого сложного цикла динамика хищников и жертв может содержать как синхронные, так и асинхронные участки. Последние наблюдаются в тот момент, когда траекторию голубого неба «втягивает» новый быстрый цикл, соответствующий короткому периоду превалирования слабого сообщества над сильным (с низкой смертностью хищников или высокой скоростью роста жертв). По всей видимости, это возможно до тех пор, пока сильное сообщество не успело восстановиться.
Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН и частичной финансовой поддержке РФФИ (проект № 1851-45004 ИНД_а).
Список литературы Сложные режимы в модели миграционно связанных сообществ "хищник-жертва" с быстрыми и медленными циклами
- Базыкин А.Д. Математическая биофизика взаимодействующих популяций. М.: Наука, 1985. 182 c
- Баханова Ю.В., Казаков А.О., Коротков А.Г. Спиральный хаос в моделях типа Лотки-Вольтерры//Журнал средневолжского математического общества. 2017. Т. 19, № 2. С. 13-24 DOI: 10.15507/2079-6900.19.201701.013-024
- Говорухин В.Н., Моргулис А.Б., Тютюнов Ю.В. Медленный таксис в модели «хищник-жертва»//Доклады Академии наук. 2000. Т. 372, № 6. С. 730-732
- Коломиец М., Шильников А. Методы качественной теории для модели Хиндмарш-Роуз//Нелинейная динамика. 2010. Т. 6, № 1. С. 23-52 DOI: 10.20537/nd1001003
- Курилова Е.В. Синхронизация колебаний в динамике численности двух миграционно связанных сообществ «хищник-жертва»//Региональные проблемы. 2014. Т. 17, № 2. С. 35-39
- Курилова Е.В., Кулаков М.П. Условия синхронизации численности двух взаимосвязанных сообществ (на основе модели Лотки-Вольтерра)//Региональные проблемы. 2014. Т. 17, № 1. С. 5-8
- Курилова Е.В., Кулаков М.П., Фрисман Е.Я. Последствия синхронизации колебаний численностей в двух взаимодействующих сообществах типа «хищник -жертва» при насыщении хищника и лимитировании численности жертвы//Информатика и системы управления. 2015. Т. 45, № 3. С. 24-34
- Тураев Д.В., Шильников Л.П. О катастрофах голубого неба//Доклады АН СССР. 1995. Т. 342, № 5. С. 596-599
- Фрисман Е.Я., Кулаков М.П., Ревуцкая О.Л., Жданова О.Л., Неверова Г.П. Основные направления и обзор современного состояния исследований динамики структурированных и взаимодействующих популяций//Компьютерные исследования и моделирование. 2019. Т. 11, № 1. С. 119-151
- Belykh V.N., Belykh I.V., Colding-Jørgensen M., Mosekilde E. Homoclinic bifurcations leading to the emergence of bursting oscillations in cell models//Eur. Phys. J. E. 2000. N 3. P. 205-219
- Comins H.N., Hassell M.P., May R.M. The spatial dynamics of host-parasitoid systems//J. Animal Ecology. 1992. Vol. 61. P. 735-748. 10.2307/5627
- DOI: :10.2307/5627
- Holling, C. S. Some characteristics of simple types of predation and parasitism//Canadian Entomologist. 1959. Vol. 91. P. 385-398
- DOI: 10.4039/Ent91385-7
- Huang T., Zhang H. Bifurcation, chaos and pattern formation in a space-and time-discrete predator-prey system//Chaos, Solitons & Fractals. 2016. Vol. 91. P. 92-107
- DOI: 10.1016/j.chaos.2016.05.009
- Khibnik A.I., Kondrashov A.S. Three mechanisms of Red Queen dynamics//Proceedings of the Royal Society of London. Series B: Biological Sciences. 1997. Vol. 264. P. 1049-1056
- DOI: 10.1098/rspb.1997.0145
- Mukhopadhyay B., Bhattacharyya R. Role of predator switching in an eco-epidemiological model with disease in the prey//Ecological Modelling. 2009. Vol. 220, N 7. PP. 931-939
- DOI: 10.1016/j.ecolmodel.2009.01.016
- Rinaldi S., Muratori S. Slow-fast limit cycles in predator-prey models//Ecological Modelling. 1992. Vol. 61. P. 287-308
- Saifuddin Md., Biswas S., Samanta S., Sarkar S., Chattopadhyay J. Complex dynamics of an eco-epidemiological model with different competition coefficients and weak Allee in the predator//Chaos, Solitons & Fractals. 2016. Vol. 91. P. 270-285
- DOI: 10.1016/j.chaos.2016.06.009
- Shilnikov A. Cymbalyuk G. Homoclinic bifurcations of periodic orbits en a route from tonic-spiking to bursting in neuron models//Regular and Chaotic Dynamics. 2004. Vol. 9, N 3. P. 281-297
- DOI: 10.1070/RD2004v009n03ABEH000281
- Shilnikov A., Shilnikov L., Turaev D. Blue-sky catastrophe in singularly perturbed systems//Moscow Mathematical Journal. 2005. Vol. 5, N 1. P. 269-282
- Tyutyunov Yu.V., Titova L.I., Senina I.N. Prey-taxis destabilizes homogeneous stationary state in spatial Gause-Kolmogorov-type model for predator-prey system//Ecological Complexity. 2017. Vol. 31. P. 170-180


