Случайность и пространственная коррелированность размещения разнотипных геологических объектов в пространстве. Часть 2: метод потенциалов взаимного влияния

Предварительный анализ1 показал, что пока не существует удовлетворительного метода оценки пространственной коррелированности точек-объектов отличающихся типов. Имеющиеся варианты основаны на учете расположения ближайших точек или точек, совместно попадающих в достаточно малые пространственные ячейки. Критерии, основанные на этой ничтожно малой доле информа ции, не могут быть эффективными при проверке статистических гипотез, в нашем случае — при проверке гипотезы независимости размещения типов точек и оценке меры их пространственной зависимости, если она имеется.

В основу предлагаемого метода положены следующие принципы: 1) должна использоваться вся имеющаяся информация (т. е. координаты всех точек всех типов); 2) потенциал влияния — величина положительная и убывающая при увеличении расстояния между парой разнотипных точек; 3) потенциал влияния, создаваемый множеством точек одного типа на множество точек другого типа, — величина аддитивная; 4) потенциал влияния — величина нормированная (т. е. не зависящая от числа точек одного и другого типов); 5) область рас-

пространения точек одного и другого типов должна быть оконтурена, быть единой и определяться природой типов точек (как правило, должен охватываться возрастной интервал, формационный или фациальный тип отложений); 6) при выборе t = степени обратного расстояния в выражении 1/r t мы руководствовались законом ослабления действия в однородном изотропном пространстве. На плоскости, т. е. при D = 2, это закон зависимости увеличения длины окружности от её радиуса, т. е. t = D — 1 = 1; в реальном физическом пространстве это площадь сферы, увеличивающаяся пропорционально квадрату радиуса сферы, т. е. t = D — 1 = 3 — 1 = 2. Для пространств больших размерностей по аналогии также принимаем t=D— 1. Здесь наблюдается аналогия с зако ном всемирного тяготения, в знаменателе которого стоит квадрат расстояния, и законом изменения «концен трационного» потенциала источников компонентов в химии, освещенности вокруг светящихся тел и т. д.

Таким образом, потенциал влияния множества влияющих точек численностью N 1 (назовем их первым типом) на множество испытывающих влияние точек численностью N , (второй тип) рассчитывается для двухмерного пространства по формуле:

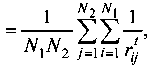
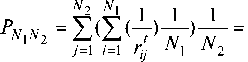
где t = 1. Если поменять местами смысл множеств точек N 1 и N ₂, т. е. влияющими считать точки N , , а находящимися под влиянием точки N ₁, то формула (1) перепишется следующим образом:

N2Nv

-§^4'

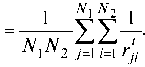
т. е. получим PNxN^ = Т^, так что формулы (1) и (2) отличаются только порядком суммирования и нормирования. Каждое слагаемое остается прежним, как и их число. Точки обоих типов в этом отношении симмет ричны.

Проиллюстрируем это конкретным примером (рис. 1, таблица). Он подтверждает тождественность результатов: потенциал влияния множества N 1 точек одного типа на множество N , точек «другого» типа есть то же самое, что и потенциал влияния множества точек N ₂ «другого» типа на множество N 1 точек первого типа. Как и следовало ожидать, ситуация симметрична по отношению к обоим типам точек. В обоих вариантах расчета потенциал оказался равным 3.398. Забегая вперед, отметим, что это значение статистически значимо превышает то, которое следует при случайном независимом размещении типов точек, а именно 2.977, полученное многократным компьютерным моделированием по 100000 раз.

Этот результат на первый взгляд может показаться подозрительным. Однако более внимательное рассмотрение рисунка показывает, что точки обоих типов тяготеют к средней части возможной области размещения точек единичного квадрата, а привершинные (угловые) участки не содержат точек ни первого, ни второго типов. При анализе «на глаз» этот факт ускользает от внимания.

Особого рассмотрения требует одномерный случай распределения точек на линии, т. е. при D = 1, когда t = D — 1 = 0. Потенциал влияния в этом случае будет равен:

Пример расчета потенциалов влияния друг на друга двух типов точек ( N ₍ = 3, N ₂ = 2)

Пары точек                    Координаты                 Расстояния „                         Черные __ Белые _______ в парах Черные    Белые      х        у        х        у          г	Обратные расстояния -1 и потенциалы
1           1         0.175      0.750      0.350      0.450        0.347 1           2        0.175      0.750      0.518      0.750        0.350 2           1         0.575      0.587      0.350      0.450        0.263 2          2        0.575      0.587      0.518      0.750        0.169 3           1         0.775      0.460      0.350      0.450        0.425 3           2        0.775      0.460      0.518      0.750        0.388	2.882 2.857 3.802 5.917 2.352 2.577
Нормированный по числу черных точек потенциал в белой точке 1	(2.882+3.802+2.352)73=3.012

(создается черными точками 1,2, 3)

Нормированный по числу черных точек потенциал в белой точке 2 (создается черными точками 1,2, 3)	(2.857+5.917+2.577)73=3.784
Средний потенциал в белых точках	(3.012+3.784)72=3.398
Нормированный по числу белых точек потенциал в черной точке 1 (создается белыми точками 1,2)	(2.882+2.857)72=2.869
Нормированный по числу белых точек потенциал в черной точке 2 (создается белыми точками 1,2)	(3.802+5.917)72=4.859
Нормированный по числу белых точек потенциал в черной точке 3 (создается белыми точками 1,2)	(2.352+2.577)72=2.464
Средний потенциал в черных точках	(2.869+4.859+2.464)73=3.397

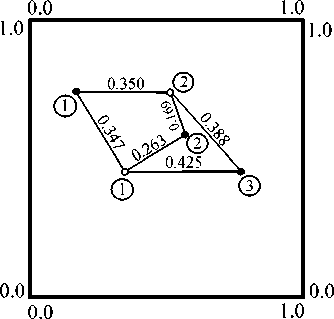
Рис. 1. Исходные данные для расчета потенциалов взаимного влияния (см. таблицу) в пределах единичного квадрата. Подписи на линиях — расстояния между точками в долях стороны квадрата. Расчетные потенциалы влияния равны 3.3975, что сильно превышает теоретическое значение 2.977 для независимого размещения типов точек из-за того, что оба типа точек на рисунке отсутствуют в угловых областях и в нижней части квадрата

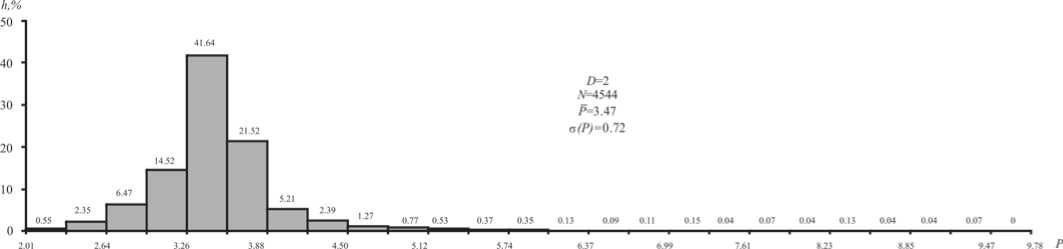
Рис. 2. Гистограмма нормированного потенциала влияния совокупности N случайно размещенных в единичном квадрате точек

на точку в центре этого квадрата

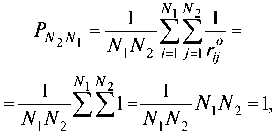
т. е. независимо от варианта размещения точек обоих типов, случайного или пространственно коррелированного, потенциал влияния будет постоянной величиной, равной единице. Это согласуется с интуитивным представлением ситуации в терминах силовых линий: они не «рассеиваются» по сторонам, так как «других сторон», кроме как единственной линии, в одномерном случае не существует. Отсюда следует вывод, что для одномерного случая понятия пространственной коррелированности не существует.

Итак, введенная мера зависимости — потенциал влияния — более точно должен быть назван нормированным потенциалом взаимного влияния типов точек .

С помощью компьютерного моделирования нами прежде всего исследовалась функция распределения потенциала влияния N случайно размещенных точек одного типа на пробную точку другого типа, перемещаемую по плотной сети в пределах изучаемой области пространства. Обычно этой областью был единичный квадрат в пространстве D = 2. Площадное распределение потенциала PN 1 образует поверхность со следующими особенностями. «Низины» поверхности располагаются на участках, где отсутствуют влияющие точки, имеют очень пологий «рельеф» без крутых участков. Поднятия («вершины»), напротив, круто поднимаются к местам расположения каждой влияющей точки (как сталагмиты на полу пещер) и образуют точечные сингулярности с бесконечным значением потенциала, так как знаменатель од ного из его слагаемых (расстояние до ближайшей точки) в этих случаях равен нулю. Эти особенности определяют вид эмпирической функции распределения потенциала: отсутствие нулевых значений, быстрое нарастание плотности в левой части кривой распределения, очень длинный правый «хвост» с очень малыми и неустойчивыми частотами. Аналогичный вид имеет распределение потенциала влияния большого числа случайно размещенных точек на фиксированную пробную точку, располагающуюся, например, в центре единичного квадрата (рис. 2).

Большая серия моделирований была посвящена изучению влияния на распределение потенциала численностей точек N । и N , . Распределение этого нормированного потенциала оказывается также правоасимметричным, причем коэффициент асимметрии уменьшается с увеличением численности пар точек, образуемых множествами N 1 и N , (см. рис. 3 и 4).

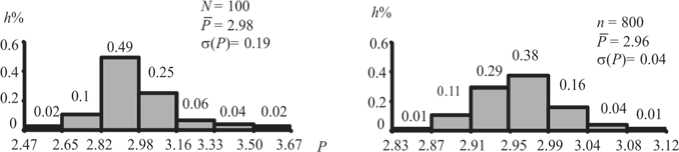
Рис. 4. Гистограммы нормированного потенциала взаимного влияния случайно и независимо размещенных двух типов точек суммарной численностью N = 50, 100, 200,400, 800,1600 при случайном соотношении долей типов

Особенно подробно моделировалось распределение потенциала влияния при случайном размещении точек первого и второго типов с различными комбинациями их абсолютных численностей и соотношений типов. При этом выяснилось, что среднее значение потенциала, нормированного на число пар, исключительно устойчиво (2.98) и не зависит по отдельности ни от количества точек первого и второго типов,

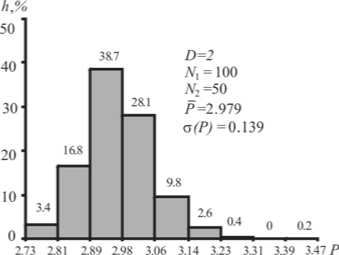
Рис. 3. Гистограмма частостей нормированного потенциала взаимного влияния (P) совокупностей точек двух типов численностью N 1 и N ₂

ни от их соотношения. Это позволяет использовать данный показатель (среднее значение потенциала) в качестве критерия для диагностики независимости друг от друга размещения типов точек. Если его среднее значение статистически незначимо отличается от 2.98, то размещение типов точек независимо; если превышает это значение, то типы коррелируют положительно; если меньше его, то отрицательно .

Наглядное представление о взаимном расположении двух типов положительно или отрицательно коррелирующих точек дает рис. 5. В верхней части рисунка изображен разрез «рельефа» поля потенциала влияния Р некоторого количества точек первого типа в проекции на «вертикальную» плоскость, перпендикулярную плоскости единичного квадрата, который является пространством с D = 2.

Этот «рельеф» усеян пиками-сингулярностями расположения точек с крутыми спусками, повторим, как у сталагмитов в пещерах. Пространства между пиками представляют собой пологие впадины, которые имеют разную глубину в зависимости от удаленности от неё точек — источников потенциала.

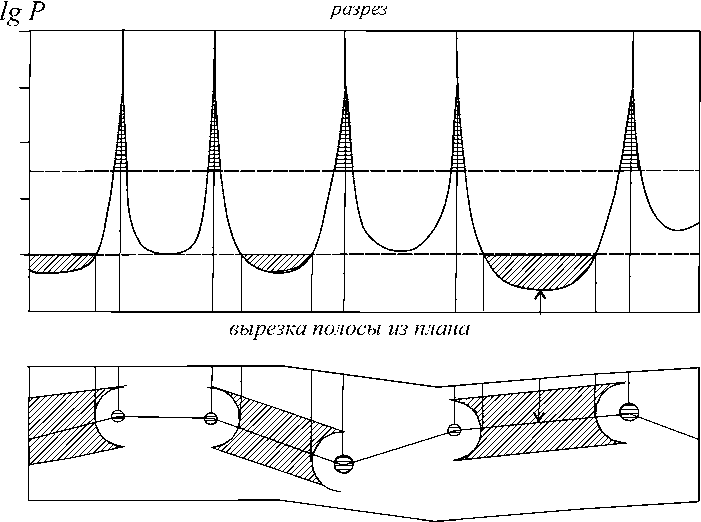
Рис. 5. «Рельеф» потенциала влияния точек преобладающего типа по ломаной линии, соединяющей близкие к разрезу точки, в проекции на плоскость чертежа. «Пики» — сингулярности потенциала влияния при полном совпадении координат точек первого и второго типов (Р ^ да ), что теоретически и практически невозможно. Горизонтальной штриховкой показаны области расположения точек второго типа при сильной положительной пространственной коррелированности их с точками первого типа. Косой штриховкой показаны области расположения точек второго типа при умеренной отрицательной пространственной их коррелированности с точками первого типа. Стрелкой указано положение воображаемой точки второго типа с минимальным потенциалом влияния на нее совокупности точек первого типа. Двухмерное пространство

При случайном и независимом от точек первого типа размещении точек второго типа средний потенциал взаимного влияния будет равен для двухмерного пространства 2.98. При положительной коррелированности это значение будет выше, а точки второго типа будут располагаться преимущественно в областях, заштрихованных горизонтально, при отрицательной коррелированности — в основном в области с косой штриховкой, т. е. во впадинах рельефа потенциала.

Изложенное позволяет моделировать расположение точек, удовлетворяющее заданной степени коррелированности. Если требуется положительная коррелированность, следует задаться некоторым большим критическим значением потенциала P, получать случайные координаты точки, рассчитывать для неё потенциал (зависящий от положения), и если он оказывается меньше, чем Pкр, то полученная точка второго типа отбрасывается, в противном случае принимается. И в том и в другом случае число попыток Nп наращивается на единицу. По достижении заданного числа точек второго типа N2 высчитывается величина 1 - -^, которая принимается за показатель степени положительной коррелированности. Действительно, чем большим значением задана величина Pкр, тем меньшей оказывается площадь, в которую должна попасть моделируемая точка, тем больше оказывается степень коррелированности. При Pкр=0 будет всегда N, =Nп, а степень коррелированности равна нулю.

При моделировании отрицательной коррелированности P _кр следует задавать достаточно малым, а «фильтрацию» точек проводить так, чтобы отбрасывались точки, для которых P > P _кр. Показатель коррелированности

• 1--- меняется от нуля при N_n = N , до

• 1 при N n ^ ~. Это не совсем удобно.

Традиционно коэффициенты дают более наглядное представление о явлениях, когда их значения изменяются от —1 до +1 и имеют нулевое значение при отсутствии влияния (зависимости). Таким коэффициентом в нашем случае является коэффициент R , где

1 N

К -\    - , Е-‘ h --2-,   (3)

причем знак коэффициента определяется величиной среднего потенциала взаимного влияния, а именно:

-1 если Р > P_D

sign(R) = < О

если Р = P_D

+ 1 если Р < P_D,

где P_D — среднее значение нормированного взаимного потенциала влияния для пространства размерностью D , sign(R) — знак числа, т. е. 1, — 1 или 0.

Исследование пространственной коррелированности типов точек производится в следующем порядке. По координатам точек заданного примера численностью N ₁ и N , в соответствии с формулой (1) по расчетной схеме, представленной в таблице, рассчитывается средний нормированный эмпирический потенциал взаимного влияния Р_э .Дё Для этого же числа точек многократно моделируется случайное (независимое) расположение N ₁ точек первого типа и N ₂ точек второго типа. По каждому моделированию по такой же схеме рассчитывается значение Р_{с N N} при случайном размещении типов точек. Моделирование повторяется несколько тысяч

раз, чтобы получить устойчивую гистограмму значений Р_с ^ По гистограмме строится доверительный интервал для математического ожидания потенциала с заданным уровнем значимости, как указано в части 1. Если потенциал Р_{э N}^_N^ для изучаемого примера укладывается в построенный доверительный интервал для случайно размещенных совокупностей точек N 1 , N 2 , то нулевая гипотеза об отсутствии пространственной коррелированности типов точек не отклоняется и исследование на этом заканчивается.

Обратим внимание, что вывод о наличии пространственной коррелированности типов точек делается на основе компьютерного моделирования распределения потенциала взаимного влияния в условиях истинности нулевой гипотезы N_o — отсутствия коррелированности для множеств N 1 и N 2 типов точек в пространстве размерности внутри заданного задачей контура размещения точек . Современные рядовые компьютеры позволяют осуществить проверку такой гипотезы за несколько секунд, что быстрее, чем поиск таблиц распределения критерия, если бы они существовали. Но их нет, во-первых, ввиду теоретической сложности проблемы, во-вторых, ввиду огромного разнообразия данных по численности точек, по соотношению количества типов, по бесконечному разнообразию контуров размещения точек.

Если нулевая гипотеза (об отсутствии коррелированности типов точек) отклоняется, естественным образом возникает задача расчета доверительных интервалов для коэффициента пространственной коррелированности . Обратимся к номограммам на рис. 6, 7. Они получены, как описано выше, моделированием случайных координат N 1 точек превалирующего типа ( N 1 >  N ₂), затем «поштучным» моделированием случайных координат точки второго типа с последующим расчетом потенциалов взаимного влияния P со множеством точек превалирующего типа и отбрасыванием этой точки, если P окажется больше P _кр. Процесс «поштучного» моделирования заканчивается по достижении необходимого количества точек N 2 .

Процесс моделирования N2 точек повторяется при увеличении Pкр (уменьшении при отрицательной коррелированности) с выбранным igP 2.01

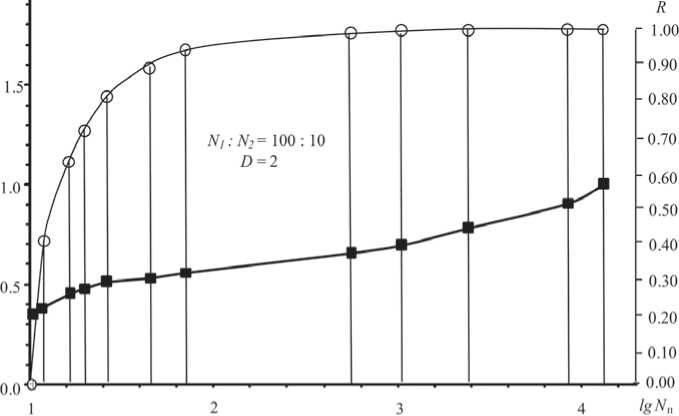
Рис. 6. Номограмма, связывающая критические значения потенциала взаимного влияния Р_кр (Р_кр >  2.98, линия квадратиков) со средним потенциалом взаимного влияния (левая шкала ординат, масштаб логарифмический) и с коэффициентом пространственной коррелированности типов точек (линия кружков, правая шкала ординат, масштаб натуральный). Шкала абсцисс — логарифм числа попыток для достижения N ₂ = 10. Получено компьютерным моделированием

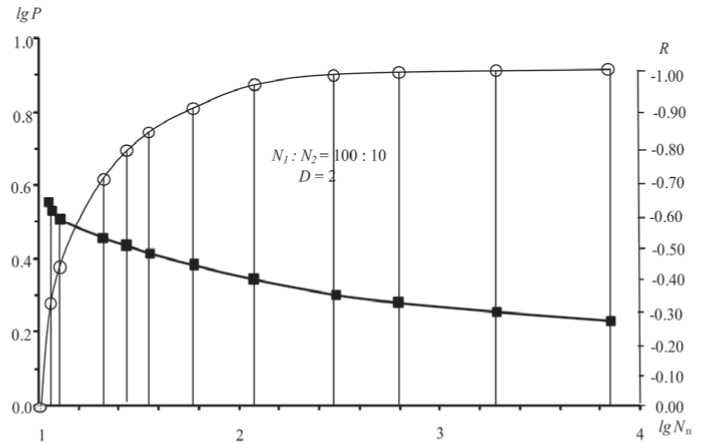
Рис. 7. Номограмма (см. рис. 6) при критических значениях Р_кр <  2.98

шагом, тем самым выстраивается кривая зависимости N 2 — N _п при заданном P _кр. Затем по известному значению P_N1n₂ (и, соответственно, R ) находят по номограмме требуемое для получения ^^ значение P _кр. С этим значением, как с фильтром, многократно моделируются N ₍точек, а затем поштучно N ₂ точек с фильтром и получают целый ряд модельных значений P_№Af и соответствующих им значений R . По ним строят гистограмму, по которой находят границы доверительных интервалов для значения R .

Одна из проблем в исследовании пространственной коррелированности типов точек заключается в правиль ном расчете среднеквадратического отклонения потенциала взаимного влияния типов точек. Очевидно, что использование большего числа точек уменьшит погрешность оценки потенциала. Но без моделирования трудно ответить на вопрос, применима ли здесь зависимость оР =—Д^, в д ^^2 Ж ’ которой оРм ХТ — средняя квадратическая погрешность взаимного потенциала влияния точек первого и второго типов, п^ — средняя квадратическая погрешность взаимного потенциала влияния пары точек. Неясно также, какой результат будет верным, если Мозначает число пар, в которых

ни одна точка не повторяется дважды и более, или возможное число разных пар. Например, пусть N ₍= 2, N 2 = 2. Тогда в первом случае в расчет следует брать две пары: (1,1), (2,2), во втором - четыре: (1, 1), (1, 2), (2, 1), (2, 2). На первом месте указан номер точки первого типа, на втором — второго. Не является ли повторное использование тех же точек в других парах только кажущимся увеличением исходной информации?

На рис. 8 показаны результаты первого этапа компьютерного моделирования, из которого видно, что при одинаковой суммарной численности точек N ₍+ N , наименьшее значение о( P ) получается при равном соотношении типов N ! = N 2 .

Заключение

Заложены основы статистического анализа пространственной коррелированности геологических объектов. Разработаны алгоритмы и компьютерные программы: а) расчета потенциала взаимного влияния совокупностей разнотипных объектов, б) меры их коррелированности, в) моделирования независимого или зависимого их размещения, г) проверки статистических гипотез о параметрах зависимости.

Этот междисциплинарный результат может применяться в минералогии, петрографии, геохимии, рудном деле и обогащении полезных ископаемых. Применение его для количественного анализа металлогеничес-ких, геохимических и прогнозных карт будет способствовать выявлению

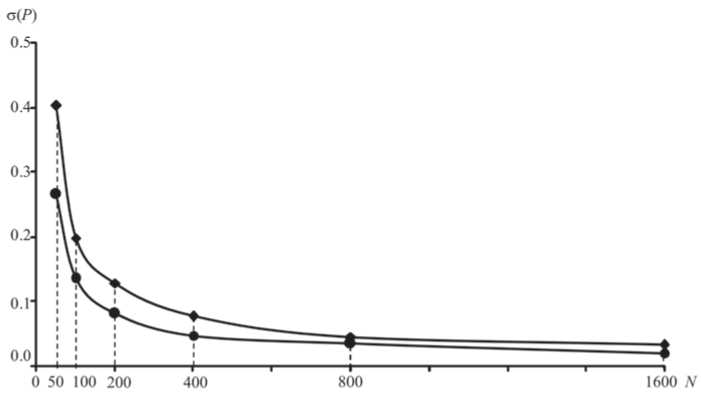
Рис. 8. Кривые зависимости среднего квадратического отклонения о (Р) взаимного потенциала влияния между типами точек и суммарной численностью точек: ромбы — при случайном распределении долей типов точек, кружки — при фиксированных долях 0.5/0.5

скрытых закономерностей в размещении объектов и повышению эффективности поисково-оценочных работ.

Разработка может применяться в биологии, сельском и лесном хозяйстве, в географии и других отраслях, объектами которых являются пространственные данные.

В заключение мы обращаем внимание на то, что введенная мера пространственной коррелированности типов геологических объектов не имеет ничего общего с известным коэффициентом корреляции между признаками (свойствами), характеризующими точки-объекты. Такая корреляция выражается на графиках тяготением точек в случае двух признаков к линии, называемой линией регрессии. При очень хорошей кор реляции точки ложатся так плотно к линии, что признаки становятся функционально связанными. При трех и более признаках точки могут вытягиваться в признаковом пространстве также вдоль линий и поверхностей, например, плоскостей или гиперплоскостей.

Совсем другое дело — пространственная коррелированность типов точек, которая приводит не к анизотропии в их расположении, а к изотропным сгусткам и разрежениям, тяготеющим друг к другу, для разных типов точек при R>0 , или наоборот, когда флуктуации плотности точек разного типа имеют тенденцию к отталкиванию.

Рецензент д. г.-м. н. В. И. Ракин

Первый маршрут. Слева направо: В. Лукин, М. Куртис (Великобритания), Глория Хайльбронн (Франция), И. Котик, В. Матвеев, А. Калмыков. Пай-Хой, р. Хальмер-Ю. Фото П. Мянника (Эстония)