Случайность и пространственная коррелированность разнотипных геологических объектов в пространстве. Часть 1: метод сочетаний типов ближайших точек

Под точечными геологическими объектами, размещению которых в пространстве посвящена статья, понимаются такие, размеры которых малы по сравнению с расстояниями между ними. Таковы месторождения или рудопроявления на геологических картах, зёрна редких (непородообразующих) минералов, рассеянные по площади шлифов или объему образцов. Если обозначить точками центры таких тел или частиц, то их размещение также можно с некоторыми ограничениями анализировать сходными методами.

Под точечными объектами могут пониматься не только физические частицы и тела в физическом пространстве, но и точки, изображающие на графиках состав и другие свойства горных пород и минералов.

Это расширяет проблему статистического анализа размещения точек на многомерные случаи.

Отметим, что эта проблема имеет междисциплинарный характер и важна как для Вселенной в целом с её обширной иерархией космических тел, так и для отдельных отраслей науки: экологии, биологии, химии, материаловедения, географии, ландшафтоведения, геоморфологии и морфометрии, а также для экономических и социальных наук. В её рамках группируются задачи по установлению случайного распределения точек или статистическому доказательству их тенденции к регуляризации или группировке (кластеризации), тяготению к определенным контурам распространения горных пород или других объектов, а для то чек разных типов — к их «тяготению» или «отталкиванию» друг от друга. В настоящее время эти вопросы остаются в математической статистике наименее изученными, так что анализ металлогенических и прогнозных карт проводится «на глазок», без количественной проверки статистических гипотез.

Под случайным размещением (расположением) точек понимается такое, при котором координаты какой-либо точки не зависят от координат всех других точек, а также каждая компонента координаты точки (переменная) не зависит от других компонент той же точки. Таким образом, при случайном размещении каждая компонента координаты имеет прямоугольную функцию плотности вероятности и контроли-

руется попаданием внутрь контура возможного размещения точек. Каж дая точка в этом случае имеет равную вероятность оказаться в любой области исследуемого пространства. Статистический анализ таких размещений традиционно ведется с помощью распределения Пуассона. Простран ство подразделяется на равные ортогональные ячейки (строго говоря, не обязательно равные и не обязатель но ортогональные, но отказ от этого лишь усложнил бы вычислительную реализацию анализа). Число ячеек l рекомендуется выбирать равным числу точек N. Составляется гистограмма числа ячеек, содержащих n точек (n = Q^m, где m — максимальное наблюдаемое число точек в одной ячейке, m < N).

Вывод о случайности размещения делается по результатам расчета критерия хи-квадрат х2:

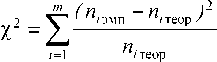
где n_{i эмп} — наблюдаемое (эмпирическое) число ячеек, содержащих i точек, ni _теор — теоретическое число ячеек, содержащих i точек, вычисленное при условии случайного размещения точек в исследуемой области, при числе степеней свободы f= m — 2 . Теоретические (пуассоновские) частоты ni _теор вычисляются по формуле:

X^z е"^х n.^PCi)-^——! , г!

где P(i) — вероятность появления в ячейке i точек, X — среднее число точек на ячейку (рекомендуется, чтобы X было близко к 1).

По рекомендациям профессиональных статистиков, в выражении (1) суммироваться должны слагаемые, в которых ni теор больше 3, а некоторые утверждают даже, чтобы оно было больше 5 [4, стр. 243]. Чтобы удовлетворить этому условию, приходится объединять соседние интервалы гистограммы частот, что уменьшает число степеней свободы и снижает надежность выводов. Особенность пуассоновского распределения такова, что вероятность появления ячеек с большим (4 и более) количеством точек при Х~1 сильно уменьшается, так что даже при большом числе ячеек (и, соответственно, точек) приходится довольствоваться критерием х2 при очень малом числе (1, 2, 3) степеней свободы. Причина снижения надежности выводов заключается в том, что распределение суммы (1) отклоняется при малом числе степеней свободы от теоретического табулированного распределения хи-квадрат.

Второй недостаток критерия х² вызван тем, что распределение х² является непрерывным, а величина, рассчитываемая в качестве критерия согласия по формуле (1), имеет дискретное распределение: суммируемые в (1) величины суть частные от деления целых величин на целые. Когда величины ni _эмп и ni _теор велики, частное от их деления мало отличается от частного при делении непрерывных величин. Но в случае распределения Пуассона эти величины очень малы и распределение х² становится «сильно дискретным» и отличающимся от табулированного в статистических таблицах критических значений. Поэтому для необходимого числа точек и ячеек возникает потребность многократно моделировать распределение точек по ячейкам в соответствии с законом Пуассона и использовать эти результаты непосредственно для проверки гипотезы о случайности размещения точек в пространстве.

Нулевая гипотеза заключается в том, что изучаемое распределение точек по ячейкам пространства — пуассоновское. Альтернативой по умолчанию принимается гипотеза, что существует какое-либо другое распределение, принимаемое за «закономерное». Если нулевая гипотеза отклоняется, требуется провести дальнейший анализ: в какую сторону от случайного отклоняется анализируемое распределение: в сторону ли скученности точек, разделенных изреженными областями, или в сторону их более равномерного, чем по Пуассону, размещения. В первом случае частоты ячеек с нулем точек и с большим количеством точек будут выше пуассоновских, а с числом точек, близким к среднему — ниже. Во втором случае число ячеек с числом точек, близким к 1, будет больше пуассоновских.

Тема анализа размещения точек одного типа этим далеко не исчерпана. Нами составлен комплекс из 19 программ, включающий моделирование точек в пространствах размерностью до 20, от почти регулярного до сильно кластеризованного, их визуализацию на экране, расчет основных статистик размещения, моделирование устойчивости этих статис тик, диагностику кластеров, поиск ближайших и взаимно ближайших точек и другое. Некоторые из этих результатов опубликованы [3]. Теперь мы рассмотрим два отличающихся по смыслу типа точек. Действительно, геологу зачастую более важно выяснить, зависит ли размещение месторождений (пусть это будет первый тип точек) от размещения геохимических аномалий или иных геологических тел (другой тип точек), для того чтобы использовать эти данные в качестве поисковых признаков, чем думать о случайности размещения по отдельности точек каждого типа.

Прежде всего анализу размещения необходимо подвергнуть отдельно каждый тип точек (для определенности — белых и черных), а затем уже проверять гипотезу о случайности размещения белых точек по отношению к черным .

Визуально на плоскости положительная корреляция выразится в том, что ближайшими к белым будут наблюдаться преимущественно черные точки, и наоборот. При отрицательной корреляции белые точки будут тяготеть к белым, а черные к черным, а при отсутствии корреляции никакого предпочтения не окажется. Задача заключается в том, чтобы установить отсутствие или наличие корреляции и её знак. Для решения задачи можно предложить несколько вариантов, прежде всего зависящих от состава исходных данных.

Рассмотрим метод, в котором исходные данные представляют собой координаты точек. Тогда проверку гипотезы о независимости распределения белых точек по отношению к черным можно провести методом сочетаний типов ближайших точек.

В этом методе по координатам точек рассчитываются расстояния между каждой точкой и остальными. Затем выбираются расстояния между ближайшими точками, отмечаются их типы: бб, бч, чч и подсчитывается число отмеченных сочетаний типов N бб , N _5ч, N _чч. Здесь следует заметить, что каждая i -тая точка в общем случае может встретиться в сочетаниях дважды: в качестве ближайшей к j -той и в качестве той, к которой ближайшая k -тая (j ^ k ) . И только когда j=k , эти точки ( i -тая и j -тая) будут взаимно ближайшими и их сочетание встретится один раз. При подсчете числа сочетаний каждого типа следует учитывать это обстоя-

тельство. При положительной корреляции между типами б и ч среди сочетаний будут преобладать бч, при отрицательной — бб и чч, при отсутствии корреляции их соотношение будет таким, какое мы получили бы, моделируя независимые распределения Nб белых точек и Nч черных. Многократно моделируя такие рас пределения, мы установили удивительный, но при внимательном рассмотрении оказавшийся естественным факт, что при независимом случайном распределении точек доли пар бб, бч и чч среди ближайших то чек всегда равны и определяются числом черных и числом белых точек, а именно эта доля d равна:

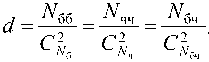
где С—ч — число сочетаний из Nб бе лых точек по две,

' - ₂ , ⁽³⁾ С^ — число сочетаний из N _ч черных точек по две,

2       ’

/^2

— число сочетаний по две точки разного цвета — из Nб белых и Nч черных,

.

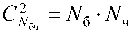
Результаты 500-кратного моделирования случайного размещения N б белых точек и независимого от него N _ч черных точек представлены в таблице. В ней для каждого сочетания численностей N б и N _ч в верхней строке указаны теоретические по формулам (3) — (5) числа сочетаний, в средней строке — эмпирическое среднее из 500 моделирований, в нижней строке — отношение эмпирического числа к теоретическому, т. е. величина d .

К сожалению, постоянство средних значений d для каждого варианта соотношения численностей Nб и Nч и плавный ход увеличения d при увеличении числа точек (рис. 1) не избавляет нас от необходимости многократно моделировать ситуацию с независимым случайным распределением Nб и Nч точек, так как для проверки гипотезы об отсутствии пространственной коррелиро-ванности необходимы не только оценки математических ожиданий d, но и закон распределения указанных долей. Результаты многократного (500 повторов) моделирования независимого случайного распределения 25 белых и 25 черных точек дало следующие результаты: d = 0.041, Sd = 0.0087, A = 0.078, E = -0.073 для среднего, среднего квадратического отклонения, асимметрии и эксцесса соответственно. Получена гистограмма величины d (рис. 2). Она является основой для проверки гипотезы о независимости распределения белых и черных точек. Для этого гистограмма сглаживается, выбирается уровень значимости (здесь он выбран 10 %) и с обеих сторон на модельной кривой плотности вероятности отсекаются области с площадью под кривой по 5 %. Могут быть случаи, когда по причинам содержательного характера положительная (или отрицательная) корреляция между точками невозможна. Тогда на кривой плотности распределения критерия dследует отсечь не по 5 % площади с обоих концов, а 10 % со стороны, в которую значение критерия может изменяться при наличии положительной (отрицательной) корреляции.

В нашем случае нижнее критическое значение d равно 0.0245, верхнее — 0.0525. Фактическое значение d составило 0.041. Таким образом, значение критерия находится в интервале допустимых для независимого распределения значений. Этого и следовало ожидать, так как анализировалась совокупность точек, смоделированная при условии независимости распределения черных точек от белых.

Недостатком разработанного метода сочетаний типов ближайших

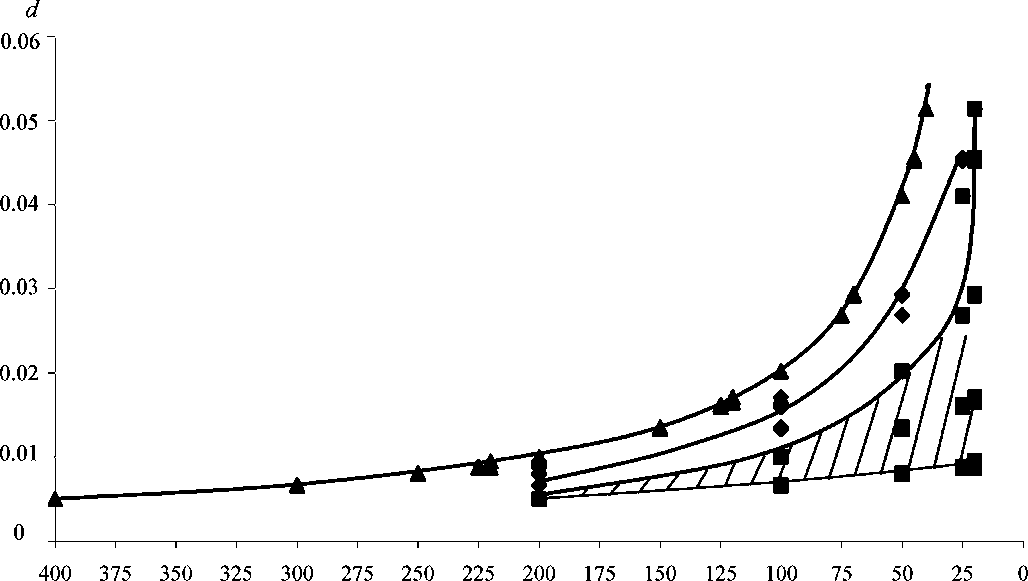
Рис. 1. Изменение средней доли сочетаний типов бб, чб и чч среди ближайших точек в зависимости от количества точек преобладающего типа (ромбы), второстепенного типа (квадраты) и суммы точек обоих типов (треугольники). По оси абсцисс — количество точек (по данным табл.). Заштрихована область расположения кривых с малым числом точек второстепенного типа

Число сочетаний точек типа бб, чб, чч

Число белых точек X	Среди какого множества точек	Число черных точек Уч
		200			100				50			25			20
		бб	чб	ЧЧ	бб	чб		чч	бб	чб	чч	бб	чб	чч	бб	чб	чч
200	среди всех	19900	40000	19900	19900	20000		4950	19900	10000	1225	19900	5000	300	19900	4000	190
	среди ближ.	99.5	200.0	99.5	133.3	132.0		34.6	159.2	81.0	9.3	177.1	44.5	2.7	181.1	36.8	1.5
	их доля d	0.005	0.005	0.005	0.0067	0.0066		0.0070	0.0080	0.0081	0.0076	0.0089	0.0089	0.0091	0.0091	0.0092	0.0078
100	среди всех				4950	10000		4950	4950	5000	1225	4950	2500	300	4950	2000	190
	среди ближ.				49.5	100.0		50.5	66.8	66.0	17.1	79.7	40.2	4.9	82.7	34.2	2.9
	их доля d				0.0100	0.0100		0.0102	0.0135	0.0132	0.0140	0.0161	0.0161	0.0163	0.0167	0.0171	0.0156
50	среди всех	расшифровка чисел _____ в ячейках таблицы ___________							1225	2500	1225	1225	1225	300	1225	1000	190
	среди ближ.		200						24.6	50.5	25.0	32.7	34.5	7.8	35.3	28.9	5.8
			X. =19900	(Д = 40000	Хч =19900
	их доля d								0.0201	0.0202	0.0204	0.0267	0.0276	0.0261	0.0288	0.0289	0.0306
25	среди всех		Хб=99.5	N46 = 200.0	N44 =99.5							300	625	300	300	500	190
	среди ближ.		d№ =0.005	d46 =0.005	d_ = 0.005							12.6	25.1	12.4	13.7	22.9	8.3
	их доля d											0.0419	0.0401	0.0412	0.0457	0.0459	0.0439
20	среди всех														190	400	190
	среди ближ.														9.8	20.4	9.7
	их доля d														0.0519	0.0511	0.0512

Примечание. Верхняя строка — расчетное среди множества всех точек по формулам комбинаторики, средняя строка — эмпирическое среднее среди совокупности ближайших точек при случайном независимом их размещении в 500 моделях; нижняя строка — доля этих сочетаний d

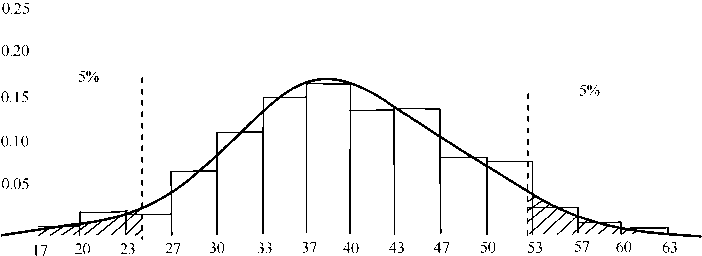
Рис. 2. Гистограмма и кривая плотности распределения доли сочетаний точек типа бб по данным моделирования независимого случайного размещения 25 точек б и 25 точек ч . На оси абсцисс — доля сочетаний типа бб , умноженная на 10³ с округлением. На оси ординат — частости. Заштрихованы критические области критерия для уровня значимости 10 %

точек является использование информации о расположении только ближайших точек, тогда как пространственную корреляцию (или её отсутствие) создают все точки обоих типов. В части 2 будет изложен метод потенциала взаимного влияния, обладающий свойством достаточности, в котором при расчете критерия ис- пользуется вся информация о расположении точек. В нем предусмотрено моделирование совокупности точек с заданной пространственной корреляцией их типов, а также анализ содержательных примеров из области геологии и минералогии. Предполагается также анализ мощности предложенных критериев ме тодами компьютерного моделирования.