Small towns in the spatial structure of regional population distribution

Автор: Makarova Mariya Nikitichna

Журнал: Economic and Social Changes: Facts, Trends, Forecast @volnc-esc-en

Статья в выпуске: 2 (50) т.10, 2017 года.

Бесплатный доступ

The article discusses the role of small towns in the spatial structure of the regional population. The purpose for the study is to assess the irregularity of spatial distribution of urban population in the Sverdlovsk Oblast and substantiate the prospects for regional distribution system dynamics by using the methods of mathematical modeling. The author analyzes various domestic and foreign theoretical and methodological approaches to analyzing spatial disparities in deployment of economic potential and human capital throughout regions and countries. The author's approach is to apply the methodological tools of Zipf's law, which proved its effectiveness during the study of urban population dynamics in the works of both foreign and domestic scholars, to study trends and prospects for demographic development in the Sverdlovsk Oblast. The research has helped reveal actual and ideal Zipf's distribution for towns of the Sverdlovsk Oblast during 1989-2015. Based on the methodology the author calculates the values of optimal population in the towns of the Sverdlovsk Oblast in each period and concludes that over the past 25 years the deviation of actual distribution from Zipf's distribution has decreased...

Еще

Small towns, population, spatial distribution, zipf's law, socio-demographic development, development disparities, sverdlovsk oblast

Короткий адрес: https://sciup.org/147223923

IDR: 147223923 | DOI: 10.15838/esc.2017.2.50.10

Текст научной статьи Small towns in the spatial structure of regional population distribution

The development of the distribution system and active urbanization processes in the world have led to the formation of both large and small settlements of the urban type. Nowadays small and medium-sized towns play a significant role in the social development, being the custodians of the cultural heritage and national coloring of the country. In Russia, small towns include settlements with a population of 10,000-50,000 people with non-agricultural specialization of the economy (industry, trade, service industries). Small towns make up about 2/3 of all cities in the country, and the population in them totals 16,600,000 people accounting for 16% of the urban population of the country. In addition to it, 38,200,000 people of the rural population are also in the area of influence of small towns, because most small towns being the centers of municipalities take on the role of socio-cultural centers as well [2]. Thus, the socio-economic situation of small towns largely determines the development level of the country in general (especially its Siberian and Far Eastern parts) and the social and economic well-being of its citizens.

Most of small towns were formed as administrative, socio-cultural or manufacturing centers and have remained that way till this very day. At the same time, despite their central role in the binding of economic space of Russia, imbalances in the development of small and medium-sized towns on the one hand and large cities on the other hand have been increasing. These imbalances are associated not only with differences in the economic capacity of cities of different types, but also with the contradictions of demographic development. While the population of large cities is considerably increasing, the population of small and medium-sized towns is declining rapidly. The following common reasons for such dynamics have been noted: objective sociodemographic and economic processes, as well as agglomeration processes that contribute to the population shift to large, more developed and attractive cities, which possess a well-developed amenity infrastructure and provide wider opportunities for labor and social realization of an individual [6, p. 15; 9, p. 1516; 1]. However, we believe that the reasons here are somewhat deeper. In this regard, the aim of the study is to represent the model of the spatial distribution of the population in the region, including an assessment of its unevenness, the definition of the role of small towns in the spatial structure of the population distribution, and substantiation of further population changes in small towns.

The study of the spatial distribution of the population and its certain groups was conducted by both foreign and domestic researchers. Thus, U. Isard proposes to assess the evenness/unevenness of the population distribution, calculating the coefficient of localization, which reflects the relative degree of concentration of a certain group of the population in comparison with any other parameter of the national economy. It provides the possibility of comparing the percentage distribution of the two parameters regional profile. The value of the coefficient can range from 0 to 1. For example, if the distribution of a given population group exactly coincides with the distribution of the base value, then the coefficient will be equal to 0; if the entire population is concentrated in one (small) area, then the ratio will be close to 1 [3, p. 212-213].

Other localization coefficients are the coefficients of geographic association, concentration of population, redistribution, as well as indices of dissimilarity, segregation and centralization, their descriptions are provided by U. Izard as exemplified by American studies (Tab. 1).

In national studies, the issue of spatial distribution of the population is investigated, for example, in the context of agglomeration processes. As defined by Yu.S. Selyaeva, agglomeration is a complex, spatially localized, dynamically developing socio-

Table 1. Types of coefficients of localization

Name of coefficient Author Distributions compared Coefficient of geographic association P.S. Florence Shares of manufacturing employment by states: industry i versus industry j Coefficient of concentration of population E.M. Hoover Shares by states: population versus area Coefficient of redistribution E.M. Hoover, P.S. Florence Shares of population or employment in selected manufacturing industries: year b versus year a Coefficient of deviation E.M. Hoover Shares of population by states: white versus Negro Coefficient of urbanization E.M. Hoover Shares by cities: employment in individual industry versus total population Index of dissimilarity O.D. Duncan Shares of workers by areas: occupation group А versus occupation group В Index of segregation O.D. Duncan Shares of workers by areas: specific occupation group versus all other occupation groups Index of centralization O.D. Duncan Shares by census tracts: specific occupation group versus all occupation groups (alternatively, employment in a given industry versus all industry) Cit. ex.: [3, p. 217-218]. system. Its formation assumes regularity in the distribution of cities and providing positive outcomes not only by attracting investments in the development of urban economy as integral economic system, increase in tax capacity and increase in efficiency of budgetary expenditures, but also through quantitative and qualitative enlargement of the regional markets [8], arising as a result of concentration of the population within the territory of agglomeration.

A key criterion for determining the presence and depth of the agglomeration process is the ratio of the population in the structural elements of agglomeration, for example:

– the coefficient of development of agglomeration proposed by P. M. Polyan [5] depends on the size of the urban population of the agglomeration, the number of cities and urban-type settlements and their share in the total population of the agglomeration;

– index of agglomeration developed by Central Research and Design Institute for Urban Development of the Russian Academy of Architecture and Building Sciences represents the ratio of urban population in the external zone to the urban population of the whole agglomeration [5].

However, this approach is limited only by the territory of the agglomeration, and does not allow one to study the spatial distribution of the population in the region in general. In our view, an effective tool to accomplish this task is Zipf’s law, which is an empirical demonstrates high stability. According to the law, the size of a city is inversely proportional to its rank. The law was first discovered to describe the distribution in ranking of cities by the German physicist Felix Auerbach in his work “The Law of population concentration” in 1913 and it was named after the American linguist George Zipf, who in 1949 promoted this regularity, proposing to use it for the first time to describe the distribution of economic power and social status [20, p. 484-490].

N. Moura and M. Ribeiro define Zipf’s law as demonstration of complex systems dynamics: “Demographic distribution of individuals over the earth’s surface having sharp peaks of population concentration in cities alternating with relatively large spreads where population density is much lower, follows power law of typical dynamics of complex system” [18]. The use of this tool is quite a popular method of foreign urban studies and their results confirm the validity of Zipf’s law for different countries [11, 13, 19].

The study of urban settlement in the Russian Federation in accordance with Zipf’s law [10] showed that:

– most small towns and medium-sized cities in Russia lie above the ideal Zipf curve, therefore the expected trend is the continued population decline due to migration to large cities;

– 7 cities with population exceeding one million people (Moscow, Saint Petersburg, Novosibirsk, Yekaterinburg, Nizhny Novgorod,

Kazan, Samara), which are below the ideal Zipf curve, have a significant reserve for the population growth and expect population growth due to the migration inflow, thus allowing them to compensate for the natural decline in their population;

– there are risks of depopulation of the first city in rank (Moscow), since the second largest city (St. Petersburg) and the subsequent major cities are lagging behind the ideal Zipf curve due to the labor demand decrease and increase in costs of living, including chiefly purchasing and renting housing.

Studying implementation of Zipf’s law in the cities of Russia, S.N. Rastvortseva and I.V. Manaeva come to the conclusion that, in general, this law covers small towns (8,60015,300 people) and large cities (66,700 – 331,000 people). In the sampling of cities with population exceeding 100,000 people, Zipf’s law does not cover cities over 1,000,000 people (except for Saint Petersburg) [7].

Our scientific work gives a model of the spatial distribution of the population in the Sverdlovsk Oblast and determines the role of small towns in the system of settlement of this area. The relevance of this issue is confirmed by the approved Strategy of socio-economic development of the Sverdlovsk Oblast up to 2030 (Law of the Sverdlovsk Oblast of December 15, 2015), according to which one of the main tasks is the balanced development of municipal settlements (that are formed mostly around small towns) located on the territory of the Sverdlovsk Oblast, including a decrease of differentiation in the of life in municipal settlements located on the territory of the Sverdlovsk Oblast, the strengthening of intra-regional connectivity of the territory of Sverdlovsk Oblast, promotion of effective interaction between the centers of the emerging agglomerations (municipal formation “The City of Yekaterinburg”, the city of Nizhny Tagil, Serov urban district) and adjacent municipal settlements, the development of an integrated polycentric planning and socio-economic system. The possibility of solving these problems is determined, among other things, by demographic processes occurring throughout the territories of the oblast, since it is they who largely determine the quality of life of the population, on the one hand, and the spatial structure of the region (connectivity, agglomeration of territories), on the other hand.

The application of Zipf’s law for analyzing population dynamics in the cities of the Sverdlovsk Oblast will allow one to consider the prospects for the transformation of the regional settling system and to provide strategic directions on socio-economic and spatial policy, particularly concerning the issues of maintenance and improvement of unique capacities of small towns in the Sverdlovsk Oblast.

Data and methods

Data. The studies are based on the data about the population base of cities and urban-type settlements in the Sverdlovsk Oblast ng to the results of population censuses carried out in 1989, 2002, 2010 and the estimated population as at 1 January 20151.

The sample included 73 settlements, among which in 2015:

• over 1,000,000 people – 1 city (Yekaterinburg);
• from 250,000 to 1,000,000 people – 1 city (Nizhny Tagil);
• from 100,000 to 250,000 people – 2 cities (Kamensk-Uralsky, Pervouralsk);
• from 50,000 to 100,000 people – 8 cities;
• from 10,000 to 50,000 people – 33 settlements (including 3 urban-type settlements);
• less than 10,000 people – 28 settlements (including 5 cities).

Methods. Zipf’s law is a statistical regularity of the size distribution of cities in a country and is well approximated by a Pareto distribution. The meaningful treatment of the law is the following: the probability that the city size is larger than S is proportional to 1/S and the proportionality factor is equal to β . If β = -1, then the largest city is twice as big as the second largest one, and three times as big as the third largest city, and so on. As a result, in regression:

ln(Si) = α + β ln(Ri) + εi , where ln(Si) is the logarithm of the population of the i-th city, and ln(Ri) is the logarithm of the counting number of the i-th city in the descending sequence, the coefficient β is equal to -1 [4].

Thus, cities below the ideal Zipf curve are characterized by a shortage of population, and those located above it are the cities with surplus population. The regressions were used to calculate the “ideal” population size and estimate its surplus/shortage in a particular city.

Results and discussion

According to the territorial body of the Federal State Statistics Service in the Sverdlovsk Oblast, from 1989 until 2015 the total urban population in the region has been reduced from 40,113,000 to 36,489,000 (by 9 p.p.). The population decline was noted in all urban-type settlements of the Sverdlovsk Oblast, with the exception of the cities of the emerging agglomeration “Big Yekaterinburg”: Yekaterinburg, Verkhnyaya Pyshma, Sredneuralsk, Aramil, which have the population increase by an average 14 p.p. Due to the redistribution of the urban population in the region, the number of towns with population less than 10,000 people has increased from 18 to 28, the number of small towns with a population of 10,00050,000 people has reduced from 39 to 33 and the number of medium and large cities with population over 50,000 people has also decreased from 16 to 12. And the flow of the population, as it had been noted above, was carried out mainly to Yekaterinburg and its satellite cities, as well as outside the Sverdlovsk Oblast.

Figure 1. The Zipf distribution for cities and urban-type settlements in the Sverdlovsk Oblast as of January 12, 1989

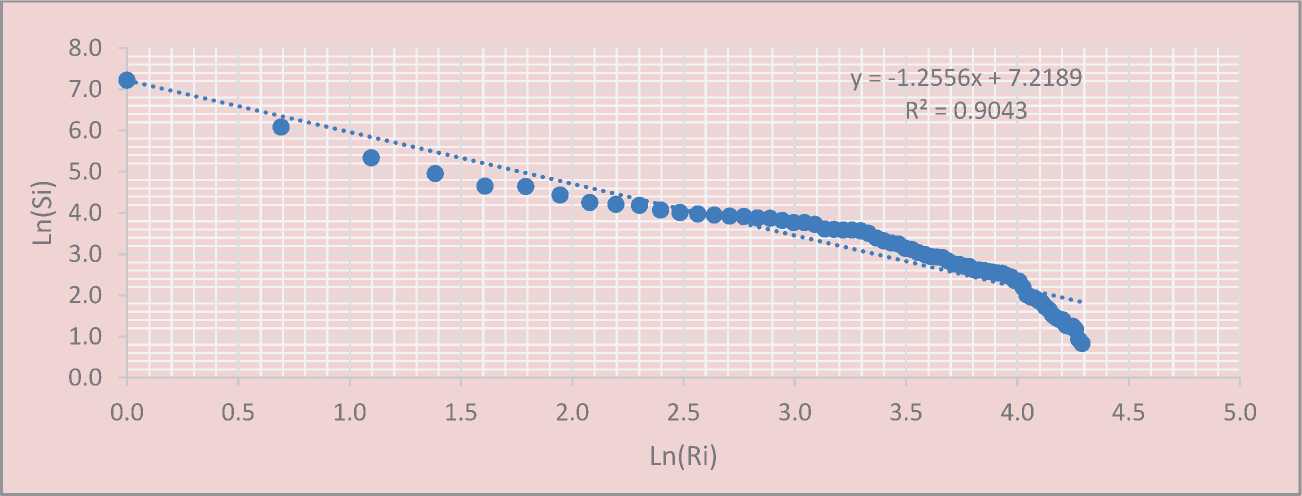
Source: City population. Population Statistics for Countries, Administrative Areas, Cities and Agglomerations – Interactive Maps and Charts. Available at: (accessed 26.05.16)

Figure 2. The Zipf distribution for cities and urban-type settlements in the Sverdlovsk Oblast as of October 9, 2002

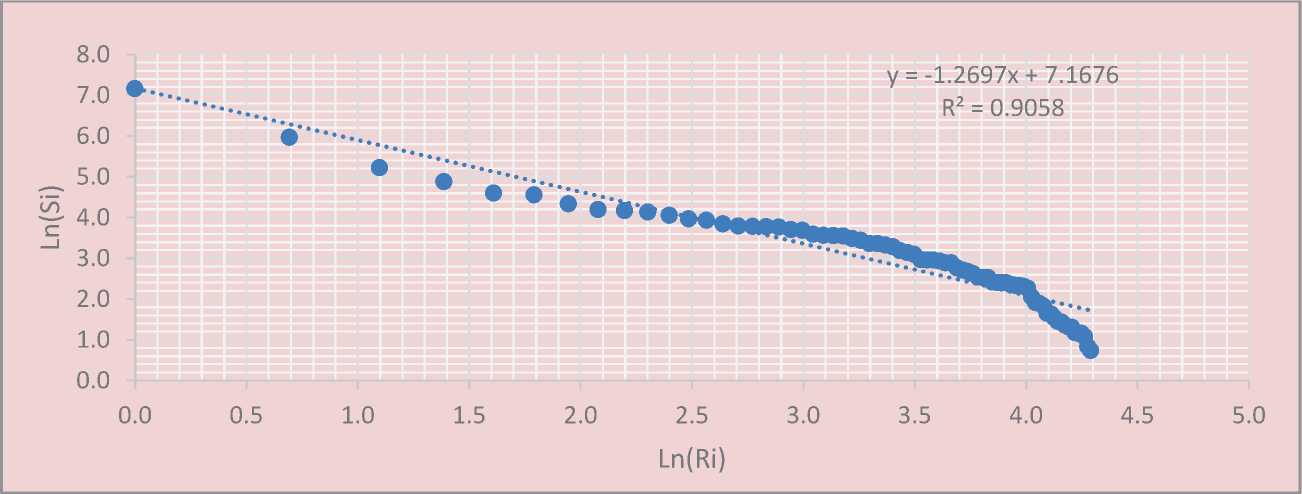
Source: City population. Population Statistics for Countries, Administrative Areas, Cities and Agglomerations – Interactive Maps and Charts. Available at: (accessed 26.05.16).

According to the data on the population in cities and urban-type settlements of the Sverdlovsk Oblast, the Zipf distribution over four periods (Fig. 1–4) was constructed. The regressions indicated in these figures make it possible to calculate the population optimum for each of the settlements included in the study and to quantify the surplus or shortage of the population in various years (Tab. 2). It should be noted that the years 2010 and 2015

Table 2. Actual population and population optimum in the cities and urban-type settlements in the Sverdlovsk Oblast, thousand people

CD OU

⁰⁰cy —

О ZD из

cd LO

LO CO

LO co

CD CO

co cxi

CD to

CD eu

Cxj

CD cd

to cd

CD LO

cxi

CXJ CD

CD cd

CD OD

to CD

to cd

to CD

to cd

° E 1 E Я

LO to

LO CD

cxi

CD cd LO

LO cxj

to cxi CD

CD to

LO CD

CD У

04 cxj

CD cd co

LO co

to cxi co

CD co

LO cd cxj

CD CXJ

LTD CXJ

CD cd ou

co cxi ou

cxi

CD OU

CD CD

LO cd

CD У

LO cd

cz> co

LO cxi

СУ ^

< ।

CD cd OU

co LO co

LO CXJ

о cd CD

CD cxi co

CD CD

LO CD

cxj co

OU cxj CD

CD od LO

CD LO

OQ oS

CD CD

OD co

cxi

CXJ

C*D

OD ou

CD OU

co cd ou

cd ou

CD cxj ou

CD OU

CD ou

03 -#—।

-CZ cz ' оз

о E

E ~ co

"c/5

CZ CD E 05

i/5 2

□_

OD co

i/5 05

ZD о > о

03 -O

CX5

"о

о о

03 DC

о CZ 00 £5 5

CD 03

'o CZ GO CD —1

CO CZ 05

-CI

05 ^

co E

о CZ co СУ 5

03 05

—I

"o uzz

OS “O

E OD

о c -S o’ to

05 >

co 1X1

> о

-C

E 05 ^

CZ 05

> 03

СУ

О CZ co cy 5

8 ZD 03

TD 03

■e 03 GO

-C

■O 05

05 > О

CO 05

-C

"g/5

CD OU

■e CZL о = to ⁰⁰

CXJ cd

cxi

LO CO

CD OD

eu cd co

co cd to

°q LO 04

cxi

CD cd

03 LO

CXJ OD

OD OD

to CD

LO CD

to OD

OD OD

У OD

° E 1g a®

cd OD CXJ

cxi co

cd cxj OU

о cd CD

CO cd co

OD о

Cxi CD

OD CD

LO LO

OD OD

od co

LO co

CD cd co

CD co

OD cd cxi

CXJ

LO OU

OD cxj OU

to cxi

OD CO

OD LO

СУ "U= D СУ s§ CL

LTD cd CD CXJ

CD CD

cxi cd co

co cxj co

OD OD

LO OD

CD CD

OU CD

CD od LO

CXJ cd LO

CXJ

CD cd

co cd

OD CO

CD to

LO to

OD ou co

OD to

OD od OU

CD CXJ

OU cd CXJ

OU cxj to

CD OD

to OD

CD -cz cz ^4—' CD "о E

ZD c

"c/5

03 E 05

^c/5 05

OD to

СУ

о ^

GO 03

О CL

СЛ ^

> 03 DC

CO E -CZ co

CX5

CZ -CZ

"o CZ 03 03 —1

05 ^ OS CD

CZ -CZ

о m

05 CZ 05

О 05 ^

03 05

"c/5

co cy ^

05 "О >

-CZ

03 DC

o’ —I

ZD co

05 >

О E OD

03 > 03 co

-CZ о

■О

GO 05 ^

-CZ СЛ

E 05

-c:

▻4

"^ CZ 05

СУ

cy ro

2 □)

CD CZ

"c/5

CD CO OD

g)⁰⁰СУ — t B

co ⁰⁹

CXJ Cxj CO

OD co

OD CXJ

OU OD

о CD

°?

о LO

о cxj

OU cd

cxi

ou cd

¹⁰

cxi

OD OD

CD cd

о cd

to CD

° E 1 E П

LO CO co

co cd

OD CO

CD cd

CD О

CD to

CXJ

CD CD

LTD s

LO ud

CD cxj

OD cd co

CXJ

CD co

eq cd co

OD OU

ou cd ou

CD OU

CXJ

LO 04

co cxi ou

CD ou

OD OD

eq cd

OD cd

to cd

CXJ LO

cz су ^ < 1

cd s co

OD CO

CD cxi

OU cxj У

CD CD

LO CD

LO od LO

CXJ

LO LO

CD LO

co od У

LO У

cd У

CD cd to

CD to

CD cd co

LO to

LO cd co

OD CXJ

CXJ

co cd cxj

LTD CXJ

CXJ co CXJ

LO cxj CXJ

CXJ

OD OD

CZ CD E 03

03 GO

CD -CZ

CD E 05

*05

i/5 s

"c/5

03 E 05

"8 =3 о > ^03

о о

GO 03 -O

СЛ <

GO > 03

о co E 5

cxS "O

> 03 DC

V) 03 ___________1

05 CO

03 >

05 E -CZ 03

CZ -CZ

j O5

03 OS

СУ

-CZ

СУ

СП

CO 05 5

-CZ

GO =5

о E

"CL СУ x^:

05 О

___________1

"o J=

ZD О

03 > 03 co

-CZ о

о CZ 05

CD О

s ZD О

из 05 5

СУ

CZ -CZ о 03

CO 1X1

"E CD

05 (75

co cd

CD cd

LTD

OD CD

co CD

cu cu

cu cd

LO cd

co cu

oo cd

CD CU

о OU

CD CD

co a

CD CD

OD CO

CD cd

OU cd

CD cd

CO CD

CD cd

LO cd

co cd

cu cd

CD cd

co id

CD LO

LO id

co LO

cu id

CD id

Ю cd in co co

'er CO

CM co

a co

CD cd

'er

CO OD

CO CD

CD CD

'er CD

ем

СУ)

'er cd

UD CD

OD LO

CM LO

о LO

CD LO

CO cd

CM cd

CD cd

'eT cd

CM CM

OD cd

co co

"e/D ё cr

co go

"c/5 CO

Ё ra <

ё <

"co co

о CD

"co

cO >

CD CO in

CCS E

ex'

CO -G

CD OO

03 ‘cz -G

CO CD

"co

"c/D

-CZ

CO > GO О co

О UD

>, "cti

03 co

-CZ

"^ ^> 03

О > о

03 03

IE <

JZZ GO

"С CO ^

CCS

a CD

E "as D_

JZZ

о га

Q-

"c/5 ,G "co "co

LO cd

co cd

CD cd

OU cd

CD CD

eq CD

О)

eq cd

LO cd

'З; cu

eq cd

CD CU

LO CU

OD CU

eq cu

eq cd

eq cd co co

OU cd

co cd

a cd

°?

CD CD

co CD

co cd

co od

CM co

о cd

CD cd

co cd

iq co

CM CD

CD cd

OD LO

co LO

CD LO

cd о

CD od

CD cd

CD IO

CO cd

CD OU

CD cd

LO CD

co CD

co о

co CD

CD CD

cu cd

eq id

OD cd

eq cd

CU cd

eq cd

CU cd

OD cu

co cd

co cd о

CD jro

CCS

CCS CO

ГО ГО c

"c/5 .C

Ф DC

"co co

CCS <

ra^

03 ro

"5>

-CZ

"5)

CD OD .03 "c -CZ

co JZZ

oo co

cz jg

-CZ

"co cz co

о >

"c/5 > О

CVS co о CD

E -CZ CZ)

□_

-CZ

"co

-Q О

-CZ

-C

03 (Z)

"E -CZ

□>

.c:

IE о <

03 03 cz

-с:

ZD О

О CD

СЛ ZD

03 G JZZ

E "aS

CO tn

ra CD

"c/5

03 G О

О .G

"c/5 .c "co "co S

'ef

co co

CD cd

OU cd

co cd

OU cd

co cd

CD cd

co cd

CM. CM

ем

co cd

oo cd

OD cd

CD cd

CD CO

CXJ cd

cu cd

co cd

CSD CO

CD CO

'eT

co cd

CD cd

LTD cd

OD CD

CD CD

eq CDD

eq OD

OD cd

LO cd

eq cd

CD cd

'eT

eq cd

CU CD

CD OD

co cd

^ cd

co id

co cd

CD cm"

eq cm"

eq CM

'er CD

OD cd

LO cd

cu cd

CD id

cu id

'er

eq cd

LO cd

CM cd

CO cm"

eq a

OD g

-O

"c/5 CO

"co ,c

Id cc

"cO

CD CD

"c/5 g CO

о .о

CD m

CCS <

CO cz

-G

"5) j CO

"c/5 о

-G

"co

1± 03

-CZ

c75

CO cz

CO E -CZ

CZ "O о

-Q О

ОЭ

СЛ о CO

-CZ

5) о co

To JZZ OD

-C

03 >

о CD

IE <

-О

ZD О

03 03 с

-CZ

GO ZD

О > 03 cz

JZZ

о co co

03 G О

о _G "c

.G "co "co

S °

200°

similar picture of the distribution of

The period of 2010-2015 (Fig. 3–4) is urban population across the territory of the Sverdlovsk Oblast with a certain tendency to increase, for this reason the figures for 2010 are not presented.

As can be seen in Fig. 1 , in 1989 the location of the urban population in the territory of the Sverdlovsk Oblast had significant deviations from the Zipf distribution. For cities with a population of 10,000-50,000 people the average deviation was 24.9%; for cities with a population of over 50,000 people – 30.5%. This is due to the fact that strict regulation of internal migration prevented the free movement of the population and did not allow one to smooth out interterritorial differences in sociodemographic development.

The transition to the market mechanisms in the 1990s was characterized by polarization of socio-demographic development of the cities of the Sverdlovsk Oblast.

As can be seen in Figure 2 , the deviation from Zipf’s law has also increased toward population shortage in large and mediumsized cities (with population over 50,000 people), averaging 32% (or 568,000 people in total), and toward reduction in the surplus population in small towns (10,000-50,000 people), accounting for an average of 24%(or 239,600 in total). At the same time, it should be noted that the movement of the population during this period has resulted in reduction in surplus/ shortage of the population (in 55 settlements), as well as in its increase (in 19 settlements).

characterized by a further decrease in the polarization of socio-demographic development and by the approximation of the population distribution in the cities of the Sverdlovsk Oblast to the Zipf distribution.

However, one should note two facts concerning the spatial distribution of the urban population across the territory of the Sverdlovsk Oblast as at the beginning of 2015. Firstly, a large population increase in Yekaterinburg has led to its big surplus from the point of view of the population distribution in the region. Secondly, towns (with the exception of the satellite cities of Yekaterinburg) are characterized by the reduction of surplus population. However, though this surplus is still quite significant (188,500 people), it can be freely absorbed by the medium and large cities, which are in need of 554,800 people. Thus, it can be concluded that the population movement from small towns to medium and large cities will continue in the near term and make the spatial distribution of the population in the region closer to Zipf’s law.

Our calculations are confirmed by the findings of other researchers [12, 14, 15, 16, 17] about the spatial distribution of the population being a complex system, tending to some balanced condition (the Zipf distribution), and having the ability to return to it after disasters of different nature (including artificial barriers to the free movement of the population).

Figure 3. The Zipf distribution for cities and urban-type settlements in the Sverdlovsk Oblast as of October 14, 2010

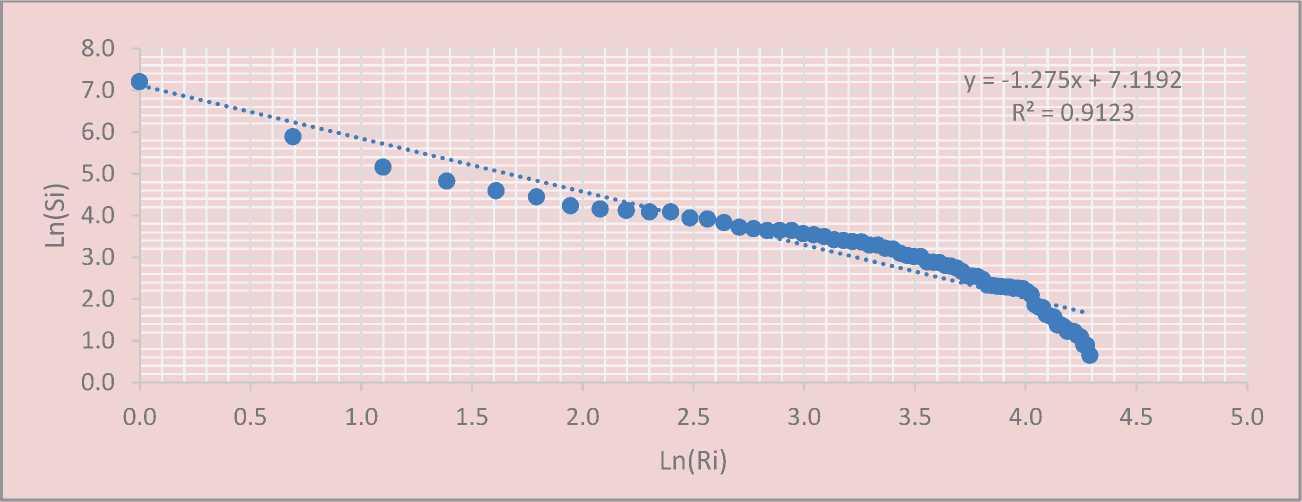
Source: City population. Population Statistics for Countries, Administrative Areas, Cities and Agglomerations – Interactive Maps and Charts. Available at: (accessed 26.05.16).

Figure 4. The Zipf distribution for cities and urban-type settlements in the Sverdlovsk Oblast as of January 1, 2015

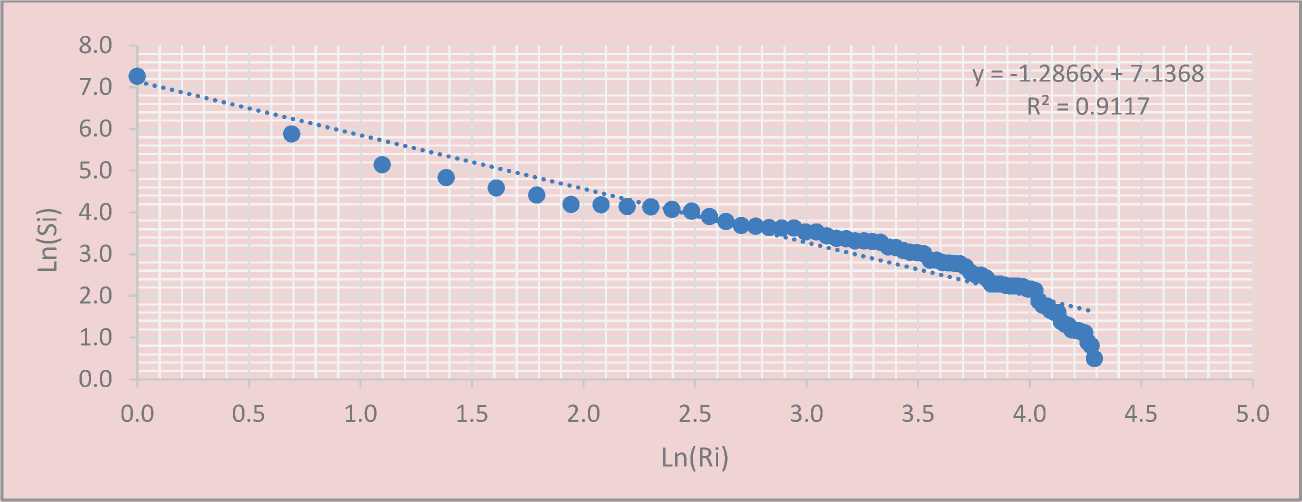
Source: City population. Population Statistics for Countries, Administrative Areas, Cities and Agglomerations – Interactive Maps and Charts. Available at: (accessed 26.05.16).

In comparison with the trend lines indicated in Figures 1–4, the value of the free term and the module of regression coefficient increased during the survey period, which corresponds to the rotation of the trend line in a clockwise direction and its upward movement, and it means the acceleration of the population distribution unevenness and the reduction of the population of small and medium cities. This rresponds to the current nationwide

Zipf’s law, and moreover, in the course of time trend of advanced growth of larger cities, while the share of the population living in cities with smaller population is significantly reducing [10]. Therefore, in the near term small towns will remain the source of human capital for medium and large cities. However, it should be noted that Yekaterinburg has already exhausted the opportunities for increasing its population size. Hence, a well-thought-out policy of the regional authorities is needed to regulate the population migration and to increase the attractiveness of the cities (except Yekaterinburg), which could take the surplus population from small towns.

Conclusion

The spatial structure of the population distribution in the region is a dynamic system that undergoes changes under the influence of demographic and socio-economic factors towards a certain equilibrium state. Numerous foreign and domestic studies have proved that this equilibrium state is determined by Zipf’s law and is revealed in many countries of the world. This allows one to make solid conclusions on the trends, factors and prospects for the development of the settlement systems surveyed.

Our study presents the results of the analysis of the spatial distribution in the cities of the Sverdlovsk Oblast. The data obtained for 1989, 2002, 2010 and 2015 show that in general the distribution of the urban population throughout the region follows the actual distribution gradually shifts towards the ideal Zipf distribution.

It is also determined that large and medium-sized cities are characterized by shortage of the population, and small cities -by its surplus. It should be noted that as a result of the population redistribution in the cities of the region, there is a reduction in the positive or negative deviation of the population of the studied cities from the “optimal” one, i.e. corresponding to Zipf’s law.

Therefore, not only socio-economic factors (imbalances in economic and sociocultural potential) are the reasons for the population decline in small towns and the population growth in large cities, but also the desire of a spatial structure of the population as a dynamic self-organizing system to a more balanced state. In this situation, small and medium-sized cities are donors of human capital for large cities of the region. Moreover, this trend is expected to continue in the near future and it should be taken into account while developing a regional socioeconomic policy as regards the preservation and development of the potential of small towns in the Sverdlovsk Oblast.

In addition, we should emphasize that Yekaterinburg, the largest city of the region, with a population of about 1.5 million people under the existing system of resettlement has already exhausted its opportunities to increase the number of residents without prejudice to the other territories of the Sverdlovsk Oblast.

This fact has to be taken into consideration by regional authorities that should focus on improving the attractiveness of other cities in the region (large and in particular small and medium) in order to stimulate the of area residents and external migrants thus to increase stability and balance of the spatial structure of the population distribution.

Список литературы Small towns in the spatial structure of regional population distribution

Buldakova N.B. Problemy i perspektivy razvitiya malykh gorodov Rossii . Vestnik Shadrinskogo gosudarstvennogo pedagogicheskogo instituta , 2011/1, issue 1, pp. 166-169..
Zykova N.V., Khozyainova S.V. Malye goroda v sisteme sotsial'no-ekonomicheskogo razvitiya regiona: sovremennye tendentsii i problemy . Problemy sovremennoi ekonomiki , 2011, no. 4 (40). Available at: http://www.m-economy.ru/art.php?nArtId=3837 (accessed: 20.09.2016)..
Izard U. Metody regional'nogo analiza: vvedenie v nauku o regionakh . Moscow: Progress, 1966. 660 p..
Kolomak E.A. Razvitie gorodskoi sistemy Rossii: tendentsii i factory . Voprosy ekonomiki , 2014, no. 10, pp. 82-96..
Lappo G., Polyan P., Selivanova T. Aglomeratsii Rossii v XXI veke . Demoskop Weekly , 2010, no. 407-408, pp. 45-52..
Plyusnin Yu.M. Malye goroda Rossii. Sotsial'no-ekonomicheskoe povedenie domokhozyaistv, tsennostnye ustanovki i psikhologicheskoe sostoyanie naseleniya v 1999 g. . Moscow: Moskovskii obshchestvennyi nauchnyi fond, 2000, issue 27. 147 p..
Rastvortseva S.N., Manaeva I.V. Analiz proyavleniya zakona Tsipfa v gorodakh Rossii . Ekonomicheskii analiz: teoriya i praktika , 2015, no. 46(445), pp. 56-66..
Selyaeva Yu.S. Formirovanie gorodskikh aglomeratsii kak instrument dinamichnogo sotsial'no-ekonomicheskogo razvitiya territorii . Inzhenernyi vestnik Dona , 2012, no. 3(21), pp. 765-769..
Vetrov G.Yu. (Ed.). Sotsial'no-ekonomicheskoe razvitie malykh gorodov Rossii . M: Fond «Institut ekonomiki goroda», 2002. 102 p..
Fattakhov R.V., Stroev P.V. Prostranstvennoe razvitie Rossii: vyzovy sovremennosti i formirovanie tochek ekonomicheskogo rosta. Natsional'nyi doklad . Panel'naya diskussiya «Prostranstvennoe razvitie Rossii: vyzovy sovremennosti i formirovanie tochek ekonomicheskogo rosta». 22.06.2015. Finansovyi universitet pri Pravitel'stve RF . Available at: http://fa.ru/projects/forum24/discussion/Pages/Prostranstvennoe-razvitie-Rossii-vyzovy-sovremenno.aspx (data obrashcheniya: 20.09.2016)..
Benguiguia L., Blumenfeld-Lieberthal E. A dynamic model for city size distribution beyond Zipf 's law. Physica A, 2007, no. 384, pp. 613-627.
Brakman S., Garretsen H., Schramm M. The Strategic Bombing of German Towns During World War II and Its Impact on City Growth. Journal of Economic Geography, 2004, volume 4, no. 2, pp. 201-208.
Chen Y., Zhou Y. Multi-fractal measures of city-size distributions based on the three parameter Zipf model. Chaos, Solitons & Fractals, 2004, no. 22, pp. 793-805.
Davis D., Weinstein D. A Search for Multiple Equilibria in Urban Industrial Structure. Journal of Regional Science, 2008, volume 48, no. 1, pp. 29-65.
Davis D., Weinstein D. Bones, Bombs, and Break Points: The Geography of Economic Activity. American Economic Review, 2002, volume 92, no. 5, pp. 1269-1289.
Mansury Y., Gulyaґ L. The emergence of Zipf's Law in a system of towns: An agent based simulation approach. Journal of Economic Dynamics & Control, 2007, no. 31, pp. 2438-2460.
Miguel E., Roland G. The Long-run Impact of Bombing Vietnam. Journal of Development Economics, 2011, volume 96, no. 1, pp. 1-15.
Moura N. J., Ribeiro M. B. Zipf law for Brazilian towns. Physica A, 2006, no. 367, pp. 441-448.
Xu Z., Harriss R. A Spatial and Temporal Autocorrelated Growth Model for City Rank-Size Distribution. Urban Studies, 2010, no. 47 (2), pp. 321-335.
Zipf G.K. Human Behavior and the Principle of Least Effort. Boston: Addison-Wesley Press, 1949. 573 p.

Еще

Статья научная