Смена знака приращения массы при перемещении трех горизонтальных материальных точек по прямолинейным направляющим

В материаловедении при работе с фазовыми диаграммами возникают проблемы, связанные с тем, что участие одной из фаз в трехфазном превращении временно прекращается, а затем возобновляется, но уже с другим знаком приращения массовой доли этой фазы. Например, если приращения масс участников фазовой реакции N → А + В в некотором температурном интервале имеют знаки Δ m A >0, Δ m B >0, Δ m N <0, то при некой температуре Т с эта реакция может принять вид N → А с Δ m B =0, а затем трансформироваться в N + B → A при Δ m B <0. Аналогичные трансформации могут иметь место в различных сочетаниях фаз А , В и N в левой и правой частях реакции. Чаще всего, в дополнение к приведенному примеру, встречается вариант перехода от N → A + B через N → B при Δ m A =0 к N + А → B при Δ m A <0.

При решении этой задачи применительно к каждому конкретному трехфазному превращению необходимо ответить на вопросы:

• 1)    Может ли проявиться в данной фазовой реакции эффект индифферентного поведения одного из ее участников?

• 2)    Если может, то в каких температурных и концентрационных границах?

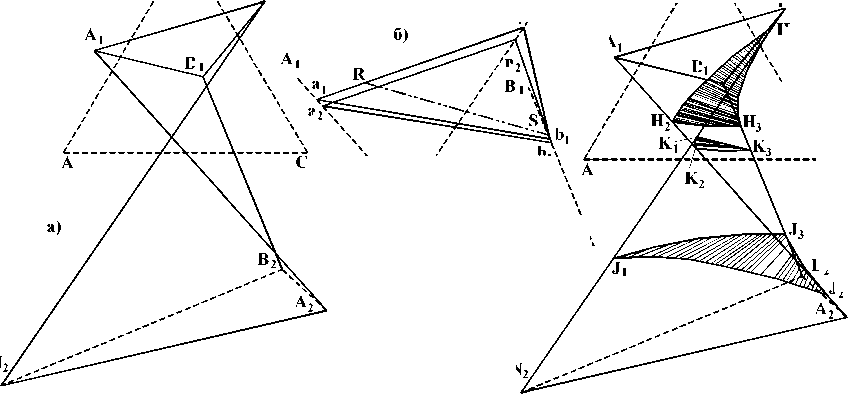
Геометрически задачу можно сформулировать так. Превращение трех фаз происходит в трехфазной области, которую ограничивают три поверхности, задаваемые тремя линиями А1А2, В1В2, N1N2 (рисунок, а). Каждые две из трех линий являются направляющими для линейчатых поверхностей с горизонтальной образующей. Если предположить, что А1А2, В1В2, N1N2 – прямые, то границами области становятся три гиперболических параболоида. Они строятся в смешанной системе координат, которая формируется барицентрическим основа- нием на концентрационном треугольнике АВС (z1, z2, z3), z 1+z2+z3=1, и ортогональной ему осью температур Т (рисунок, е). При любой температуре горизонтальный разрез области представляет собой треугольник (треугольники a 1 b 1 n 1 при Т1 и a2b2n2 при Т2 на рисунке, б).

И эмпирически, и аналитически [1, 2] было доказано, что принятые в отечественной литературе [3-6] методики оценки условий смены типа трехфазной реакции, базирующиеся на исследовании свойств касательной к линии N ₁ N ₂ или к линиям A ₁ A ₂ и В ₁ В ₂, ошибочны. Ошибки проявляются в том, что либо температура смены типа фазового превращения Т с , определяемая этими методами, постоянна [3-5], либо смена знака приращения одной из фаз происходит в температурном интервале, однако определяется он неверно [6].

Применение альтернативных методик - двухвекторного метода Иванова [7] и декартово-аналитического метода Хиллерта-Принса [8, 9] - позволяет оценить температурные границы и очертить концентрационный контур проявления эффекта смены типа трехфазного превращения. Однако метод О.С.Иванова слишком громоздкий и неудобен ни для программирования, ни для использования «вручную». Критерий М.Хиллерта был разработан так, чтобы им можно было пользоваться «вручную», строя серии декартовых систем координат и определяя отклонения вершин треугольников a i b i n i по линейке. Поэтому эти методы не удобны для программирования и не имеют перспектив для применения в четырехкомпонентных и более сложных системах.

Идеи М.Хиллерта, изложенные в барицентрических координатах, позволили создать более совершенный способ расчета границ зануления приращения массовой доли участника фазового превращения [1]. Согласно этой методике, проявление AmB=0 при заданной темпе ратуре Т1 проверялось путем оценки смещения вершин треугольника a2b2n2 при Т2=Т1-dT относительно локальной системы барицентрических координат a 1 b 1 n 1 при Т1. С помощью программы, реализовавшей данный алгоритм, было построено семейство горизонтальных отрез- ков, сформировавших поверхность двухфазной реакции N-^A, на которой AmB=0.

Гораздо более эффективным является алгоритм, описывающий и решающий задачу в глобальной барицентрической системе координат (z 1, z2, z3) треугольника АВС (рисунок). Для центра масс G условия Gеa 1 b 1 n 1 при Т1 и Gеa2b2n2 при Т2 можно записать в виде:

f g1)

^g 2

I g 3 J

f a 11 bn n 11 Y m A1 )

^a 12 ^b 12 ⁿ 12 ^mB 1

v ^a 13 ^b 13 ⁿ 13 JI m N 1 j

fa 21 b 21 n 21 Y mA 2 ' a22 b22 n22  mB2 , va23 b23 n23 JVmN2 j

где ( g 1 , g 2 , g 3 ), ( a 11 , a 12 , a 13 ), ( b 11 , b 12 , b 13 ), ( n 11 , n 12 , n 13 ), ( a 21 , a 22 , a 23 ), ( b 21 , b 22 , b 23 ), ( n 21 , n 22 , n 23 ) - глобальные барицентрические координаты точки G и вершин треугольников при Т ₁ и Т ₂, ( m A 1 , m B 1 , m N 1 ) и ( m A 2 , m B 2 , m N 2 ) - разложение центра масс G на три горизонтальные материальные точки при Т ₁ и Т ₂( m_{A 1}+ m_{B 1}+ m_{N 1}=1, m_{A 2}+ m_{B 2}+ m N =1).

Разрешив уравнения (1) относительно любой пары координат точки G, например, g 1 и g2, можно получить уравнения K1 g 1 + K 2 g 2 + K 3 = 0,

^k1^g 1 ⁺ k 2 ^g 2 ⁺ k 3 = ⁰,                                                    ⁽³⁾

9 1 g 1 + q 2 g 2 + q 3 = ⁰,                                                   ⁽⁴⁾

где K 1 =( b 12 — n 12 )/ 5 1 — ( b 22 - n 22 )/ § 2 , K 2 =( b 21 - n 21 )/ 5 2 — ( b 11 - n 11 )/ 5 1 ,

K 3 =( n 12 b 11 - n 11 b 12 )/ 5 1 +( n 21 b 22 - n 22 b 21 )/ § 2 , 5 1 =( a 11 — n 11 )( b 12 — n 12 ) — ( a 12 — n 12 )( b 11 - n 11 ), § 2 =( a 21 - n 21 )( b 22 - n 22 ) - ( a 22 - n 22 )( b 21 - n 21 );

k1=(a22-n22)/d2-(a12-n12)/d1, k2=(a11-n11)/d1-(a21-n21)/d2, k3=(n 11Я12-n 12a 11)/d 1+(n22a21-n21 a22)/d2, d 1=(a 11-nn)(b 12-n 12)-(a 12-n 12)(b 11-n 11), d2=( a 21 - n 21)( b 22- n 22)-(a 22- n 22)( b 21 - n 21);

q 1=(b22-a22)/D2-(b 12-a 12)/D1, q2=(b 11-a 11)/D1 -(b21-a21)/D2, q 3=( a 11 b 12- a 12 b 11)/D 1+( a 22 b 21- a 21 b 22)/D 2, D 1=( b 11- a n)( n 12- a 12)-( b 12- a 12)( n 11- a 11),

D 2 =( b 21 - a 2i )( n 22 - a 22 ) - b 22 - a 22 )( n 21 - a 21 ).

B

B

C

в)

N 1

N 1

n1

N 1

B 1

n2

B 1

a2

B 2

J

A

H 1

N 2

A2

B 2

B2

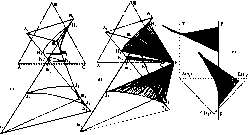
Рисунок. Проекции гиперболических параболоидов, задаваемых направляющими А 1 А2, В 1 В2, N1 N2 (а), схема построения образующего отрезка RS по треугольникам a 1 b 1 n 1 при Т1 и a2b2n2 при Т2=Т1-dT (б), образующие отрезки поверхностей A mA=0, A mB=0, A mN=0 (в), концентрационные границы Н1 Н2 Н;, К 1 К2К3, J1 J2J3 проявления эффектов A mA=0, A mB=0, A mN=0 (г), пересечение проекций образующих отрезков трех поверхностей в точке F (д), поверхности A mA=0, A mB=0, A mN=0 в координатах (z 1, z2, z3, T) (е)

Уравнения (2)-(4) описывают, соответственно, семейства прямых A m A =0, A m_B =0, A m N =0, из которых составляются поверхности двухфазных реакций (рисунок, в, е).

Из анализа уравнения (2) видно, что:

• 1)    При G = n 1 (при температуре T H 1 ) отрезок b 1 n 1 сливается с n 1 n ₂, при G = a 1 этот же отрезок становится параллельным а 1 а ₂ (при температуре T H ₂), а при G = b 1 (при температуре T H ₃) отрезок b 1 n 1 совпадает с b 1 b ₂. Наибольшая ( T H 1 ) и наименьшая ( T H ₃) из трех значений температур задают температурные пределы существования поверхности двухфазной реакции N ^ В . Чтобы их найти, нужно определить точку на пересечении проекций направляющих В 1 В ₂ и N 1 N ₂ (рисунок, г). Подстановка ее концентрационных координат в уравнения В 1 В ₂ и N । N ₂ дает значения T H 1 и T H 3 .

• 2)    При изменении температуры в интервале T H 1 - T H 3 по (2) строятся отрезки RS , концы которых R ∈ a 1 n 1 , S ∈ b 1 n 1 находятся на сторонах треугольников a 1 b 1 n 1 (рисунок, б). Причем продолжения всех отрезков RS пересекаются в одной точке F (рисунок, д). Таким образом, формируемая горизонтальными отрезками RS двухфазная поверхность Δ m A =0 имеет вертикальную направляющую в точке F (рисунок, е).

• 3)    Ранее было показано [11], что если плоскость параллелизма совпадает с координатной плоскостью xOy , то на параллельной ей образующей существует такая точка S , что x - y проекция образующей, принадлежащей второму семейству и проходящей через S , совпадает с x - y проекцией первой образующей. При этом плоскость, построенная на этих двух образующих прямых ортогональна и является касательной к поверхности гиперболического параболоида в точке S . Причем все точки S принадлежат особой кривой гиперболического параболоида, называемой криминантой. Таким образом, все точки S ∈ b 1 n 1 в интервале T H 3 ≤ T ≤ T H 1 принадлежат такой касательной плоскости к поверхности гиперболического параболоида с направляющими B 1 B 2 и N 1 N 2 , что из точек S на плоскости треугольника АВС формируется дискриминантная кривая, а в пространстве - криминанта гиперболического параболоида.

• 4)    В результате, согласно классификации поверхностей [12], двухфазная поверхность Δ m A =0 является прямым коноидом с горизонтальной образующей, который пересекается с гиперболическим параболоидом, образованным направляющими В 1 В 2 и N 1 N 2 по его крими-нанте.

Аналогичный анализ уравнения (3) позволяет определить температурные границы существования двухфазной поверхности N → А при Δ m В =0. Их задают точки К 1 и К 2 (рисунок, в, г), отмеченные на линиях А 1 А 2 и N 1 N 2 при температурах Т К 1 и Т К 2 , которые соответствуют значениям температурных координат точки К на пересечении А 1 А 2 с N 1 N 2 . Отрезки RS тоже пересекаются в одной точке, причем эта точка F – та же самая, в которой пересекаются проекции образующих поверхности Δ m A =0 (рисунок, д). Точки R ∈ a 1 n 1 принадлежат криминанте второго гиперболического параболоида, ограничивающего трехфазную область. Его направляющими служат линии А 1 А 2 с N 1 N 2 (рисунок, г).

Свойства третьей поверхности аналогичны. Проекции ее горизонтальных образующих отрезков тоже пересекаются в точке F , вертикаль в которой является общей направляющей для всех трех поверхностей Δ m А =0, Δ m В =0 и Δ m N =0. Второй направляющей, как и в первых двух случаях, является криминанта гиперболического параболоида, задаваемого направляющими А 1 А 2 и В 1 В 2 .

Таким образом, геометрическая конструкция, которую задает перемещение горизонтальных отрезков по трем скрещивающимся прямым, моделирует трехфазную область. Ее границами служат три гиперболических параболоида. Условия Δ m А =0, Δ m В =0 и Δ m N =0 задают три поверхности с общей вертикальной направляющей. Каждая такая поверхность пересекает один из гиперболических параболоидов по его криминанте. Крайние положения точек на криминантах соответствуют температурным интервалам превращений трехфазной реакции в двухфазную. Проекции контуров поверхностей на треугольник АВС задают множества составов, в которых может происходить изменение типа трехфазного превращения.

Работа выполнена при поддержке РФФИ (проект 05-08-17997-а)