Смешанная задача для нелинейного интегро-дифференциального уравнения, содержащего куб параболического оператора

В области D рассматривается уравнение

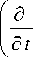
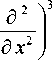
и ( t , x )

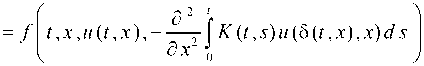
с условиями

" u ⁽ t , x ) | t e ( -„ ;0 ] = Ф 1 ⁽ t , x )’ u ⁽ t , x ) t e ( T ;© = ⁰ u t ⁽ t , x ) t = 0 = Ф 2 ⁽ x )> u tt ⁽ t , x ) | t = 0 ° 3 ⁽ x )>

" u ⁽ t , x ) x = 0 = u ⁽ t , x )| x = 1 = u xx ⁽ t , x )| x = 0 = ⁰,

_ uxx (t , x) x=1 = uxxxx (t , x) x =0 = uxxxx (t , x) x=1 = 0, где f (t,x,и(t,x)) e С(DxR2), здесь D = DT xD1, Dt =[ 0, T ], Dl =[ 0,1 ] ,0 < 1 <- ,0 < T <^ ;

0 <  K ( t , 5 ) e C ( D T ); 5 ( t , x ) * t ; ф i ( x ) e C ( D₁ ) , Ф i ^{( x} )| x = 0 =ф , ⁽ x )| x = 1 =ф ! ⁽ x )| x = 0 =Ф‘‘ ⁽ x ) x = 1 =Ф ^{(IV) (} x ) x = 0 = = ф (^IV) ( x ) x = 1 = 0, i = 1^3.

Решение данной задачи ищем в виде ряда [1]:

и ⁽ t , x ) = j^ a n ⁽ t ) ■ b n ⁽ x ), ⁽ t , x ) ^{e D} , ⁽⁴⁾ n = 1

где b n ( x ) = ^2 sinX _nx , здесь X _n = n. ^, n = 1,2, ....

Функции bn (x) удовлетворяют граничным условиям bn (0) = bn (1) = bn (0) = bn (1) = 0.

Следовательно, функция, определенная с помощью ряда (4), формально удовлетворяет условиям (3).

В данной статье все обозначения заимствованы из работы [2]. Норму в пространстве B p ^ ( T ) примем следующим образом:

II a(t) 11Bp :2 (T) = а (t) II a(t) 11 Bp (T) + n(t) IIх 2 a(t) 11B (T), где 0 <а(t); n(t) e C(DT), Xn = n.^ , n = 1,2, ....

Сведение решения задачи к счетной системе нелинейных интегральных уравнений. Введем следующее определение: если функция и ( t , x ) e E 2,'П, ( D ) удовлетворяет интегральному тождеству

T l I               д 3

Щ u ⁽ t , % ) — Ф + ^{3 t}

Tl

0 0

l

= J * -

д ⁴   ~ d ^{8 5}

------Ф + 3-----Ф + д t2 д x2       дtд x4

д ⁶ 1 . I . .

+--гФ + f Ф ddxdt = д x6             I

" д ² .1 Ф

.^д 1 ² J t - 0

l

l

3 J ф .

д ⁴

--7 Ф д x 4

д ³

■ Ф д t д x ²

d x +

- t - 0

для любого

dx

J t = 0

H ⁽ t , ^x ) ^e W k , p D _д 2 , то

t l X

JJ i E a n ⁽ s ) ■ b n ^{( x} ) 0 0 I n = 1

. д5

+3------ т

д s д x 4

Л 6

Ф+ф д x ⁶

д ³ i д ⁴

^{Ф +}     2    2

д s ³        д s ² д x ²

l

- f Ф } dxds = J ф ₁

Ф +

д ²

--7 Ф д t2

dx t=0

-

функция

l - 3 J * 2 0		Г д 3       1 , , 2 Ф д t д x 2		l dx + 3 J ф 3 t = 0             0	д x	4 Ф	dx . (6) t = 0
Пус	ть (	в л	(6)	Ф=Ф m ( t , x ) =		h ( t ) b m ( x ) e
e W k , p	D V	а 2 а x 2 ^	, где 0	* h ( t ) e С 3 ( DT ) .		Тогда

u ( t , x ) e E p 'П называется решением смешанной задачи (1)^(3) .

Теорема 1. Пусть выполняются следующие усло-

• 1)    fQ : B_p ( T ) ^ L_p ( D ) непрерывен;

• ²⁾    IP⁽ t )lI B p ( t ) <^X ;

• 3)    u ( t , x ) является решением смешанной задачи (1)^(3) и

• l

a n ( t ) = J u ( t , x ) b n ( x ) dx .

Тогда коэффициенты Фурье решения смешанной задачи (1)^(3) по собственным функциям b n ( x ) опе- д ²

ратора--- удовлетворяют следующей счетной д x ²

системе нелинейных интегральных уравнений (ССНИУ):

tl an (t ) = wn (t) + J Jf (s, x, Qa (s), Q 2 П a (5 (s, x) ))x

0 0

J J l ip a . ( s ) ■ b . ( x ) [- h -( s ) b m ( x ) - 3 X m h ■( s ) b m ( x ) -- 3 X m h ‘ ( s ) b m ( x ) + X 6 m h ( s ) b m ( x ) J-

• - f ( s , x , Qa ( s ), Q ², ⁿ a ( 5 ( s , x ) ) ) ■ h ( s ) ■ b m ( x ) } dxds = = J J | jE a n ( s ) ■ b n ( x ) [- h "( s ) - 3 X m h "( s ) - 3 X m h '( s ) + + X ⁶m h ( s ) J- f ( s , x , Qa ( s ), Q ²^ a ( 5 ( s , x ) ) ) x x h ( s ) ■ b_m ( x ) } dxds = 0.

Учитывая, что система функций { b_n ( x ) }    орто

) n = 1

нормирована, из последнего равенства имеем

T

J [ a n ( t ) ■ ( - h ^m( t ) - 3 X m h "( t ) - 3 X m h ‘ ( t ) + X m h ( t ) ) - 0

l

• - J f ( t , x , Qa ( t ), Q ^{2, n} a ( 5 ( t , x ) ) ) x

xh(t)■ bn(x)dx] dt = 0, x bn (x) Pn (t, 5) dxds, te DT ,        (5)

откуда, интегрируя по частям, получим где

w n ⁽ t ) =

14 -^

1 +x 2 t 2 1 ²U1 n +

T

J h ( t ) [ a n ( t ) + 3 X 2 a n ( t ) + 3 X 4 a n ( t ) + X n a n ( t ) -

t ²

1 ^--* ф 1

2 n 2 ' 3 n

■ e

X nt.

;

l

- J f ( t , x , Qa ( t ), Q ²' ⁿ a ( 5 ( t , x ) ) ) ■ b n ( x ) dx 0

dt = 0. (7)

P n ( t , s ) = 2 ■ ( t - s ) ² ■ e ^-X n ⁽ ‘ - s )

д ² t-

Q 'n a (t) =--- fK (t, s) u (s, x) ds = д x "

X t

= ^ X n J K ( t , s ) a n ( s ) ■ b n ( x ) ds .

n = 1      0

Так как h (t) - это любая функция, удовлетворяющая вышеуказанным условиям, то an (t) имеет обобщенные производные третьего порядка по t в смысле Соболева на отрезке DT. Поскольку h (t) * 0 для всех t e DT, то из (7) получим an(t) + 3X 2 an (t) + 3Xnan (t) + Xnan (t) =

Доказательство. Согласно определению решения смешанной задачи (1)^(3) имеем

l

= J f ( t , x , Qa ( t ), Q ²' ⁿ a ( 5 ( t , x ) ) ) ■ b n ( x ) dx . (8)

Решим систему (8) методом вариации произвольных постоянных:

a n ( t ) = ( C n + C 2 n t + C 3 n t ² ) • e "^X n t +

* j j / ( 5 , x , Qa ( 5 ), q ^{2 n} a ( 5 ( 5 , x ) ) ) x 0 0

x b n ( x ) P n ( t , 5 ) dxds , t e D t .         (9)

Для определения коэффициентов Cin (i = 1,3) используем условия an (0) = фin, an (0) = ф2n, an (0) = ф3n, где фin = jфi (x)■ bn(x)dx, i = 1,3, x e Dl. Тогда из (9) получим0 ССНИУ (5).

Однозначная разрешимость ССНИУ. Рассмотрим ССНИУ (5) при нелинейном отклонении 5 ( t , x ) = 5 ( t , x , u ( t , x )).

Теорема 2. Пусть выполняются следующие условия:

• 1)    j 11 / ( t , x , Qa°( t ), q ^2,n a⁰ ( 5 ( t , x , q a⁰ ( t >> ) ) || ⁰                                                                     L p ( D l )

dt < A < м ;

• ²⁾        У ⁽ t , ^x , u , ^9e Lip { ^{a (} t )_{| m} ; L 1 ⁽ t )_|s } , где

0 ( t ), L 1 ( t ) e C ( D t );

• 3)    5 ( t , x , u ) e Lip { L 2 , t ) | u } , где 0 <  L 2 , t ) e C ( D t );

• ⁴⁾    IP⁽ t )| P p n ₍ t ) <^m .

Тогда ССНИУ (5) имеет единственное решение в пространстве B²_р^ч_а ( T ).

Доказательство. Используем метод последовательных приближений:

a 0 (t) = Wn (t)> t e DT , akk+1(t) = Wn (t) +

< ti                                                   (10)

+j j/(5,x,Qak(5),Q2n ak (5(5,x,Qak(5))))x x b n(x)Pn(t,5)dxd5, k = 0,1,2,3,..., t e Dt .

В силу условий теоремы для первой разности a n ( t ) - a 0 ( t ) из(10)получим

II ^{a 1} < t ) ^{- a 0} < t >1 l , p ,_n<

< jP ( 5 - x , Q ^a"< 5 )• Q ²' ⁿ a ⁰ ( 5 ( 5 , x , Qa "( 5 )) ))| x 0 0

Lm         p ^p ^м,         q

PEIPn(t,5)| r ■[Elbn(x)| I dxd5< tl

< M 1 M 2 jj / ( 5 , x , Q_Cr°(5 ), Q ^{2 n} a ⁰ ( 5 ( 5 , x , Qa ⁰( 5 )) ) ) x 0 0

xdx d5 < M1M2 iq A , где M1=^^5axllP(t,5)lLp(t); M2=maxlb

1 1 1

—+—=1.

pq

Отсюда имеем, что

I^a'⁽t*^-a"<t’11.2_:S.t, <

<(a(t)M₁+n(t)M₁) M₂lqA,        (11)

где

t

П (t) = L 1(t) ■ j| K (t, 5) P( 1+ A^ L2,5))d5;

M, = max||x²Pa(t,5)      .

• ¹    (t,5’                         H.p(T’

С учетом (11) в силу второго и третьего условий теоремы для второй разности a2(t) - an (t) получим следующую оценку [2; 3]:

|| a2(t’-«1(t’ ||B2,a(T’ < (a(t’M1 +П(t’M1)M2 x j j|/ (5, x, Qa1,5), Q2,11 a1 (5, 5, x, Qa1,5))))-

0 0

-/(5,x,Qa°(5),Q2’n a0 (5(5,x,Qa0(5)))) |dxd5 < tl

<(a (t) M₁+n (t) M₁) M₂²jj

0 0

^a(5 ’ll^{a1 (5} ’^{-a0( 5} ’ I IB,

+

s

+L 1( 5) jK (5,0) I |x²(ai¹ (5 (0, x, q a¹,o))) -

- a⁰ (5(0,x,Qa⁰(0))))[ d0

dxd5<

(a (t) M₁+n (t) M₁)] ²M₂³l^q+11 ,     (12)

t где n(t) = L 1(t)■ j|K(t,5))■( 1+ A-L2,5))d5.

Для произвольного натурального числа k аналогично (12) получим

II^ak+1< t ’- ^ak (t ’I I, p’ <

(a (t ’ M1 +n (t ’ M1)] ‘⁺¹1 ’* kM 2^{2 k +1}k!.    (13’

Существование решения ССНИУ (5) следует из оценки (13), так как при k ^м последовательность {k ) м a (t)} сходится равномерно по t к > k=1

функции a (t) e B p, a (T). Покажем единственность этого решения в пространстве Bp'^ (T).

Пусть ССНИУ (5) имеет два решения: a (t) e Bp,a (T) и 9 (t) e Bp,a (T). Тогда для их разности получим оценку

IIa⁽t)-⁹⁽t)lIB2,_a(T)^-(^a(t)M^{1 +п(}t)M¹)^х

XM21 J|| a(5)-9(5)|IB2,_a(t) ds .         (14)

f                  d 2

+f I t,x,u^k(t,x), -——X

V                  d x

t xjK(t,s)uk(8(s,x,uk(s,x),x)ds Ф}dxdt -;

J^ф1

d2 _

—? ^ф d t²

dx + t=0

l

-³Jф3

l

³JФ 2

d⁴

--Ф d x4

d3 _

----7 Ф d t d x2

dx.

t=0

dx - t=0

Применяя к (14) неравенство типа Гронуолла-Бельмана, получим, что || a (t) -9 (t) || _{s 2 a (Г)}= 0 для всех t e [ 0; T ]. Отсюда следует единственность решения ССНИУ (5) в пространстве Bp^ (T).

Однозначная разрешимость смешанной задачи. Подставляя ССНИУ (5) в ряд (4), получим формальное решение смешанной задачи (1)^(3):

и (t, x) = £[ Wn (t) + n =1

tl

+JJ f (s,x,Qa (s),Q^2,aa(8(s,x,Qa (s))))х 0 0

X bn (x) Pn (t, s) dxds ]• bn (X).       (15)

Теорема 3. Пусть выполняются условия теоремы 2. Если 5 (t) e Bp(T) является решением ССНИУ (5), то ряд (15) будет решением смешанной задачи (1)^(3).

Доказательство. Так как 5 (t) e Bp'^ (T), то из равенства k limuk (t,x) = lim Van (t)• bn (x) = и (t,x) k^да             k^да n =1

следует, что f                   d2 ', limf t,x,uk (t,x),--у [k(t,s)uk(8(s,x,uk(s,x),x)ds = k - (            5 x ■ в смысле метрики Lp (D).

Строим последовательность функций:

V_k = JJ J u^k (t, x) 0 0 I

3                4                   56

d ;Ф ■ 3 ——-Ф + 3 -^Ф + ^Ф d t3      d t2 d x2      d t d x4

Покажем, что при k ^ да (17) есть интегральное тождество (6), т. е. lim Vk = 0. Интегрируя по частям k ^да отдельные слагаемые в (17) и учитывая условия теоремы и начальные условия an (0) = ф 1 n, a'п (0) = ф2n, an(0) = ф3n, имеем

f

Vk =Jh 1(x)-Еф 1 nbn(x)|[фttJ dx-0 V           n=i             J

f

^-J|^Ф2⁽x)-V 2 nbn⁽x) |^[ФtJ dx⁺

0 V             n=1               J

1 f             k               \

⁺Jh 3^(x)-V 3 nbn^(x) |[^Ф] ^{dx +}JJ^{Ф (}t , ^x) ^X

0 V             n=1               J       t=00 0

x£ ^JJf (t, y, Qa (t), Q²,^aa (8 (t, y, Qa (t))))• bn (y) dy -ⁿ=1 10

- f (t,x,Qa (t),Q21 a a (8(t,x,Qa (t))))}x x bn (x) dxdt.(18)

Очевидно, что первые три интеграла в (18) стремятся к нулю при k ^да, так как ф i (x )e Lp(Dl). Сходимость разности двух последних интегралов в (18) при k ^да следует из (16), откуда lim P_k = 0. k ^да

Это и доказывает теорему.