Смешанные дискретные модели в анализе упругих трехмерных неоднородных тел сложной формы

Как известно [1], при анализе трехмерных тел неоднородной (композитной) структуры широко используют микро- и макроподходы. В основе макроподхода лежат гипотезы, накладывающие определенные ограничения на поля перемещений, деформаций и напряжений тела, что порождает неустранимую погрешность в решениях. Кроме того, возникают трудности при реализации макроподхода в случае исследования трехмерных неоднородных, композитных тел сложной формы, особенно с малым коэффициентом наполнения неоднородностью. Это связано с тем, что в окрестности границы крепления тела или границы сложной формы гипотезы не выполняются, т.е. в окрестности данных границ тела реализуется трехмерное напряженное со- стояние. Микроподход дает возможность точно описывать поведение трехмерных композитных (неоднородных) тел сложной формы с любым коэффициентом наполнения неоднородностью. Однако конечноэлементный анализ таких тел с учетом их структуры сводится к построению базовых дискретных моделей очень высокого порядка, что создает проблемы при реализации метода конечных элементов (МКЭ) [2, 3, 4]. Базовые дискретные модели трехмерных тел, имеющих неоднородную структуру, состоят из однородных односеточных трехмерных КЭ первого порядка формы куба [2, 3]. Базовые разбиения учитывают неоднородные структуры и сложную форму тел и при этом порождают решения со сколь угодно малой погрешностью.

В данной работе предлагается совместное применение одно- и двухсеточного моделирования трехмерных упругих тел неоднородной структуры и сложной формы. Такое моделирование порождает смешанные дискретные модели, которые состоят из КЭ различной сеточной структуры: односеточных и двухсеточных КЭ. Подобласть тела, которая включает границу сложной формы или крепления тела, представляем базовым (мелким) разбиением, которое состоит из однородных односеточных КЭ первого порядка формы куба и учитывает неоднородную структуру и сложную форму тела, а остальную часть тела покрываем крупным разбиением на ДвКЭ неоднородной (композитной) структуры формы прямоугольного параллелепипеда. Мелкое и крупное разбиения склеиваем с помощью связующих ДвКЭ и в результате получаем смешанную дискретную модель, размерность которой меньше размерности базовой.

Для построения ДвКЭ формы прямоугольного параллелепипеда используем две вложенные трехмерные узловые сетки: мелкую и крупную. Мелкая сетка порождена базовым (мелким) разбиением ДвКЭ, которое состоит из однородных односеточных КЭ первого порядка формы куба и учитывает неоднородную структуру данного ДвКЭ. Построение ДвКЭ сводится к исключению параметров МКЭ в узлах мелкой сетки (которые не совпадают с узлами крупной сетки) с помощью аппроксимирующих функций перемещений u, v, w, построенных на крупной сетке, т.е. узловые перемещения мелкой сетки выражаются через узловые перемещения крупной сетки. Общее число узлов крупной сетки многократно меньше общего числа узлов мелкой, поэтому размерность ДвКЭ многократно меньше размерности его ба- зового разбиения. Существуют два типа ДвКЭ [5]. У ДвКЭ первого типа [5, 6] крупные сетки определяются только на границе его базового разбиения. Крупная сетка ДвКЭ второго типа определяется на всей его области. Изложены процедуры построения ДвКЭ второго типа и связующих ДвКЭ. Недостаток процедуры построения ДвКЭ первого типа состоит в том, что она содержит операцию вычисления обратной матрицы высокой размерности [5, 6].

Приведен пример расчета трехмерного тела сложной формы, имеющего неоднородную структуру.

1. Процедура построения двухсеточных конечных элементов

Изложение данной процедуры проведем для трехмерного ДвКЭ (второго типа) неоднородной структуры формы прямоугольного параллелепипеда размерами а х b х c , для рис. 1 имеем a = 12 h , b = c = 8 h . Считаем, что между компонентами неоднородной структуры ДвКЭ связи идеальны, а функции перемещений, напряжений и деформаций этих компонентов удовлетворяют закону Гука и соотношениям Коши [7]. Область ДвКЭ представляем базовым разбиением, состоящим из однородных односеточных КЭ V j первого порядка формы куба со стороной h [2], параметрами МКЭ которых являются значения перемещений u , v , w в узлах КЭ V j , j = 1,..., M ; M - общее число КЭ V j .

На рис. 1 показано базовое (мелкое) разбиение ДвКЭ на КЭ V j . Базовое разбиение ДвКЭ учитывает его неоднородную (композитную) структуру и порождает мелкую равномерную узловую сетку V hm размерностью m 1 х m ₂ х m 3 с шагом h по осям Ox , Oy , Oz . Для рис. 1 имеем т 1 = 13, т ₂ = т ₃ = 9. На мелкой сетке V h ^m определяем крупную трехмерную узловую сетку V размерности n 1 х n ₂ х n₃ с шагами: H 1 по оси Ox , H ₂ по оси Oy и H ₃ по оси Oz . Сетка V H вложена в мелкую сетку V hm , при этом имеем: H 1 = k 1 h , H ₂ = k ₂ h , H ₃ = k ₃ h, где k 1 , k ₂, k ₃ - целые, не менее 2. На рис. 1 узлы крупной сетки отмечены точками, H 1 = 3 h , H ₂ = H ₃ = 2 h , n 1 = n ₂ = n ₃ = 5, k 1 = 3, k ₂ = k ₃ = 2. Полную потенциальную энергию П_е ДвКЭ представим в матричном виде [8]:

M п e=У (2 qT [ кл- qTP)-                (d где [Kj ] - матрица жесткости; Pj ,qj - векторы узловых сил и неизвестных элемента Vj ; T - транспонирование.

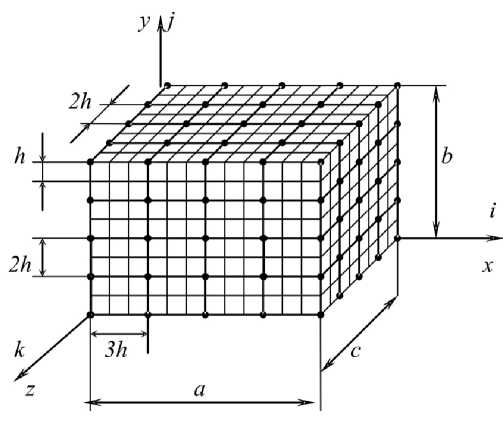
Рис. 1. Мелкая и крупная сетки ДвКЭ

С помощью полиномов Лагранжа [8] на крупной сетке VH определяем аппроксимирующие функции для перемещений u, v, w ДвКЭ, которые соответственно обозначим через uH, vH, wH и представим в форме n1 n 2 n з                             n n 2 n 3                              n1 n 2 n 3

Uh =Y£LNjuk - Vh =^£NA , Wh =^Niw . (2) i I j I k I                                      i I j I k I                                      i I j I k I где uijk, vjk, wjk - искомые значения функций uH, vH, wH в узле (i, j, k) сетки VH; i, j, k - координаты целочисленной системы координат ijk, введенной для узлов крупной сетки (см. рис. I); Nijk = Nijk(x- У- z) - базисная функция узла (i, j, k) сетки VH, i = I,...,nI, j=I,...,n2, k = I,...,n3, Njk = L( x) Lj( У) Lk (z), nI                                              n 2                                                Пз

Li ( x ) = П —T^ ’ Lj(У ) = П y^-^^ - Lk ( z ) = П —Д ’ (3) a= I, a* i x i x a               a= I, a* j y j y _a                a= I, a* k z k z a

( x i , y j , z_k ) - координаты узла ( i , j , k ) сетки V n в системе координат Oxyz .

Тройке целых чисел i , j , k узла ( i , j , k ) крупной сетки V H определим целое число Р и введем следующие обозначения: N ₃ = N_ijk , q ^ u = u_jk , q p = ^v i _jk , q p = w_jk , где Р= 1,—, n ₀; n О = n n 2 n 3 - Тогда выражения (2) примут вид

• ⁿ 0                           ⁿ 0                          ⁿ О

• ^u H = ^ N р q u , ^v H = ^ N з ^q p , ^w H = ^ ^N 3 q w -          ⁽⁴⁾

3= 1                      3= 1                      3= 1

Обозначим через qH = {q1 ,...,q“ , q1,...,qn^, qW,...,q^JT вектор узловых параметров МКЭ крупной сетки Vn, т. е. вектор узловых неизвестных ДвКЭ. Используя (4), компоненты вектора qj узловых неизвестных КЭ Vj выражаем через компоненты вектора qH , в результате получим равенство qj = [ Aj ] qH,                                (5)

где [ A j ] - прямоугольная матрица, j = 1,..., M .

Подставляя (5) в выражение (1), из условия 5 П e / d q_H = 0 получаем уравнение [ K_H ] q_H = F H ,

MM

[ K h ] = £ [ A j ] ^r [ K j ][ A ], F H = £ [ A ] ^r p .             (6)

j I                                                  j I где [KH ], FH - матрица жесткости и вектор узловых сил трехмерного ДвКЭ (второго типа) формы прямоугольной призмы, который обозначим через Veq, е - порядковый номер.

Замечание 1. Решение, построенное для крупной сетки ДвКЭ, с помощью формулы (5) проецируется на мелкую сетку базового разбиения ДвКЭ, что дает возможность вычислять напряжения в любом КЭ базового разбиения ДвКЭ, следовательно, определять напряжения в любом компоненте неоднородной структуры ДвКЭ.

Достоинства двухсеточных конечных элементов

• •    С помощью базового (мелкого) разбиения ДвКЭ учитывается его неоднородная и микронеоднородная структура.

• •    ДвКЭ порождают двухсеточные дискретные модели, общее число узловых неизвестных которых меньше общего числа неизвестных базовых моделей.

• •    ДвКЭ порождают решения, которые отличаются от решений, отвечающих базовым моделям, на заданную величину.

• •    С помощью варьирования соотношений шагов мелкой и крупной вложенных сеток ДвКЭ регулируется погрешность решений, построенных для двухсеточных дискретных моделей.

• •    Напряжения могут быть определены в любом компоненте неоднородной, микронеоднородной структуры ДвКЭ.

• •    Процедура построения ДвКЭ базируется на известных алгоритмах МКЭ и поэтому удобно реализуется на ЭВМ. Реализация МКЭ для двухсеточных дискретных моделей требует меньше ресурсов ЭВМ и временных затрат, чем для базовых моделей.

2.    Процедура построения связующих двухсеточных конечных элементов

Расчеты показывают [5], что ДвКЭ типа V eq (см. рис. 1) эффективны при анализе трехмерных тел, которые армированы ортогональными регулярными решетками волокон и область которых представляется ДвКЭ формы прямоугольного параллелепипеда.

При совместном применении одно- и двухсеточного моделирования тела неоднородной структуры подобласть V1 тела, которая включает границу крепления и границу сложной формы, представляем мелким разбиением, которое состоит из однородных односеточных КЭ первого порядка, а остальную часть тела (область V0) - покрываем крупным разбиением на ДвКЭ неоднородной структуры, V = V + V0; V -область тела. Мелкое разбиение области V учитывает неоднородную структуру и сложную форму тела. В результате получаем смешанную дискретную модель тела, состоящую из КЭ различной структуры. В смешанной дискретной модели тела связь мелкого разбиения области V с крупным разбиением области V0 осуществляется с помощью связующих ДвКЭ, которые обозначим через V^ (а - порядковый номер КЭ VS).

Рассмотрим процедуру построения ДвКЭ Vas. Пусть разбиение области V состоит из однородных односеточных КЭ Vj первого порядка формы куба со стороной h, т. е. область V1 представляем КЭ базовой модели тела. Связующий ДвКЭ Vas строим на основе ДвКЭ V/ , т. е. ДвКЭ Vass имеет такие же мелкую и крупную сетки, как и ДвКЭ Veq. Пусть связующий ДвКЭ Vas по границе Sa , которая лежит в плоскости yOz (рис. 2), соприкасается с областью V . На рис. 2 при x>12h показано разбиение тела на ДвКЭ Vas и Veq. Отметим, что на границе Sa сетка разбиения области V1 содержит узлы крупной сетки VH ДвКЭ Vas. Полную потенциальную энергию Пa ДвКЭ Vas представим в виде na=2дa)T [K] да- (дa)T pa. (7) где [KO; ] - матрица жесткости базового разбиения У^ ДвКЭ V^; Pha -вектор узловых сил и Дa - вектор узловых неизвестных разбиения Vhm. Вектор Дa имеет следующую структуру:

д a = { д a , q H , д а } T , (8) где д а - вектор значений перемещений тех узлов мелкой сетки V_h m ДвКЭ V a s , которые лежат на границе S _a и не совпадают с узлами крупной сетки V ; д ^а - вектор значений перемещений остальных узлов сетки V_h m , не совпадающих с узлами крупной сетки V ; q_H - вектор узловых неизвестных крупной сетки.

Используя (4), между векторами д ^a и q_H установим связь:

д a = [ D a ] q H , (9) где [ D _a ] - прямоугольная матрица.

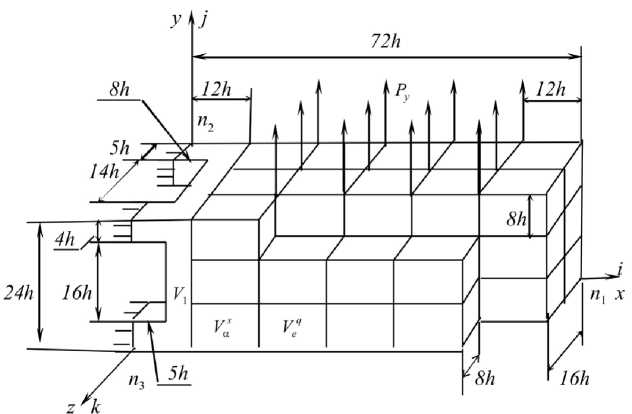
Рис. 2. Расчетная схема тела

С помощью (8), (9) построим равенство

△ Н = [Ba ] qH , здесь

q H : ^ 1 ^} ^г ,

[ ^ 1 1 0

[ B a 1 = 0 [ E 2 1 _ 0 [ D a 1

[E11, [E21 - булевы матрицы, qH - вектор узловых неизвестных связующего ДвКЭ VH, который граничит с областью V (см. рис. 2).

Применяя (10) в (7), из условия Э П S / 5 q H = 0 получаем формулы для вычисления матрицы жесткости [ K ^s _a 1 = [ B _a V [ K 1[ B _a 1 и вектора узловых сил F H = [ B _a V P H ДвКЭ V^s . Итак, ДвКЭ V H связывают мелкое разбиение области V с крупным разбиением области V ₀. В этом случае параметры МКЭ узлов мелкой сетки границы S _Н , не совпадающие с узлами крупной сетки V H (т. е. компоненты вектора А Н ), не исключаются и, следовательно, являются узловыми неизвестными связующего ДвКЭ V _a ^s .

Замечание 2. Обозначим: U0 - вектор функций перемещений базовой дискретной модели трехмерного тела (имеющего неоднородную структуру), которая состоит из однородных односеточных КЭ Vj первого порядка формы куба со стороной h. Пусть ||U-U0||<61, где U -точное решение. Пусть ||U0-Uh ||<6 , где Uh - вектор функций перемещений смешанной дискретной модели данного тела, т. е. состоящей из однородных односеточных КЭ Vj и двухсеточных КЭ V/ и V неоднородной структуры формы прямоугольного параллелепипеда. Тогда имеем ||U - Uh ||<60, где 60 =61 +6 . Погрешность 61 определяется параметрами базового разбиения тела. Факторы, влияющие на эту погрешность, изучены в теории МКЭ [9, 10]. Расчеты показывают, что погрешность 6 зависит от характерных геометрических размеров подобласти тела, которая представлена односеточными КЭ первого порядка, и от соотношения шагов мелкой и крупной вложенных сеток ДвКЭ Vq .

Достоинства смешанных дискретных моделей

• •    Размерности смешанных дискретных моделей трехмерных тел меньше размерностей базовых моделей.

• •    Смешанные дискретные модели учитывают неоднородную структуру и сложную форму трехмерных тел.

• •    Напряжения могут быть определены в любом компоненте неоднородной структуры смешанной дискретной модели трехмерного тела.

• •    Смешанные дискретные модели трехмерных тел порождают решения, отличающиеся от решений базовых дискретных моделей, на заданную величину.

• •    Реализация МКЭ для смешанных дискретных моделей трехмерных тел требует меньше ресурсов ЭВМ и временных затрат, чем для базовых моделей.

3.    Результаты численных экспериментов

Рассмотрим в декартовой системе координат Oxyz модельную задачу упругости для трехмерного упругого тела неоднородной структуры, которое имеет сложную форму (см. рис. 2). При x = 0 тело закреплено, т.е. имеем u = v = w=0. Граница крепления на рис. 2 показана штриховкой. Тело армировано ортогональной решеткой волокон с поперечным сечением 2h х 2h внутри области и 2h х h, hх h на границе. Расстояние между волокнами по оси Ox равно 10h, по осям Oy, Oz - 6h, т.е. волокна с поперечным сечением hхh являются ребрами ДвКЭ Va и Veq. Максимальное число волокон, параллельных оси Ox, равно 4, параллельных осям Oy, Oz, - 7. Базовая модель тела, состоящая из однородных односеточных КЭ Vj первого порядка формы куба со стороной h [2], учитывает его неоднородную структуру, сложную форму и порождает мелкую сетку Vh. Для узлов сетки Vh введена целочисленная система координат ijk; для рис. 2 имеем п1 = 73, n2 = n3 = 25. Тело нагружено силами Py =1,25 кг, которые приложены в узлах сетки Vh с целочисленными координатами (i, 25, к), где i =25, 37, 49, 61; к = 1, 9, 17. Модуль Юнга волокон равен 105 кг/см2, связующего материала - 104 кг/см2, коэффициент Пуассона для всей области тела равен 0,3; h = 0,5 см. Левый торец тела имеет вырезы: вертикальный -размерами 8h х 24h х14h и горизонтальный - размерами 5 h х16h х 5 h, которые порождают границу сложной формы. В связи с этим при построении смешанной дискретной модели для данного тела в области V1 (см. рис. 2), т. е. при 0 < x<12h, используем мелкое (базовое) разбиение, состоящее из однородных односеточных КЭ Vj первого порядка формы куба со стороной h. Остальная часть тела, т.е. при 12h < x < 72h, представлена крупным разбиением на ДвКЭ Veq и связующие ДвКЭ Vas, размерами 12hх8hх8h (см. рис. 1), е = 1,..., 30, a = 1,...,9. На рис. 2 показано разбиение тела на ДвКЭ Veq и Va.

Результаты расчетов представлены в табл. 1, 2. Анализ результатов показывает, что максимальное значение перемещений v h смешанной дискретной модели тела отличается от перемещений v ₀ базовой модели на 1,8 % (в табл. 1 максимальные значения перемещений v h , v ₀ выделены жирным шрифтом).

Эквивалентные напряжения о _h смешанной дискретной модели тела и о ₀ - базовой модели вычисляем в центре тяжести КЭ V j по четвертой теории прочности. Максимальное значение напряжения о _h отличается от напряжения о ₀ на 0,1 % (в табл. 2 максимальные значения напряжений о ₀, о _h выделены жирным шрифтом).

Таблица 1

Узловые перемещения (' = 25; v ₀, v h x 10 ⁴ см)

k \ i	13	25	37	49	61	73	v 0 , v h
	10,055	23,618	37,157	51,212	65,113	77,194	v 0
1	10,088	23,037	36,263	49,993	63,584	75,734	v h
	9,238	21,397	34,511	48,277	62,040	74,914	v 0
9	9,199	21,021	33,857	47,320	60,792	73,547	v h
	8,177	19,919	33,350	46,893	60,562	72,642	v 0
17	8,156	19,537	32,616	45,885	59,263	71,410	v h

Таблица 2

y	z \ x	0,5 h	1,5 h	3,5 h	4,5 h	6,5 h	16,5 h	о
		10,978	16,071	14,423	13,589	12,108	6,413	О 0
	0,5 h	10,958	16,054	14,426	13,602	12,141	6,652	о h
		5,543	1,952	1,725	1,561	1,280	0,668	О 0
	1,5 h	5,541	1,949	1,721	1,557	1,276	0,690	о h
0,5 h		3,872	2,355	1,998	1,793	1,348	0,548	О 0
	3,5 h	3,867	2,351	1,990	1,784	1,338	0,651	о h
		4,811	2,445	2,012	1,903	1,878	0,481	О 0
	4,5 h	4,812	2,442	2,003	1,890	1,855	0,568	о h

Эквивалентные напряжения ( с ₀, с h кг/см²)

Базовая модель тела содержит 114282 узловых неизвестных, ширина ленты системы уравнений (СУ) МКЭ равна 1956. Смешанная дискретная модель тела имеет 24834 неизвестных, ширина ленты СУ МКЭ равна 3567 и занимает в 2,5 раза меньше объема памяти ЭВМ, чем лента базовой модели. Время реализации МКЭ для смешанной дискретной модели тела в 2,3 раза меньше, чем для базовой модели.

Работа выполнена при финансовой поддержке РФФИ (код проекта 11-01-00053).