Смещённые эллиптические гауссовы пучки с внутренним орбитальным угловым моментом

При изучении световых полей особое место занимают поля, инвариантные к распространению в пространстве. Среди непараксиальных полей это, в первую очередь, плоские волны, пучки Бесселя [1], Матье [2] и параболические пучки [3]. Среди параксиальных полей это пучки Эрмита–Гаусса и Лагерра– Гаусса [4], Гауссовы пучки с произвольно расположенными оптическими вихрями [5], а также некоторые их суперпозиции [6, 7]. В [8] описана общая процедура расчёта параксиальных инвариантных к распространению полей с поперечным распределением интенсивности в форме произвольной замкнутой кривой.

В ряде задач, однако, некоторые преимущества получаются при использовании световых пучков с эллиптическим сечением. Например, как показано в [9], при передаче данных через турбулентную атмосферу использование эллиптических вихревых пучков позволяет уменьшить индекс сцинтилляции [10]. В [11] вихревым пучкам с дробным топологическим зарядом придаётся эллиптичность для увеличения производительности и информационной безопасности передачи данных. В [12] исследуются частичнокогерентные четырёхлепестковые эллиптические Гауссовы пучки в турбулентной атмосфере. Показано, что эллиптичность позволяет менять число лепестков при распространении. В оптической манипуляции мик- рообъектами вытянутое распределение интенсивности удобно для удерживания частицы вдоль одной координаты [13]. В [14, 15, 16] эллиптические Гауссовы пучки используются для увеличения производительности записи термохимических лазерно-индуцированных периодических поверхностных структур.

Интерес к эллиптическим пучкам побуждает к их аналитическим исследованиям. Параксиальное распространение светового пучка описывается интегральным преобразованием Френеля [17], ядро которого имеет вид экспоненты с квадратичным показателем, поэтому возможно аналитическое описание Гауссова пучка с произвольной эллиптичностью, углом наклона, положением центра, параболической кривизной волнового фронта. Такое описание есть в работе [18]. Однако свойством инвариантности такие пучки не обладают и при распространении в пространстве форма их поперечного сечения меняется. В нашей работе [19] были рассмотрены инвариантные эллиптические Гауссовы пучки с оптическим вихрем в центре и был установлен их орбитальный угловой момент. При распространении в пространстве такие пучки поворачиваются вокруг своего центра.

В данной работе мы рассматриваем параксиальные инвариантные к распространению эллиптические Гауссовы пучки (правда, пока без вихрей), аналогичные [19], но положение центра эллипса и его наклон к координатным осям может быть произвольным. Для этого мы составили непрерывную суперпозицию элементарных спиральных световых пучков [8] на плоскости и, решив нелинейную систему пяти уравнений для определения весовых коэффициентов этой суперпозиции, получили аналитическое выражение для распределения комплексной амплитуды. Также получена формула для орбитального углового момента таких пучков. Подобно теореме Штейнера в механике, он состоит из двух слагаемых. Одно из них (совпадает с выражением (4) в [20]) равно моменту относительно центра пучка и возрастает с его эллиптичностью. Второе слагаемое квадратично зависит от расстояния от центра масс до оптической оси. Оказалось, что ориентация эллипса в поперечной плоскости (угол наклона к координатным осям) на нормированный орбитальный угловой момент не влияет.

1. Инвариантные к распространению внеосевые Гауссовы пучки

В [8] (формула (6.1)) показано, что любая функция вида

1 f x2 + y2) / x ± iy )

E ± ( x , y , z ) = —expl--—I f\ -----I,         (1)

q I   qw0 J I qwo J где (x, y, z) – декартовы координаты, w0 – радиус перетяжки Гауссова пучка, q =1 + iz / z0, z0 = kw2/2 -расстояние Рэлея, k =2π / λ – волновое число света с

длиной волны λ, f ( x ± iy ) – произвольная целая аналитическая функция, является решением параксиального стационарного уравнения Гельмгольца (уравнения типа Шрёдингера):

d E d ² E d²E  „

2 ik— +---+---= 0 dz   5x2   dy2

и описывает световое поле, инвариантное к распространению в свободном пространстве, то есть форма поперечного сечения не меняется, а только увеличивается в масштабе и поворачивается.

Широкий выбор функций f (.) позволяет описывать оптические поля с самыми разными физическими свойствами. Например, если взять косинус:

1 | x + iy |

EI x, y, z ) = —cos l----— I exp q ( aoq J

x ² + y ² qw 0 ²

где α 0 – комплексный параметр, то получается косинусный вихревой пучок с распределением интенсивности в виде двух пятен (рис. 1 a,в ) и с бесконечным ТЗ, поскольку пучок содержит бесконечное число оптических вихрей (рис. 1 б,г) .

Если же вместо косинуса взять экспоненту, то есть рассмотреть пучок вида

E ( x , y , z ) = —exp ^q

x + iy a o q

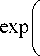
x ² + y ² qw 0 ²

з)

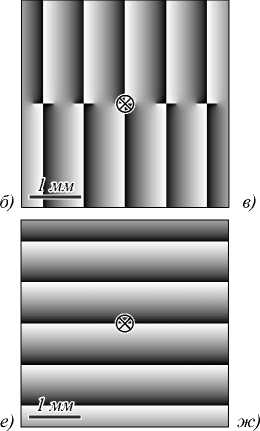
Рис. 1. Распределение интенсивности (а, в, д, ж) и фазы (б, г, е, з) вихревого косинусного пучка (3) и элементарного спирального пучка (4) в начальной плоскости (а, б, д, е) и на расстоянии Рэлея (в, г, ж, з) при следующих параметрах расчёта: длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w 0 = 0,5 мм, масштабирующий множитель α 0 = w 0 / 4, расчётная область |x|, |y| ≤ R, где R = 2 мм (в начальной плоскости) и R = 2 мм (на расстоянии Рэлея). Крест в центре показывает оптическую ось, вокруг которой происходит поворот дифракционной картины при распространении (на расстоянии Рэлея картина поворачивается на 45 градусов)

то логично ожидать, что вместо двух световых пятен получится одно. Такой пучок описан в [8] и назван элементарным спиральным пучком. В отличие от вихревого косинусного пучка с рис. 1а-г распределение интенсивности пучка (4) содержит одно внеосе- вое пятно (рис. 1д, ж), а ТЗ такого пучка равен нулю, так как пучок не содержит оптические вихри (рис. 1( f, h)). То есть замена в (1) косинуса на близкую в математическом смысле экспоненту приводит к пучку с кардинально иным распределением фазы.

Обозначим 1/ α 0 = [2 q /( w 0 ² | q | ² )] ( x c – iy c ), где x c , y c – вещественные числа (зависящие от z ). Тогда, выделив в (4) явно мнимую и вещественную части в экспонентах и разделив на постоянный множитель exp[( x c² + y c² ) / ( w 0 ² | q | ² )] = exp[| w 0 /(2α 0 )| ² ], перепишем (4) в виде:

w ₀

E ( x , y , z ) = —exp w

( x - xc )2 + ( y - yc )2 w2

+i w- (xcy - ycx) + 2R (x2 + y2) - iz где w (z), R (z), ζ (z) – ширина пучка, радиус кривизны волнового фронта и фаза Гоу на расстоянии z [4]:

z ²

w ( z ) = w 0,1 + — , z 0 ²

(   21A

R(z ) = z 1 +-- , V I z 2 /

( z I

Z( z) = arctan I

I z о )

Из (5) видно, что x c и y c – декартовы координаты максимума интенсивности (центра Гауссова пучка) на расстоянии z , связанные с координатами центра ( x c0 , y c0 ) в начальной плоскости следующим образом:

x c = ( w/w o )( x co cos Z- y co sin Z ) , y c = ( w/w о )( y co cos Z + x co sin Z ) .

Из (5) также видно, что поле представляет собой смещённый с оптической оси Гауссов пучок и к волновому фронту добавлена наклонная плоская волна, наклон которой согласован со смещением центра светового пятна и направлен перпендикулярно направлению от оптической оси до этого центра (рис. 1 д, е ). Это согласование обеспечивает инвариантность пучка при распространении в пространстве, благодаря которой расширение Гауссова пучка пропорционально его удалению от оптической оси.

Пучок (4), (5) является базовым для построения других инвариантных к распространению световых пучков. В случае совокупности таких пучков их оси лежат на однополостном гиперболоиде, ось которого совпадает с оптической осью, что и обеспечивает устойчивость составного пучка в целом. В [8] подробно рассмотрена процедура расчёта инвариантных пучков в форме плоской кривой. Так, например, формируя суперпозицию бесконечного числа пучков (5) с центрами (xc, yc), расположенными на отрезке или на эллипсе, можно получить инвариантный пучок соответственно в форме отрезка или эллипса (рис. 2). Если вместо эллипса взять окружность, то можно показать аналитически, что сложение пучков (5) вдоль окружности приводит (с точностью до коэффициентов) к однокольцевому (то есть с нулевым радиальным индексом) пучку Лагерра–Гаусса.

Ниже мы рассмотрим аналитически суперпозицию пучков (5), но не вдоль плоской кривой, как в [8], а на всей декартовой плоскости, и аналитически опишем внеосевой эллиптический Гауссов пучок, поворачивающийся вокруг оптической оси и инвариантный к распространению в пространстве.

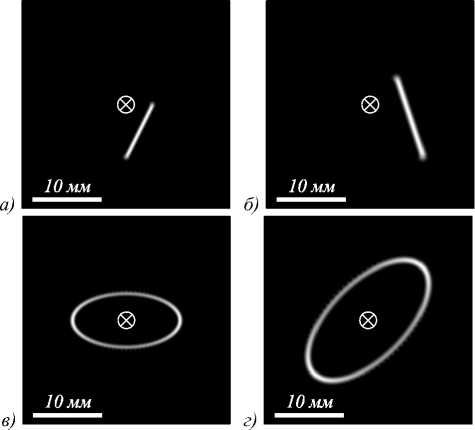
Рис. 2. Распределение интенсивности (а, в, д, ж) вихревого инвариантного пучка в форме отрезка (а, б) и в форме эллипса (в, г) в начальной плоскости (а, в) и на расстоянии Рэлея z = z 0 (б, г) при следующих параметрах расчёта: длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w 0 = 500 мкм, начальная точка отрезка (0, –15w 0 ), конечная точка отрезка (7,5w 0 , 0), горизонтальный радиус эллипса – 16w 0 , вертикальный радиус эллипса – 8w 0 , расчётная область на всех изображениях |x|, |y| ≤ R (R = 15 мм). Крест в центре показывает оптическую ось, вокруг которой происходит поворот дифракционной картины при распространении. Распределения в начальной плоскости получены сложением пучков (5) с центрами, расположенными вдоль отрезка или эллипса, а распределения на расстоянии Рэлея получены численно с помощью преобразования Френеля, чтобы подтвердить теорию

2. Структурно-инвариантные эллиптические Гауссовы пучки

С учётом (7), формула (5) может быть переписана в следующем виде (через координаты центра пучка в начальной плоскости):

E ( x , y , z ) = w ^exp - x ^{+ y} + ik- ( x² + y ² ) - w L    w ²    2 R

- i ^Z — ^c0 у ^c0 + ( x + iy ) ( x co - iy co ) .

w o ²     qwo               \

Рассмотрим непрерывную суперпозицию пучков (8), весовые коэффициенты которой находятся в квадратично-экспоненциальной зависимости от координат центров пучков:

w 0 E ( x , y , z ) = —exp w		"- x 2 _ w x c 2 0 x w 0 2 x exp	+ y 2 ik 1 x x\ + — ( x 2 + y 2 ) - v 2 1R (         )		(9)
+да +да - i Z ] x J J exp -да -да x c0 - 2 P x --2 P y w 0	[ _ Px y co w o _
			y c0 P yy — - 2 P xy w 0 2 x co + y co , + _      w o 2	x c0 y c0 2 w 0 2
+ 24 ( x + iy )(	x co -	iy co )	dx c0 dy c0 .
qw 0 2

Приведём подобные слагаемые в экспонентах в (9):

w 0

E ( x, y, z ) = —exp w

x ² + y ²     ik / ,

---+ — x2 + У2 - w2     2 R(       )

E ( x, y , z ) = C o exp ( - A xx u ² - Av ² - A xy uv - A x u - A y v ) , (14)

где

C o =

wo П wG

I „ 1 + P_a x 1 + Pyy x ^x exp l ^- i ^Z+ '  _t>-. +—^ Px²

I G G

A xx = 1 - iz o | q |² R ¹

A yy

A xy

= 1 - iz o | q |² R ¹

-

2 P xy        |

P x P y I , G      )

P xx - P yy - 2 iP xy G

P xx - P yy - 2 iP xy G

+да +да

- iZ] J J exp

-да -да

-

( 1 + P xx ) x4 - ( 1 + P, ) y w 0 ²             w 0 ²

2 i P xx ^- P yy ^{- 2} iP xy G

- ² p xy

x c0 y c0 w 0 ²

exp

2 I --l P x w 0 (

-

x + iy ।

I x c0 ^- qw o )

A x

- 2

= —x

G

x ^[ iP y ( 1 + P xx ) - P x ( 1 + P yy ) - iP xy ( P x + iP y ) J ,

w 0

P y ⁺ i

x + iy qw 0

y c0

dx c0 dy c0 .

Интеграл от экспоненты с квадратичным показа-

телем хорошо известен и потому

E ( x, y, z )

exp wG

x ² + y¹²

--— + w2

^ik / 2 2 \            ^{J 1 +} p xx

+— x² + y² - i Z exp< — x—

2 R^v       ' J I G

I . x + iy I xl p y + i -------I

(       qw o J

^{1 +} P yy

G

p x

2 x + iy I qw o )

-

2 P xy I — l P x

G \

-

x + iy if . x + iy 11 -------Il py + i-------I к qwo Д     qwo )l

где G =(1 + p xx )(1 + p yy ) – ( p xy ) ² .

В системе координат, повёрнутой на угол, равный фазе Гоу, и нормированной на ширину пучка w :

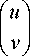
1 । cos Z sin Z 11 x w |- sin Z cos Z)| y

комплексная амплитуда равна

E (x, y, z ) = ww-G= exp [-u2 - v2 + izo |q|2 x x R1 (u2 + v2)- i ZJ exp Jl+pxx. [ py + i (u + iv )J +

,                     ¹ G                      (13)

+ ^P" [Px -(u + iv)]2-

- 2^ ^[ P x - ( u + iv ) __ P y + i ( u + iv ) Jl ,

или

- 2

A y = iG ^x

x ^[ iP y ( 1 + P xx ) - P x ( 1 + P yy ) - iP xy ( P x + iP y ) J .

Вещественные части этих коэффициентов определяют положение, размеры и ориентацию эллиптического светового пятна. Чтобы световое пятно было расположено в начальной плоскости в точке с координатами ( x 0 , y 0 ) (центр пятна), повёрнуто на угол α от оси x и имело размеры σ x и σ y (рис. 3), необходимо выполнение следующих условий (полагаем все коэффициенты суперпозиции p xx , p yy , p xy , p x , p y вещественными):

I, P xx - P yy I cos² a   sin² a

—11+-—y-^ I=----+----, wo I     G )   ex     Cy

^{1 f} 1 - P xxx__ ^P yy_ w 2 1       G ,

cos² a sin² a

--1--,

C 2      C 2

1 4 p xy w ₀ 2 G

<

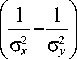
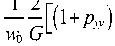
cos² a sin² a

C 2

C 2

I x - (16)

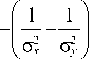
y _o sin2 a ,

1 2_Г/1 x -i    -f sin ² a cos ² a|

—-1 ( ^{1 +} P xx ) P y ^- P xy P x 1=- 2 1—^+I y o - w o G                  ^J I C 2      C y  J

-

1 I • . --x sin2 a . e2 o y J

Система (16) содержит 5 нелинейных уравнений, однако, как оказалось, её можно решить аналитически. Сложив первое уравнение со вторым, получим следующее условие:

112 --1--—-----.

^ 2 ^ 2 w 2

Оно означает, что из пучков (5) невозможно составить эллиптическое пятно произвольного размера. Поперечные размеры эллипса должны быть связаны соотношением (17), которое означает, что среднее степенное степени –2 [22] от этих размеров (то есть [(σ x ^–2 + σ y ^–2 ) / 2] ^–1/2 ) равно радиусу перетяжки w 0 элементарных спиральных пучков (4), (5), из которых строится суперпозиция. Далее будем называть w 0 эффективным радиусом перетяжки в том смысле, что эллиптический Гауссов пучок распространяется в пространстве с той же фазовой скоростью (фазой Гоу), что и круглый Гауссов пучок с радиусом перетяжки w 0 .

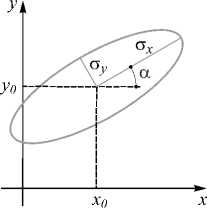
Рис. 3. Параметры эллиптического распределения интенсивности

Как оказалось, остальные параметры эллипса ( x 0 , y 0 , α ) могут быть произвольными и система (16) при любых их значениях имеет решение. Подставив найденные значения p xx , p yy , p xy , p x , p y в (13), получим:

а)

г)

E (x, y, z ) — —exp [-(1 - iz 0|q|2 R

।-i

-ц)u2 -

( 1 - iz 0 ^ |2 R ¹ + ц ) v ² + 2 i ц uv Jx                  (18)

x exp < -.

-2 x-(ц-1) + iy-(ц +1) (u + iv)- ic[,

_ wo           wo        J I

где ц —Ye-2 ia,(19)

Y — 1 - w — w -1.(20)

g2^

xy

Возвращаясь от координат (12) к исходным координатам, получим окончательное выражение для распределения комплексной амплитуды:

w 0

E ( x , y , z ) — —exp w

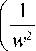
ik

-

2 R

^_e-2i Z w 2 e

-

-

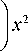
1 w ²

- ikL + X e - 2 - ^z ) y ² + 2 i ^ e - ² i ^z xy

2 R w ² J w ²

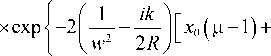
+iyo (ц + 1)J( x + iy)-iZ}.

x

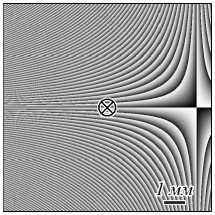
На рис. 4 показаны распределения интенсивности и фазы двух пучков (21) в начальной плоскости и на расстоянии Рэлея.

б)

в)

д)

е)

Рис. 4. Распределение интенсивности (а, в, г, е) и фазы (б, д) инвариантного внеосевого эллиптического Гауссова пучка в начальной плоскости (а, б, г, д) и на расстоянии Рэлея z = z 0 (в, е) при следующих параметрах расчёта: длина волны

λ = 532 нм, радиусы перетяжки Гауссова пучка σ x = 1425 мкм и σ y = 365 мкм (w 0 = 500 мкм) (а – в) и σ x = 4583 мкм и σ y = 355 мкм (w 0 = 500 мкм) (г – е), координаты центра Гауссова пучка (x 0 , y 0 ) = (2, 0) мм (а – в) и (x 0 , y 0 ) = (0, 7,5) мм (г – е), угол наклона большей оси эллипса к оси x α = π / 2 (а – в) и α = π / 4 (г – е), расчётная область |x|, |y| ≤ R, где R = 5 мм (а – в) и R = 15 мм (г – е). Крест в центре показывает оптическую ось, вокруг которой происходит поворот дифракционной картины при распространении. Распределения в начальной плоскости получены по формуле (21), а на расстоянии Рэлея получены численно с помощью преобразования Френеля и для сравнения тоже по формуле (21) (отличия визуально не видны). Область равномерной фазы (д) – область сверхмалой интенсивности, которую расчётная программа

не отличает от точного нуля

Из рис. 4 видно, что, действительно, после распространения в свободном пространстве распределения интенсивности изменились только масштабно и повернулись относительно начала координат.

Оба эти пучка при распространении приобретают такую же фазу Гоу, как у круглого Гауссова пучка с радиусом перетяжки w 0 = 500 мкм. Поэтому суперпозиция таких пучков также распространяется без изменения своей формы.

Например, из таких пучков можно составить инвариантную к распространению двухлепестковую суперпозицию. Такие пучки используются в микроскопии отдельных молекул и для улучшения продольного разрешения в изображающих системах [23]. На рис. 5 показаны распределения интенсивности и фазы двухлепесткового пучка, составленного из двух противоположных эллиптических Гауссовых пучков (21) в начальной плоскости и на расстоянии Рэлея.

Рис. 5. Распределение интенсивности (а, в) и фазы (б) инвариантного двухлепесткового пучка в начальной плоскости (а, б) и на расстоянии Рэлея z = z 0 (в) при следующих параметрах расчёта: длина волны λ = 532 нм, радиусы перетяжки двух противоположных эллиптических Гауссовых пучков σ x = 1617 мкм и σ y = 362 мкм (w 0 = 500 мкм), координаты центров пучков (x 0 , y 0 ) = (±2,5, 0) мм, угол наклона большей оси эллипса к оси x α = 0, расчётная область |x|, |y| ≤ R (R = 5 мм). Крест в центре показывает оптическую ось, вокруг которой происходит поворот дифракционной картины

при распространении

Аналогично можно располагать эллиптические пучки на окружности для передачи информации. Например, если 16 эллиптических Гауссовых пучков расположены на окружности и используются для передачи двух байтов, то число 27000 (в бинарной системе 0110100101111000) может передаваться пучком, показанным на рис. 6.

Как видно из рис. 6, на расстоянии Рэлея данный пучок повернулся на 45 градусов, а в дальней зоне – почти на 90 градусов, но форма у него не изменилась и остаётся такой же, как в начальной плоскости. При этом если в начальной плоскости не задавать поле (21) со специально подобранной фазой, а задать суперпозицию эллиптических Гауссовых пучков с распределением интенсивности, показанным на рис. 6 а, д , но с плоским волновым фронтом, то в дальней зоне распределение интенсивности искажается из-за взаимодействия Гауссовых пучков между собой (рис. 6 г, з ).

3. Энергия и орбитальный угловой момент

Энергия и орбитальный угловой момент произвольного параксиального светового поля находятся по следующим формулам [21]:

W — J J E * ( x , y ) E ( x , y ) dxdy , -да -да

J z — Im J да E * ( x , y ) x

-да -да

dE (x, y)    dE (x, y )]

x x— -- - - y— --- dxdy .

dy         5x

Подставив в эти формулы комплексную амплитуду (21), получим выражения для энергии и ОУМ внеосевого эллиптического инвариантного пучка:

W = ^{n w 2} exp J 2^-f  1

J z = 2 r°- ( 1 -Y cos w 0 ²

( 2 _Ф о - 2 a ) ] ^ , (24)

n w2Y | Y

2^1 -Y ² 1 ^{1 -} Y ²

20) W +

+ 2—cos20 lx w2       J

Разделив ОУМ на энергию, получим нормированный ОУМ:

2 | . (26)

Jz _ r² Y ² _ ₉ r ² , 1 1 о y g x

— 21— 211

W w 2 1 -Y ²     w 0 ² 4 1 о x о y

Как видно из (26), при смещении пучка от оптической оси нормированный ОУМ возрастает квадратично с расстоянием r 0 , что согласуется с теоремой Штейнера. Также из (26) видно, что на ОУМ влияет эллиптичность пучка, но его наклон к осям координат на ОУМ не влияет. При r 0 =0 приведённое выражение совпадает с полученным в [19].

Численный расчёт подтверждает формулу (26). Так, для пучка на рис. 4 а-в теоретическое значение ОУМ равно 35,328. При численном расчёте по формулам (22) и (23) получены значения 35,022 в начальной плоскости (рис. 4 a ) и 34,881 на расстоянии Рэлея (рис. 4 в ). Для более узкого пучка на рис. 4 г-е теоретическое значение ОУМ равно 491. При расчёте получены значения 420 в начальной плоскости (рис. 4 г ) и 392 на расстоянии Рэлея (рис. 4 е ). Более

существенная ошибка для пучка с рис. 4г-е объясняется его более близким расположением к краям рас- чётной области, благодаря чему в расчёт ОУМ не включена периферийная область, влияющая на ОУМ.

а)

б)

в)

г)

ж)

е)

з)

д)

Рис. 6. Распределения интенсивности двух суперпозиций инвариантных внеосевых эллиптических Гауссовых пучков в начальной плоскости (а, д), на расстоянии Рэлея z = z0 (б, е) и в дальней зоне z = 3z0 (в, ж), а также распределения интенсивности в дальней зоне аналогичных суперпозиций эллиптических Гауссовых пучков, но без специально подобранной фазы (то есть не инвариантных) (г, з) при следующих параметрах расчёта: длина волны λ = 532 нм, радиусы перетяжки Гауссова пучка σx = 2500 мкм и σy = 357 мкм (w0 = 500 мкм), координаты центров Гауссовых пучков

(x 0p , y 0p ) = (r 0 cos φ p , r 0 sin φ p ) (r 0 = 5 мм, φ p = 2πp / 16, p = 1, 2, 4, 7, 9, 10, 11, 12), углы наклона больших осей эллипсов к оси x α p = φp (а – г) и α p = φp + π / 6 (д – з), расчётная область |x|, |y| ≤ R, где R = 15 мм (а, б, д, е) и R = 25 мм (в, г, ж, з).

Крест в центре показывает оптическую ось, вокруг которой происходит поворот дифракционной картины при распространении. Распределения в начальной плоскости получены по формуле (21), а на расстоянии Рэлея и в дальней зоне получены численно с помощью преобразования Френеля

Заключение

Хорошо известно, что световые поля, которые распространяются без изменения своей структуры (инвариантные к распространению), имеют бесконечную энергию. Примеры таких полей известны: плоская волна, пучки Бесселя, пучки Матье. Любые другие инвариантные поля можно построить с помощью известного преобразования [24]:

2 п

E ( x,y ) = J A ( ф )ехр [ ik ( x cos Ф + y sin ф ) ] d Ф , 0

где A (φ) – произвольная функция от угловой полярной координаты (периодическая с периодом 2π).

Лазерные пучки с конечной энергией могут быть только структурно-инвариантными, то есть сохранять при распространении только структуру распределения интенсивности и изменяться масштабно, и вращаться.

Впервые такие пучки (авторы их назвали спиральными пучками) были рассмотрены в 1993 году [8]. У таких пучков, смещенные они с оптической оси или нет, все винтовые сингулярности должны быть одного знака (1). Если в пучке винтовые сингулярности разных знаков, то при распространении такой пучок изменяет (сильно или не сильно) свою структуру [25]. В нашей работе структурная устойчивость эллиптического пучка (21) обеспечивается тем, что он являет- ся суперпозицией (9) структурно-устойчивых (спиральных [8]) пучков (5).

Таким образом, в данной работе, рассмотрев непрерывную суперпозицию элементарных спиральных световых пучков [8] на плоскости и решив систему из пяти нелинейных уравнений для определения весовых коэффициентов этой суперпозиции, мы получили аналитическое описание параксиальных инвариантных к распространению в пространстве эллиптических Гауссовых пучков, смещённых с оптической оси (формула (21)).

При распространении такой пучок поворачивается, но не относительно своего центра, а относительно оптической оси. Оказалось, что смещение центра такого эллиптического пучка и его ориентация в поперечной плоскости могут быть произвольными, но радиусы перетяжки связаны между собой так, что среднее степенное степени –2 [22] от этих двух радиусов перетяжки равно радиусу перетяжки круглого Гауссова пучка, распространяющегося с той же фазовой скоростью (с той же фазой Гоу) (17).