Смеси вероятностных распределений в задачах регрессии и проверки на аномальность и их применение для PVT-свойств

Нормальное распределение часто возникает в различных задачах анализа данных и достаточно хорошо изучено с точки зрения теории. Тем не менее оно имеет легкие хвосты распределения, что является серьезным недостатком при оценке параметров моделей, основанных на нормальном распределении. Если в данных присутствуют выбросы, что часто происходит в реальных данных, то оценки параметров оказываются сильно смещенными в сторону выбросов. Для устранения этого недостатка часто рассматривают распределение Стьюдента (или Т-распределение), которое имеет свойства, похожие на свойства нормального распределения, но при этом имеет тяжелые хвосты. Тем самым распределение Стьюдента обладает некоторой степенью устойчивости к выбросам.

Свойства распределения Стьюдента впервые исследовал Уильям Госсет, который опубликовал свою работу под псевдонимом Student. Госсет обратил внимание, что стандартизированное (отцентрированное и отмасштабированное) выборочное среднее нормальной выборки при замене неизвестной дисперсии на ее оценку уже имеет распределение, отличное от нормального [1]. В литературе приводятся некоторые свойства распределения Стьюдента, например, вычисляется плотность распределения при его определении через комбинацию случайных величин, имеющих нормальное распределение и гамма-распределение, его математическое ожидание и дисперсия (см., например, [1] и [2]). Естественным образом подобно нормальному распределению вводится многомерный аналог распределения Стьюдента [3]. Вычислительные методики приближенного вычисления характеристик распределения Стьюдента подробно разобраны в книге [4]. В статье [5] показано, что условное распределение компонент вектора, имеющего многомерное распределение Стьюдента, также имеет распределение Стьюдента. Нами же в разделе 3 в силу удобств для полноты изложения приводится доказательство этого утверждения. Некоторые теоретические свойства используемых распределений приведены в разделе 2.

Для описания данных часто используют смеси нормальных распределений. Оценка параметров такой смеси происходит с помощью ЕМ-алгоритма [6]. Описание ЕМ-алгоритма и некоторые теоретические свойства смеси распределений приведены в разделе 4. При наличии выбросов в данных логично рассматривать смесь распределений Стьюдента. Идеи оценки параметров смеси распределений Стьюдента были описаны в [7], [8] и [9]. В частности, в [7] приведены формулы условного ЕМ-алгоритма. В данной статье в разделе 5 приводится полный вывод метода оценки параметров при помощи похожей вариации ЕМ-алгоритма, в которой на Е-шаге применяется вариационный байесовский вывод (см. [6]). Оценку параметров смеси распределений Стьюдента можно также производить с помощью методов МСМС [10].

Рассматриваемая вероятностная модель для описания данных имеет множество практических применений, что позволяет ее гибко настраивать и проводить широкую аналитику данных. Перечислим приложения, которые подробно разобраны в разделе 6:

• 1)    Кластеризация точек на выбранное количество кластеров.

• 2)    Выявление аномальных точек.

• 3)    Регрессия для предсказания любого набора вещественных признаков, используя любой другой набор признаков. Помимо самого предсказания можно вычислять предсказательный интервал, а в общем случае — распределение.

• 4)    Работа с пропусками в данных.

2.    Распределения 2.1.    Нормальное распределение

Такое большое количество приложений обусловлено тем, что модель смеси распределений является генеративной, поскольку она описывает совместное распределение всех признаков. Это распределение позволяет также генерировать искусственные данные. Среди недостатков модели можно отметить ее применимость только к вещественным признакам.

Модель смеси распределений можно рекомендовать для применения в задачах, в которых стоит ожидать непрерывную зависимость признаков друг с другом, например, в задачах естественных наук. Зависимость при этом не обязана быть линейной. В разделах 7 и 8 продемонстрировано применение модели к данным PVT-свойствам пластовых флюидов, на которых модель показала высокое качество при сравнении с широко известными моделями машинного обучения. Кроме того, полученные моделью результаты не противоречат физическим законам в отличие от многих методов машинного обучения, в частности, основанных на решающих деревьях.

В настоящем разделе приводятся определения и некоторые базовые свойства нормального распределения и распределения Стьюдента, которые лежат в основе разработанной модели. Также приводятся свойства гамма-распределения, с помощью которого можно представить распределение Стьюдента в удобном для исследований виде. Все утверждения данного раздела можно найти, например, в литературе [1], [2], [3], [5], [6], [11].

Плотность многомерного нормального распределения с центром в точке д G Ra и симметричной неотрицательно определенной невырожденной матрицей ковариаций У вычисляется по формуле

9(ж|Д, У) =

ОЩсаЛТр 2(l д)ТУ-1(ж д)) •

Всюду далее будем использовать это обозначение для плотности нормального распределения.

Рассмотрим матрицу В — корень из матрицы У, то есть удовлетворяющую условию В В^т = У. Тогда если £ имеет распределение N" (0, Ід) г де 1^ — единичная матрица размерности d. то д = д + В^ имеет распредслспис JV (д, У).

2.2.    Гамма-распределение

Плотность гамма-распределения Г(а,3) имеет вид а3

7(ж|а,3) = ——ж³ 1 е І {ж > 0}. ^Г(3)

Всюду далее будем использовать это обозначение для плотности гамма-распределения.

Заметим, что величина  1/а  является параметром масштаба, поскольку

7($1«,3 ) = а7(аж|1,3)- Таким обр>азом. если £ — Г(а,3)- то а^ — Г(1,3) я а^/3 — Г(^,^).

Пусть £ — Г(а,3)- Извести о [1], что Е£ = 3/а. Посчитаем математические ожидания некоторых величин, которые пригодятся в дальнейшем

/ /3

^{1n ж} • од ^ж ^ “^$dx = од

+ ^

I (ln у — lna) • у^3- 1е-^ydy =

dr(3)/d3 - Г(3)1па Г(3)

3(3 ) — 1n а,

где 3(ж) = ^а^^Р) — дпгамма-фупктщя. При 3 >  1 также получаем

+ ^

J Г(3)^{ж   е}

-

“^$dx =

I 8—2        аГ(3 — 1) а

J ^у3 2 ^е «^dy = -ГІ3)- =    1•

2.3.    Распределение Стьюдента

Распределение Стьюдента имеет параметр v — число степеней свободы. Чем меньше значение количества степеней свободы, тем более тяжелыми хвостами обладает распределение Стьюдента, и тем оно более устойчиво к выбросам. Кроме того, нормальное распределение является предельным распределением Стьюдента при стремлении числа степеней свободы к бесконечности.

Многомерное распределение Стьюдента с v > 0 степенями свободы, с вектором средних д G R^ и симметричной неотрицательно определенной невырожденной матрицей масштаба У обозначим T_v (д, У). Плотность этого раопределения в точке ж G R^d вычисляется по формуле

?(ж1д, у,р) =

Г ()

F(v/2)v ^2тД/2|У|1/2

1 + - (ж — д)тУ 1(ж — д)

i/+d

Утверждение 1. Пусть случайный вектор £ и случайная величина д независимы и имеют распределения N (0, У) и F(v/2,v/2) соответственно, ад G R'^ некоторый фиксированный вектор. Тогда случайный вектор X = д + ^/^Д имеет распределение Стьюдента с v степенями свободы, вектором средних д и матрицей масштаба У.

Плотность распределения Стьюдента можно представить в интегральном виде:

Р(ж|д, У,v)= / 9(ж|д, У/-)7Ы-/2, v/2)d-.

"о

Докажем утверждение. На основании обобщенной формулы свертки [11] плотность вектора X можно представить в виде интеграла нормального и гамма-распределения. Выпишем и преобразуем этот интеграл

+^

Р(ж|д, У,v)= / 9(ж|д, У/-)7Ы-/2, v/2)d- = о

= / ----- ^- / , ежр (—^-(ж — д)^тУ^-1(ж — д)) •

(Г/v/₂) -^v/2 1^ежР^(—v-^72)d- =

0 (2лД/2Д5е1у       2

(v/2)v/2 (27d/2F(v72)Vdety

+^

У у^+сі)/2-1ежр (—2 [v + (ж — д)ТУ-1(ж — д)]) d-. о

Обозначим А = v + (ж — д)^т У 1(ж — д) и сделаем заме ну переменных г = Ау/2:

(v/2)v/2 (27d/2F(v72)Vdeiy

,;. 2 '     ) ^/^«я» (—г) dz =

о

[v + (ж — д)тУ 1 (ж — д)] (v+c/)/2 =

Докажем утверждение. Рассмотрим X = р + е/Д?’ где случайный вектор £ ~ Ы (0, У) и случайная величина р ~ r(v/2, v /2) независимы.

EX = р + E^/VT = р + ЕеЕр-1/2 = р, поскольку Ер-1/2 существует и вычік/ляется аналогично Ер-1.

DX = E(X — р)(X - р)^т = Е^^^т /р = Е^^^т Ер^-1 = De • '., 2 = У. VI 2 — 1 V — 2

Утверждение 3. Пусть случайный вектор £ и случайная величина р независимы и имеют распределения Ы (0, У) и Г(а/2,3/2) соответствеппо. Тогда случайный вектор X = р+е/Др имеет распределение Стьюдента с 3 степенями свободы, вектором средних р и матрицей масштаба. а.У/3-

Докажем утверждение. По упомянутым ранее свойствам гамма-распределения случайная величина, р = ар/3 имеет распредел сипе Г(3/2,3/2).

x=р+-4 уз

= ^{р +}

е У ^ТЗ е

= р +

У «р/3     ур где е = еУ«/3 имеет распредслспис Ы(0,аУ/3)- Таким образом, вектор X тоже имеет распределение Стьюдента, с указанными выше параметрами.

Утверждение примечательно тем, что рассмотрение разных параметров гамма-распределения при определении распределения Стьюдента, является избыточным и не расширяет класс распределений.

2.4.    Маргинальные распределения

Пусть а,Ь~ пспсросокаюшнося множества индексов, причем a U b = {1,...,d}. Без ограничения общности считаем, что a = {1,...,d_a},b = {d_a + 1,...,d},db = d — d_a. Векторы и матрицы представим следующим образом:

ХД /рЛ /У„„ УаД

Х = W , р = Ц , УУТь Уьь) , где Xa G Rd“,Xb G Rdb,ра G Rd“,рь G Rdb, Уаа G R^*^, у^ь е Rdaxdb, Уьь Е Rdbxdb. Известно следующее свойство.

Утверждение 4. Пусть случайный вектор X имеет нормальное распределение Ы (р, У). Тогда случайный вектор Х_а также имеет нормальное распределение Ы(р_а, Уаа)-

Утверждение 5. Пусть случайный вектор X имеет распределение Стьюдента 7^(р, У). Тогда случайный вектор X_a также имеет распределение Стьюдента 7^(р_а, У_а).

Докажем утверждение.

+ ^

р(Ха) = J p(x_a,Xb)dx_b

+ ^

ДЖ а ,Ж ь |р, У/р^Хь

R ^d b

= / / ⁹(^ж “ ,^ж ь |р, У/у)й(y|v/2, v/2)dydж ь =

R ^d b 0

+ ^

7 ⁽P ^{| v/2, v/ 2) d}P = J q^(xа\Pа^{, y}aa^/y⁾P⁽y^lv/2,v/2)dy,

Внутренний интеграл получен на. основании того, что компоненты нормального вектора, также имеют нормальное распределение согласно утверждению 4.

3.    Условное распределение

Модель смеси вероятностных распределений позволяет построить регрессионную зависимость на произвольные признаки с помощью условного распределения. В утверждении б приводятся формулы для параметров условного распределения для нормального случайного вектора, а в теореме 5 — для случайного вектора, имеющего распределение Стьюдента.

Пусть случайный вектор X имеет нормальное распределение Ы(ц, У), где У — невырожденная матрица масштаба. Пусть также a,b,c — непересекающиеся множества индексов, причем a U b U c = {1,...,d}. Без ограничения общности считаем, что а = {1,..., da}, b = {d_a + 1,..., d_a + db}, c = {d_a + dь + 1,..., d}. Векторы и матрицы представим следующим образом:

X =

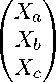
ц =

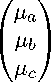
У =

Уаа

УТь

Тас

УаЬ

Уьь

УТс

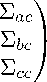
Обозначим также

Л=(

' Лаа . ЛТь

Лаь\ _ /Уаа

ЛЬЬ       УТь

УаЬ

Уьь

)

Утверждение 6. Вектор Ха при условии Хь имеет условное распределение Ы(ц, У), для которого параметры вычисляются по формулам

Ц = Ца - Л-а1Лаь(Хь - Ць), У = Л-1

Доказательство этого утверждения приводится в книге [12]. Из него следует, что условное распределение компонент нормального вектора также нормальное. Рассмотрим теперь случай, при котором вектор X имеет распределение Стьюдента Т_Р(ц, У).

Теорема 5. Вектор Х_а при условии Хь имеет условное распределение Тр(ц, У), для которого параметры вычисляются по формулам

V = V + (1ь, ц = ца - Лаа Лаь(Хь — №), У = ---"ТГ^Лаа1 ’ v + dь где

^{т(х)   (х ц}ь) (^Льь ^Л_аь^Лаа ^Лаь) ^{(х ц}ь^).

Замечания. Функция т(х) неотрицательна, поскольку все угловые миноры матрицы Льь — ЛТьЛ^-а1Л_аь положительны в силу формулы определителя блочной матрицы [13] и положительной определенности матрицы масштаба.

Докажем утверждение. При преобразовании формул плотности будем использовать знак пропорциональности выражений по х_а, опуская слагаемые, которые не зависят от х_а. По утверждению 5 получаем

Р(ХаХ) К р(Ха,Хь) =    q(Хa,Хь\ц^Q'^Ъ, ^/уУ^М^/^ду,

™ ■ = (ца) •=^аь = (Ут

У аь У ьь

^. Внутренний интеграл получен на основании того, что компоненты нормального вектора также имеют нормальное распределение. Вычислим произведение матриц, стоящих в ления

показателе

экспоненты плотности нормального распреде-

Л Ха — цаА ^Т Л Хь — ць

Лаа . ЛТь

Лаь Льь

Л / Ха — Ца\ = ) \Хь — ць)

= ^(ха ^- ра^ ^Лаа(Ха ^- ра) + ^{2( х} а ^- р а) ^ЛаЬ(^ХЬ ^— рь ) + (^ХЬ ^— рЬ^^ЬЬ^Ь ^— р ь ) ^—

• —    ^ха ^Лаа^ха ^2ха (^Лаа^ра ^ЛаЬ(^ХЬ  ^р Ь )) + ^ра ^Лаа^ра + ^(хЬ ^рЬ ) ^Л ЬЬ ^(хЬ ^р Ь ) ^2ра ^ЛаЬ^(хЬ  ^рЬ) —

— ^ха ^Лаа^ха ^{2 х} а ^Л аа (^р а ^Л аа ^ЛаЬ^(хЬ ^р Ь )) +

+ (^р а ^— А^-^АаЬ^(хЬ ^{— р} Ь )) ^Лаа (^ра ^{— Л-}а ^ЛаЬ^(хЬ ^{— р} Ь )) + ^ ^{( х} Ь ) ^—

(ха [ра Лаа ЛаЬ(хЬ   рЬ)]) Лаа (ха [ра Лаа ЛаЬ(хЬ рЬ)]) + р(хЬ), где

^{р ( х} Ь) — ^ра ^Лаа^ра + ^(хЬ ^рЬ) ^ЛЬЬ^(хЬ ^рЬ) ^2ра ^ЛаЬ^(хЬ ^рЬ)

(^р а ^Лаа А_аЬ^(хЬ ^р Ь )) ^Лаа (^а ^Лаа ^ЛаЬ^(хЬ ^р Ь )) —

• —    ^(хЬ ^рЬ) ^ЛЬЬ^(хЬ ^рЬ)  ^2ра ^ЛаЬ^(хЬ ^рЬ)  ^(хЬ ^рЬ) ^ЛаЬ^Лаа ^ЛаЬ^(хЬ ^рЬ⁾+^2ра ^Лаа^Лаа АаЬ^(хЬ ^рЬ) —

^(хЬ ^рЬ) ( ^Л ЬЬ ^ЛаЬ^Лаа ^Лаь) ^(хЬ РЬ)*

Подставляем полученное выражение в интеграл

+ ^

р(ха |х ь ) к У д(ха,х_ь1р^аЬ, Т°^ъ/у)^(-y\v/2₁v/2')dy tx

+                              ^

• 2 у ^хь   ^рь А_аь   ^л ьь ^хь ^рь

+ ^

• ^—    у^-а/2е^хр ^ ^— 2 (^ха ^— [^ра ^{— Л}-а1^ЛаЬ^(хЬ^{— р}Ь)])  ^Лаа (^ха ^— [^ра ^{— Л}_аа^1ЛаЬ^(хЬ ^{— р}Ь)])^  ^х

4.    Смесь распределений 4.1.    Свойства смеси распределений

+ ^

_х у (^+ ^-ь )/ ^2-1ехр (^—у ^ ^М ) Ду ^x j ₉ ^{( х} „ \^р, К^-а1/у)^⁽у\а/²,Р^/2)ау, 0

где а — v +^(хь) и 3 — v+db- По формуле свертки и утверждению 3 эта плотность является плотностью распределения Стьюдента с v — v + d^ степенями свободы, вектором средних р — ра — Л-ДаЗХь — рь) И матрицей масштаба 5 — ^⁺^т+З^р) Л-¹.

В данном разделе формально вводится понятие смеси вероятностных распределений и доказываются ее свойства, необходимые для решения обозначенных ранее задач машинного обучения. Кроме того, приводятся итерационные методы оценки параметров смеси нормальных распределений и смеси распределений Стьюдента.

Рассмотрим смесь вероятностных распределений

к

• ^{P —} ^^W3 P3,

• 3 = 1

где P3 — некоторое «простое» вероятностное распределение, задающее компоненту смеси, a Wj Е [0,1] — веса компонент, причем 321=1 ^wj — 1- Компоненты смеси часто называют кластерами. Случайный вектор X подчиняется модели смеси распределений, если он представим в виде

к

X — ^X jI {Т — j}, j=1

где X³ имеет распределение Р,, а случайна я величина Т равна номеру кластера, причем Р(Т = j ) = Wj. Кроме того, величины X ³ независимы с Т . Следующие утверждения можно найти в книге [10].

Утверждение 7. Обозначим EX3 = /,, DX3 = S, (в предположении что они существуют). Тогда математическое ожидание и матрица ковариаций по смеси распределений равны кк

EX = £ EX ³ Р(Т = j) = £ Wj /j .

3=1

DX = £ WjSj + £ W,/(/)T - £ WjW,/(„Щ. 3=1          3=1

Докажем утверждение. Первое равенство очевидно. Для вычисления матрицы ковариаций посчитаем матрицу нецентрированных вторых моментов

EXXT = E (£ X3I{Т = j}) (£ X3I{Т = j}| = £ EX3 (X3 )TI{Т = j} = 3=1                    3=13=1

= £ w, EX3 (X3 )T = £ Wj [EX3 (X3 )T - EX3 E(X3 )T] + £w, EX3 E(X3 )T = 3=1                   3 = 13=1

= £ Wj DX 3 + £ Wj EX 3 E(X3 )T = £w, S, + £ Wj / (/3)T. 3=1           3=1                    3=1j=1

Дисперсия получается по формуле DX = EXXT — EXEXT.

Утверждение 8. Представим вектор X в виде XT = (X£,X^'X^. Тогда условная вероятность кластера j при условии Xb равна г^з = Р(Т = j | Xb) =

W, pj^Xb) y*₌1W,p*(Xb) '

ГД ° P,^b) — плотность компоненты вектора Xb для расщгелелешія Р,.

Пусть также вектор X_a при условии вектора Xb и события Т = j имеет распределение (a|b)                                                                                                                                                                       (^a|b)

P, . Тогда вектор Xa при условии Xb имеет распределение смеси распределений Р, с весами й,

к

Mb)                (a|b)

^Р =2^^W3 ^Р3

3=1

.

Докажем утверждение. В доказательстве для простоты будем опускать верхние индексы. Первая формула следует из теоремы Байеса:

Wj, = Р(Т = j | Xb) =

Р(Т = j)p⁽,⁾(Xb |Т = j ) Е,^к=1 Р(Т = j )p,^b)(Xb | Т = j)

^W3 p(^b)(Xb⁾ Е(^к=1 W, p,^b)(Xb).

Вторую формулу получим с помощью условной плотности

p^(a№(xalxb )

Р^^Д^о'^ь) = E3=1y3^3aT^£aifb) p^(b)(^b)   "   E(^k=1 W, p,^b)Ob)

Ej =1 ^W j pj^WxV^M) Е^ 1 Wj р^Х)

= Е Wj p^w j=1

где pj"¹^ — условная плотность Х_а при ус-ловии Хь и события Т = j.

Поясним смысл утверждения. Пусть F — класс многомерных распределений, причем любой подвектор вектора Х имеет распределение из F. Предположим, что условное распределение одних компонент вектора Х при условии других компонент также лежит в F. Из утверждения еле дует, что если вектор Х имеет распределение, соответствующее смеси распределений из F, то аналогичные условные распределения также соответствуют смесям распределений из F. Иначе говоря, условное распределение компонент вектора из смеси нормальных распределений или распределений Стьюдента также имеет распределение смеси нормальных распределений или распределений Стьюдента соответственно.

4.2.    Смесь нормальных распределений

Плотность в модели смеси нормальных распределений имеет вид

к

р^(х) = ^L^Wj ч^(х \ р з . ^j )• j=i

Пусть Х1,...,Х_п — выборка из такой смеси распределений. Оценка параметров смеси производится решением задачи максимизации правдоподобия модели с помощью итерационного ЕМ-алгоритма [6], который заключается в выборе некоторого случайного начального приближения параметров и последующего чередования двух шагов. Для смеси нормальных распределений они имеют вид

Е-шаг. Вычислить некоторые вспомогательные величины

^W3 д^(ХМ. ^з )

^T = "к--------------- /V ^W sq^(Xi\pS. ^ s ) S=1

Смысл Tij — вероятность того, что объект Xi был пол учен из j-й компоненты смеси при текущем приближении параметров Wj, pj , ^j.

М-шаг. Вычислить новое приближение параметров

Wj =

1 ^п

1Еп ^

i=1

Tij,

п/ п pj = Ети х / i=1

п

^j = ^2 ^Tij ^(xi - ^pj ) i=1

/ п

∑︁ i=1

^Tij •

Критерий остановки. Итерации метода производятся до сходимости вариационной нижней оценки на логарифмическую функцию правдоподобия модели, которая в данном случае вычисляется по формуле п к                                  п к

^E(w,p. ^ ^,t) = ЕЕ Tij [ln W j +ln q(Xi\pj, ^j )] - EE Tij In Tij • i=1 j=1                                  i=1 j=1

Под сходимостью можно понимать, например, изменение Е не более чем на заранее заданное небольшое число е > 0 [6].

4.3.    Смесь распределений Стьюдента

Плотность в модели смеси многомерных распределений Стьюдента имеет вид к

р(ж) = 52 wj P(xI Р j, S j ,v), j=1

где p(xIpj , Sj, v ) — плотность многомерного распределения Стьюдента с v степенями свободы с центром в точке pj и матрицей масштаба Sj. Параметр v является гиперпараметром модели, то есть алгоритм не подбирает его значение.

Пусть X = (X1,...,X_n^ — выборка векторов из такой смеси распределений. Предлагаемый нами способ оценки параметров смеси заключается в выборе некоторого начального приближения на параметры и выполнения следующих шагов на каждой итерации.

Е-шаг. Выполнить несколько итераций следующих двух шагов:

• I.    Вычислить некоторые вспомогательные величины

^w j ^{q (X}i I ^pj , ^S j a-i /Ъ^ ) ^{r ij} = X                      ’

£ w_sq (Х- Ip_s , S_sai/bi )

S=1

Аналогично смеси нормальных распределений, величина r-j отвечает за вероятность того, что объект X- был пол учен из Дй компоненты смеси при текущем приближении параметров Wj, pj , Sj.

• II.    Вычислить

v + d          v 1                     -

• ^ai = 2 , ^bi = 2 ⁺ 2 ^^ ’ij ^(Х- - ^pj ) ^Sj ^(Х- - ^pj )’     ^С- = ^bi^,^^/a'^;^‘^,

j=i где d — размерность пространства, признаков. Величины q- ii bi имеют смысл параметров апостериорного гамма-распределения на. гамма-распределенные величины из определения распределения Стьюдента, при текущем приближении остальных параметров.

М-шаг. Вычислить новое приближение параметров

• п       / п,к                  п              / п                   1 п

• ^wj =          52 ’ij ’   pj = H^rij ^Ci ^Xi   ^LX^ ^Ci’   ^Sj = ^L^Ci ^(Xi-Pj ^)(Xi-Pj^)T •

i=1 / i,j=1               i=1          I i=1                     i=1

Критерий остановки. Итерации метода, производятся до сходимости функционала, который в данном случае вычисляется по формуле п к

^^(w’ Р’ ^S’^r,Q,b) = 52 52 ^г -1 i=i j=i

• -    2qz- [^{v + (X}i - ^pj^{)T S}j ^1(Xi - ^pj )] ⁺ 2 ln 2 - ^Г ( 2 ) ⁺ ( 2     1) WM - ^lnoi)j ^-

• п к              п

• ^-         ’ij In ’ij - y; [bi ln Qi - lnr(bi) + (bi - 1) Wbi) - In Qi) - bi] .

i=1 j=1             i=1

ln

wj

-

d.

- In 2т 2

-

- In det Sj

2           ³

-

С помощью приведенных итераций метод приближает локальный максимум логарифмической функции правдоподобия, вследствие чего возникает необходимость запуска процедуры несколько раз из разных начальных приближений. Подробнее сходимость метода обсуждается в разделе 5.

На основе максимизации величины £(w,p, E,T,a,b) можно подобрать гиперпараметр v следующим образом. Фиксируется сетка значений параметра v и для каждого ее значения производится несколько запусков алгоритма. Выбирается такое значение параметра, которое максимизирует E(w, ц, E, т, a, b).

5. Вывод формул оценки параметров смеси Стьюдента

Пусть X = (Xi,...,Xn) — выборка векторов из смеси распределений Стьюдента. Функция правдоподобия имеет вид п к

^L(w,P, ^у) = ПЕ Wjp(X-\pj, Ej,v ).

• -=i j=i

Семейство распределений не принадлежит экспоненциальному классу распределений, поэтому максимизировать такую величину проблематично. Воспользуемся представлением случайного вектора из распределения Стьюдента через нормальный случайный вектор и случайную величину из гамма-распределения. Далее введем скрытые (т.е. неизвестные) величины.

• 1)    Для каждого объекта Xi введем номер кластера в виде T- = (T-i, ...,T-k ) € {0,1}^к, причем ^к=1 T-j = 1- Вели чина T-j = 1 если объект Xi взят из кластера j и T-j = 0 иначе. Обозначим T = (Ti,..., T_n).

• 2)    Также для каждого объекта Xi введем случайную величину Ү, имеющую распределение r(v/2,v/2) таким образом, что справедливо представление

к

Xi = Е (^ + kj /^) і {Tij = 1}, j=i где случайный вектор ^-j имеет распределение JV(0, Ej). Обозначим Ү = (Yi, ...,Уп)

Вектор Xi имеет условное нормальное распределение JV(pj , Ej/у) при условии T-j = 1 и Ү = у. Совместное распределение векторов (X, T, Ү ) имеет плотность (по T это дискретная плотность)

p(x, t, y\w, ц, E, v) = П П [WjQ(^i\pj, EjJy-h (у- \ v/2, v/2)]^' . i=i j=i

Распишем логарифм этой плотности п к lnp(x,t,y\w,p, E,v) = ЕЕtij [ln Wj +lnq(x-\pj, Ej/у-) + lny(y-\v/2,v/2)] = i=i j=i п к

= ЕЕ tij i=i j=i

In Wj — 2 In 2л —

|lndet Ej + |ln yi —

^(xij ^{— p}j^{)T E}j ^i(xij ^{— p}j ) +

⁺1^ln I ^{— lnr(v/2) +} (I ^— 1) ^ln У і ^— 2yi] .

Оценка параметров смеси производится решением задачи максимизации функции правдоподобия модели с помощью ЕМ-алгоритма, в котором на Е-шаге оценка распределений величин Т и У вычисляется итерационно с помощью вариационного байесовского вывода. Вариационный вывод заключается в подборе приближения на апостериорное распределение (при условии X) величин Т и У в классе распределений, при которых Т и У являются условно независимыми. В итоге получается следующая итерационная схема:

• 1)    Выбор некоторого случайного начального приближения для значений Wj , qij , Ej. Векторы pj можно из иорма.тыюго распределения JV (0ДД. векторы Wj — из равномерного распределения на симплексе (распределение Дирихле). Матрицы Ej можно сгенерировать с помощью распределения Уишарта [14].

• 2)    Е-шаг:

• 1.    Выбор начального приближения распределения У.

• 2.    Вычисление приближения распределения Т при текущем приближении распределения У.

• 3.    Вычисление приближения распределения У при текущем приближении распределения Т.

• 4.    Повторять шаги b-с до сходимости.

• 3)    М-шаг.

• 4)    Повторять шаги Е и М до сходимости функционала L.

5.1.    Е-шаг. Внутренний шаг I.

На данном шаге вычисляется приближение распределения Т при условии X при текущих приближениях параметров по формуле ln r(t) к E₇ ln p(X, t,У |w,^, E,^), где математическое ожидание E₇ берется по текущему приближению распределения У, которое обновляется на шаге 2.

Замечание. Всюду под символом к будем понимать равенство с точностью до мультипликативной константы при рассмотрении вероятностей и равенство с точностью до аддитивной константы при рассмотрении логарифмов вероятностей.

Каждое Т имеет дискретное распределение со значениями во множестве бинарных векторов, в которых ровно одна единица. Для такого распределения логарифм плотности имеет вид ^^₌i tij ln r^j, г де r^j = P(Tj = 1) и ^j=1 rej = 1. Тогда чтобы найти распределение, нужно расписывать все rej с точностью до константы, которая не зависит от j.

ln r(t) к E₇ ln p(X, t, Уlw,p, E,v ) к

к

n k

^^ ^tej ln ^Wj - e=1 j=i

- lndet Ei —

2 ^j

^ (Xi — Pj )^TЕ^-1(Х_г — Pj )]

к

к

n k

^^ ^tej ln ^Wj ^— i=1 j=1

2lndet(E j /E₇T)

^— 2 ^{( X} e ^— ^j^{)T (E} j ^/Е 7 ^У е ) ^{1 ( X} e ^— ^j )]

к

n k к EEtij [ln Wj + ln Q (Xi ^j, Ej/Е7У )] .

e=1 j=1

Из полученного выражения следует, что оптимальное распределения Т (при условии X) таково, что величины rej к Wjq (Xe lpj, Ej/Е7Уе). Из условіія ^j=1 rej = 1 получаем приближение условного

Т1,...,Т_П независимы и

W₃ q (Xi lp₃ , Е₃ /Е 7 У ) ^rej = "", --------------------------------.

k

52 w_sq (Xe lp_s, E_s/E7Yi )

S=1

Величина Е7УІ вычисляется по текущему приб.тижеішто распределения Уе.

5.2.    Е-шаг. Внутренний шаг II.

На данном шаге вычисляется распределение на У при условии X при текущих приближениях параметров по формуле 1п у (у) к E_r 1n p(X, Т, y|w, р, У,н ), где математическое ожидание E_r берется по текущему приближению распределения Т.

Распишем это выражение с точностью до константы, которая не зависит от У, учитывая, ЧТО E^ . Tij = 1

1пу(У) = Er 1np(X, Т, y|w,p, У, v) к п к          г ,

= ЕЕ ErTij |1п у i=1 j=i

^— у ^(Xi - Mj ^{)Т y}j (^Xi ^{— p}j) ⁺ ( ₂^— 1 ) ^1п № - 2Уі] ^к

“ ^{Е Е} Ч( і=1 j =1

^— 1)^{1п Уі —} (^v + l^(Xi

^{— p}j^)ТУ- ^1(Xi ^{— p}j ) ) ^уі

п

∝

^п / ∑︁ _⎣

=

і =1

v + d 2

-

1п у і —

2 ⁺ 2 Е ^Tij ^(Xi^{— p}j^{)Т У}- ^1(Xi ^{— p}j ) j =1

Таким образом, получаем гамма-распределение с параметрами v 1 к bi =

v + d

^a = 2 ⁺ 2 Е ^Tij ^(Xi ^{— p}j^)ТУ- ^1(Xi^{— p}j ), j=1

Значения математических ожиданий обновляются по формулам Е7У =  "и

Е₇1пУ = ^(bi) — 1nQi, которые получены в разделе 2. Для краткости обозначим с = bi/ai.

5.3.    М-шаг.

На данном шаге обновляются значения параметров смеси посредством максимизации величины E_r,₇1np(X, Т, У |w, р, У, v), где математическое ожидание E_r,₇ берется по текущим приближениям распределений Т и У.

Оставляем только то, что зависит от Wj,pj , yj

Fx,v(w, m, У) = Er,71np(X, Т, У|w, m, У, v) к п к к ЕЕ E Tij 1п Wj i=1 j=1

-

- 1n det У, —

2 ^j

j(Xi —pj )^Т У ^{- 1} (Хі —pj ) Е 7Уі] =

п к

= ЕЕ ^Tij ^{1п W}j i=1 j=1

-

- 1n det У.;

2 j

-

2 ^(Xi ^{— p}j^)ТУ- ^{1 (X}i ^{— p}j )j .

Максимизация no Wj функционала Fx,^ (w,m, У) эквивалентна решению задачи

' п к

Е Е Tij 1п Wj —> max, i =1 j=1

к

E w₃ = 1, j=1

^Wj >  0.

Забудем на время про ограничения вида неравенства, составим функцию Лагранжа и найдем ее максимум п к                  ( к

0L

0wj

1 ⁿ

= — Е Tij

- А = 0,

^wj =

1 n

А Е i=1

^Tij •

Из условия ^^₌ i Wj = 1 получаем

^з =

n Ink

Е Ч ЕЕ

i=1 / i=1 s=1

^T is •

Заметим, что условия вида неравенства выполняются. Кроме того, найденное решение действительно является максимумом в силу выпуклости задачи.

Для максимизации по ц , приравняем производную к нулю

ЭҒх,р (w,m Е) _Е      v,

0ц,       = / > Tij Ci Ej (Xi Из) = 0, nn

У^ Tij CiXi = ^Tij СЩз , i=1

Ц =

n              In

Е Tij Ci Xi Е i=1         / i=1

Tij Ci.

Для максимизации no Ej приравняем к нулю производную по матрице Ej. Заметим, что по свойствам матриц справедливо

^{( X} i ^— Ц,^{)Т E} j ^{1 ( X} i ^— Ц, ) = t^r ^(^X i ^— Ц3^{)T E} j ^{1 ( X} i ^— Hj )) = t^r ^ ^E j ^{1 ( X} i ^— Hj^)(Xi - Ц3^)T ^ •

Пользуясь данным преобразованием, а также формулами матричной производной для

квадратных матриц [25]

X det X = det X • X dX

-Т

A_t,_Г(_А-^-1_Л) = - (_А- ^{- 1} ах ^-1)^Т.

О А

получаем

^ofx,p ^(w,m ^E) _ ¹ v^^Е    Г ⁰₁ , _v⁰ (y     A v- 1/'y       —

ОE₃      = 2 i=1 j=1 ^Tij  0E₃ ^{lndetE j + Ci} 0E₃^(Xi  ^^j ) ^E j ^{( X i}   ^^j )  =

1 n

= -₂ Е Tij (e, ^- - CiE^-1(Xi - ^j )(X i - ^j)^TE^-^ = 0.

Z i=1

Домножая на Ej слева и справа, получаем

n           n

TijEj = ^TijCi (Xi - Цз)(Xi - Цз)T, i=1          i=1

n

^Ej —     ^Tij ^Ci ^(Xi   ^ЦЗ ^)(Xi   ^ЦЗ )

i=1

/ n

∑︁ i=1

Tij •

5.4.    Вариационная нижняя оценка и сходимость метода

Итерации ЕМ-алгоритма продолжаются до сходимости вариационной нижней оценки [6] £(w, д, Е, г, a, b) = E_r,₇ ln р(Х, Т, Y |w, д, Е, v ) — E_r ln т(Т ) — E₇ ln7(Y).

Распишем каждое слагаемое отдельно

Er,7 lnр(Х, Т, Y|w, д, Е, v) = п к

= ЕЕ Er в, i=1 j=1

^(Xi ^{— д}з ^)ТЕ- ^{1(Х — д}з ^)E7 ^Yi ⁺ X ^ln X ^{— Г} ( х) ⁺ (9 ^— 1 ) E7 ^{ln Y}i ^— Д^Е7^Yi] = 2                          2  2\2/\2/         2

ln

Wj

—

2 ln 2тт + 2 E7 ln Y'i

—

• -    ln det Ез

2           ³

—

п к

= ЕЕ т., i=1 3 = 1

ln Wj

ln 2tt —

• -    ln det Е,— 2           ³

- 2aT [V + (Х. - д3)ТЕ3 1(Х. - д3)] + 2 ln 2 - Г ( 2 ) + ( 2     1) (-(M — ln ai)j , п к

Er ln т(Т) =         r.j ln r.j, i=1 j=1

п                п

E7 ln7(Y) = Е E7 ln7 (Yi) = Е [bi ln a. — lnГ(Ь.) + (b. — 1)E7 ln Y — aiE7Y] = i=1                i=1

п

= Е [bi ln ai — lnr(bi) + (bi — 1) (—(bi) — ln ai) — bi] . i=1

Изучим вопрос сходимости метода. Работа стандартного ЕМ-алгоритма основывается на формуле (см. [6])

log L(w, д, Е) = £(w, д, Е, q) + KL(q,pw,(1,^(t, уД— где q — некоторое распределение вектора (Т, Y), KL — дивергенция Кульбака-Лейблера. Для вариационной нижней оценки в этой формуле используется обозначение £(w,д, Е, q) в связи с рассмотрением произвольного распределения q вектора (Т, Y). С целью максимизации функции правдоподобия на каждом шаге максимизируется вариационная нижняя оценка, на Е-шаге — по q, на М-шаге — по параметрам w,д, Е. Тем самым ее значения не убывают. Максимизация на Е-шаге эквивалентна минимизации дивергенции по q, что эквивалентно выбору q = pw,p.,^(t, у|ж), при котором дивергенция в точности равна нулю. Тем самым вариационная нижняя оценка после Е-шага равна логарифму функции правдоподобия log L(w, д, Е), а значит, и функция правдоподобия тоже не убывает, сходясь к локальному максимуму.

Для рассматриваемой нами модификации ЕМ-алгоритма формула приобретает вид log L(w, д, Е) = £(w, д, Е, т, a, b) + KL(t х 7, p-m^^t, д|ж)).

Вариационный вывод на Е-шаге минимизирует дивергенцию. Но в рассматриваемом классе распределений, при котором распределения Т и Y условно независимы, равенство нулю дивергенции может не достигаться. Тем самым, нельзя гарантировать сходимость L к локальному максимуму. В рассматриваемых нами практических задачах естественно предположить, что распределения Т и Y близки к условно независимым, что должно обеспечивать хорошее приближение локального максимума с помощью получаемой оценки.

6.    Применение вероятностной модели

Модель смеси вероятностных распределений позволяет решать различные задачи машинного обучения, перечисленные во введении, получая согласованные результаты между ними. Рассмотрим каждую из них подробнее, предполагая модель смеси распределений, в которой плотность имеет вид к

р^(ж) =    W Р^(жІӨ3 )>

,=1

где Ө, — параметры распределения j-й компоненты смеси (например, вектор средних и матрица ковариаций).

6.1.    Кластеризация

Компоненты смеси можно рассматривать в качестве перекрывающихся кластеров. Каждый объект ж G R^ с некоторой вероятностью может быть отнесен к одному из кластеров. По утверждению 8 условная вероятность того, что объект ж соответствует кластеру j, равна р, (ж) =                .

£ wsр(ж|Өs)

s=1

Если wj , Ө ,

оценка величин w, ,Ө , соответственно, то в качестве оценки вероятности того, что объект ж соответствует кластеру j, можно использовать р,(ж) = Wjр(ж|Ө,) / 52 wsр(ж|Өs) . Данные оценки вероятностей можно рассматривать как s=1

степень уверенности метода при отнесении объекта ж к кластеру j. При проведении «жесткой» кластеризации, при которой объект ж необходимо строго отнести к одному из кластеров, выбираем кластер с максимальной вероятностью р , (ж):

j * = arg max р , (ж) = arg max w , р(ж|Ө,). j                      ,

6.2.    Аномальность

Объект ж G R^d считается аномальным, если значение плотности р(ж) меньше некоторого порогового значения q. Величина q выбирается как значение плотности р(ж), при котором вероятность получить объект с плотностью, не превосходящей q, в точности равна 0.05. Иначе говоря, величина q является решением уравнения

р(ж)1 {р(ж) 6 q}dж = 0.05.

R ^d

Описанная процедура определения аномальных объектов является частным случаем процедуры проверки статистических гипотез. В данном случае проверяется гипотеза о том, что объект ж является типичным, против альтернативы об аномальности объекта. Если плотность в точке ж меньше порогового значения q, гипотеза о типичности объекта отвергается в пользу альтернативы на уровне значимости 0.05. Данное правило является критерием для проверки гипотезы.

Можно также говорить о степени типичности объекта ж как вероятности получить объекты с плотностью, не меньшей плотности р(ж). Данная величина является аналогом р-value и вычисляется с помощью интеграла

р⁽у⁾і^{р⁽у) 6 р⁽ж^)}ау.

6.3.    Пропуски в данных

Оба рассмотренных выше метода работают только в случае, если в объекте х G R^d известны все значения, то есть отсутствуют пропуски. При наличии пропусков плотность объекта х можно оценить как интеграл плотности по подпространству пропущенных значений. Подробнее, пусть хк — вектор известных значений объекта, а х_и — все остальные значения объекта, которые пропущены. Тогда в качестве оценки плотности объекта хк рассматриваем

p(х)dхu,

Rdu где du — размерность вектора хи.

При рассмотрении смеси нормальных распределений или распределений Стьюдента эта плотность равна смеси маргинальных распределений, полученных в утверждениях 4 и 5.

6.4.    Условное распределение и вероятностная регрессия на признаки

Пусть объект х G R^d признан аномальным. Исследователь может выбрать элементы вектора х, которым он доверяет, а другие оценить через них. Без ограничения общности считаем, что х^т = (х^, х^) и значения хь являются доверяемыми. Кроме того, по причине наличия пропусков в данных, некоторые значения х_а могут быть неизвестны.

По утверждению 8 вектор х_а при условии значений хь имеет распределение смеси распределений с плотностью

к

Р(х) = ^ ^з р(х\Өз), j=1

где 0j — параметры распределения у-й компоненты смеси при условии значений хь- В случае смеси нормальных распределений параметры 0j для каждого кластера вычисляются по формулам из утверждения б, в случае смеси распределений Стьюдента — по формулам из теоремы 5.

Подставив вместо параметров их оценки, получаем оценку условного распределения вектора х_а, которое на практике является достаточно информативным показателем для принятия различных выводов о векторе х_а. В частности, из него можно получить

• •    Оценку математического ожидания Е(х_а \ хь) по утверждению 7. Эта оценка решает задачу регрессии признаков хь на при знаки х_а. Заметим, что задачу регрессии можно решать для разных признаков х_а и хь, используя только одну модель.

• •    Оценку дисперсии D(х_a \ хь) по утверждению 8.

• •    Оценку условных распределений кластеров всех объектов, у которых признаки Хь фиксированы и равны хь-

• •    Множества наибольшей плотности — множество значений х_а, для которых плотность по условному распределению больше, чем для остальных значений. Такое множество является аналогом доверительной области минимального объема. В одномерном случае таким множеством является интервал или набор интервалов.

• 7.    Моделирование PVT-свойств пластовых флюидов вероятностной моделью

  7.1.    Описание данных

7.2.    Смесь нормальных распределений

Существует ряд методов оценки представительности проб пластовых флюидов [16], таких как проверка герметичности пробоотборных камер, сопоставление давления насыще- ния нефти с давлением сепарации при температуре сепарации и др.; метод Хоффмана-Крампа-Хоккота, основанный на корреляции констант равновесия; определение представительности проб по критерию загрязненности технологическими жидкостями, применяемыми при бурении, перфорации и освоении скважины. В условиях же, когда имеются только сырые данные, выше представленные методы не могут быть применены, в связи с чем возникает необходимость в разработке алгоритмов выявления потенциально некорректных значений по сырым данным.

Для практического применения исследований PVT-свойств флюидов проанализирована база данных, содержащая результаты исследований более 3200 проб пластовых флюидов. Среди рассматриваемых признаков имеются следующие величины: пластовое давление, температура пласта, поверхностная плотность газа, поверхностная плотность нефти, га-зосодержание, давление насыщения, пластовая плотность нефти, объемный коэффициент нефти, вязкость пластовой нефти.

Задача предсказания PVT-свойств методами машинного обучения ранее рассматривалась в сильно ограниченном варианте. Например, в статьях [17], [18], [19] рассматривается предсказание давления насыщения через другие свойства с помощью искусственных нейронных сетей (ANN). В статьях [19], [20] аналогичным образом рассматриваются предсказания объемного коэффициента нефти. В статье [21] для предсказания упомянутых выше признаков используется SVM-регрессия.

В данной статье предлагается принципиально другой подход к решению этих задач, основой которого является введение вероятностной модели в пространстве свойств пластовых флюидов, в которой предполагается, что признаковое описание пробы получается независимо от всех остальных проб из некоторого вероятностного распределения.

Для описания данных сначала была применена смесь нормальных распределений из четырех компонент. Поскольку итерационная процедура ЕМ-алгоритма сходится к точке локального максимума логарифмической функции правдоподобия, метод запускался несколько раз из случайных начальных приближений. В качестве итоговой оценки берется оценка, полученная на итерации с наибольшим значением вариационной нижней оценки.

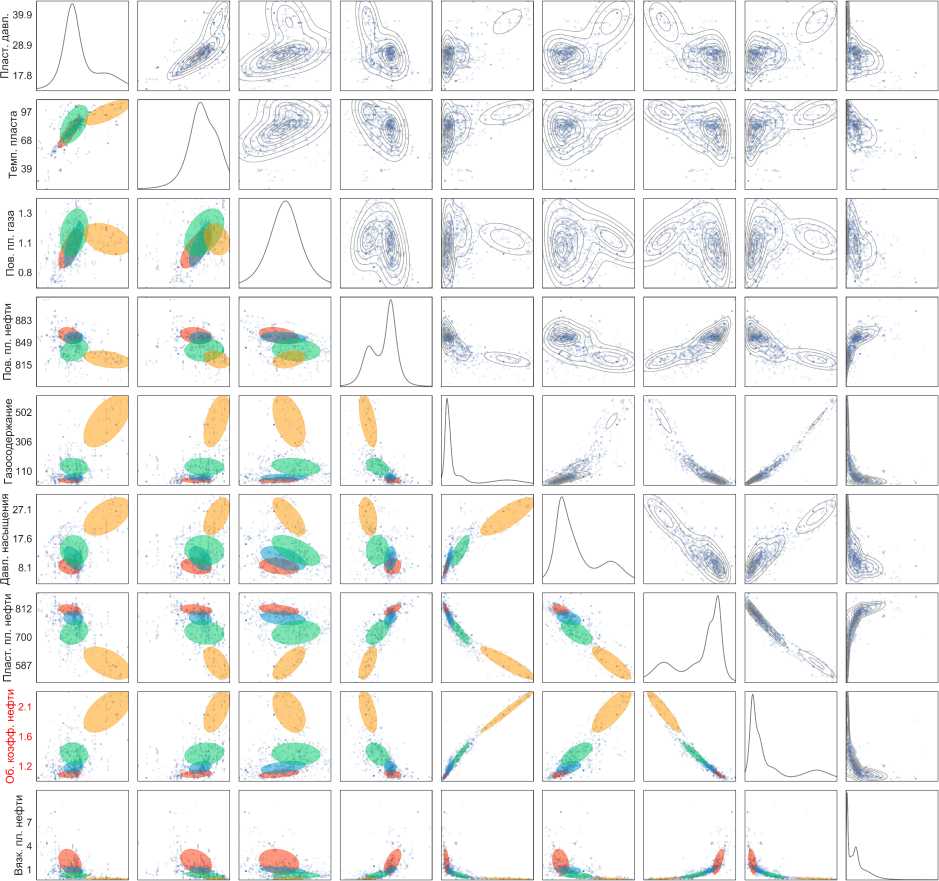
Результат оценки параметров приведен на рис. 1. На диагонали отображены плотности признаков по оцененной смеси. Каждая недиагональная клетка на графике соответствует проекции пространства признаков на все возможные координатные плоскости. Выше диагонали нарисованы линии уровня плотности полученной смеси распределений. Ниже диагонали эллипсами разных цветов отмечено взаимное расположение кластеров. Из графика видно, что серый полупрозрачный кластер накрывает два других кластера, что обусловлено наличием в данных шумовых объектов. Нормальное распределение обладает легкими хвостами, в следствии чего оценки его параметров не устойчивы к наличию в данных шумовых объектов. При построении модели смеси нормальных распределений по РУТ-данным ЕМ-алгоритм пытается с помощью трех кластеров описать основную часть данных, а с помощью четвертого — остальные менее типичные объекты.

Такое поведение алгоритма не соответствует целям решаемой задачи, поскольку модель данных должна хорошо описывать наиболее типичные объекты, и находить нетипичные, а не подстраиваться под них. Простое удаление серого кластера из модели смеси проблему не решает. Во-первых, серый кластер не накрывает красный, вследствие чего красный может быть смещен в сторону нетипичных значений, находящихся на удалении от серого. Полученная модель не сможет детектировать подобные нетипичные объекты. Во-вторых, серый кластер мог также описать некоторую часть типичных данных. При его удалении такие объекты будут признаны аномальными.

17.8 28.9 39.9      39   68   97     0.8   1.1   1.3      815 849 883      110 306 502     8.1 17.6 27.1     587 700 812     1.3   1.7   2.2     1    4    7

Пласт, давл. Темп, пласта Пов. пл. газа Пов. пл. нефти Газосодержание Давл. насыщения Пласт, пл. нефти Об. коэфф, нефти Вязк. пл. нефти

Рис. 1. Оценка параметров для смеси из четырех нормальных компонент в проекциях на двумерные и одномерные подпространства. Эллипсами разных цветов отмечено расположение кластеров. На диагонали отображены плотности признаков, выше диагонали нарисованы линии уровня плотности полученной смеси распределений

7.3.    Смесь распределений Стьюдента

Для устранения перечисленных выше недостатков к данным применена модель смеси распределений Стьюдента. Число степеней свободы / = 3 выбрано экспертно. На рис. 2 показана зависимость вариационной нижней оценки от итерации для наилучшего результата среди нескольких запусков из разных начальных приближений. Результат оценки параметров для четырех кластеров приведен на рис. 3. Синий и красный кластеры, полученные с помощью модели смеси многомерных распределений Стьюдента, соответствуют тем же кластерам в модели смеси многомерных нормальных распределений. Зеленый кластер разбивается на два, шумовой кластер отсутствует. Подобный результат является следствием устойчивости распределения Стьюдента к выбросам.

Центры кластеров приведены в табл. 1. При обучении кластеры определяются моделью с точностью до перестановки, поэтому порядок кластеров определен экспертно. Можно за- метить, что для большинства центры кластеров строго упорядочены по большинству признаков. Тип нефти, которому соответствует каждый кластер, также определен экспертно.

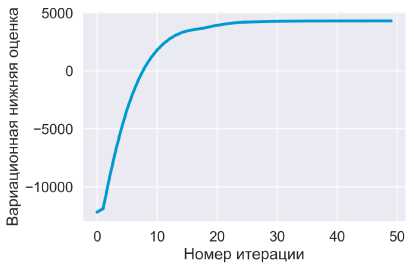
Рис. 2. График вариационной нижней оценки в зависимости от номера итерации

Таблица!

Центры кластеров, полученных с помощью модели распределений Стьюдента

	Кластер 0	Кластер 1	Кластер 2	Кластер 3
Доля проб	28.3%	27.7%	29.0%	15.0%
Пластовое давление, МПа	23.86	25.36	25.63	36.04
Температура пласта, ОС	75.33	80.47	83.91	96.12
Поверхн. плотность газа, кг/м3	1.01	1.07	1.17	1.11
Поверхн. плотность нефти, кг/м3	859.74	855.61	836.75	823.55
Газосодержание, м3/т	49.20	69.58	138.74	425.62
Давление насыщения, МПа	8.46	11.25	13.61	24.49
Пласт, плотность нефти, кг/м3	808.33	772.59	716.74	598.29
Объемный коэфф, нефти, м3/м3	1.12	1.20	1.36	2.04
Вязкость пласт, нефти, мПа • с	2.29 Тяжелая	1.24 Средняя	0.67	0.27 Особо
Тип нефти			Легкая
	и средняя			легкая

8.    Исследование модели

Поведение модели на основе смеси из четырех компонент распределений Стьюдента протестировано на искусственных данных, результаты экспериментов приведены далее. Кроме того, качество предсказаний модели протестировано на тестовых данных, не участвующих в обучении.

8.1.    Модельные эксперименты

В процессе исследования проанализированы результаты работы модели на искусственных пробах. Некоторые показатели проб фиксировались в трех различных вариантах эксперимента, их значения приведены в табл. 2. В каждом из трех рассматриваемых вариантов значения газосодержания менялись в пределах от 0 до 800 м3/т. Для каждого значения при помощи смеси распределений Стьюдента вычисляется вероятностная плотность пробы, вероятности принадлежности к каждому из трех кластеров, а также ожидаемые значения давления насыщения, пластовой плотности нефти, объемного коэффициента нефти. Все зафиксированные значения модель также использует для построения результатов.

Плотность пробы в зависимости от газосодержания для трех исследуемых вариантов показана на рис. 4. Черной пунктирной линией показан порог аномальности. Если плотность ниже порога, то проба считается аномальной. По графику видно, что в первом варианте типичным пробам соответствуют значения газосодержания от 90 до 190 м3/т, во втором варианте от 0 до ПО м3/т, в третьем от 0 до 90 м3/т.

17.8 28.9 39.9      39   68   97     0.8   1.1   1.3      815 849 883      110 306 502     8.1 17.6 27.1     587 700 812     1.2   1.6   2.1     1    4    7

Пласт, давл. Темп, пласта Пов. пл. газа Пов. пл. нефти Газосодержание Давл. насыщения Пласт, пл. нефти Об. коэфф, нефти Вязк. пл. нефти

Рис. 3. Оценка параметров для смеси из четырех компонент распределения Стьюдента в проекциях на двумерные и одномерные подпространства. Эллипсами разных цветов отмечено расположение кластеров. На диагонали отображены плотности признаков, выше диагонали нарисованы линии уровня плотности полученной смеси распределений

На рис. 5 для трех вариантов приведены оценки вероятностей того, что рассматриваемая проба соответствует каждому из трех кластеров проб. На основе этой вероятности происходит кластеризация. В проведенных экспериментах рассмотрен случай нежесткой кластеризации, при которой вероятности выступают в роли весов при дальнейших расчетах. Например, рассматривая первый вариант, можно сделать вывод, что проба в зависимости от значения газосодержания относится к синиму или зеленому кластеру.

На рис. 6 приведены графики предсказаний давления насыщения, пластовой плотности нефти и объемного коэффициента нефти в трех указанных выше вариантах при изменении газосодержания. Оранжевыми точками отмечены пробы, по которым происходило обучение метода. Закрашенной областью отмечен предсказательный интервал. Видно, что траектории предсказанных значений при изменении газосодержания являются гладкими, что следует из построения модели. Соотнося ширину построенных предсказательных интервалов с графиком плотности проб, можно видеть, что чем менее типична проба, тем больше неуверенность модели в предсказании значения, то есть интервал шире. Стоит также отметить, что наблюдаемое смещение предсказаний относительно общей массы точек объясняется тем, что в каждом варианте имеются зафиксированные признаки, которых нет на графиках. Если бы их не было, то предсказания выглядели бы как средние значения.

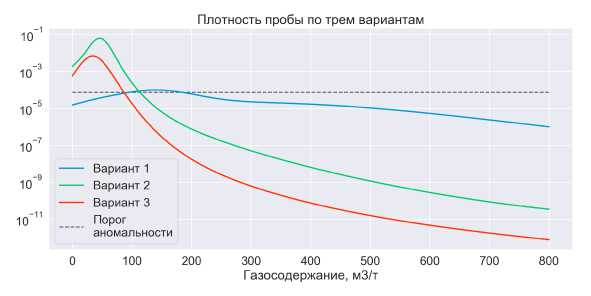
Рис. 4. Плотность пробы для трех вариантов в зависимости от газосодержания

Таблица2

Фиксированные значения признаков в модельных экспериментах

Признак	Вариант 1	Вариант 2	Вариант 3
Пластовое давление, МПа	35	25	18
Температура пласта, ОС	100	75	50
Поверхн. плотность газа, кг/м3	1.2	0.95	0.68
Поверхн. плотность нефти, кг/м3	800	845	880
Вязкость пластовой нефти, мПа • с	0.5	2	5
Газосодержание, м3/т	0 ... 800	0 ... 800	0 ... 800
Давление насыщения, МПа	?	?	?
Пласт, плотность нефти, кг/м3	?	?	?
Объемный коэфф, нефти, м3/м3	?	?	?

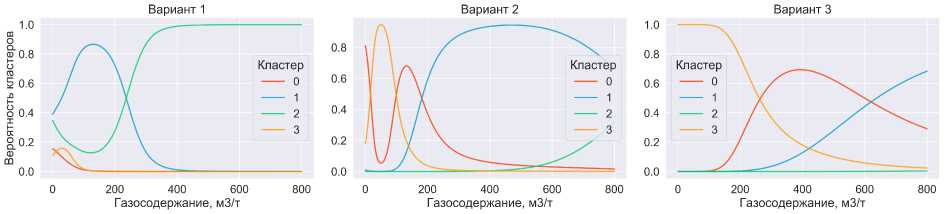
Рис. 5. Оценки вероятностей принадлежности пробы каждому из кластеров в зависимости от га зосодержания

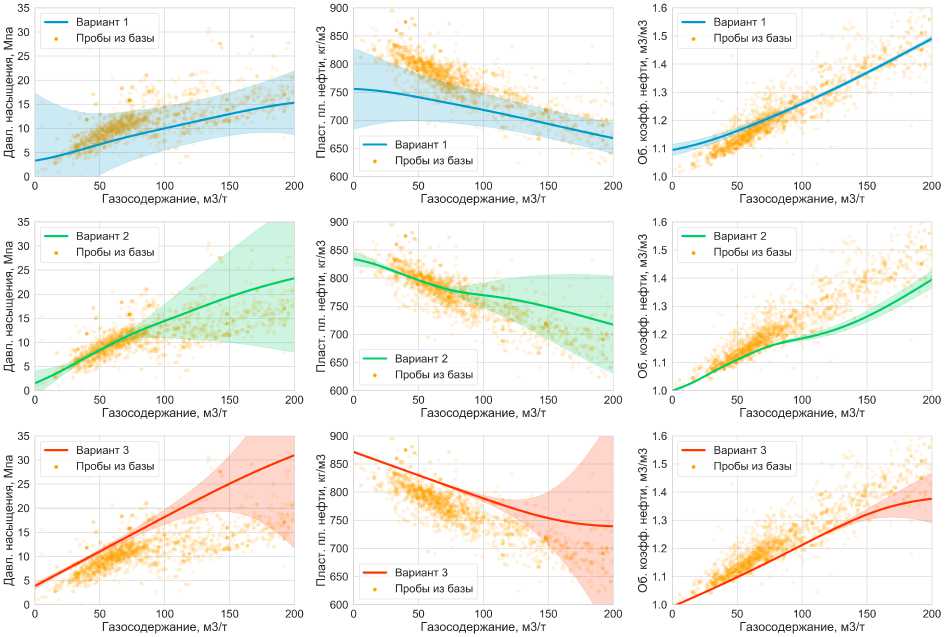
Рис. 6. Предсказания трех признаков в зависимости от газосодержания. Закрашенной областью отмечен предсказательный интервал

8.2.    Качество предсказания

Разработанная модель по введенной пробе вычисляет ожидаемые значения для неизвестных значений признака. Степень отклонения рассчитанных значений от истинных оценивается с помощью метрик качества. Пусть х_і — истинное значение признака, а оу — предсказанное в предположении, что само Х і неизвестно. Тогда относительной ошибкой предсказания Х і называется величина Сі = (х і — Хі )/хр показывающая, насколько велико отклонение предсказанного значения от истинного по отношению к самой величине истинного значения. Ошибки предсказания рассчитаны для тестового множества, содержащего порядка 650 проб, не участвующих при построении модели. При предсказании каждого значения модели передаются все известные значения пробы, кроме предсказываемого. Качество предсказания вычисляется как средняя абсолютная и среднеквадратичная ошибки в процентах, которые определяются как

МАРЕ = 122% £ |с |, n ^z—*

RMSPE = 100%

п

1Е

n ^

с

При расчете метрик среди набора чисел С і исключаются 2.5% наибольших и 2.5% наименьших значений по причине наличия выбросов и некорректных значений в исходных данных.

Для сравнения для каждого признака построены по 9 регрессионных моделей для следующих методов машиннного обучения — градиентный бустинг (XGBoost1, LGBM2, CatBoost3), а также sklearn-реализации4 случайного леса (RF), SVM-регрессии, нейрон- ной сети (ANN). Каждая такая модель обучена предсказывать один из признаков, рассматривая в качестве признакового описания все остальные признаки. Оптимальные гиперпараметры для каждой модели подобраны с помощью кросс-валидации на обучающем множестве. В табл. 3 и 4 приведены значения метрик МАРЕ и RMSPE для тестового набора данных. Видно, что в 5 из 9 случаев предсказание моделью смеси распределений Стьюдента оказывается точнее всех остальных моделей, а в остальных случаях не сильно отстает от них. Более того, эксперты обычно доверяют пластовому давлению и температуре пласта, которые точнее предсказывает градиентный бустинг, и поэтому их предсказание не настолько существенно в данной задаче.

Т а б л и ц а 3

Сравнение качества предсказания по метрике МАРЕ

	t-Mix	XGBoost	LGBM	CatBoost	RE	SVM	ANN
Пластовое давление	8.13	6.70	6.56	6.53	8.31	6.77	9.63
Температура пласта	5.96	5.50	5.67	5.75	5.78	6.58	6.25
Поверхн. плотность газа	3.42	6.21	6.20	7.08	6.23	4.30	7.38
Поверхн. плотность нефти	0.54	0.87	0.95	0.88	0.87	0.67	1.02
Г азосодержание	3.92	6.51	6.85	7.83	7.33	7.28	9.03
Давление насыщения	11.69	9.15	9.25	9.34	10.33	9.23	18.07
Пласт, плотность нефти	0.71	1.35	1.27	2.04	1.58	1.77	1.85
Объемный коэфф, нефти	0.68	1.43	1.57	2.70	2.13	2.23	2.62
Вязкость пласт, нефти	22.32	30.60	26.86	27.30	57.60	123.73	9.66

Т а б л и ц а 4

Сравнение качества предсказания по метрике RMSPE

	t-Mix	XGBoost	LGBM	CatBoost	RE	SVM	ANN
Пластовое давление	10.15	9.05	8.96	8.56	12.53	8.86	15.85
Температура пласта	7.50	7.15	7.26	7.15	7.61	8.23	7.93
Поверхн. плотность газа	4.75	7.80	7.79	8.72	7.95	5.44	9.38
Поверхн. плотность нефти	0.88	1.11	1.21	1.07	1.12	1.01	1.58
Г азосодержание	5.64	8.57	8.57	9.92	11.12	10.15	11.21
Давление насыщения	16.52	12.79	13.27	12.57	14.89	12.71	21.63
Пласт, плотность нефти	1.47	2.08	1.78	2.98	2.36	3.95	2.37
Объемный коэфф, нефти	1.49	2.12	2.36	3.74	3.34	4.03	3.29
Вязкость пласт, нефти	30.22	44.11	36.69	36.82	91.35	398.20	12.68

9.    Выводы

Предложенная в статье вероятностная модель смеси многомерных распределений Стьюдента для описания свойств PVT-проб имеет широкое практическое применение, среди которых проверка проб на аномальность, разбиение проб на четыре кластера, вычисление рекомендованных значений для пропущенных значений в пробе, а в случае аномальности пробы - для всех признаков, не выбранных в качестве доверяемых. Проведенные эксперименты показали, что получаемые рекомендованные значения не противоречат физическим свойствам PVT-проб, в частности обладают гладкостью по аргументам.

Разбиение проб на четыре кластера, в каждом из которых пробы имеют распределение Стьюдента, обосновано эмпирически сравнением со смесью многомерных нормальных распределений. В последнем случае качество получается неудовлетворительным по причине наличия шумовых объектов, на которые модель подстраивает отдельный кластер. Распределение Стьюдента имеет более тяжелые хвосты, благодаря чему меньше подстраивается под выбросы.

Вероятностная модель имеет существенные преимущества перед другими моделями благодаря тому, что при ее использовании удается решить сразу несколько задач, получая при этом согласованные между собой результаты. Рассматривая только задачу регрессии, в отличие от традиционного подхода к построению регрессионных моделей, вероятностная модель сразу позволяет получать как предсказания одного признака по другому признаку, так и наоборот, не требуя повторного обучения модели. В проведенных экспериментах качество полученного предсказания также превосходит другие модели.