Снижение нелинейных искажений под влиянием поляризационно-модовой дисперсии при передаче WDM-сигналов

В современных волоконно-оптических сетях связи ключевыми факторами, ограничивающими качество приёма сигналов, являются хроматическая дисперсия, нелинейности в волокне, шум волоконных усилителей и поляризационные эффекты, в частности, поляризационно-модовая дисперсия (ПМД). Традиционно нелинейные эффекты исследуют отдельно от поляризационных, а ПМД исследуют и моделируют в предположении линейности передачи. Однако в магистральных линиях связи большой протяжённости (сотни и тысячи километров) нелинейности и ПМД взаимодействуют таким образом, что их отдельное рассмотрение становится некорректным [1].

Для удовлетворения потребностей рынка в приложениях, передающих значительное количество мультимедиатраффика, операторы связи совершают переход от канальных скоростей 10 Гбит/с к скоростям 40 Гбит/с и выше. Сокращение длительности импульсов для повышения скорости передачи приводит к возрастанию влияния ПМД волокон на качество передачи сигнала. При этом становится критически необходимым рассматривать совместное влияние ПМД и керровских нелинейностей на качество принимаемого сигнала.

В ряде работ описано явление компрессии импульсов в результате воздействия ПМД на последовательность чирпированных импульсов [1, 2, 3]. Описанный эффект может проявляться независимо от природы чирпа: он может быть создан посредством модуляции лазера и в результате воздействия керровской нелинейности.

В работах [1, 3] описывается эффект увеличения открытия глаз-диаграммы в результате взаимодействия ПМД и чирпа, вызванного фазовой самомодуля-цией (ФСМ), по сравнению со случаем отсутствия ПМД. Известно, что в случае ФСМ максимальный чирп (по модулю) соответствует расположению фронтов нарастания и спада импульсов [4]. Указанный эффект имеет случайный характер и проявляется в реализациях волокна, обладающих высокой ПМД второго порядка. В чирпированном импульсе мгно- венная частота значительно меняется за время его прохождения. В свою очередь, высокая ПМД второго порядка вызывает существенное изменение направления вектора ПМД на сфере Пуанкаре при изменении частоты. В результате этого на протяжении импульса вектор поляризации сигнала изменяет своё положение относительно вектора ПМД, что означает изменение групповой скорости на протяжении импульса [1]. Таким образом, существует вероятность компрессии импульса, что будет выражено в увеличении открытия глаз-диаграммы и означает повышение качества сигнала вследствие взаимодействия ПМД и Керр-нелинейностей.

В случае передачи WDM-сигналов значительное влияние на чирп импульсов оказывает фазовая кроссмодуляция (ФКМ) [4], однако расположение экстремумов функции чирпа во временной области в общем случае не соответствует расположению фронтов.

При передаче WDM-сигнала керровские нелинейности приводят к возникновению кросс-поляризационной модуляции [5], т.е. зависимости поляризации сигнала на одной длине волны от поляризации сигнала на другой длине волны. При этом изменение поляризации зависит от амплитуды влияющих сигналов, то есть непосредственно от последовательности передаваемых бит при ООК-передаче [6]. Описанный эффект приводит к деполяризации сигналов. Так как воздействие ПМД на сигнал зависит от его поляризации, то каждый бит деполяризованного сигнала испытывает на себе уникальное влияние ПМД. Таким образом, при передаче WDM-сигнала взаимодействие ПМД и керровских нелинейностей приводит к возникновению сложного сочетания эффектов, результат которого, строго говоря, является случайным.

В свете вышесказанного актуальной задачей является детальное исследование взаимодействия ПМД и керровских нелинейностей в случае передачи WDM-сигналов. В данной работе будет рассмотрен эффект повышения качества передачи сигналов в результате такого взаимодействия и его зависимость от параметров передачи сигналов и характеристик среды передачи.

Описание применяемой модели

Полное аналитическое описание передачи WDM-сигнала в условиях воздействия ПМД, керровских нелинейностей и хроматической дисперсии не представляется возможным, поэтому в данной работе ис- пользуется численное моделирование.

Для моделирования нелинейной передачи оптических сигналов в волоконном волноводе широко применяются нелинейные уравнения Шрёдингера. Для учёта поляризационных эффектов должна применяться система связанных нелинейных уравнений Шрёдингера [4].

В данной работе рассматривается простейший случай WDM-передачи, когда одновременно осуществляется передача двух сигналов на различных длинах волн, при этом один сигнал рассматривается как исследуемый, а второй – как сигнал накачки.

В указанном случае система связанных нелинейных уравнений Шрёдингера принимает следующий вид:

dAlp. о dA». ie21 дЧ. dz ■’’ dt + 2 d11

a ,

⁺T A lp ^_

= iYl [| Alp |2 + 2| Amp |2 + 3 (I Aq |2 + I A |2 )) Alp

где l , m = 1;2, l ≠ m ; p , q = x , y , p ≠ q ; A lp ( z , t ) – соответствующий компонент огибающей сигнала; a - коэффициент затухания; β 1 , β 2 – первая и вторая производные постоянной распространения электрического поля; γ – коэффициент нелинейности.

Система (1) может быть численно решена Фурье-методом расщепления по физическим параметрам ( split-step Fourier method ) [4].

Уравнения (1) применимы для решения задачи распространения поля только в случае сегмента оптического волокна с определённым, неизменным по длине направлением осей двулучепреломления. Кроме того, величина двулучепреломления принимается постоянной на протяжении всего сегмента.

В то же время физическая природа ПМД подразумевает непрерывное изменение направления осей двулучепреломления и длины биений ПМД по длине линии. При этом изменения происходят на расстояниях порядка длины корреляции L_c [7].

Для корректного учёта такой особенности двулу-чепреломляющих волокон используется метод грубого шага ( coarse-step method ) [8]. При использовании данного метода всё волокно разбивается на сегменты, обычно одной длины, и принимается, что параметры двулучепреломления фиксированы в пределах одного сегмента волокна. Для этого сегмента численно решается система уравнений (1). Вращение вектора поляризации сигнала на сфере Пуанкаре имитируется применением матрицы поворота в каждом сегменте в соответствии с уравнением [8]:

A х ) _ f cos V sin V exp ( i ф )Y A x A y ^- sin V exp ( - i ф ) cos V J ( A y

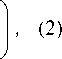
где A j – компоненты вектора Джонса огибающей сигнала, j = x , y ; ψ, φ – случайные величины, равномерно распределённые в диапазоне от 0 до 2π включительно.

Для удобства численного решения в качестве времени t будет подразумеваться «движущееся» нормированное время

_ t ^-Р 1 ср z ^T_ T , T ₀

где picp = (pix + piy)/2, T0 - длительность импульса. Тогда уравнения (1) запишутся в виде d-Ar+Apilp dz

^d A lp + i ^в 2 1 ^d 2 A lp d t 2 d t²

a ,

⁺ 2 A lp ^_

_ iYl f| Alp |2 + 2| Amp |2 + 3 (I Aq |2 + | Amq |2 )) Alp

где Apu p = p _{1 lp} - p _cp ; l принимает значения 1 или 2, p принимает значения x или y .

В реальных линиях связи двулучепреломление в волокне изменяется случайным образом как внутри строительной длины кабелей связи, так и для различных строительных длин. Закон распределения таких изменений для реального волокна может быть смоделирован только на основе измерений ПМД, протяжённых во времени, так как ПМД изменяется циклически в течение суток и в зависимости от погодных условий [9]. Поэтому в данной работе рассмотрение ограничивается моделью волокна с постоянным коэффициентом ПМД D p . Изменение ПМД во времени не рассматривается. Случайные изменения длины биений ПМД в волокне учитываются использованием параметра ∆β 1 / D p , распределённого нормально с математическим ожиданием 1/ 2 L_c , L c принимается равной 50 м.

Для исследования результатов взаимодействия ПМД и керровских нелинейностей моделируется волоконно-оптическая линия передачи, состоящая из пяти идентичных пролётов, каждый из которых включает в себя NZDSF-волокно длиной 80 км, волокно, компенсирующее дисперсию длиной 4,5 км, и EDFA-усилитель. Приёмник состоит из идеального полосового WDM-фильтра и квадратичного детектора. Для решения задачи распространения сигнала в каждом волокне применяется описанная выше модель.

Качество принимаемого сигнала оценивается посредством расчёта открытия глаз-диаграммы сигнала на выходе детектора по формуле

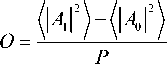
где A ₁, A ₀ – комплексные величины огибающих сигнала при передаче единицы и нуля соответственно; { ) - усреднение по всем битам соответствующего значения; P – пиковая мощность сигнала.

Для получения количественной оценки рассматриваемых эффектов рассчитывается зависимость открытия глаз-диаграммы от угла между исходными поляризациями исследуемого сигнала и накачки (угол θ) при за- данных мощностях и заданном коэффициенте Dp. При этом первоначально моделируется линия с учётом только нелинейных эффектов (т.е. Dp =0), а затем с учётом одновременного влияния ПМД и нелинейностей. Для получения статистической оценки имитационное моделирование повторяется многократно.

Сигнал накачки и исследуемый сигнал моделировались как случайная последовательность NRZ или RZ-импульсов, передаваемых со скоростью 40 Гбит/с в каждом канале.

Проведённые численные эксперименты показали, что добавление в усилителях аддитивного белого гауссовского шума не изменяет качественной картины, поэтому в приведённых ниже результатах шумом волоконных усилителей пренебрегается.

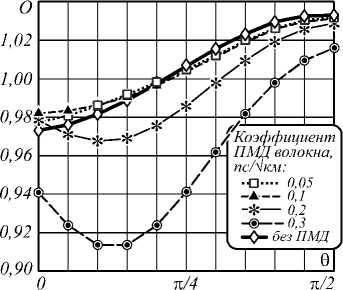
Рис. 3. Открытие глаз-диаграммы в зависимости от угла θ при передаче NRZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 40 мВт

Результаты моделирования

На рис. 1–3 приводятся результаты моделирования передачи двухканального WDM-сигнала с линейным кодированием NRZ по ВОЛП.

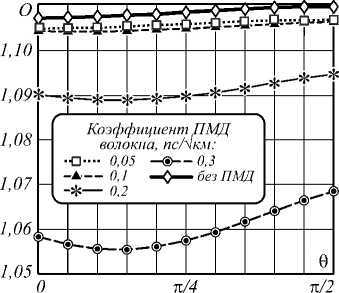
Рис. 1. Открытие глаз-диаграммы в зависимости от угла θ при передаче NRZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 5 мВт

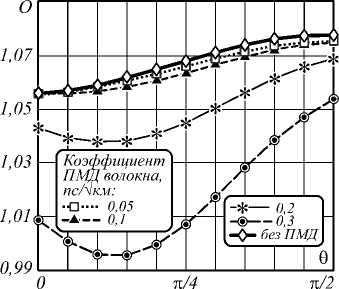
Рис. 2. Открытие глаз-диаграммы в зависимости от угла θ при передаче NRZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 20 мВт

Для всех графиков на рис. 1–6 зафиксированы значения случайных величин, определяющих изменение двулучепреломления в линии. Таким образом, при изменении коэффициента ПМД D p неизменной по длине линии остаётся функция, определяемая отношением ∆β 1 / D p . Также не изменяется направление осей двулучепреломления, то есть неизменны функции ψ( z ) и φ( z ), определяемые в уравнении (2).

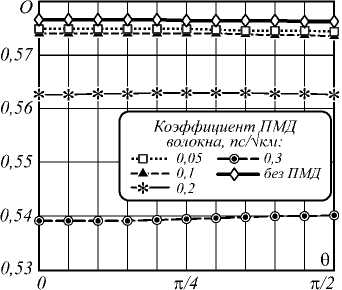
Рис. 4. Открытие глаз-диаграммы в зависимости от угла θ при передаче RZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 5 мВт

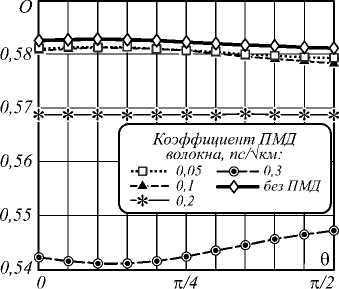
Рис. 5. Открытие глаз-диаграммы в зависимости от угла θ при передаче RZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 20 мВт

Из представленных результатов видно, что с увеличением мощности сигнала накачки проявляется эффект повышения открытия глаз-диаграммы в результате взаимодействия ПМД и керровских нелинейностей по сравнению со случаем отсутствия ПМД, то есть имеет место снижение нелинейных искажений. Связано это с тем, что повышение мощности накачки вызывает увеличение чирпа сигнала, вызванного ФКМ. Примечательно, что проявляется этот эффект при малых значениях угла θ, так как именно в этом случае чирп сигнала, вызванный ФКМ, будет наибольшим. Кроме того, деполяризация сигнала, вызванная ПМД, приводит к тому, что после нескольких длин корреляции угол между векторами поля двух WDM-сигналов будет существенно отличаться от исходного θ (в начале линии), поэтому нелинейные искажения, вызываемые ФКМ, будут снижаться при малых углах θ и повышаться при углах θ, близких к π/2, по сравнению со случаем отсутствия ПМД.

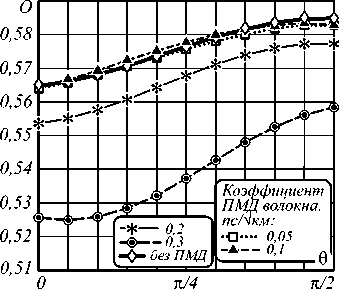
ждается сравнением значений открытия глаз-диа-граммы при отсутствии ПМД на рис. 1 –6).

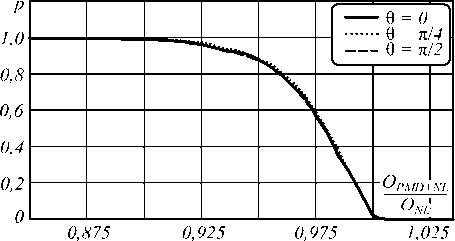
Рис. 6. Открытие глаз-диаграммы в зависимости от угла θ при передаче RZ-сигналов. Мощность исследуемого сигнала – 5 мВт, мощность сигнала накачки – 40 мВт

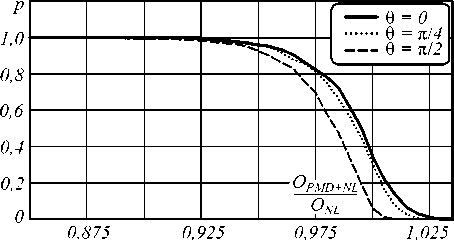
Рис. 7. Комплементарные интегральные функции распределения вероятностей значения открытия глаз-диаграммы в линиях с ПМД и нелинейностями (нормированного к значению, полученному для линии с нелинейностями, но без ПМД): NRZ-сигналы, мощность исследуемого сигнала – 5 мВт, накачки – 5 мВт (а); NRZ-сигналы, мощность исследуемого сигнала – 5 мВт, накачки – 40 мВт (б)

На рис. 4–6 приводятся результаты аналогичного моделирования при передаче сигнала с линейным кодированием RZ. Более низкое значение открытия глаз-диаграммы RZ-сигнала по сравнению с NRZ вызвано тем, что в обоих случаях используется одна и та же ширина полосы пропускания фильтра в приёмнике при различной ширине спектра двух сигналов.

Для RZ-сигналов сохраняются отмеченные выше закономерности, однако проявление эффекта снижения нелинейных искажений не так явно выражено, как для NRZ-сигналов той же мощности, и результат существенно меньше зависит от угла θ.

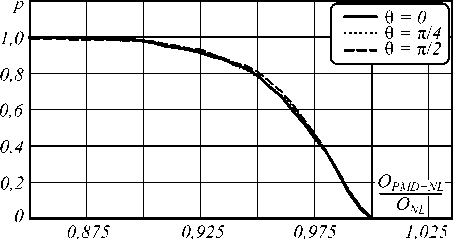
Для определения статистических характеристик взаимодействия нелинейных и поляризационных эффектов было проведено 5000 независимых вычислительных экспериментов, в каждом из которых рассчитывалась величина открытия глаз-диаграммы. При этом коэффициент ПМД волокна принимался равным 0,1 пс/√км. При тех же параметрах модели рассчитывалось открытие глаз-диаграммы при отсутствии ПМД (коэффициент ПМД принимался нулевым). На рис. 7,8 приводится комплементарная интегральная функция распределения вероятностей значения открытия глаз-диаграммы в линиях с ПМД и нелинейностями (нормированного к значению, соответствующему линии с нелинейностями без ПМД).

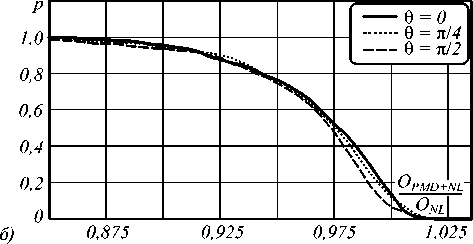
Рис. 8. Комплементарные интегральные функции распределения вероятностей значения открытия глаз-диаграммы в линиях с ПМД и нелинейностями (нормированного к значению, полученному для линии с нелинейностями, но без ПМД): RZ-сигналы, мощность исследуемого сигнала – 5 мВт, накачки – 5 мВт (а); RZ-сигналы, мощность исследуемого сигнала – 5 мВт, накачки – 40 мВт (б)

Из приведённых результатов следует, что вероятность снижения нелинейных искажений вследствие взаимодействия ПМД и керровских нелинейностей при передаче NRZ-сигналов существенно выше, чем в случае RZ-сигналов (в 2,6 раза при передаче сона-правленных сигналов и мощности накачки 40 мВт). Также при передаче RZ-сигналов не наблюдается существенной зависимости проявления эффекта от величины угла θ. Связано это с большей устойчивостью RZ-кода к нелинейным искажениям по сравнению с NRZ-кодом (различная устойчивость кодов подтвер-

Результат взаимодействия ПМД и нелинейностей имеет случайный характер и определяется ПМД данной реализации волокна. Частотные характеристики ПМД определяются ПМД второго и более высоких порядков .

Используя разложение вектора ПМД в ряд Тейлора в окрестности частоты несущей ω 0 , вектор ПМД второго порядка может быть представлен в виде [7]:

-    d-     .

^T _m=3- = ^T _m P ^{+ T} P ® , d ®

где т = т p - вектор ПМД; т - дифференциальная групповая задержка (ДГЗ); p ˆ – единичный вектор, направление которого определяет медленное принципиальное состояние поляризации [10]; индекс “ω” обозначает дифференцирование по частоте.

Зависимость τ и p ˆ от частоты для различных реализаций волокна определялась с помощью JME-анализа [11]. При этом для линий, в которых наблюдается эффект повышения открытия глаз-диаграммы в результате взаимодействия ПМД и нелинейностей, был обнаружен характерный признак, связанный с зависимостью ПМД от частоты. Так, на рис. 9 приведены зависимости τ ω (ω) для четырёх таких реализаций: функция меняет знак с отрицательного на положительный вблизи несущей частоты ω 0 . Для реализаций волокна, в которых не наблюдается эффект повышения открытия глаз-диаграммы, функция τ ω (ω) не обладает таким свойством.

Таким образом, значение ПМД второго порядка является определяющим фактором при проявлении эффекта снижения нелинейных искажений вследствие взаимодействия ПМД, ФСМ и ФКМ при передаче WDM-сигнала.

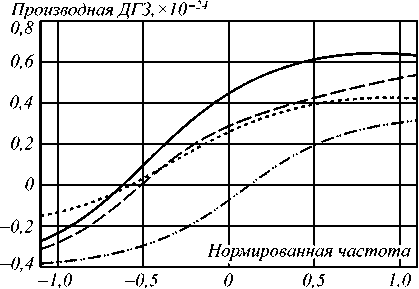
Рис. 9. Примеры зависимостей τω(ω)

Выводы

Полученные в работе результаты свидетельствуют о том, что влияние ПМД на полезный сигнал, подверженный искажениям вследствие ФСМ и ФКМ, может приводить к снижению этих искажений, что проявляется в компрессии передаваемых импульсов.

Показано, что описанный эффект более существенно проявляется при передаче NRZ-сигналов, чем в случае передачи RZ-сигналов. Вероятность проявления эффекта зависит от мощности сигнала накачки и угла между исходными векторами поляризации исследуемого сигнала и сигнала накачки.

Также в работе показано, что результат совместного воздействия нелинейных эффектов и ПМД на качество принимаемого сигнала определяется характером зависимости ПМД линии от частоты. Компрессия импульсов и, как следствие, снижение нелинейных искажений имеют место при смене знака производной ДГЗ по частоте с отрицательного на положительный вблизи несущей частоты сигнала.

Влияние ПМД на нелинейные эффекты и их взаимодействие обязательно должны приниматься во внимание при проектировании и модернизации (повышении бодовой скорости) волоконно-оптических линий передачи, в частности, при оценке вероятности превышения заданного порога ошибок. Высокое значение ПМД второго порядка во многих случаях снижает эффективность компенсации ПМД и является важным фактором деградации качества передачи сигналов, поэтому оценка качества принимаемого сигнала в таких случаях должна выполняться с учётом описанных в данной работе эффектов.

Исследование проводится при финансовой поддержке Министерства образования и науки Российской Федерации в рамках базовой части государственного задания образовательным организациям высшего образования №2014/240.