Снижение температурной напряженности в подшипниках скольжения с полимерными антифрикционными материалами

Невращающиеся втулки из полимерных материалов в условиях сухого и граничного трения быстро теряют свою работоспособность вследствие локализации напряжений, температуры и износа на небольшой части их поверхности трения.

Поиск различных способов улучшения работы металлополимерных пар привел к созданию принципиально новых видов трущихся сопряжений – «обратных пар» трения. В такой паре трения подшипник скольжения жестко закреплен на валу по своей внутренней поверхности, а его внешняя поверхность участвует в работе трения по опорной поверхности корпуса. В этом случае температура по всей внешней поверхности подшипника будет одинакова, так как она вся участвует в трении. При таком виде трения получаем осесимметричное температурное поле относительно оси вращения [6].

При рассмотрении конструкций узлов трения лесообрабатывающего оборудования было выявлено, что при использовании полимерного антифрикционного материала в обратной паре трения затрудняется отвод тепла с поверхности корпуса подшипника и поэтому потребуется искусственная вентиляция или отвод тепла через вал. Применение полимерной композиции с металлическим наполнителем позволит снизить температурное напряжение полимерной втулки в зоне трения [5].

Проанализируем стационарное плоское температурное поле подшипника скольжения из композиционного материала на основе полимера при внешнем радиусе цилиндрической стенки r ₂ и внутреннем r ₁ , с температурой поверхностей t_П и t ₁ соответственно. Принимаем, что для каждого заданного r X температура цилиндрической стенки не зависит от координаты z вдоль оси и угла φ и является функцией только радиуса стенки r X .

Рассмотрим конструкцию подшипника скольжения, когда антифрикционная втулка жестко закреплена на валу, а зона скольжения осуществляется между внешним диаметром втулки и корпусом подшипника (рис. 1). Из рисунка видно, что исследуемый антифрикционный материал на основе пластика с металлическим наполнителем длиной l ограничен снаружи цилиндрической поверхностью диаметром d 2 = 2 r ₂, а внутри -цилиндрической поверхностью вала диаметром d i = 2 r [2].

Для того чтобы определить температуру произвольно выбранной точки антифрикционного полимерного материала, определим ее как функцию расстояния r_X = d_X /2 от оси цилиндра. В качестве антифрикционного материала используется полимерный материал на основе полиамида с металлическим наполнителем в виде мелкой стружки низкоуглеродистой стали (Ст.0), которая обрабатывается магнитным полем в момент изготовления втулки для улучшения теплопроводности. Толщина стенки композиционной втулки составляет 3…5 мм. Коэффициент теплопроводности Л 2 Вт/(м ° С) полимерного материала с металлическим наполнителем рассчитывается в зависимости от объема металлического наполнителя и с учетом того, что теплоотдачей с торцов втулки можно пренебречь.

Зависимость теплопроводности полимерного вкладыша от степени наполнения металлической стружкой определяется по формуле для двухфазной системы [1], [4]:

Л = ^X a ⁺ 1, m ^{1 -} q в ₊ Л а (1)

• 3 Л в - Л а

где q a и Х а - объемная доля непрерывной фазы и обобщенная теплопроводность компонента А (полимера); q_B и Х в - объемная доля компонента В (наполнителя) и его теплопроводность.

Теплопроводность стали Х в = 40.. .50 Вт/(м ° С), а теплопроводность полимера находится в пределах Х а = 0,29 Вт/(м ° С). Принимая во внимание, что содержание металлического наполнителя не превышает 20 %, теплопроводность композиционного материала составит Х 2 = 0,4...0,7 Вт/(м ° С).

Для получения уравнения температурного поля в цилиндрической стенке воспользуемся уравнением Фурье, представленным в цилиндрических координатах [7]:

д t       д 2 t   1 д t    1 д 2 t    д 2 t_x

= а (     +     +       + ),      (2)

дт     д r 2 r д r r 2 дф 2  д z 1

Введем дополнительное обозначение d t

---= U .

dr

Тогда получим:

dU + ¹ U = 0. dr r

После разделения переменных и интегрирования получим:

ln U + ln r = ln C 1 или Ur = C 1 .

Подставляя в равенство введенную ранее замену U, получим:

где а - коэффициент температуропроводности, м²/с; t - температура, ° С; т - время, с; r , ф , z - координаты рассматриваемой точки по радиусу r , углу ф и вдоль оси z .

Так как рассматриваемый процесс является стационарным, а t = f ( r ), производные t по т , ф и z в уравнении (2) будут равны нулю. Учитывая, что t является функцией только r , вместо уравнения в частных производных (2) будем иметь обыкновенное дифференциальное уравнение:

dt                       dr

— r = C i; откуда dt = C — . dr                      r

После интегрирования имеем:

t = C 1 ln r + C ₂.

Для дальнейшего решения введем

относи-

тельную координату p = r / r ₂ в уравнение (7) и получим:

d ² 1 1 dt

--1--- dr 2 r dr

t = C 1 In p + C ₂.

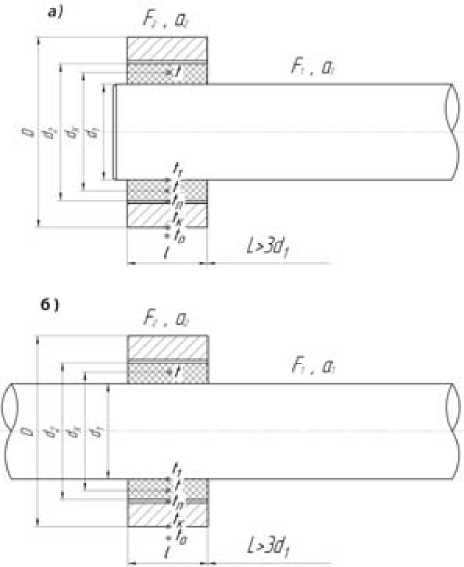
Рис. 1. Схема подшипникового узла (обратная пара): а - концевой подшипник; б - срединный подшипник

Для определения произвольных постоянных C ₁ и C ₂ воспользуемся граничными условиями первого рода, то есть когда на поверхностях цилиндра заданы температуры:

r при p = p 1: tr = r1 (p1 = —);

r r х при p = 1: tr = r2 (p2 = —).

r 2

На основании условий (9) и решения (8) получим:

t_n = С 1 lni + C ₂; откуда C ₂ = t_n ;       (10)

t i = C i ln p i + C ₂ или t i = C i ln p i + t_n .     (11)

Из последнего равенства (11) определим С 1 :

C i =

t i ^— t n ln p i

После подстановки значений С 1 (12) и С ₂ (10) в уравнение (8) получим следующее выражение для плоского осесимметричного температурного поля в подшипнике скольжения из композиционного материала на основе полимера.

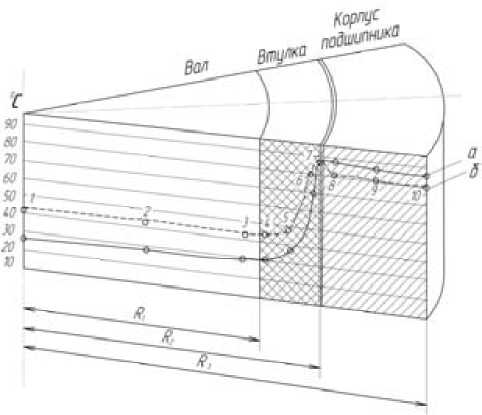
Рис. 2. Разрез подшипника скольжения с обратной парой трения:

а – полимер без металлического наполнителя (полиамид А6); б – полимер с металлическим наполнителем, обработанным магнитным полем (полиамид А6)

t - t n + ⁽ t i - t n ) -— — .             (13)

In — i

Для того чтобы найти t 1 - температуру на границе вала и слоя неметаллического антифрикционного материала при стационарном тепловом режиме – воспользуемся равенством теплового баланса [2]:

Q 2 - Q b

где Q ₂ - количество тепла, прошедшее через слой полимерной втулки с металлическим наполнителем, Вт; Q_e - количество тепла, отданное с поверхности вращающегося вала, Вт.

Количество тепла, прошедшее через слой полимерной втулки с металлическим наполнителем, находится как [3], [7]:

2 X 1 , X ^q 2 ^— —~(~" ⁽ tn - t i ) .

• ²   ln dl-

• d 1

Количество тепла, отданное с поверхности вращающегося вала, определяется следующим образом [2], [5]:

^Q e ^— — ^ ^ai^d i ^{X (} t i ^— t o ) ,             ⁽¹⁶⁾

Qb — n d 1 7 a i d 1 X 1 ( t i - t 0 ) ,             (16.1)

где t 0 - температура окружающего воздуха, ° С; a – коэффициент; теплоотдача с вращающегося вала в окружающую среду, Вт/м ° С. Численное значение a ₁ принимается по экспериментально найденному уравнению a ₁ — 15.6 • V 0,36 [1], [2].

Уравнение (16) используется для концевых подшипников, а уравнения (16.1) – для срединных, когда вылет вала в обе стороны от подшипника больше 3 d _i .

Подставляя выражения (15) и (16) в равенство (14), получим для срединного подшипника температуру на границе вала и слоя полимерного антифрикционного материала:

2 X 2 1 • t n + d 1 V a i d 1 X 1 ln d ² • 1 0

t '—----------------- ,________ d ¹     •            <‘7)

2 X 1 + d_x a dv X In d ²

’             d 1

Определив температуру в зоне контакта вала и втулки, далее определяем количество тепла, прошедшее через слой композиционной полимерной втулки с металлическим наполнителем, а затем количество тепла, отданное с поверхности вращающегося вала (рис. 2).

Из рис. 2 видно, что полимер с металлическим наполнителем способствует интенсивному отводу тепла из зоны трения за счет наполнителя, частицы которого выстраиваются в виде цепочек, по которым происходит дополнительный отвод тепла на вал подшипника скольжения.

Рассчитав температуру полимерного антифрикционного материала, можно сделать вывод об эффективности его применения в узлах трения лесообрабатывающего оборудования с особым режимом работы. Несомненно, обратная пара трения имеет больше преимуществ по сравнению с прямой парой, что в дальнейшем приведет к увеличению срока эксплуатации подшипника скольжения при снижении температурной напряженности в зоне контакта трущихся пар.