Снижение требований к размеру тестовой выборки биометрических данных при переходе к использованию многомерных корреляционных функционалов Байеса
Автор: Иванов Александр Иванович, Ложников Павел Сергеевич, Сулавко Алексей Евгеньевич, Серикова Юлия Игоревна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 2 т.15, 2017 года.
Бесплатный доступ
Рассмотрена проблема повышения надежности процедур биометрической аутентификации путем настройки сетей квадратичных форм и функционалов Байеса с использованием малой тестовой выборки. На малых тестовых выборках коэффициенты корреляции биометрических данных имеют значительную погрешность. Это препятствует их использованию при обучении (настройке) классических квадратичных форм и сетей Байеса. Показано, что многомерные корреляционные функционалы Байеса могут быть модифицированы под использование одинаково коррелированных по модулю биометрических данных. Предложено воспользоваться приемом симметризации корреляционных связей. Доказано, что в этом случае требования к объему биометрических данных существенно снижаются. Как следствие, настройка (обучение) квадратичных форм и сетей наибольшего правдоподобия Байеса становятся гораздо более устойчивыми задачами. Приведены графики, позволяющие оценить, насколько удается снизить размеры выборки биометрических данных.
Биометрическая идентификация, квадратичные формы, многомерные функционалы байеса, сети квадратичных форм, сети функционалов байеса
Короткий адрес: https://sciup.org/140191883
IDR: 140191883 | УДК: 519.24; | DOI: 10.18469/ikt.2017.15.2.12
Текст научной статьи Снижение требований к размеру тестовой выборки биометрических данных при переходе к использованию многомерных корреляционных функционалов Байеса
Одной из важнейших проблем современной науки и техники является проблема плохой обусловленности большинства вычислительных алгоритмов. Иногда эту проблему образно называют «проклятием размерности». Наиболее глубоко проблема «проклятия размерности» изучена применительно к задаче решения систем линейных уравнений или обращения матриц [1-2]. Введен и широко используется специальный параметр контроля «качества матрицы»: число обусловленности cond [А]. Параметр cond [А] может изменяться в пределах от 1 до и по своей сути является коэффициентом усиления погрешности исходных данных. При cond [А] = 1 погрешность исходных данных не усиливается, при cond [А] > 1 погрешность конечного результата увеличивается пропорционально числу обусловленности.
Обычно перед решением системы линейных уравнений И-л- = .у оценивают число обусловленности матрицы [ А ] и вектор ошибок входных данных - Ar . Это позволяет заранее оценить значение вектора ошибок конечного результата Ду = cond [а] • Дх .
Если результирующая погрешность Ду оказывается велика, существует два пути возможного ее понижения. Во-первых, можно снизить погрешность исходных данных за счет их накопления (увеличения объема выборки в k раз). Применив метод наименьших квадратов [3], можно снизить результирующую ошибку в 4к раз. Во-вторых, мы можем регуляризовать задачу по Тихонову [4], добившись необходимых значений вектора ошибок вычислений.
Следует отметить, что приведенные выше два пути повышения стабильности результатов матричных вычислений актуальны для любых вычислений. Любые вычисления можно улучшить, вводя избыточность (увеличивая выборку) или применив какой-либо метод регуляризации вычислений.
Особенно ярко все это видно при решении задач биометрической идентификации личности. Если при решении идти по пути классической линейной алгебры, то придется иметь дело с квадратичными формами и обращением корреляционных (ковариационных) матриц очень высокой размерности от 400 до 1000:
в' = (£(х) - xf [А]’1 (Е(х) - х), (1)
где Е^ х ) – математическое ожидание вектора контролируемых биометрических параметров в нормированной системе координат; [ R ]-1 – корреляционная матрица контролируемых биометрических параметров.
Поскольку по техническим причинам обращать корреляционные матрицы [R]-1 размерности более 8 не удается, приходится вместо квадратичных форм использовать искусственные нейронные сети. Применение искусственных нейронных сетей вместо классических квадратичных форм [5-7] следует рассматривать как один из методов топологической регуляризации нерешаемой задачи. Производится топологическая замена технически нерешаемой задачи обращения корреляционных матриц высокой размерности на независимое обучение 256 искусственных нейронов. Следует отметить, что обучение сети из 256 нейронов стандартным алгоритмом [8] обладает рекордной устойчивостью и имеет линейную вычислительную сложность. Стандартизован- ный алгоритм [8] абсолютно устойчив, так как не является итерационным (в нем исключен направленный итерационный поиск весовых коэффициентов нейронов). Фактически стандартный алгоритм обучения является полностью детерминированным, так как он однозначно вычисляет знаки и значения весовых коэффициентов нейронов, опираясь на знание вектора математических ожиданий биометрических параметров ЕСг) образа «Свой», вектора стандартных отклонений биометрических параметров <т(л-) образа «Свой», а также вектора стандартных отклонений образов «Чужие».
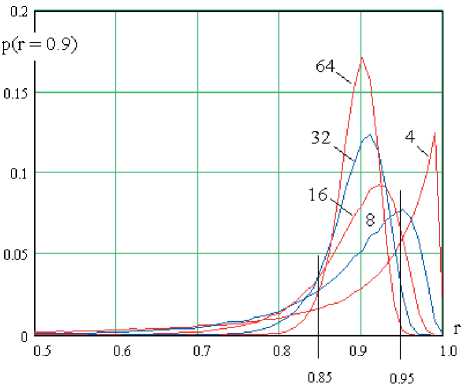
Рис. 1. Плотности распределения значений коэффициентов парной корреляции для сильно зависимых данных E ( r ) = 0,9 при n = 4, 8, 16, 32, 64
Проблема точного вычисления коэффициентов корреляции на малых выборках
Классический коэффициент парной корреляции двух биометрических параметров вычисляется по следующей формуле:
1 " г(.г1,х2) = -^ и ,=1
(ECrJ-Xj,.) <Е^х^-х,Х
С7{ХХ) СГ(Х2)
, (2)
где E (∙) – операция вычисления математического ожидания; ^С")— операция вычисления стандартного отклонения; n – размер выборки.
На малых выборках биометрических данных возникают значительные ошибки вычисления математических ожиданий АЕСг/), ЕЕ(х2) и стандартных отклонений До(л'/), ДбХх?). Совершенно так же, как и при решении систем линейных уравнений возникает эффект накопления ошибок. Оценить возможные значения ошибок вычисления коэффициентов парной корреляции можно по распределениям, приведенным на рис. 1.
Из рис. 1 видно, что при размере выборки n = 4 в значения коэффициента корреляции попадают в интервал от 0,85 до 0,95 с вероятностью 0,35. Однако если размер тестовой выборки увеличить до 8; 16; 32; 64, происходит рост вероятности попадания вычисляемых значений в заданный интервал до величин 0,59; 0,77; 0,89; 0,96.
Симметризация корреляционных связей как способ получения эквивалентной корреляционной матрицы с заведомо плохой обусловленностью
Известно [7; 9], что многомерные биометрические данные «Свой» всегда можно симметри-зовать, то есть заменить иными многомерными данными с той же самой энтропией. После симметризации корреляционная матрица биометрических данных вне диагонали будет иметь одинаковые коэффициенты парных корреляционных связей. Если биометрические данные сильно кор-релированы, то мы получим вне диагонали коэффициенты парной корреляции близкие к единице. Ситуация, когда все коэффициенты корреляционной матрицы вне диагонали близки к единице, приводит к очень плохой обусловленности матриц квадратичных форм. В частности, для данных, соответствующих рис. 1, пятимерная корреляционная матрица будет иметь большое число обусловленности:
тах(Я.) co»d[p] = —, . (5)
min(z;)
Как видно из выражения (4), собственные числа симметричной корреляционной матрицы (3) имеют одно большое значение ^ = 4,6 и четыре одинаково малые значения собственных чисел z2 — 4j = Я4 = A^ = 0,1. Симметричные корреляционные матрицы являются наихудшим вариантом для квадратичных форм (1), так как они не позволяют выделить и отбросить пару наиболее зависимых биометрических параметров.
Многомерные симметричные корреляционные функционалы Байеса
Полная симметрия корреляционных связей, являющаяся наихудшей для квадратичных форм, оказывается наилучшим соотношением данных для функционалов наибольшего правдоподобия Байеса [10, 11]. Следует отметить, что классический двухмерный коэффициент корреляции (2) по своей сути есть не что иное, как одна из форм записи правила Байеса:
p(x2 ,хх) • P^xx ) = Pfo /x2 ) • P^ ) . (6).
В этом легко убедиться, рассматривая предельные значения коэффициентов корреляции:
r(x,,x2)=I ^
P
= PU2 ) V P^xx /x2) = P(x2 fxx ) = 1;
0,9
cond 0,9
0,9
0,9
0,9 0,9
1 0,9
0,9 1
0,9 0,9
0,9 0,9
0,9 0,9
0,9 0,9
0,9 0,9
1 0,9
0,9 1
= 46; (3)
l\xx
, x2) = 0 =>
P
Для интервала корреляционных связей от 0,7 до 1,0 корреляционный вариант формулы Байеса можно записать следующим образом:
r^x2 , X, ) • P(xx) ® r(xx , x2) • P(x2) . (7)
4,6 ОД 0,1 0,1 0,1
Ошибки, возникающие при вычислении коэффициентов корреляции при попытках применения квадратичных форм (1), будут усиливаться примерно в 46 раз, что недопустимо для практики. Неприятности, порождаемые симметричными корреляционными матрицами, обусловлены тем, что число обусловленности определяется как отношение максимального и минимального собственных чисел ^i используемой матрицы
Приближение (7) становился точным равенством только при предельно высоких значениях коэффициентов парной корреляции. В принципе, можно построить некоторые корреляционные функции
F(r(xx,X2); P(x2^ ;
F2,xxY P
Одним из самых простых правил является использование равнокоррелированных биометрических параметров с суммированием близких значений, вычисленных на реальных данных ко-
эффициентов парной корреляции. В частности, может быть использован симметричный корреляционный функционал Байеса третьего порядка:
R(xx,x2,x3) =
r(xx, x2) + r(xY, x3) + r(x2, x3)
Решающее правило для такого функционала строится в виде правого и левого порога для его допустимых значений от min(T?(x1,x2,x3)) до maxf^XpXj.xJ). Определениенареальныхбио-метрических данных образа «Свой» допустимых порогов min(T?(x1,x2,x3)), max(T?(x1,x2,x3)) является настройкой (обучением) трехмерных решающих правил Байеса.
Очевидно, что по аналогии с трехмерным корреляционным функционалом Байеса может быть использован четырехмерный симметричный корреляционный функционал Байеса
R(xv,x2,x3,x^ =
r(xA , x2) + r(xx , x3) + r(xx, x4)
~ 6 + (9)
r(x2,x3) + r(x2,x4) r(x3,x4)
6 + 6 ■
В общем случае n -мерный симметричный корреляционный функционал Байеса имеет следующее формальное описание:
RU^X,,....^,,)^
-{r(x1,x2) + r(x],x2)+ ... +r(x1,x„) +
+ /'(x2,x3)+ ... +r(x2,x„) +
+ Г (x„_,, x„)} ■ ---—-----------------.
(n -1) + (» - 2) +... + (n - n)
Нетрудно заметить, что корреляционные функционалы Байеса третьего порядка построены на усреднении трех коэффициентов парной корреляции, каждый из которых имеет случайную ошибку, обусловленную малой выборкой биометрических данных [12]. Так как происходит усреднение трех коэффициентов парной корреляции, случайные составляющие ошибок каждого из частных коэффициентов корреляции ослабляются в V3 раз в значениях результирующего трехмерного корреляционного функционала (8).
Четырехмерный корреляционный функционал подавляет случайную составляющую в л/б раз. При применении n-мерного корреляци- онного функционала происходит подавление случайных составляющих ошибки примерно в ^n1 -n)/2 раз. С ростом размерности решающих правил мы наблюдаем почти линейный рост подавления случайных ошибок, возникающих из-за малого размера обучающей (тестовой) выборки.
Численный эксперимент по оценке эффекта подавления случайных погрешностей, вычисления коэффициентовпарныхкорреляции на малых выборках
Эффект подавления случайных составляющих погрешности с ростом размерности корреляционных функционалов Байеса можно оценить численным моделированием. Для этой цели необходимо использовать равнокоррелированные данные, получаемые умножением вектора псевдослучайных независимых чисел на симметричную связывающую матрицу [7; 9] с единичной диагональю и одинаковые элементы вне диагонали:
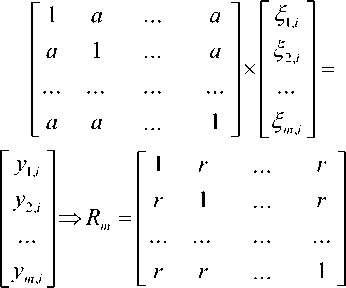
В итоге мы получаем выходные данные с близкими коэффициентами корреляции (см. рис. 2). Из рис. 2 видно, что по мере увеличения размерности корреляционных функционалов Байеса монотонно падает их стандартное отклонение, что приводит к росту вероятности попадания вычисленного функционала в интервал значений от 0,85 до 0,95. Так, для классического двухмерного коэффициента корреляции выборка из 16 примеров дает вероятность 0,77 попадания значений в заданный интервал. Переход к использованию четырехмерных корреляционных функционалов позволяет повысить вероятность попадания в интервал от 0,85 до 0,95 до величины 0,84. Это эквивалентно увеличению тестовой выборки с 16 до 24 примеров (рост объема выборки на 50%).
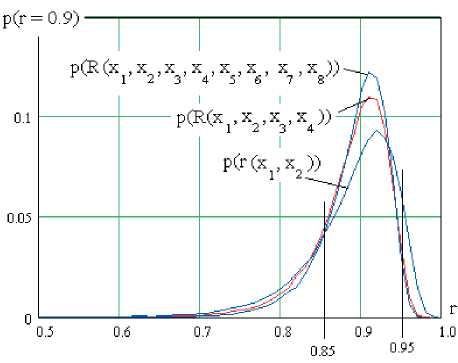
Рис. 2. Распределения значений классических двухмерных коэффициентов корреляции, а также четырехмерных и восьмимерных корреляционных функционалов Байеса, вычисленных на выборках из 16 примеров
Еще больший рост объема выборки будет наблюдаться при переходе от двухмерных коэффициентов корреляции к восьмимерным корреляционным функционалам. В этом случае в заданный интервал значения функционалов попадают с вероятностью 0,88, что эквивалентно росту обучающей выборки с 16 до 31 примера (рост объема выборки на 94%). При дальнейшем увеличении роста размерности вычисляемых корреляционных функционалов монотонно будет падать случайная составляющая погрешности вычислений. Это эквивалентно некоторой топологической регуляризации вычислений, осуществляемых сетями Байеса-Хэмминга [10-11].
Практически реализуемый алгоритм симметризации задачи многомерного корреляционного анализа Байеса
Изложенные выше теоретические обоснования многомерной корреляционной обработки биометрических данных приложим к конкретной технологии распознавания рукописных образов. Ориентация именно на технологию распознавания рукописных образов обусловлена тем, что наши данные может проверить любой желающий. Только для рукописных образов любой желающий может получить самостоятельно достоверные биометрические данные в любом требуемом объеме.
Для того чтобы это было возможно, в Лаборатории биометрических и нейросетевых технологий «АО Пензенского научно-исследовательского электротехнического института» для университетов России, Казахстана и Беларуси создан сво- бодно распространяемый программный продукт «БиоНейроАвтограф» [13]. Этот продукт анализирует 416 биометрических параметров почерка, являющихся некоторыми эквивалентами коэффициентов двухмерного преобразования Фурье от пары колебаний пера X(t), Y(t), возникающих во время воспроизведения человеком рукописных символов. Эти 416 параметров доступны для наблюдения, так как среда моделирования «БиоНейроАвтограф» [13] сохраняет их в файле «param.txt» после каждой инициации режима «проверить».
На рис. 3 дана гистограмма распределения значений 86 320 коэффициентов парной корреляции между 416 наблюдаемыми параметрами.
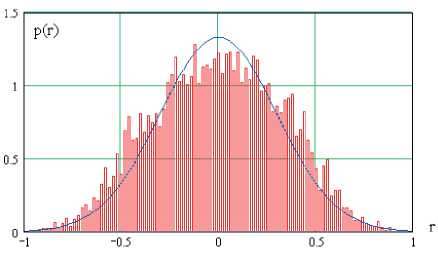
Рис. 3. Гистограмма распределения значений коэффициентов парной корреляции биометрических данных, порождаемых рукописным образом «Пенза»
Из рис. 3 видно, что гистограмма близка к нормальному закону распределения значений (сплошная тонкая линия). В рамках гипотезы нормальности распределения с нулевым математическим ожиданием и стандартным отклонением 67 = 0.34 в интервал значений от 0,85 до 0,95 коэффициенты корреляции попадают с вероятностью 0,005. Это означает, что мы можем обнаружить 430 высоких значений положительных коэффициентов корреляции и столько же отрицательных значений коэффициентов корреляции. Используя 860 значительных корреляционных связей, можно построить несколько сотен 32-мерных корреляционных функционалов Байеса [10-11].
Заключение
Если анализировать устойчивость процедур вычисления коэффициентов корреляции и вводить для них некоторый аналог числа обусловленности, то при тестовой выборке в 16 примеров биометрического образа мы получим некоторое условное значение cond (rCri,r2))i6. Если далее мы будем пользоваться двухмерными корреляционными функционалами Байеса, то мы получим некоторое решающее правило, дополня- ющее классические квадратичные формы и нейросетевые преобразователи [10-11]. Как следует из материалов данной статьи, увеличение размерности корреляционных функционалов Байеса эквивалентно формальному увеличению тестовой выборки.
Применение четырехмерных корреляционных функционалов Байеса эквивалентно увеличению на 50% размеров тестовой выборки. Этот эффект можно рассматривать как значительное снижение числа обусловленности (г(Х1,Х2))16 > cond(r(xi^2))24 или как значительное повышение устойчивости вычислений по отношению к случайным ошибкам, порождаемым малыми объемами тестовых выборок.
Отмеченный выше эффект повышения устойчивости вычислений наблюдается для любых биометрических данных, однако для получения этого эффекта необходимо использовать только одинаково коррелированные по модулю биометрические данные. Главное – это близость модулей коэффициентов корреляции. Многомерные корреляционные функционалы Байеса (10) легко могут быть модифицированы под использование одинаково коррелированных по модулю биометрических данных. Работа выполнена при финансовой поддержке РФФИ (грант № 16-07-01204)
Список литературы Снижение требований к размеру тестовой выборки биометрических данных при переходе к использованию многомерных корреляционных функционалов Байеса
- Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений. М.: Мир, 1969. -168 с.
- Райс Д. Матричные вычисления и математическое обеспечение. М.: Мир, 1984. -412 с.
- Лоусен Ч., Хенсон Р. Численное решение задач методом наименьших квадратов. М.: Наука, 1966. -230 с.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. -248 с.
- Качайкин Е.И., Иванов А.И. Идентификация авторства рукописных образов с использованием нейросетевого эмулятора квадратичных форм высокой размерности//Вопросы кибербезопасности. № 4(12), 2015. -С. 42-47.
- Волчихин В.И., Ахметов Б.Б., Иванов А.И. Быстрый алгоритм симметризации корреляционных связей биометрических данных высокой размерности//Известия высших учебных заведений. Поволжский регион. Технические науки. №1, 2016. -С. 3-7.
- Нейросетевая защита персональных биометрических данных. Под ред. Ю.К. Язова. М.: Радиотехника, 2012. -157 с.
- ГОСТ Р 52633.5-2011. Защита информации. Техника защиты информации. Автоматическое обучение нейросетевых преобразователей биометрия-код доступа.
- Aхметов Б.С., Надеев Д.Н., Фунтиков В.А., Иванов А.И., Малыгин А.Ю. Оценка рисков высоконадежной биометрии. Алматы: Изд-во КазНТУ им. К.И. Сатпаева, 2014. -108 с.
- Иванов А.И., Ложников П.С., Качайкин Е.И. Идентификация подлинности рукописных автографов сетями Байеса-Хэмминга и сетями квадратичных форм//Вопросы защиты информации. №2 (109)? 2015. -С. 28-34.
- Иванов А.И., Качайкин Е.И., Ложников П.С., Сулавко А.Е., Биометрическая идентификация рукописных образов с использованием корреляционного аналога правила Байеса//Вопросы защиты информации. №3 (110), 2015. -С.48-54.
- Волчихин В.И., Иванов А.И., Серикова Ю.И. Компенсация методических погрешностей вычисления стандартных отклонений и коэффициентов корреляции, возникающих из-за малого объема выборок//Известия высших учебных заведений. Поволжский регион. Технические науки. №1, 2016. -С. 45-49.
- Иванов А.И., Захаров О.С. Среда моделирования «БиоНейроАвтограф»//URL: http://пниэи.рф/activity/science/noc.htm (с 2009 г. для свободного использования вузами России, Белоруссии, Казахстана).


