Снижение трудоемкости эволюционного поиска со стохастической целевой функцией

Решение задачи комбинаторной оптимизации путем полного перебора возможных решений на практике зачастую оказывается неприемлемым, что обусловлено прежде всего значительной мощностью множества решений, трудоемкостью точного вычисления целевой функции на основе имитационно-аналитических моделей и временными затратами на получение статистических оценок качества решения. Современные приближенные алгоритмы комбинаторной оптимизации, в частности методы эволюционного поиска [1; 4], позволяют получать удовлетворительные решения за адекватное время, однако вопрос снижения их вычислительной трудоемкости для ряда прикладных задач стоит по-прежнему остро [3; 5; 9].

Сущность подхода

Предлагаемый подход рассмотрим применительно к генетическому алгоритму [1]. В случае стохастической целевой функции (что обусловлено имитационным аспектом моделирования исследуемого объекта [6; 8]) его наиболее трудоемким этапом является получение оценочной функции (так называемой фитнес-функции), требующее многократного вычисления значений целевой функции при помощи реализации имитационно-аналитической модели. Поэтому ключевым звеном, позволяющим обеспечить удовлетворительную для практических задач скорость сходимости алгоритма, является обоснование числа ее реализаци й при построении оценочной функции [1]. Коэффици-

78 в ыпуск 3/2019

ент вариации оценочной функции, зависящий от числа реализаций целевой функции, определяет не только ошибку ее оценки, но также результативность и скорость сходимости алгоритма, влияя на вероятность отбраковки «перспективных» решений. Поэтому существенно уменьшить вычислительную трудоемкость поиска возможно за счет более грубой оценки математического ожидания оценочной функции на начальных стадиях работы алгоритма, резко сокращая количество вычислений целевой функции, и более детальной на завершающих, обеспечивая точность результата [2; 7].

Таким образом, встает вопрос о снятии противоречия между трудоемкостью и точностью поиска путем обоснования переменного коэффициента V_n вариации оценочной функции. Для генетического алгоритма поиска конфигураций вычислительных структур в [1] он определен выражением

N

V n = V 0 - p ( V 0 - V 0, n

где n – номер «поколения» (итерации) генетического алгоритма; V ₀ – коэффициент вариации целевой функции; V _Δ – коэффициент вариации оценочной функции для последнего (с номером N_p ) поколения, определяющий точность решения.

При этом суммарное количество вычислений целевой функции в ходе поиска, выступающее мерой его трудоемкости, составляет

N p

T=z

n = 1

( V

к Vn J

.

Параметры алгоритма при этом подбираются исходя из максимизации показателя относительной результативности поиска

ψ=ϕPγ,

где φ – показатель средней относительной близости получаемого решения к оптимальному по значению оценочной функции; P _γ – вероятность «успеха» поиска, когда φ ≥ γ, где γ – априори заданная величина приемлемого отклонения.

Пример

Приведем результаты статистического исследования, демонстрирующие сравнительную эффективность предложенного подхода на примере выбора рациональных конфигураций перестраиваемой вычислительной системы [1]. В рассмотренном случае оценка общего количества формализуемых вариантов решений составляла около 4 ∙ 104, а заданное ограничение по трудоемкости поиска соответствовало Υ0 = 4,8 ∙ 105. Графики, иллюстрирующие пример зависимости показателя результативности поиска от его вычислительной трудоемкости, приведены на рисунке, где график «1» соответствует слепому поиску по методу Монте-Карло, «2»–«4» – традиционным процедурам генетического поиска с различной настройкой алгоритма, «5» – предложенному способу. Так, применение разработанного способа позволило отыскать квазиоптимальные решения, соответствующие с вероятностью 0,9 относительному значению целевой функции не менее 0,95 с выигрышем по времени около 8 раз (для 0,9 – около 12 раз).

Васильев А.С., Захаров И.В. Снижение трудоемкости эволюционного поиска...

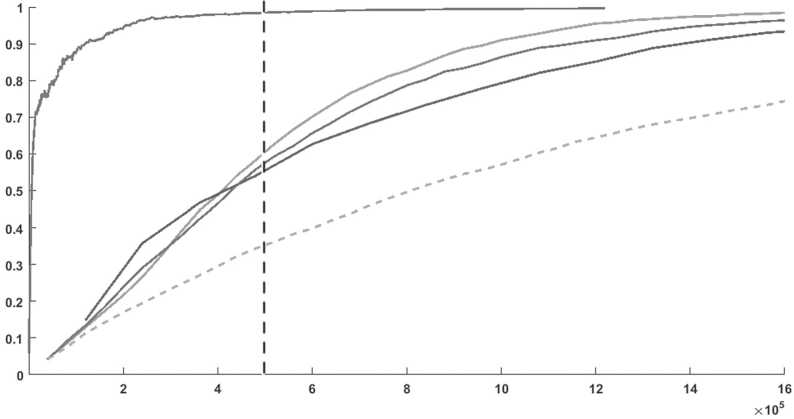
Пример зависимости показателя результативности поиска на базе генетического алгоритма от его вычислительной трудоемкости

Заключение

В литературе вопросы использования стохастической оценочной функции и изменения ее дисперсии в процессе работы генетического алгоритма в явном виде широко не рассматривались. Новизна предложенного подхода заключается в изменении количества вычислений целевой функции с ростом номера поколения, соответствующем снижению коэффициента вариации оценочной функции. Данный способ обеспечивает существенное снижение вычислительной трудоемкости эволюционного поиска, что позволяет расширить границы его эффективного использования в прикладных целях.