Снижение вероятности ложной тревоги в измерительном узле системы гидроакустического мониторинга

Вероятность ложной тревоги в измерительном узле системы гидроакустического мониторинга может быть снижена, если проводить первичную идентификацию источника сигнала. В связи с этим необходимо предусмотреть наличие в составе узла базы данных шумовых портретов морских целей, что может обеспечить безопасность мореплавания судов в условиях ограниченной видимости.

Для этого сигналы с выхода предварительного усилителя измерительного узла сравнивают с сигналами, хранящимися в базе данных, путем вычисления среднеквадратического отклонения. Определяют сигнал с минимальным отклонением и соответствующий ему источник. Сравнение сигналов может быть произведено и вычислением корреляционной функции.

Основная часть

Определение спектров сигналов

В соответствии с табл. 1 формируем вектора отсчетов времени и детерминированных сигналов. Ниже приведен фрагмент программы, вычисляющий вектор отсчетов детерминирован-– 569 – ного сигнала Y0b. Максимальное значение отсчета времени равно периоду нижней гармоники из табл. 1. Частота нижней гармоники (сигнал № 3) равна 2 Гц, а период соответственно 0.5 с. Частота дискретизации равна 4000 Гц.

t = 0:1/4000:0.5; % Формируем вектор времени с шагом 1/4000 с

Y0b = 5*cos(2*pi*10*t).*cos(2*pi*38*t)*0.2.*cos(2*pi*59*t); % Вектор сигнала

К полученному сигналу аддитивно добавим шум с амплитудой 2.5.

noise = 0.5*rand(1,length(t))-0.25; % Создаем шум с амплитудой 2.5

Y0b = Y0b+noise; % К сигналу аддитивно добавляем шум

Определим спектр сигнала, используя функцию расчета прямого быстрого преобразования Фурье:

Y0b = fft(Y0b,4000); % Находим БПФ сигнала

Y0b = Y0b.*conj(Y0b)/4000; % Находим модуль БПФ f = (0:1999); % Формируем вектор частоты с шагом 1 Гц

Сравнение спектров сигналов в Simulink

Для того чтобы сопоставить каждое значение модуля БПФ сигнала соответствующему значению частоты, необходимо сохранить массив отсчетов в виде матрицы размеров 2 на N (где N - количество отсчетов сигнала). В первой строке данной матрицы должны находиться дискретные значения частоты, а во второй – отсчеты модуля БПФ сигнала. Эта операция позволит выполнить моделирование сигнала как функции частоты в Simulink.

Y0b = [f; Y0b]; % Находим матрицу,

% состоящую из значений частоты и отсчетов save 'Y0b' Y0b % сохраняем найденную матрицу в файле simulink % Запускаем Simulink

Аналогично получаем матрицы размеров 2 на N для всех сигналов из табл. 1. Весь массив матриц Yib является содержимым базы данных шумовых портретов целей. Затем получаем матрицы размеров 2 на N зашумленных сигналов из табл. 1 повторно и формируется массив Yj. Каждая матрица из массива Yj сравнивается в Simulink с каждой матрицей из массива Yib путем вычисления среднеквадратического отклонения (рис. 1).

Результат моделирования работы блока первичной классификации приведен в табл. 2. Курсивом выделены минимальные отклонения принятого сигнала от эталонного.

Анализ данных табл. 2 показывает, что из 10 опытов пять дали неверный результат, т. е. вероятность ошибки идентификации равна 50 %. Для снижения вероятности ошибки необходима фильтрация сигнала.

Фильтрация сигнала

Выполняем аппроксимацию фильтра, используя программу Sptool. На рис. 2 показано окно этой программы с результатом аппроксимации рекурсивного фильтра десятого порядка, частота дискретизации (Fs) равна 4000 Гц, частота среза Fstop - 200 Гц.

Таблица 1. Детерминированные сигналы

Table 1. Deterministic signals

№№ п/п	Детерминированные сигналы
00	5*cos(2*pi*10*t)*cos(2*pi*38*t)*0.2*cos(2*pi*59*t)
11	sin(2*pi*5*t)
22	cos(2*pi*3*t)
33	sin(2*pi*2*t)* sin(2*pi*20*t)
44	sin(2*pi*4*t)* sin(2*pi*40*t)
55	cos(2*pi*6*t)* cos(2*pi*30*t)
66	cos(2*pi*7*t)* cos(2*pi*28*t)
77	sin(2*pi*5*t)* sin(2*pi*15*t)* sin(2*pi*30*t)
88	sin(2*pi*4*t)* cos(2*pi*24*t)* sin(2*pi*40*t)
99	cos(2*pi*3*t)*sin(2*pi*21*t)* sin(2*pi*63*t)

YO.mal

From File

YOb.mat

From File I

К Ts

Z-l

Discrete -Time Integrator

Display

Рис. 1. Сравнение матриц отсчетов зашумленных сигналов в Simulink

Fig. 1. Comparison of matrixes of samples of noisy signals in Simulink

Таблица 2. Результаты моделирования (шум с амплитудой 2.5). Сравнение спектров сигналов

Table 2. Simulation results (noise with an amplitude of 2.5). Comparison of signal spectra

Yib	Yj
	Y0	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9
Y0b	-2.718	112.9	88.22	22.82	60.00	52.43	48.77	0.91	12.48	6.33
Y1b	-6.4	-0.19	-29.52	-96.36	-56.45	-60.04	-61.35	-124.7	-109.4	-120.3
Y2b	-84.72	36.55	8.23	-61.70	7.10	-42.38	-40.99	-81.69	-71.57	-102.1
Y3b	-27.41	93.18	63.31	-31.37	42.28	28.76	19.57	-20.71	-13.42	-31.34
Y4b	-57.67	64.82	32.28	-41.03	23.08	-7.65	-11.4	-60.52	4.92	-64.71
Y5b	-56.31	54.39	43.80	-3.21	7.59	-5.41	-5.27	-53.51	-49.78	-57.78
Y6b	-47.61	58.98	47.73	-21.54	12.90	3.74	0.93	-49.64	-40.27	-55.17
Y7b	-7.761	117.8	82.95	12.36	60.42	44.10	44.11	-9.22	1.63	-14.88
Y8b	-10.54	110.3	77.06	15.08	63.07	50.92	43.97	-6.41	-52.85	-15.88
Y9b	5.44	116.8	105.57	27.33	65.33	54.65	56.09	6.78	16.05	-0.658

Для экспорта значений коэффициентов фильтра необходимо последовательно выбрать пункты меню (рис. 3):

Edit → Convert to Single Section, Targets → Generate C Header…

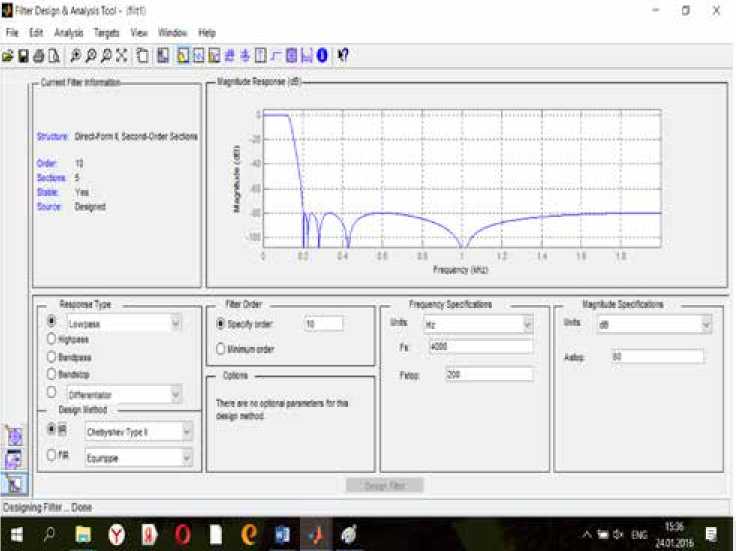
Рис. 2. Окно программы Sptool

Fig. 2. Sptool program window

Я Generate C Header

x

Vanat* name* n C header lie

Numerator ним

Denominator oen

Numerator length ml

Denomr-ator length dl

Data type to use in exsert

i) Export suggested

Double-precison ttoatmg-pont

[ owMel Oose Help

Рис. 3. Экспорт коэффициентов фильтра из программы Sptool

Fig. 3. Export filter coefficients from Sptool

Ниже приведены значения коэффициентов фильтра, экспортируемые из программы Sptool:

const int NL = 11;

const real64_T NUM[11] = {

0.0001230718046239,-0.0008771702296175, 0.002950005213996,-0.006248560520599, 0.009408767977326, -0.01071197455114, 0.009408767977326,-0.006248560520599, 0.002950005213996,-0.0008771702296175, 0.0001230718046239

};

const int DL = 11;

const real64_T DEN[11] = {

1, -8.567068149648, 33.11918306054, -76.07169564102, 114.952828427, -119.396787241, 86.31583589917, -42.88219550398, 14.01005883948, -2.71788355467, 0.2377241181237

};

Выполним фильтрацию сигналов в Simulink и сформируем массивы матриц размеров 2 на N Yibf и Yjf (рис. 4).

Ниже приведен исходный код программы цифрового фильтра на языке программирования С. Фильтр реализован на микроконтроллере dsPIC33FJ32MC204. Входные отсчеты x[0] предварительно сохраняются в буферном ЗУ АЦП в регистре ADC1BUF0.

/*Цифровой ФНЧ: рекурсивный, порядок 10, аппроксимация Чебышева II, частота дискретизации 4000 Гц, частота среза 200 Гц*/

//Подключение заголовочных файлов

#include

#include

#include

#include “signal.h”

#include

#include

//Настройка системы тактирования

_FOSCSEL(0x02);//Главный генератор без PLL

_FOSC(0xE2);//Режим HS int r;

Рис. 4. Фильтрация сигнала в Simulink

Fig. 4. Signal filtering in Simulink

//Массивы коэффициентов фильтра

#define NCoef 10

float y[0];

float ACoef[NCoef+1] = {

0.0001230718046239,

-0.0008771702296175,

0.002950005213996,

-0.006248560520599,

0.009408767977326,

-0.01071197455114,

0.009408767977326,

-0.006248560520599,

0.002950005213996,

-0.0008771702296175,

0.0001230718046239

};

float BCoef[NCoef+1] = {

1, -8.567068149648,

33.11918306054,

-76.07169564102,

114.952828427,

-119.396787241,

86.31583589917,

-42.88219550398,

14.01005883948,

-2.71788355467,

0.2377241181237

};

//Функция вычисления очередного выходного отсчета y[0] float iir(ADC1BUF0) { static float y[NCoef+1]; //Выходные отсчеты static float x[NCoef+1]; //Входные отсчеты int n;

//Сдвиг предыдущих входных и выходных отсчетов for(n = NCoef; n>0; n--) {

x[n] = x[n-1];

y[n] = y[n-1];

}

//Вычисление очередного выходного отсчета

x[0] = ADC1BUF0;

y[0] = ACoef[0] * x[0];

for(n = 1; n< = NCoef; n++)

y[0] + = ACoef[n] * x[n] – BCoef[n] * y[n];

PORTB = y[0];

return y[0];

}

//Функция задержки void delay() { int counter = 0;

for (counter = 0; counter<2; counter++) {

;

}

}

//Главная функция void main(void)

{

//Инициализация портов

TRISA = 0x0000;

PORTA = 0x0000;

LATA = 0x0000;

TRISB = 0x0000;

PORTB = 0x0000;

LATB = 0x0000;

TRISC = 0x0000;

PORTC = 0x0000;

LATC = 0x0000;

//Конфигурирование АЦП

TRISC = 0x0001; //RC0-цифровой вход

TRISB = 0x0000; //portB на выход

ADPCFG = 0xFFBF; //RC0(AN6)- аналоговый вход

AD1CON1 = 0x0000;

AD1CHS0 = 0x0006; //Подключение AN6 к УВХ

AD1CSSL = 0;

AD1CON1bits.SAMP = 0; //Начало преобразования while (!AD1CON1bits.DONE); //Преобразование завершено?

PORTB = iir(ADC1BUF0);

} //

}

Результаты повторного сравнения уже отфильтрованных сигналов представлены в табл. 3. Анализ табл. 3 показывает, что из 10 опытов уже только три дали неверный результат, то есть вероятность ошибки идентификации равна 30 %.

Таблица 3. Результаты моделирования (шум с амплитудой 2.5). Сравнение спектров отфильтрованных сигналов

Table 3. Simulation results (noise with an amplitude of 2.5). Comparison of the spectra of the filtered signals

Yibf	Yjf
	Y0f	Y1f	Y2f	Y3f	Y4f	Y5f	Y6f	Y7f	Y8f	Y9f
Y0bf	-2.718	112.9	88.22	22.82	60.00	52.43	48.77	-9.22	12.48	6.33
Y1bf	-6.4	-0.19	-29.52	-96.36	-56.45	-60.04	-61.35	-124.7	-109.4	-120.3
Y2bf	-84.72	36.55	8.23	-61.70	-23.08	-42.38	-40.99	-81.69	-71.57	-102.1
Y3bf	-27.41	93.18	63.31	-31.37	42.28	28.76	19.57	-20.71	-13.42	-31.34
Y4bf	-57.67	64.82	32.28	-41.03	7.10	-7.65	-11.4	-60.52	4.92	-64.71
Y5bf	-56.31	54.39	43.80	-3.21	7.59	-5.41	-5.27	-53.51	-49.78	-57.78
Y6bf	-47.61	58.98	47.73	-21.54	12.90	3.74	0.93	-49.64	-40.27	-55.17
Y7bf	-7.761	117.8	82.95	12.36	60.42	44.10	44.11	0.91	1.63	-14.88
Y8bf	-10.54	110.3	77.06	15.08	63.07	50.92	43.97	-6.41	-52.85	-15.88
Y9bf	5.44	116.8	105.57	27.33	65.33	54.65	56.09	6.78	16.05	-0.658

Заключение

В случае высокого уровня помехи необходима предварительная фильтрация сигнала, которая существенно снижает вероятность ошибки классификации. В измерительном узле системы гидроакустического мониторинга задачи цифровой обработки сигнала (цифровая фильтрация и спектральный анализ) реализуются на микроконтроллере, а для хранения массива матриц Yibf используется микросхема FlashROM.