Снижение виброактивности исполнительных механизмов систем управления техническими средствами

Одной из важнейших проблем промышленности и транспорта является необходимость постоянного снижения уровня вибрации и шума работающего оборудования.

Концерн «Аврора» является одной из ведущих фирм России по созданию высоконадёжных малошумных устройств гидроавтоматики, в том числе:

• -    СУ теплоэнергетическими установками;

• -    СУ рулевыми приводами;

• -    систем успокоения качки;

• -    СУ объектами с динамическими принципами поддержания и др.

Разработанные конструкции могут обеспечивать работу в различных климатических зонах и в широком диапазоне условий эксплуатации .

Исследования, опытная и макетная отработка новых технических решений, испытания и контроль серийных образцов аппаратуры производится на специализированных стендовых установках, которые являются уникальными техническими комплексами и позволяют выполнять опытно-конструкторские работы по созда- нию устройств гидроавтоматики различного функционального назначения [1].

Основными конструктивными методами уменьшения виброшумоизлучения являются методы дробления потока рабочей среды, многоступенчатого дросселирования с оптимальным выбором профиля рабочей зоны, агрегатирование исполнительной части систем управления .

Для того чтобы существенно улучшить виброакустические характеристики (ВАХ) гидроприборов, необходимо искать причины вызывающие шум и вибрацию или снизить виброактивность их источников. Этого можно добиться, если учитывать необходимость малошумности прибора ещё на стадии его проектирования. Поэтому весьма актуально введение принципа ма-лошумности в методику расчёта гидроприборов и оценки качества проектирования, исходя из условий минимальности уровней шумов. Основываясь на нём можно выбрать безкавитационный режим работы прибора, рассчитать его проточную часть, её профиль, ожидаемые уровни вибрации и гидродинамического шума (ГДШ).

При проектирование малошумных гидравлических приборов необходимо:

• -    исключать явления кавитации в проточной части;

• -    минимизировать влияние турбулентности потока;

• -    исключать образование крупномасштабных вихрей, возбуждающих низкочастотную вибрацию;

• -    снизить влияние волновых процессов при нестандартных режимах работы.

Физическая сущность возникновения кавитации при дросселировании жидкости в гидравлических устройствах СУ ТС определяется развитием каверн в зоне пониженного статического давления высокоскоростной струи жидкости. В критериальной форме развитие кавитации в проточной части представлено в виде

K ^{P сл P нп} , (1) pv ²

где: Р сл – давление за элементом дросселирования; Р нп – давление насыщенных паров жидкости;

• -    скорость жидкости в струе.

Из определения (1) следует, что критическое число кавитации К кр =1, т.е. при К<1 кавитация усиливается, а при К>1 – уменьшается.

В общем случае гидравлическое устройство содержит нерегулируемые местные и распределенные по длине сопротивления, образуемые поворотами, проточками и каналами, а также регулируемые сопротивления дросселирующих элементов типа шток-седло, золотник-гильза.

Обобщенное представление гидравлической характеристики Q ( h ) и критерий кавитации (1) позволяют определить области потока, где существует кавитация.

Используя уравнение Бернулли, получим, что эффективное регулирование расхода возможно, если при любом заданном ходе h регулирующего элемента выполняется условие p k(h) k1

2 f k ² ( h )

m

i 1 ⁱ 2 f i ²

Неравенство (2) определяет источник возникновения кавитации на регулируемом дросселирующем элементе, скорость течения жидкости на котором больше, чем на нерегулируемом сопротивлении

K  Pk (h)  Pнп pvk2(h)

Из анализа выражения (3) можно предложить следующие рекомендации по уменьшению или исключению кавитации в гидравлическом устройстве:

• -    уменьшение скорости v k ( h ) на каскаде дросселирования;

• -    увеличение противодавления на выходе дросселирующего элемента.

При неравномерной эпюре скорости течения жидкости критерий кавитации, рассчитанный по среднему значению vkср приводит к уменьшению запаса по кавитации. Введем понятие зоны кавитации, т.е. части области течения через каскад дросселирования, в которой возникают растягивающие напряжения, достаточные для образования каверн. Максимальная скорость потока, определяющая наибольшие растягивающие напряжения в зоне кавита- ции, равна

V max

Q

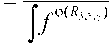
где φ – функция распределения ско- ростей по меридиональному сечению потока.

Из анализа критического числа К кр

P k ( h )   K кр ^{pv m 2 ax}   P нп        (5)

следует, что увеличение значения Vmax приводит к расширению зоны кавитации, а увеличение значения Pk(h)– к ее сужению.

Реализация допустимого числа кавитации в проточной части гидравлического устройства является одним из основных критериев, используемых при проектировании малошумных СУ ТС.

Рассмотрим некоторые принципы проектирования проточной части. Особенностью метода многокаскадного дросселирования является возможность перераспределения перепадов давления на отдельных каскадах дросселирования с целью реализации допустимого числа кавитации. При этом могут использоваться различные принципы распределения перепадов давления на n каскадах дросселирования:

равномерное распределение

. Р-Р

П1^ Kдоп (P1 P);

Pсл неравномерное распределение n2

Р> =РслП(1+  , i 1

В частном случае, принимая равный запас по кавитации на каскадах дросселирования Кi=K при условии μi=μ, получим аналогично работе [2]:

n ₂

^lg P

lg(l+ L)

2 K

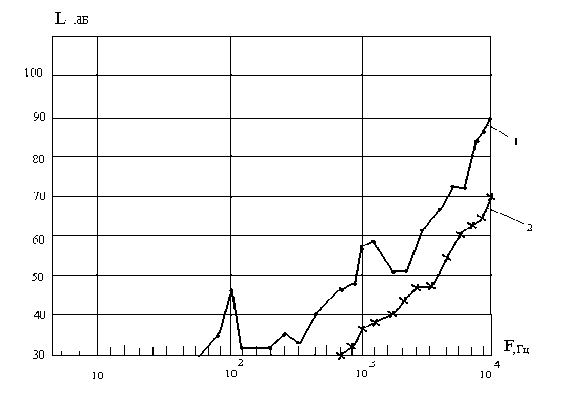
Рисунок 1 - Спектрограмма уровней вибрации гидроусилителей при h =3мм, Рнап=140 кгс/см², Q ном =160 л/мин: 1 – с двумя каскадами дросселирования; 2 – с четырьмя каскадами дросселирования.

Целесообразная область использо- вания двух указанных методов распределения перепадов давления определяется соотношением

•g p^

n ₂                P _сл

Включение в каскад дросселирования конструктивных элементов, реализующих вязкостные потери, существенно расширяет возможности обеспечения бес-кавитационного режима течения жидкости в соответствии с зависимостью

2nm

АРдоп =    , н fm1^^)

2      Kдоп i 1 fi j 1

Конструктивная реализация добавочного mlj члена         должна обеспечивать воз- j1jdj можность изменения вязкостных потерь в широком диапазоне регулирования, например, с помощью регулируемого конического щелевого диффузора с гладкой поверхностью. Увеличение диапазона регу- лирования возможно за счет искусственной шероховатости обтекаемой поверхности. Допустимое число кавитации учитывает условия на входе в проточную часть, на выходе и в щелевом зазоре. На рис. 2, 3 представлены спектрограммы уровней вибрации двух устройств с разными проточными частями, работающих на одинаковых режимах.

Виброактивность устройства, содержащего добавочные вязкостные потери в регулируемой проточной части, значительно ниже, чем в случае традиционной формы протонной части с потерями инер- циального типа.

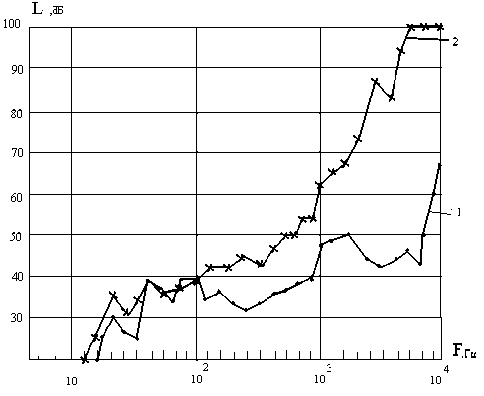
Рисунок 2 – Спектрограмма уровней вибрации гидроусилителей при Р нап =37 кгс/см², Р сл =10 кгс/см², Q=60 т/ч: 1 – с конической формой штока, 2 – с параболической формой штока

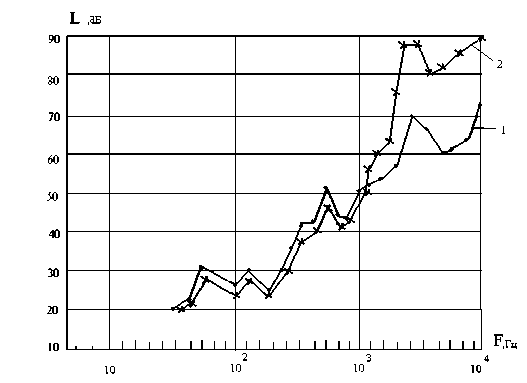
Рисунок 3 – Спектрограмма уровней вибрации гидроусилителей при Р нап =48 кгс/см², Р сл =25 кгс/см², Q=30 т/ч: 1 – скругленная дроссельная кромка; 2 – острая кромка

Используя некоторые допущения, принятые при рассмотрении акустического излучения, а также результаты, приведенные в работах [3] по оценке акустической энергии при смыкании сферической каверны, получим следующую связь акустической и потенциальной энергии:

4Л2

4 r    P ² ( t ) dt 0 , 3 Л R 0 P о,       (10)

pc                3

где: r – радиус сферы, на котором определяется величина акустического излучения; R 0 – начальный радиус сферической каверны; с – скорость звука в среде; Р ∞ – давление в зоне смыкания каверн; Р ( t ) – импульс давления при смыкании каверн.

Уровень эффективного значения звукового давления при кавитации получим в виде

1 P -В R ³

3 T _r 2 ^pc

L 20 lg ^{3 T r}     ,      (11)

p где β – доля потенциальной энергии, пе- реходящая в акустическую.

Расход парогазовой фазы, возникающий при действии растягивающих напряжений, с учетом работ [2] представим как функцию

Q r = а§ Q 1 K min ,         (12)

где α – коэффициент пропорциональности, определяющий соотношение площадей сечения кавитационного и бескавитационно- го потока.

Если ввести понятие среднестатистического радиуса R для пузырьковой формы кавитации, то расход парогазовой фазы равен

Q r  ⁴ л ^R ,                  (13)

где Т – период следования среднестати- стического пузырька.

Зависимость (11) с учетом выражений (12, 13) представим в виде:

L 20 lg   ^4л r ²

P 1 K min pc ^а Q

2х104

. (14)

Акустическая энергия при схлопы- вании каверн передается на корпус гидравлического устройства, возбуждает его вибрацию, которая распространяется по корпусу объекта.

Колебательная энергия, передаваемая через опорные связи [1] равна

W = Г|

q ² Mf 0²

где: η=0,1 – коэффициент потерь в амортизирующих креплениях; М – масса устройства; f0 – собственная частота колебаний амортизированного устройства; f – теку- щая частота; q – ускорение в точке контроля вибрации на частоте f.

Спектральная плотность акустической энергии, излучаемой через сферу ра- диусом r при аппроксимации однополяр- ным импульсом давления от смыкании сферической каверны [3], равна

W ( f ) p   ₍₄ л ² f ² + ¹ 2 ^{) 1 ,}

2л r          a ²

где а = eR₀

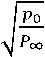
– постоянная времени, ха- рактеризующая прочес смыкания каверны радиусом .

Для расчета уровней вибрации, воз- никающих в условиях кавитационного течения жидкости через одно отверстие, при допущении, что колебательная энергия в процессе смыкания каверн передается через конструкцию гидравлического устройства без потерь, используя зависимости (15), (16), получим

L = W1 P 2 (2лr)"1 (4л2 f 2+11 a2 )-1 _ g          Wo

...- 10 1g M -20 1g f ₎₊30 1g f -72 ,    (17)

где            – уровень вибрации по ус- корению; P = -—уP 1- Kminppc^aQ .

4 r ²

При определении уровней вибрации в полосе 1/3 октавы и равномерной спектральной плотности получим вибрацию для i -ой полосы в виде:

_{L =101} P ² (2л r )" ¹ (4л² f ²+1 / a ² )- ¹ 2 f _

• ¹     g              W o

...- 10 1g M -20 1g f )+ 30 1g fi -72     (18)

В стационарном режиме работы гидравлического клапана основным источником вибрации, замеряемой на опорных и неопорных связях, являются пульсации давления в турбулентном потоке. Оценка влияния турбулентности на спектр вибрации является сложной научной задачей, строгое решение которой, очевидно, невозможно.

Турбулентные источники виброшу-моактивности в проточной части гидравлических приборов принципиально исключить нельзя. Интегральная оценка акустической мощности турбулентной струи N ак получена Лайтхиллом в виде :

Nк =K^'FVV / c ⁵,             (19)

где: K L – коэффициент Лайтхилла; F – площадь дросселирующего устройства; с – скорость звука.

Из (19) следует, что наиболее эффективным средством уменьшения шума является снижение скорости потока. Для гидравлических устройств с проточной частью на принципе инерционных потерь скорость струи равна

• ^Vc= 2 Др^РГу ,       (20)

где:  – коэффициент динамической вязко сти; – ускорение свободного падения.

Из (19) и (20) следует, что интенсивность турбулентных источников определяется, прежде всего, точностью согласования характеристик источника (насоса) и гидросистемы.

Для оценки частотных составляющих уровней вибрации от действия турбулентности, воспользуемся решением Кор-коса, которое позволяет заключить, что среднеквадратичное значение звукового 2

давления p на некотором расстоянии пропорционально   среднеквадратичному значению местной турбулентной пульсации давления p2   и четвертой степени характерной частоты этих пульсаций p2 « (1/С4 )«>4 pK2e„        (21)

Приближенный метод, положенный в основу расчета проточных частей гидроприборов, основан на имеющийся информации по результатам испытаний аналогов, которая позволяет принять некоторый частотно-зависимый коэффициент Nst, характеризующий передаточную функцию прибора Nst (f ) = q(f)/ p2 (f), где: q(f) -частотный спектр виброускорения на опорных связях прибора, a p2 (f) - спектр среднеквадратичного значения давления потока [3]. Опуская промежуточные выкладки, представим уровни вибрации по ускорению в виде:

64л²р _A. _r4 r 4 V*⁴A. ²

L = 10 1g         Nstf^{4 1 ; ;   ;} «1₂а₂з - ...

• c ⁵ w ₀              r_i ^{2                   ,}

• ... -10 1g M -20 1g f 0+ 30 f -72 ,   (22)

При расчете, боковая поверхность конуса, на которой происходит дросселирование, разбивается на n частей площа-A дью     Ai , а расстояние от этих фрагмен- n тов площади до расчетной точки составит 2i. По результатам обработки большого количества экспериментальных данных определены значения Nst(f), которые целесообразно использовать при расчетах гидроприборов. Значения Nst относительно 10-8 приведены в табл. 1.

Из анализа коэффициента N st (f) следует, что резкий спад функции наблюдается на частотах f > 3 150 Гц, следовательно, конструктивно приборы способны интенсивно поглощать высокочастотные колебания [2].

Анализ результатов расчета и экс- периментальных данных показывает, что уровни вибрации, определенные по (22) с точностью до ±5 дБ, описывают процесс в диапазоне частот 1000-10000 Гц.

В зоне частот f<1000 Гц формула (22) не работает, в связи с чем можно предположить, что низкочастотные колебания определятся в основном резонансными колебаниями системы: гидравлическая система – гидроприбор.

Данный подход дает достаточно хороший результат в зоне частот 1000 Гц – 10000 Гц и позволяет при проектировании устройств осуществить экспертную оценку альтернативных вариантов.

Для гидравлических приборов нестационарным режимом является «перекладка» регулирующего органа, вызываю- щая изменения расхода жидкости в трубопроводе. При этом возбуждается вибрация прибора и трубопровода из-за действия волновых процессов. Другим проявлением волновых процессов является возбуждение резонансов в трубопроводе вследствие действия периодического возбуждения, возникающего из-за автоколебаний или пульсационной составляющей давления, генерированного насосом гидросистемы. Волновые составляющие возбуждают низкочастотные колебания, борьба с которыми в гидросистеме малоэффективна, поэтому необходимо их минимизировать при проектировании гидроприбора и гидравлической системы в целом. Вибрация неопорной связи по ускорению определяется зависимостью:

Таблица 1 – Значения N st ( f )

f , Гц	1000	1250	1600	2000	2500	3150	4000	5 k	6,3 k	8 k	10 k
N st /10-8	54,3	49,7	48,56	48,22	46,52	43,31	32,55	24,08	15,7	7,82	9,75

L 20 lg

R ²

5 E ₁ S ²

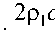
l

dQ dt dt

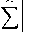
n 1

4 a ² l ⁴

l ²

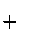
a

4 a ² l ⁴

1 n

2  33

I 3 _{c 1} 3 _{a 2}

l ²

1 n

1 ' 4

n

2 J

44 c ₁

44 c ₁

3 l ²

1 n

1 ' 2

n

2 J

22 c ₁

cos СО nt +

22 c ₁

sin со n t

X _l R 2 h + 40 lg - ⁿ

2л

120 ,

где: R – радиус трубопровода; dQ/dt – скорость изменения расхода при нестационарном режиме работы прибора; E1 – модуль упругости трубы; S – площадь поперечного сечения трубы; l – длина трубы; a – коэффициент потерь на трение; ц – коэффициент динамической вязкости; со n – частота n-ой гармоники. Значение со n оп- ределяется          из          условия

n

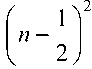
22 c ₂

l ^{2 a}

Результаты

расчёта

третьоктавных

уровней вибрации гидроприбора при нестационарном режиме работы сопоставимы с экспериментальными данными [3].

Следует отметить. Что данный расчёт производится без эмпирических коэффициентов соответствия, имеющих, обычно, час- тотную зависимость. Возбуждение труб строго детерминировано и в расчёт принимаются только упругие колебания, что является справедливым при X »2 7ГR. В зоне низких частот возможны отличия на 10 – 12 дБ, что, вероятно, является влиянием изгибных колебаний трубопровода, которые в расчёте не определялись. В зоне высоких частот возможные расхождения расчётных и экспериментальных значений определяются кратковременным действием кавитации на переходных режимах, вызванной погрешностью автоматического отслеживания перепада давления на приборе.

Значимость волновых составляющих определяется критерием Эйлера Е в форме

E  (pст   pнест) /( рV 2 ), где: Рст и Рнест – давления в стационарном и нестационарном режимах работы прибора соответст- венно; V – скорость жидкости в трубопроводе. С учётом имеющихся решений величина критерия Эйлера равна:

E = B ² H I B (- 1 )

B ²    3   ^,

(24),

где

B = (0,3164цl)/(2 Re0’25 d), число, ха-

рактеризующее затухание волновой со- dV  2

ставляющей; H = 2l   / с - критерий го- dt    1

мохромности;           – безразмерное

2l / c время, выраженное в масштабе фазового времени трубы, т.е.     1,2,3,.... Величина допустимого значения критерия Эйлера, при котором можно не учитывать волновые процессы с точки зрения упругой реакции неопорной связи прибора, зависит од допустимых уровней вибрации прибора.

Значение гидродинамического шума L _ГДШ при нестационарном режиме в случае произвольного сигнала, когда функцию пульсационной составляющей расхода можно представить Фурье-разложением

L ГДШ — 20 lg Po

2 1 c 1 ²

t ₁

_c, X k Q2 cos I n-- |—( t- t) dx + ...

Sl n 1 0 2

2 c

2 T                  t

...+ X--\Q (t )cos mtotdt\cos mo Teos m1 T0                 0

n— —( t- t) dx +... (5),

2   c 1

2 T                  t

...+ ^   Q (t )sin m^tdt Jsin mcoTeos m1T0                0

где: Р0 – пороговое значение давления для ГДШ; Q(t) и Q2 – расход жидкости через прибор и изменение расхода при n— —(t- t) dT k

• 2   c 1

000 Гц – 10 000 Гц и позволяет при проектировании устройств осуществить экспертную оценку альтернативных вариан- нестационарном режиме соответственно. Уровни вибрации патрубков от воздействия ГДШ могут быть получены расчётом их деформации как упругих элементов.

Т.о. можно сделать следующие выводы:

• 1.    Наиболее существенно на уровни вибрации влияет конструкция каскада дросселирования гидравлического устройства, а также параметры течения жидкости. С увеличением давления Р ∞ , и сохранением числа кавитации вклад в виброактивность возрастает, т.е. для многокаскадного устройства с равным запасом кавитации на каждом каскаде дросселирования определяющими по виброактивности являются первые по течению жидкости каскады.

• 2.    Приближенный метод расчета виброактивности гидроприборов при учете турбулентности потока дает достаточно хороший результат в зоне частот 1

• 3.    Снижение влияния волновых процессов при нестационарных режимах работы возможно при проектировании гидросистемы в целом выбирая переходные режимы с учетом минимального ГДШ.

тов.