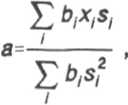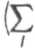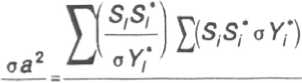Снижение влияния шумов на интерпретацию спектров в Фурье-спектроскопии

В настоящее время Фурье-спектрометры применяются во многих прикладных и фундаментальных исследованиях [1]. Для любых приложений принципиальным является вопрос о природе, характере шума в получаемых спектрах и методы борьбы с ними. Измеряемая Фурье-спектрометром интерферограмма представлена конечным числом дискретных значений А^^-.-Х» регистрируемых через равные интервалы оптической разности хода. В силу отличий реального Фурье-спектрометра от идеального данные значения отличаются от истинных St^.-.S^ Искажения интерферограммы можно разделить на систематические (воспроизводящиеся от скана к скану) и случайные (не воспроизводящиеся). В литературе большое внимание уделено борьбе с систематическими искажениями (например устранение влияния систематической ошибки определения /-той фазы [5]. Известно, что случайные искажения (шумы) могут приводить к тому, что в полученном спектре появляются коррелированные шумы. Однако обычно ограничиваются только констатацией этого факта [2]. Случай, когда шумы в разных точках скоррелированы, является нетипичным для многих приложений (например, появление такого шума в спектре, полученном на дисперсионном спектрометре, говорит о том, что прибор никуда не годится), но не для Фурье-спектроскопии. Поэтому в данной статье предлагается относительно простой метод уменьшения влияния такого шума на точность определения концентрации индивидуальных веществ по спектрам поглощения, а также несколько способов определения корреляционной функции. Улучшение точности достигается за счет того, что подгонка теоретического спектра к экспериментальному производится не непосредственно в полученном спектре, а после выполнения дискретного Фурье-преобразования. Ниже можно найти математическое обоснование такого метода, здесь же поясним смысл наших действий: пусть исходная интерферограмма есть 5(<$), тогда найденный спектр есть АЦ v) (Фурье-преобразование от 5(6)). Если заданное вещество имеет ярко выраженный спектр поглощения от vmin до vm„, то только спектр в этой области имеет значение для определения концентрации. 5(5) также несет в себе всю информацию о спектре поглощения, однако в ней отделить "лишнюю часть" нужно по-другому. А именно, нужно произвести Фурье-преобразование, домножить результат на функцию, которая есть единица внутри интересующего нас интервала частот и ноль вне этого интервала (прямоугольная функция), а затем выполнить обратное Фурье-преобразование. В силу свойств Фурье-преобразования это эквивалентно свертке интерферограммы с Фурье-преобразованием отпрямоу-гольной функции (sinc(’)).

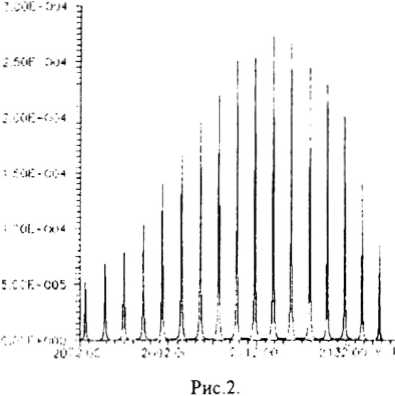
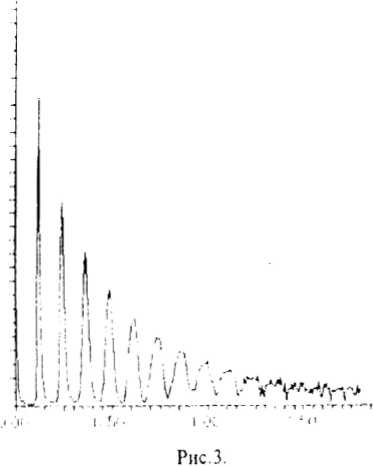
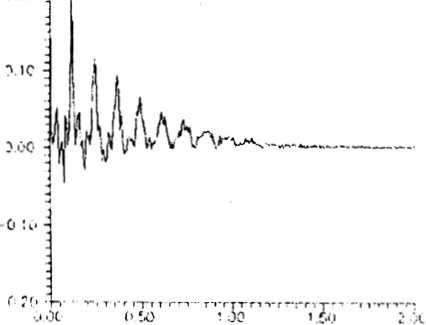
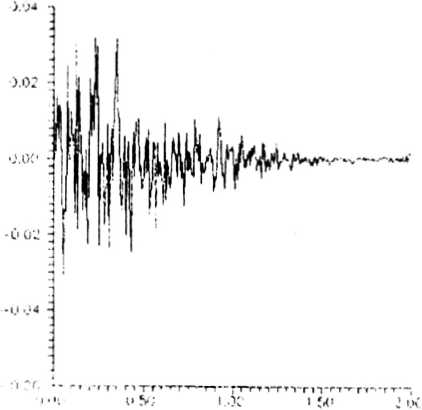
Теперь перед нами встает вопрос, что лучше: подгонка экспериментального спектра под теоретический спектр или подгонка экспериментальной интерферограммы к теоретической интерферограмме? И хотя с точки зрения математики это совершенно эквивалентно (спектр и интерферограмма связаны взаимнооднозначно), оказывается, что проще и быстрее второй подход, поскольку при этом мы работаем с интерферограммой, которую получаем непосредственно в эксперименте. Таким образом, именно такой анализ следует считать наиболее естественным в Фурье-спектроскопии.

Источники шумов

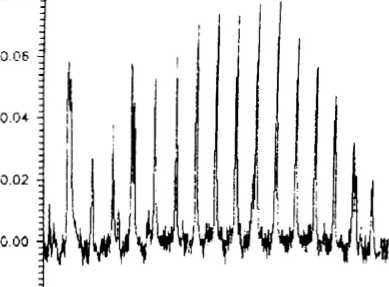
Случайный процесс есть случайная функция от независимой переменной I. Для описания такого процесса удобно пользоваться корреляционной функцией [31 Д(г,,г2)=ЛД.х(г1)х(гг)], где Мозначает усреднение по множеству наблюдений. Если R^v^ есть функция от t=i

Ф^рШ^У"Я(т)ехр(-/(.)1т)Лб(ы1 -м2) = -Ф(о1)6(«1-о2) .

Обратно, если ЯЦр/^Т^/,)^/,-^) (шумтипа 2), то

Ф(о1,и2)=УА(/)ехр(-/(ы1-о2)^сУ/-Ф(о)1-ш2) (соотношения Хинчина - Винера). Особо отметим случай, когда 2?(/1Д2)=(/1-/2) (шум типа 3 или белый шум), для которого Ф(й>р<Й2)=й (W,-^).

Применительно к Фурье-спектроскопии данные соотношения означают, что скоррелированные шумы в интерферограмме дают некоррелированные шумы в спектре (причем средний квадрат шума может зависеть от длины волны). Наоборот, зависимость квадрата шума в интерферограмме от фазы приводит к появлению скоррелированных шумов в спектре.

Рассмотрим основные источники шумов в Фурье-спектроскопии.

• 1)    Нелинейность регистрирующей системы. В данном случае регистрируемую интерферограм -му 1(6^ можно представить в виде ф(б_п)=(7(7(<$_п)), где G - характеристика регистрирующей системы. Если 7_Г(5_П) регистрируется с погрешностью М(6_п), и Д7(6_П)<7(Д_П), то 7Xn)M^^ В случае слабой нелинейности ^^WWW+t^AW

• 2)    Ошибки определения оптической разности хода. 7_г(5_п)^7(ф+Д_п) следуя (2) представим Д_п в виде ^_n=d°+d_n'+d_n², d° - постоянный фазовый сдвиг. d„¹ - случайный фазовый сдвиг. Д„² -систематическая погрешность. Приближенно 7_г(ф)=7Ш+(д7/д<5)(дЧд; + /С).

• 3)    Нарушение юстировки при движении зеркала. Регистрируемую интерферограмму представим в виде 7_Г(Д_П)= 7( 5_П) Д д_п), TW опять представим в виде суммы чисто случайной функции Т’ДгД ^и систематической (повторяющейся от скана к скану) части /₂(5_П).

• 4)    Шумы фотосопротивления и шумы квантования АЦП будем считать их чисто случайными некоррелированными шумами.

Таким образом можно считать, что регистрируемую интерферограмму можно представить в виде 7г(дп)=7(7(ф))+Д(7(п))Дп, где Щ-операторы, Дп - шум, не воспроизводящийся от скана к скану и средний квадрат которого не зависит от н. Отличия 7 от единичного оператора может обуславливать серьезные искажения спектра (много большие, чем случайные шумы). В [5] показано как можно уменьшить такие искажения за счет анализа деформации контура хорошо известной изолированной узкой линии. Будем считать, что 1=1 (т.е. либо отличие 7 от единицы мало, либо проделана процедура восстановления всего спектра по "хорошо известным кускам", подобная описанной в £5]). Остановимся подробнее на случайных шумах. Дополнительно предположим, что они некоррелированы, т.е. функция корреляции имеет вид К^б^б^ЦЧКб^а'ЧД^, где ^(Д) - дисперсия Д Дц- дельта-символы Кронекера. Со гласно с оотношению Хин чина - В инератакие шумы при взятии Фурье-преобразования трансформируются в шумы с корреляционной функцией (с точностью до множителя)

Ф^1,Уг)=£ L₁²(/(6^)exp(-/(v₁ -v^^tv,-_V2). п

Данная формула позволяет находить вид корреляционной функции при определенных предположениях относительно 7, и виде спектра, Кроме того, она показывает, что нескоррелиро-ванный шум в спектре может возникать только если 7, (7) “const (единственным примером такого шума из разобранных выше является шум квантования АЦП).

Метод учета функции корреляции

Предположим, что необходимо измерить концентрацию вещества с известным спектром по спектру поглощения. Для этого достаточно ограничиться лишь небольшим участком спектра от vmin до vmax, где данное вещество имеет сильные линии поглощения. В данном диапазоне нам известен ряд экспериментальных значений хрх2,...,хп при частоте vpv2,...,vn соответственно. Обозначим значения теоретического спектра при тех же частотах за s1,s2,...,5n. Необходимо найти с какой долей заданный спектр, т.е (5} входит в экспериментальный, т.е. {л;}.

Рассмотрим кратко математическую сторону вопроса: Пусть х=й5,+ц, где у - не-скоррелированы и распределены по Гауссу, причем дисперсия у есть а,. Тогда функция плотности вероятности вектора х запишется в виде [4[

Р^.Ч.....x;Mvaa.....,а>

2    2

~°1 Og -

о/^рЦГА^ as)²]

В качестве оценки неизвестного параметра а возьмем оценку метода максимального правдоподобия. Эта опенка по определению соответствует максимуму функции плотности вероятности, что эквивалентно минимизации

L^b^x-as)², где b = \ /а^ Т.е. методу наименьших квадратов.

Если про вид распределения у, ничего не известно, естественно все же попытаться минимизировать! при не которых фиксированных весовых коэффициентах b_v Тогда из условия обращения в ноль дЬ/да получим

коэффициент а, определяемый формулой (1) можно рассматривать как случайную величину. Нетрудно найти дисперсию а. Мы найдем ее в случае, когда д=0, т.е. сигнал есть чисто случайная величина:

м[Е ь^

^[52 bj X] Sj *252 52 Ь(Ькх,хк5,$к\ i                       i к                       J

(во втором члене суммирование только по / не равном к), учитывая, что Л/Jх^ 1=0 при i не равном /, получим в итоге

Е.2 2 2

• b, Sj Oj о a²-—------- (2)

b,s?f

У нас еше остался произвол в выборе Ь, и его естественно использовать для снижения оа. Необходимое условие минимума а а² по Ь_т запишется в виде:

даа² _ 2ti_mS_ma_m5Z ^Sj 2s_m^ Ь, S, a, ^

а*>/ fcbrf "

, E b,s? s^a²„b_m-o’b)

E.^

отсюда b=\/a². Формула для а приобретает вид:

-а^ ^/о²у'. О)

Перейдем теперь к случаю скоррелированных шумов. Пусть х=а5,+у, где у - случайные скоррелированные величины с функцией корреляции R(y_l,y)=R_<=RU-j). В частности ^²=5(0) не зависит от / и в методе наименьших квадратов естественно выбрать единичные весовые коэффициенты (хотя а уже нельзя искать по формуле (2)). Можно предложить другой подход. Применим метод наименьших квадратов не к самому спектру, а к Фурье-преобразованию от спектра. Пусть результат дискретного Фурье-преобразования от s и х есть 5 и А'соответственно (5) и X, комплексные величины). Основная идея заключается в том, что после Фурье-преобразования у, превратятся в )(, которые будут нес коррелированы, а aY, согласно соотношениям Хин чина-Винера является Фурье-преобразованием от функции корреляции R(i-f). Итак, найдем, с какой долей ^ входит в А/. Будем искать значение Л, минимизирующее функционал L =52 В^Х,-AS)(X. -AS)"

при фиксированных В,. С учетом комплексности 5, и А' формулы для Л и аА примут вид:

аХА№>       <4)

Е 8,5,5"

^Х£^Х .   (5)

(Е 8,5,5^

Оптимальными являются 5=1/^ при этом oA^S^/oY^ (6)

Значение а, полученное по формуле (1) с единичными весовыми коэффициентами, в силу равенства Парсеваля совпадает с А, вычисленным по формуле (4) при 5=1. Действительно, £А'5/=£х^" и £5,5/=5)5,5/.

Таким образом выигрыш в точности (отношение дисперсий аа с единичными Ь, и аА с оптимальными В,) есть

° А2     ES,srf

Данное отношение может принимать значения от 1 (нет выигрыша) до +~ в зависимости от корреляционной функции и вида Л’.

Методы получения корреляционной функции

Отметим, что Фурье-преобразование как от получаемого, так и от искомого спектров комплексны. В то же время искомое значение А вещественно в силу физического смысла. Таким образом даже если функция корреляции шумов нам заранее неизвестна, при отсутствии в данной части спектра других веществ можно считать, что Im(^5’")/|5J есть чистый шум. Функцию корреляции в таком случае можно получить разбивая сигнал на группы (содержащие достаточное число точек) и производя усреднение квадрата такого шума по каждой группе.

Другой возможный метод определения функции корреляции состоит в выборе другого участка спектра, где сигнал заведомо отсутствует (такой участок должен располагаться неподалеку от первого). Фурье-преобразование такого участка также разбивается на группы и производится усреднение по группе.

Еще один подход заключается в статистической обработке многих спектров поглощения и статистическом определении корреляционной функции. В силу того, что функция корреляции зависит не только от свойств конкретного прибора, но и от самого спектра, такие измерения необходимо проделывать всякий раз, когда вид спектра существенно меняется.

Наконец, последний метод состоит в изучении специфики конкретного прибора, нахождении источника шума и вида функционала Л, для них. В таком случае по интерферограмме можно сразу находить вид корреляционной функции.

Если функция корреляции получена, то остается применить подгонку Фурье-преобра-зованного спектра с оптимальными весовыми коэффициентами. Коэффициент выигрыша, однако, зависит от многих факторов (конкретной мод ели Фурье-спектрометра, вида экспериментального и теоретического спектров). Поэтому в качестве иллюстрации продемонстрируем применение изложенных выше принципов на примере определения концентрации угарного газа (СО) по спектру поглощения, полученному на Фурье-спектрометре ФСЗ-01.

Вид х, (экспериментальный спектр в диапазоне 2072-2143 обратных сантиметров), у (теоретический спектр СО, Р-ветвь), |5J (модуль Фурье-преобразования от теоретического спектра) показаны на рис. 1,2 и 3 соответственно. На рис.4 и 5 показаны Ке(5,'АУ|5’|)

оха

-0.С2 :

"0,04 4—г-т-ГГп-Г"|-т,г-'Т^1-г'т-Т‘гттт--т—i--1—'Г-1 I —'Г

2072 1)0     209 2 СО 2 Н 2 00      213 7 СЮ V 1

Рис.1.

и im^/A'/ISD- Согласно вышеизложенному 1т(5,’АУ1^1) есть чистый шум. Рис.5 показывает, что амплитуда этого шума совпадает с

ростом /, что означает скоррелированность шумов в исходном спектре (т.е. л;). Это как раз и означает, что в данном случае точность можно улучшить, если использовать минимизацию взвешенной суммы квадратов отклонений X от A Re^'A'/ISJ), если весовые коэффици-е н т ы обратно пропорциональны (Im(5'.¥/|A,|)2), где угловые скобки означают усреднение по группе из нескольких ближайших точек (мы использовали около 20-ти точек для такого усреднения, общее число точек в данной части спектра было равно 1024).

0.20 -

Рис.4.

Рис 5.

квадратов с единичными весовыми коэффициентами оказалась в 5-6 раз хуже, чем точность описанного нами метода. Такой выигрыш является существенным (в частности для задач экологического контроля), однако он не исчерпывает всех достоинств данного метода.

В заключение сделаем два замечания:

• 1)    Регистрируемый спектр в действительности является сверткой теоретического спектра с аппаратной функцией. Для учета этого обстоятельства в предлагаемом методе необходимо домножить Фурье-преобразование от теоретического на Фурье-преобразование от аппаратной функции. (В простейшием случае - на функцию аподизации).

• 2)    Данный алгоритм автоматически переносится на случай определения концентраций нескольких веществ, спектры которых в данном диапазоне перекрываются. Единственное отличие состоит в том, что первый метод определения функции корреляции уже не годится.