Собственные частотные спектры пространственной структуры

• 1    Введение / Introduction

Металлические ферменные конструкции имеют ряд преимуществ по сравнению конструкциями из плит, блоков и ферм из дерева или композитных материалов. Прежде всего это надежность, прочность и простота в использовании и монтаже. Именно поэтому такие конструкции часто используется в строительных работах. Расчет пространственных конструкций производится, как правило, в численной форме на основе метода конечных элементов. В [1] разработана трехмерная нелинейная модель конечных элементов для расчета взаимодействия стальной и бетонной части фермы. Численный расчет фермы в [2] при изучении механизма разрушения стальных арочных стержневых конструкций, подвергающихся сильным землетрясениям, дополняется серией испытаний на вибростенде. В [3] даны результаты экспериментальных и численных исследований сопротивления сжатию тонкостенных сечений, и их прочности на сдвиг. В статье [4] модальные эксперименты на вибрацию большой развертываемой в космосе антенны с кольцевой ферменной конструкцией сравниваются с результатами численных расчетов. Аналитические расчеты пространственных конструкций достаточно редки. В монографии [5] теоретические основы метода конечных элементов в задачах строительной механики представлены в виде классического смешанного метода. На основе этой теории разработаны алгоритмы решения задач статики, динамики и устойчивости конструкций различного типа, не уступающие по своей простоте и эффективности алгоритмам на основе этого же метода в виде метода перемещений. В работе [6] с применением системы символьной математики Maple представлены точные трехмерные упругие решения для некоторых статических и динамических задач изгиба многослойных анизотропных прямоугольных пластин. Они получены методом начальных функций без использования каких- Kirsanov, M.; Luong, C.

Natural frequency spectra of spatial structure

либо гипотез о характере напряженно-деформированного состояния линейно-упругих анизотропных конструкций. Разработаны два вычислительно устойчивых алгоритма метода, расширяющие область его применения. Представленные результаты иллюстрируют некоторые возможности разработанных устойчивых алгоритмов. Проведен анализ многослойных пластин под действием сосредоточенных статических и гармонических динамических нагрузок. В [7] расчет устойчивости ферм выполнен в нелинейной постановке. Приближенное аналитическое решение в системе Maple для деформации прямоугольной пластины с трещиной в виде тригонометрических полиномов строится методом суперпозиции по двум решениям, полученным методом начальных функций [8].

Для регулярных конструкций аналитический расчет выполняется, как правило, с использованием метода индукции, позволяющим получить результаты для широкого класса конструкций, отличающихся только порядком (например, числом панелей). Для плоских ферм это работы [9,10]. Расчет собственных частот по формуле Донкерлея [11,12] пространственной консоли выполнен в [13], для плоской фермы – в [14]. В [15] найдена аналитическая форма зависимости первой частоты свободных колебаний купольной фермы от числа панелей в основании конструкции. Формула для первой частоты двухпролетной плоской фермы с использованием метода индукции получена в [16]. В работе [17] выведена нижняя граница собственной частоты плоской фермы Финка. Известна и двухсторонняя аналитическая оценка первой собственной частоты плоской регулярной фермы [18]. Общие вопросы существования и расчета статически определимых регулярных стержневых систем рассмотрели Hutchinson R.G. и Fleck N.A в [19,20]. Большой вклад в теорию таких систем с учетом вопросов оптимизации внес Kaveh A. [21,22]. В справочнике [23] приведены схемы регулярных плоских ферм и формулы для расчета их прогибов. Статический расчет в аналитической форме для регулярной составной пространственной фермы с применением системы Maple выполнен в [24]. Расчет оптимальных размеров регулярной фермы с учетом ползучести дан в [25]. Обзор некоторых аналитических решений задачи о деформациях регулярных плоских ферм выполнен в [10].

В данной работе ставится задача вывести аналитическую зависимость нижней и верхней оценки частоты колебаний пространственной фермы от количества панелей. Использованную методику можно использовать и для других конструкций регулярного типа.

• 2    Материалы и методы / Materials and Methods

  2.1    Конструкция фермы

2.2    Собственная частота колебаний

Конструкция покрытия состоит из замкнутого контура отдельных пирамид высотой h и размером a х а в плане (рис. 1).

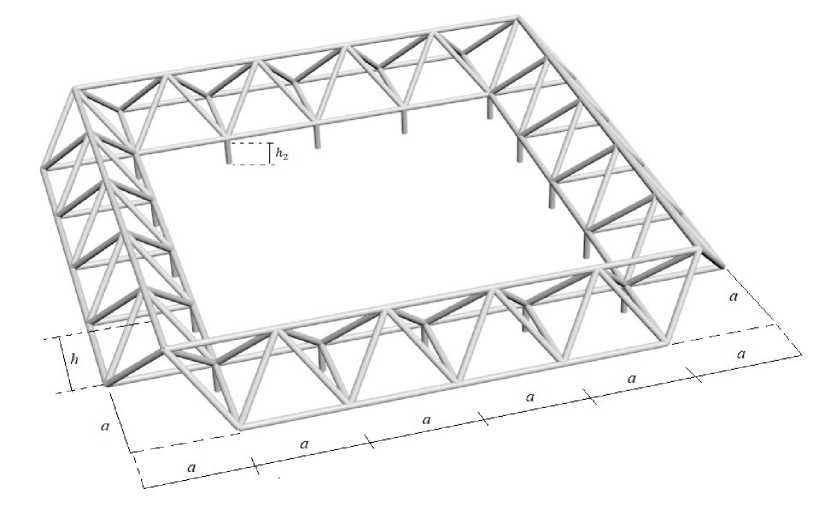
Рис. 1 – Конструкция покрытия, n =6

Fig. 1 – Coating design, n =6

Вершины стержневых пирамид соединены верхним квадратным контуром. Нижние грани пирамид образуют два контура. Внутренний замкнутый нижний контур конструкции закреплен на вертикальных опорах и четырех дополнительных взаимно перпендикулярных связях по углам. Внешний открытый нижний контур фермы образует консольную часть конструкции. Вертикальные опорные стержни имеют длину h ₂ . Вся конструкция состоит из N = 36 n - 48 стержней, включая стержни, моделирующие опоры. Количество внутренних шарниров 12 n - 16 . Прогибы этой конструкции и частота собственных колебаний по Донкерлею в аналитической форме для произвольного числа панелей рассчитаны в [26].

Значение первой (наименьшей) собственной частоты колебаний является одним из важнейших динамических свойств при расчете динамики конструкций. Как правило, расчет собственных частот выполняется численно на основе различных вариаций метода конечных элементов. Аналитические методы доступны только для верхних и нижних приближенных оценок частоты. Суть этих методов в том, что они основаны на вычислении парциальных частот, значения которых в ряде случаев могут быть найдены аналитическими методами. При этом аналитическая оценка может быть обобщена на произвольное число панелей индуктивным методом.

Инерционные свойства конструкции моделируются массами m в узлах фермы. В простейшей формуле массы грузов m одинаковые. Пренебрегая горизонтальными перемещениями узлов, колебания узлов рассматриваются только в вертикальном направлении. Число степеней свободы системы грузов фермы порядка n равно числу узлов K = 12 n - 16 . Динамические уравнения системы масс в матричной форме записываются следующим образом:

mI_KZ + D_KZ = 0.                                    (1)

Здесь Z - вектор вертикальных смещений масс в узлах фермы, Z — вектор ускорений, I_K — единичная матрица, D_K — матрица жесткости. В случае гармонических колебаний с частотой го справедлива связь Z = -го ² Z . Матрицей, обратной к матрице жесткости D_K , является матрица податливости B_K . Элементы этой матрицы вычисляются с помощью формулы Максвелла - Мора:

N bi,j=ZSa*'Saj'la /(EF)■                                        (2)

a= 1

Введены стандартные обозначения: b ij — перемещение узла i от действия единичной вертикальной безразмерной силы, приложенной к узлу j, 8 0(1¹ ' — усилия в стержнях с номерами α от действия единичной силы, приложенной к узлу i , где расположена масса m по направлению движения массы, l _α – длина стержня с номером α , EF — продольная жесткость, принятая для всех стержней одинаковой.

Умножением уравнения (1) на матрицу BK, с учетом замены Z = -ro2Z , соответствующей гармоническим колебаниям zk = uk sin(rot + ФоХ                                           (3)

задача сводится к проблеме собственных значений матрицы B_K : B_KZ = 1 Z , где 1 = 1/ ( го ² m ) — собственные числа матрицы B_K , ω — собственная частота колебаний. Отсюда ω= 1Л т й х ) .

Усилия S a ¹ ' в стержнях фермы, входящие в элементы матрицы B_K , определяются из решения системы уравнений узлов фермы, в число неизвестных которой, входят также и реакции опор. Для фермы с произвольным числом панелей в общем случае невозможно получить аналитические решения. Приближенные методы применяются для получения оценки первой частоты снизу и сверху.

2.3    Энергетический метод. Оценка сверху

Суть метода Рэлея основана на законе сохранения энергии. В каждом цикле гармонических колебаний происходит переход деформированной потенциальной энергии в кинетическую и наоборот, тогда равенство выражается следующим образом:

Kirsanov, M.; Luong, C.

Natural frequency spectra of spatial structure

T = П max max

.

Система состоит из K одинаковых масс m , расположенных в узлах конструкции. Кинетическая энергия системы имеет вид:

K

T = V mv2 i i=1

Согласно формуле (3) вертикальная скорость массы i имеет вид: v₄ = z_ = ю u cos( m t + ф ₀) .

Поскольку cos( m t + ф ₀) <  1 , максимальная кинетическая энергия имеет следующий вид:

K

T = -2mV и2/2, max i=1

где амплитуда вертикального смещения рассчитывается по формуле Максвелла – Мора: NN и, = у S(Р)S(il / (EF) =py SIР)S(il / (EF) = Рй..

i / -v a a a ' v                         a a a 1 x ' г a=1

Введены обозначения: S a^P ) — усилие в стержне a = 1,..., N от действия нагрузки Р , распределенной по узлам, S ai ) — усилие в том же стержне от одиночной (безразмерной) нагрузки, приложенной к массе с номером i , S a^Р ) = S'a^Р ) / Р . Форма колебаний системы нагрузок с первой частотой близка к форме прогиба конструкции от равномерной нагрузки. Таким образом, (6) принимает вид:

K

T = Р ² - ² Т mU ² / 2,                                    (8)

max           /       г г=1

N где Ui = ui / Р = У SaРSaiЧа / (EF) — амплитуда перемещений массы с номером i под действием a=1

распределенной нагрузки, отнесенная к величине P .

Потенциальная энергия деформации стержней фермы от действия распределенной NN нагрузки имеет вид: Птах = У S(aР)Аla/2 =У (SaР))2la /(2EF). Из-за линейности задачи по a=1

K нагрузке справедливо выражение S^P) = P^ S^1). Следовательно:

i = 1

N    K              KNK

П = Р2У ,S(Р)у ,S(il /(2EF) = Р2У yS(Р),S(il /(2EF) = Р2У й. /2.

max         / .J a / j a a >         '         / -J / a a a >         '         / -J г a=1       i=1                                i=1 ai

Из (4), (8), (9) следует формула Рэлея для верхней оценки первой частоты колебаний фермы:

KK

-R =У Ui / У mU2(10)

i=1

Для получения требуемой зависимости частоты от количества панелей необходимо получить перемещения U i как функцию от n . План решения следующий: 1) расчет перемещений масс с номером 1 для различных значений n с последующим определением общего члена последовательностей й 1 (п ) , 2) аналогичный расчет перемещений масс с номерами 2, 3, 4, ._. 3)

обобщение формул й 1 ( п ), й ₂( п ), U ₃( n ),... по массовому числу и получение искомой зависимости

KK йк(n), 4) вычисление общих членов сумм У йi и У й2.

i = 1           i = 1

Расчет перемещений для ферм с разным числом панелей показывает, что вид решения

K

У й ,. не зависит от порядка фермы n . Числитель и знаменатель в (10) вычисляются отдельно. i = 1

Числитель имеет следующий вид:

K £c = (gaa 3 + gc3 + ghh 3)/(h2 EF),                           (11) или в более компактной форме: K £ C = £      3 /(h2EF),                          (12) i=1           a=[ a, c, h ] где коэффициенты ga, gc, gh получены методом индукции, обобщением ряда решений для

различных n :

n = 3, ^ й = (784 a 3 + 125 c 3 + 1600 h 3)/ (16 h 2 EF ), i = 1 n = 4, '£Ui = (147 a 3 + 19 c 3 + 256 h 3)/( h 2 EF ), = 1 n = 5, ^й^ (5024 a 3 + 609 c 3 + 7744 h 3)/(16 h 2 EF ), i = 1                                                                             (13) n = 6, '£uii = (2476 a 3 + 269 c 3 + 3136 h 3)/(4 h 2 EF ), = 1 n = 7, ]T i/ i = (19824 a 3 + 1741 c 3 + 18496 h 3) / (16 h 2 EF ),

В результате получаются следующие коэффициенты:

g a = (9 n ⁵ - 13 5 n ⁴ + 815 n ³ - 193 5 n ² + 1946 n - 700)/20,

g c = (36 n 2 - 96 n + 64),                                                 (14) g h = (6 n 3 - 9 n 2 + 20 n - 16) /16.

Знаменатель (10) имеет более сложный вид:

K £ mu2k = £ mf apa 3 P 3 / (h 4 E 2 F 2),                            (15) k = 1                a , P = [ a, c, h ]

Обобщение ряда решений по индукции для некоторых случаев имеет следующий вид:

K n = 3, £ йь = (167680a6 + 4113c6 + 512000h6 + 51416a3c3 + 501760a3h3 + 80000c3h3)/(1024h4E2F2), i=1

K n = 4, £ui = (32072a6 + 527c6 + 81920h6 + 7936a3c3 + 89088a3h3 +12288c3h3)/(32h4E2F2), i=1

K n = 5, £ui = (3490688a6 + 52595c6 + 7434240h6 + 824928a3c3 + 9281536a3h3 +1201024c3h3)

= 1

/ (1024 h ⁴ E ² F ²),

K n = 6, £Hi = (344024a6 + 4221c6 + 501760h6 + 75364a3c3 + 795648a3h3 + 89152c3h3)/(32h4E2F2),

= 1

...

Из решения рекуррентных уравнений получаются коэффициенты:

f aa = (465 n ⁹ - 12555 n ⁸ + 154191 n ⁷ - 1092861 n ⁶ + 4777304 n ⁵ - 12857040 n ⁴

+ 21128104n3 - 20600184n2 +10938576n - 2436000) /13440, fcc = (24n5 - 60n4 +121 n3 +18n2 - 96n) /1024, fhh = 180n3 - 840n2 +1280n - 640), fac = (765n7 -11340n6 + 69384n5 -195405n4 + 343000n3 - 438060n2 + 349256n -117600) /13440, fah = (27n6 -441 n5 + 3045n4 -9901n3 +16278n2 -13208n + 4224)/6, fch = (30n4 - 85n3 + 42n2 + 48n -32)/8.

Таким образом, верхнюю оценку первой частоты фермы в зависимости от количества панелей можно получить по формуле:

3 EF E g_aa ³

^W R. = ^h

⁴ m E ^^{а 3 p}

. 3

Нижняя оценка для первой частоты по Донкерлея получена в [26] и имеет вид:

^U D = ^h

EF (n — 1)( n — 2)

\ m(Ca ³ + C ₂ c ³ + C₃bh ²)

Здесь коэффициенты также найдены как общие члены последовательностей решений в системе Maple:

C 1 = (8 n ⁶ - 88 n ⁵ + 473 n ⁴ - 1300 n ³ + 1861 n ² - 1318 n + 360) / 24,

C ₂ = (5 n ⁴ - 25 n ³ + 62 n ² - 73 n + 30) /12,

C ₃ = 2(4 n - 3)(8 n ³ - 48 n ² + 104 n - 77) / (3( n - 2)).

С таким же успехом для обобщения решений на произвольное число панелей можно воспользоваться системой компьютерной математики Mathematica [15,27].

Из формулы (16) и (17) видно, что структура оценки Донкерлея совпадает с формулой Рэлея, полученной энергетическим методом. Однако формула (17) намного проще, все коэффициенты, найденные индуктивным методом, содержатся только в знаменателе.

• 3    Результаты и их обсуждение / Results and Discussion

Для оценки погрешности найденных аналитических оценок можно использовать численное решение для первой частоты, найденное из всего спектра частот собственных колебаний ферм. Рассматриваемая ферма имеет следующие размеры: а = 3м, h = 1м, h ₂ =3. Площадь поперечных сечений стержней решетки и опорных стержней принимается одинаковой: F = 1см² .

Модуль упругости стали E = 2,1-105MПa, массы в узлах m =150кг. На рисунке 2 представлены зависимость от количества панелей верхней оценки наименьшей частоты гоR по формуле Рэлея (16), частоты гоD по формуле Донкерлея (17) и значения первой частоты го1 спектра системы с K степенями свободы, найденная численно.

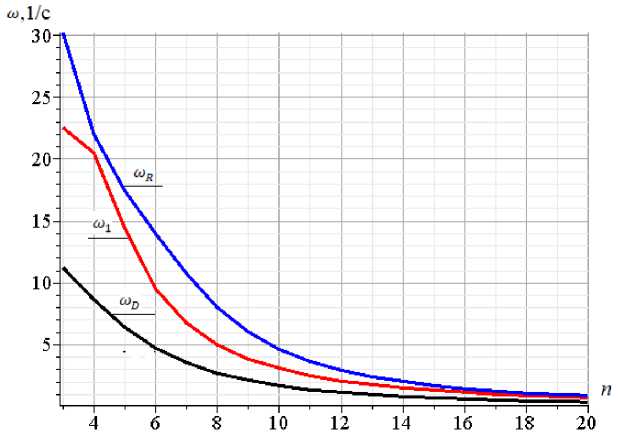
Рис. 2 – Зависимость от количества панелей первой частоты колебаний ω _R по методу Рэлея, частоты ω _D по методу Донкерлея и первой частотой ω ₁ спектра

Fig. 2 – Dependence on the number of panels of the first oscillation frequency ω _R according to the

Rayleigh method, the frequency ω _D according to the Dunkerley method and the first frequency ω ₁ of the spectrum

Из графика на рисунке 2 видно, что с увеличением количества панелей, первая собственная частота монотонно уменьшается. Когда количество панелей невелико (например, n <  8 ), собственная частота уменьшается очень быстро по мере увеличения количества панелей. Погрешность аналитической оценки, как правило, невелика и уменьшается с увеличением числа панелей в ферме. Отсюда можно сделать вывод, что полученное аналитическое решение лучше всего подходит для решения задач с фермами с большим количеством панелей.

Частоты ω _R и ω _D , полученные методом Рэлея и методом Донкерлея значительно отличаются друг от друга. Вероятно, это связано с тем, что 1-я форма колебаний плохо согласуется с выбранной для оценки формой прогиба от действия равномерно распределенной узловой нагрузки, которая используется в решении Рэлея.

Ошибка собственной частоты, полученная методом Донкерлея, намного больше, чем погрешность метода Рэлея. Для уточнения величины оценки полученных приближений можно ввести значение относительной ошибки ε _D = | ω _D -ω ₁|/ ω ₁ , ε _R = | ω _R -ω ₁|/ ω ₁ . На рисунке 3 видно, что погрешность метода Рэлея при некоторых значениях n даже превышает погрешность метода Донкерлея, но с увеличением порядка фермы все-таки резко падает и принимает приемлемые значения около 22%, в то время как погрешность по Донкерлею растет, хотя и незначительно.

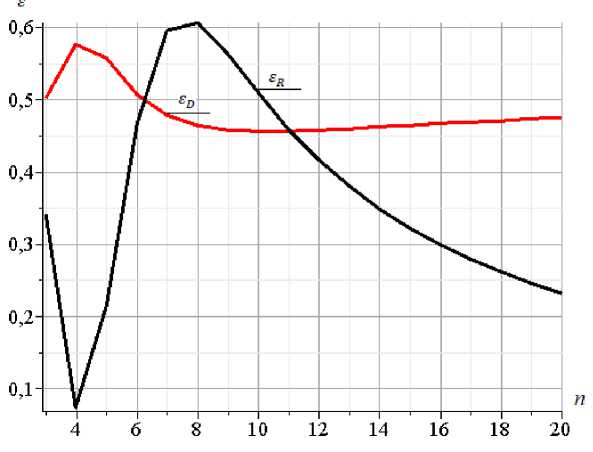
Рис.3 - Относительная погрешность оценки частоты колебаний по Донкерлею £ D и по Рэлею £ R .

Fig.3 - Relative error in estimating the oscillation frequency £ D according to Dunkerley and Rayleigh £ _R .

3.1    Спектры собственных частот регулярных ферм

Более высокие частоты колебаний обычно не используются в инженерных расчетах, за исключением, возможно, исследований резонансных случаев. Частота собственных колебаний, вызванная работой различных устройств (станков, вентиляторов и др.), может совпадать с частотой собственных колебаний конструкции. Аналитически рассчитать эти частоты не представляется возможным, но отлаженный математический аппарат в режиме численных расчетов дает интересную картину наборов спектров регулярных систем. На рисунке 4 восемь кривых соединяют точки, соответствующие частотам колебаний ферм порядков n = 3,...,10. Каждая кривая соответствует ферме данного порядка, ординаты точек на ней — частоты. По оси абсцисс показаны номера собственных частот в упорядоченных спектрах. Спектр простейшей фермы при n = 3 содержит K = 12 n - 16 = 20 частот, спектр фермы порядка n = 10 состоит из 104 частот.

Здесь отмечаются некоторые особенности частотного распределения. Для всех спектров характерны значительные скачки частоты. Независимо от порядка ферм всегда 4( n - 1) частоты лежат в области ниже значения 70 c ^{- 1} . Для принятых размеров фермы a = 3м, h = 1м, F = 1см² появляется постоянная для ферм различного порядка частота 70 c ^{- 1} (спектральная константа). Наличие этой закономерности позволяет прогнозировать некоторые частоты ферм с большой регулярностью, по расчету ферме с малым числом панелей, что существенно упрощает решение.

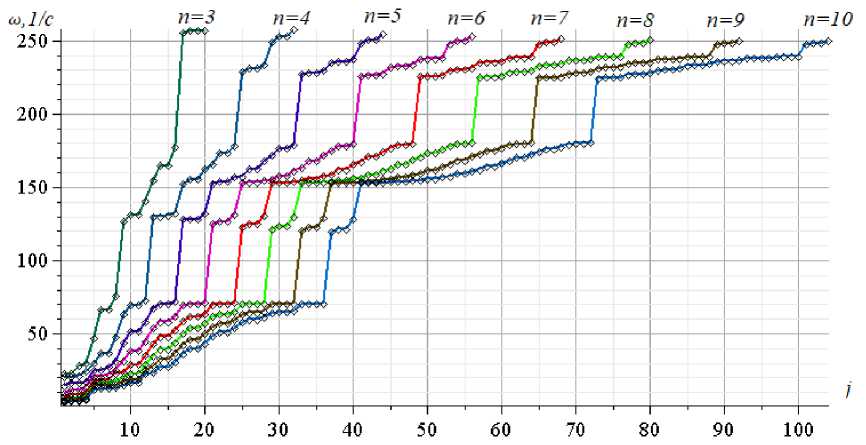
Рис. 4 – Спектры регулярных ферм h=1,0 м

Fig. 4 – Spectra of regular trusses h=1,0 m

На графике 4 видно, что частоты распределены по трем четким областям. Первая область содержит 4( n - 1) частоты. Вторая область также содержит 4( n - 1) частот. При малых n первые четыре частоты второй области можно считать постоянными. Третья область состоит из 4( n - 2) частот. При больших значениях n самые высокие частоты также можно рассматривать как константу.

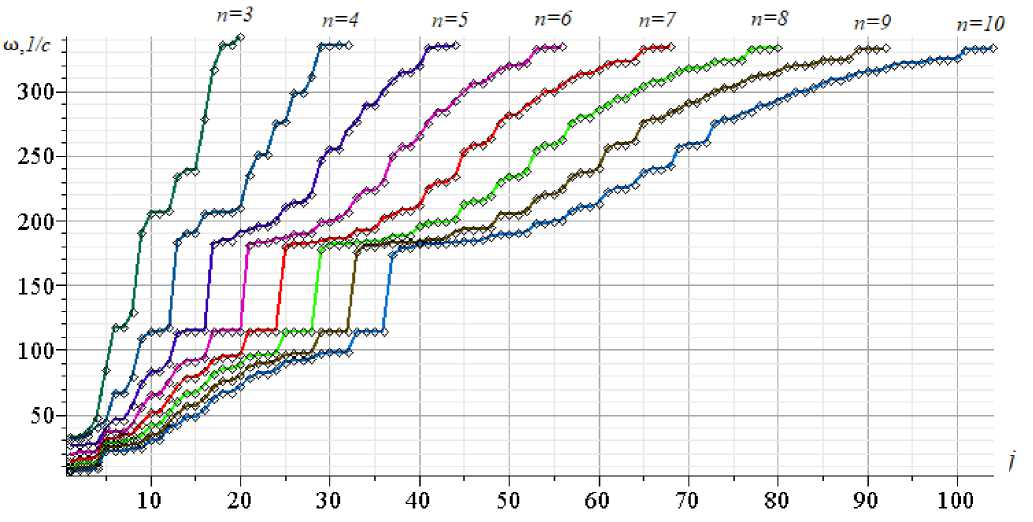
Рис. 5 – Спектры регулярных ферм h =2.0 м

Fig. 5 – Spectra of regular trusses h =2.0 m

Наблюдаемая закономерность не универсальна, а характерна только для определенных значений размеров фермы. Особенно сильно на характер распределения частот в спектрах группы регулярных ферм влияет отношение размеров a / h . Распределение частот в спектрах восьми одинаковых ферм при h = 2,0 м показано на рисунке 5. При размере h = 2,0 картина распределение частот в спектрах имеет только две области. Первая область аналогична частотному распределению на рисунке 4 с постоянной частотой 115 c ^{- 1} . Вторая область с 4(2 n - 3) частотами содержит константу ю = 335 с ^{- 1} .

• 4    Выводы / Conclusions

Основные результаты работы:

• 1.    Рассмотрена схема симметричной статически определимой пространственной конструкции покрытия и получены аналитические зависимости первой частоты колебаний от количества панелей. Найденные расчетные формулы достаточно универсальны и применимы к широкому классу таких конструкций. Алгоритм, использованный при выводе, позволяет просто пересчитать задачу для других типов нагрузок.

• 2.    Аналитические оценки, найденные для наименьшей частоты колебаний, показывают, что точность оценки Рэлея при большом числе панелей достаточна для практического использования, а приближение Донкерлея для принятой модели фермы неудовлетворительна.

• 3.    В спектрах семейства регулярных ферм найдены спектральные константы.

• 5 Финансирование / Fundings

  Работа выполнена при финансовой поддержке РНФ 22-21-00473.