Собственные частоты и собственные формы колебаний нагруженной вращающейся шины

Задача построения быстрых моделей, которые симулируют сложные динамические явления с требуемой точностью и одновременно не выдвигают больших требований к вычислительным ресурсам, актуальна в настоящее время. Одна из таких моделей радиальной шины, позволяющая аналитически проанализировать динамические эффекты, возникающие при качении, была предложена в работах В. Г. Вильке и И. Ф. Кожевникова [1–6]. В этой модели предполагается, что механическая система состоит из двух частей: деформируемой и недеформируемой. Недеформируемой частью колеса является диск 0 , который представляется абсолютно твёрдым телом (рис. 1). Деформируемой частью колеса является шина, поверхность которой состоит из гибкой ленты (бандажа) 3 , контактирующей с опорной поверхностью, и двух боковин 1, 2 , которые соединяют бандаж с диском колеса. При деформациях бандажа, который моделируется в недеформированном состоянии круговым цилиндром радиуса r и высоты 2 l , рассматриваются нелинейные условия нерастяжимо-сти корда (волокна, армирующие бандаж). Боковые поверхности, которые моделируются в недеформированном состоянии частями двух торов, тоже армированы и представляют из себя мембраны. Помимо этого предполагается, что они снабжены материалом, который описывается согласно модели несжимаемой резины Муни–Ривлина. Используя данную аналитическую модель, были исследованы СЧ и СФ колебаний вращающейся нагруженной шины в предположении, что угловая скорость вращения постоянна, а качение по плоскости происходит без проскальзывания.

2.    Модель колеса с армированной шиной

Введём неподвижную систему координат OX1X2X3. Бандаж шины контактирует с опорной плоскостью OX1X2. Начало подвижной системы координат Cx1 x2x3 поместим в центр масс диска точку C с координатами (Xі, X2, X3) в неподвижной системе (рис. 1). Обозначим через li орты осей OXi неподвижной системы координат, а через ei — орты осей Cxi подвижной системы координат. Положение бандажа можно определить двумя поворотами на углы β0 ,θ относительно осей OX3 и Cx2 . Для фиксированных β0 и θ положение точек бандажа определим в виде гз( y,^,t ) = ^Xili +Гз( во)Г2( У)

i =1

Гr e i + 1^ e 2 + r ^ U i ( y,^,t ) e^ ,

	cos ^	0	sin У		cos в о	— sin в о	0
Г 2 ( ^ ) =	0	1	0	,   Г 3 ( в о ) =	sin в о	cos в о	0
	— sin У	0	cos У		0	0	1

где У = Ө+у; параметр £ E [—1; 1], при этом значение параметра £ = 1 (£ = — 1) соответствует линии соединения бандажа с первой (второй) боковиной, значение £ = 0 соответствует срединной линии бандажа 1 о; rUi(у, ^, t) — координаты вектора перемещения точки банда- жа в подвижной цилиндрической системе координат.

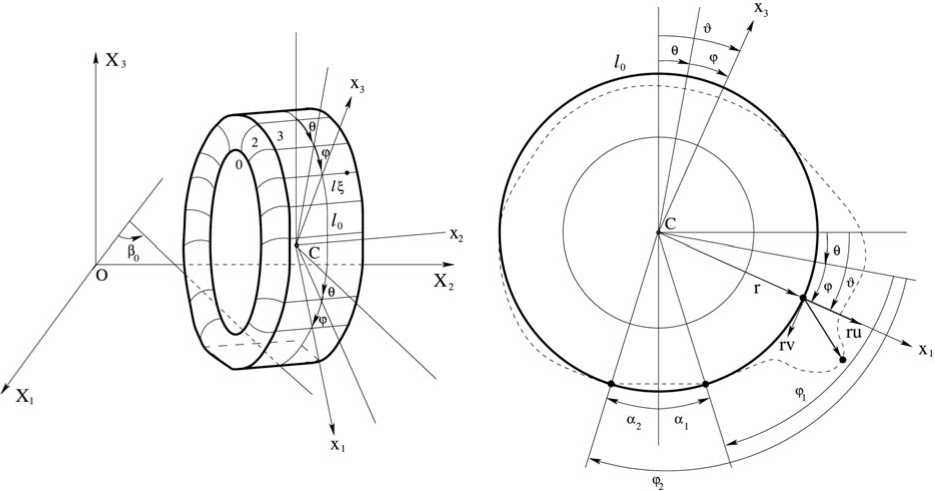
Рис. 1. Модель колеса с армированной шиной

Используя нелинейные условия нерастяжимости волокон, армирующих бандаж, получаются следующие соотношения:

U1 = и (y,t), U2 = w (t), U3 = —v (y,t), выражающие зависимость функций Uk от радиальной ru, касательной rv (рис. 1) и боковой rw компонент вектора перемещений ru(у, t)ei + rw(t)e2 — rv(y,t)ез точек 1 о в подвижной системе координат Cx1x2x3 . Данные соотношения показывают, что круговой цилиндр (недеформированное состояние) трансформируется в цилиндрическую поверхность (деформированное состояние) с образующей, заданной плоской деформированной линией l0, и семейством ортогональных ей прямых. Линия l0 при этом нерастяжима:

2( и + v ) + ( и + v ) ² + ( v — и ' ) ² = 0 , ' = ^д-.

∂ϕ

Область контакта бандажа с опорнойплоскостью OX 1 X 2 представляется прямоугольником постоянной ширины 2 1 и переменной длины, определяемой двумя функциями у i ( t ) ,у 2 ( t ) (рис. 1). Особенность состоит в том, что данные функции неизвестны заранее, и их нужно определить из уравнений движения. Не ограничивая общности, можно предположить, что линия 1 о совпадает с осью OX i (это означает, что угол в 0 = 0). Таким образом, можно определить перемещения точек 1 о в зоне контакта L i = [ у i ( t ) , у 2 ( t )]. Будем также считать, что X 2 = 0 и, следовательно, w = 0, что означает, что центр масс диска не смещается вбок. Пусть колесо катится без проскальзывания и без подпрыгивания. Это означает, что скорости точек l 0 в зоне контакта L 1 равны нулю. Применим вариационный принцип Гамильтона–Остроградского:

t 2

J (ST + 5A )d t = 0, t1

где кинетическая энергия колеса T представляет из себя сумму кинетической энергии абсолютно жесткого диска и кинетической энергии деформированной шины. Вся масса шины сосредоточена в линии l 0 с линейной плотностью ρ . Работа сил δA на возможных перемещениях имеет сложную структуру:

SA = SA F + A + SN 1 + SN 3 + SN 6 .

Здесь δA F — работа продольной силы, вертикальной нагрузки и крутящего момента, приложенных к диску колеса, работа δA P — работа потенциальных сил (работа давления на возможных перемещениях и вариация потенциальной энергии растяжения резины), работы δN 1 , δN 3 — работы реакций связей (движение без проскальзывания, без подпрыгивания в зоне контакта), работа δN 6 — тоже работа реакции связи (условие нерастяжимости срединной линии бандажа), имеющая следующую структуру:

SN 6 = jА ( у, t ) ( (1 + u + v ' )( Su + Sv ) + ( U — v )( Su' — Sv ) ) d у,

L 2

где L 2 = [ у 2 ( t ) , 2 п + у i ( t )] описывает свободную поверхность шины, множитель Лагранжа А = А ( у, t ) определяет натяжение 1 о . В результате применения вариационного принципа получается система четырнадцати уравнений движения, которая имеет следующую структуру: три уравнения Лагранжа второго рода с неопределёнными множителями (особенность уравнений — наличие интегральных членов от функций u , v и их производных), четыре уравнения движения в частных производных, три уравнения связей и четыре динамических граничных условия. При нахождении u , v также необходимо учесть кинематические граничные условия.

3.    Малые колебания шины

Теперь поставим задачу о малых колебаниях шины в окрестности стационарного режима. Пусть угловая скорость вращения колеса Q постоянна, тогда

X _i = r Q , X ₃ = const , Ө = Q .

Перейдём от переменной у к переменной а = у + fit — п/ 2, тем самым осуществив переход от лагранжева описания к эйлеровому. Функции, определяющие деформации линии l 0 , зону контакта и множитель Лагранжа представим в следующем виде:

и (у^) = U (а) + Uvib(а,t), v (у,t) = V (а) + Vzib(а,t), А (у,t) = А° (а) + А vib(а,t), ак (t ) = ак+а vib k (t), а°. = ук (t )+Q t — П = const, у? k (t) = — Q, где первая часть U (а), V (а), А ° (а), а° функций описывает стационарный режим качения без проскальзывания, а вторая часть Uvib(а,t), VVib(а,t), Аvib(а,t), аvib°(t) функций описывает колебания в окрестности этого стационарного режима. Теперь границы зоны контакта описываются функциями ai(t), а2(t) (рис. 1). Функция Vvib удовлетворяет следующему уравнению и граничным условиям:

pr 3 V ib - pr ³ V vib + 2 pr ³ Q V v³) + 2 pr ³ Q V i_b + a о V ^t) + a i V ^ + a 2 V vib = 0 ,

V vib ^{( a} 1 ^{+2 n} + ^a vib1 ⁾⁼⁰ , V vib ^{( a} 1 +^{2 n + a} vib1 ⁾⁼⁰ , V vib ^{( a} 2 ^{+ a} vib2 )=⁰ , V vib ^{( a} ◦ ^{+ a} vib 2 ⁾⁼⁰ •

Здесь a 0 , a 1 , a 2 — постоянные коэффициенты, которые зависят от геометрии шины и внутреннего давления. При нахождении СЧ колебаний зону контакта можно считать постоянной, тогда граничные условия в (1) заменяются следующими соотношениями:

V vib ^{( a} l ^{+2 n ) +} V Hb ^{( a} 1 ^{+2 n} ) ^a vib 1 ~ V vib ^{( a} 1 ^{+ 2 n )=0} , V vib ^{( a} 2 ^{) +} V v ib ^{( a} 2 ) ^a vib 2 ~ V vib ^{( a} 2 ⁾⁼⁰ ,

V vib ^{( a} l ^{+2 n ) +} V vb ^{( a} 1 ^{+2 n} ) ^a vib 1 ~ V v ib ^{( a} 1 ^{+ 2 п} )=⁰ , V vib ^{( a} 2 ^{) +} V v i b ^{( a} 2 ) ^a vib 2 ~ V vib ^{( a} 2 )=⁰ •

Для упрощения записи в дальнейшем будем использовать а к вместо а к . Используя метод разделения переменных (метод Фурье), представим

V vib ( a,t ) = e i А ( a ) •                                    (2)

Здесь ω — это циклическая частота. Подставив данное выражение в (1), получим a о X(4) + 2 pr 3Q ш i X(3) + (a i - pr 3 ш 2) X " + 2 pr 3Q ш i X' + (a 2 + pr 3 ш 2) X = 0 •

Решение данного уравнения имеет следующую структуру:

X (a) = G iep1 а + G 2ep2 a + G 3ep3 a + Gtep4 a, где коэффициенты p1 , p2, p3, p4 удовлетворяют характеристическому уравнению четвертой степени:

a 0 p4 + 2 pr3 Q ш ip3 + (a 1 — pr3 ш 2) p2 + 2 pr 3Q ш ip + (a 2 + pr3 ш 2) = 0, которое решается методом Феррари, а коэффициенты G1, G2, G3, G4 определяются, в свою очередь, из граничных условий:

G _{i e} p i ^{( a} i +^{2 n} ) + G ₂ e p 2 ^{( a} i +^{2 n} ) + G 3 _e ^p з ^{( a} i +^{2 n} ) + G ₄ e p 4 ^{( a} 1 ^{+2 n} ) = 0

G i e p ^{1 a 2} + G 2 e ^{p 2 a 2} + G 3 e p ^{3 a 2} + G t e p ^{4 a 2} = 0 ,

G _i p _i e ^{p 1 ( a 1 +2 n} ) + G ₂ p ₂ e ^p 2 ^{( a 1 +2 n} ) + G ₃ p ₃ e p 3 ^{( a 1 +2 n} ) + G ₄ p ₄ e p 4 ^{( a 1 +2 n} ) = 0 ,

G i p i e p ^{1 a 2} + G 2 p 2 e ^{p 2 a 2} + G 3 p 3 e p ^{3 a 2} + G 4 p 4 e p ^{4 a 2} = 0

в виде

G i = e ^{- p 1 ( a 1 +2 n} ) ( ( p 4 — p 3 )e p ^{2 (a a - 2 n} ) — ( p 4 — p 2 )e ^p 3 ^{(A a - 2 n} ) + ( p 3 — p 2 )e ^p 4 ^{(A a - 2 n} ) ) G 5 ,

G 2 = e ^{- p 2 ( a 1 +2 n} ) ( — ( p 4 — p 3 )e ^{p 1 (A a - 2 n} ) + ( p 4 — p i )e p 3 ^{(A a - 2 n} ) — ( p 3 — p i )e p 4 ^{(A a - 2 n} ) ) G 5 ,

G ₃ = e ^{- p 3 ( a 1 +2 n} ) ( ( p ₄ — p ₂ )e p ^{1 (A a - 2 n} ) — ( p ₄ — p _i )e ^p 2 ^{(A a - 2 n} ) + ( p ₂ — p _i )e ^p 4 ^{(A a - 2 n} )) G 5 ,

G4 = e-p4(a 1+2n) (— (p3 — p2)ep 1(Aa-2n) + (p3 — pi)ep2(Aa-2n) — (p2 — pi)ep3(Aa-2n)) G5, где G^ — произвольная константа. Однородная система (3) имеет ненулевое решение, если её определитель равен нулю:

f ( _ш ) = _e ( P 1 + P 2 + P 3 + P 4 ^{)( a} 1 +^{2 n} ) [( p 3 _— p 1 )( p 4 _— p 2 ) (e ( P 2 + P 4 ^{)(A a - 2 n} ) + _e ( P 1 + P 3 ^{)(A a - 2 n} )) ( p 3 - p 2 )( p 4 - p 1 ) ( e ^{( P 1 + P 4 )(A a - 2 n} ) +e ^{( P 2 + P 3 )(A a - 2 n} ) )

-

-

-

-

( Р 2 - Р 1 )( Р 4 - Р з ) (e ^{( P 3 +} p 4 ^{)(A a - 2 n} ) +e ⁽ p ^{1 +} p 2 ^{)(A a - 2 n} ))]

-

= 0 .

Здесь A a = a 2 — a 1 . Таким образом, мы получили частотное уравнение (5), из которого и определяются СЧ: v = ш/ (2 п ). Если по оси абсцисс отложить угловую скорость вращения колеса Q, а по оси ординат отложить значения СЧ, соответствующих данной угловой скорости, то получится график зависимости СЧ от угловой скорости. Пример такого графика представлен на рис. 2 для A a = 0 . 3 рад. Можно заметить, что при увеличении угловой скорости СЧ убывают. Также на рис. 2 представлено увеличение области частот в окрестности 100 Гц, где можно увидеть любопытный эффект «разбегания» частот.

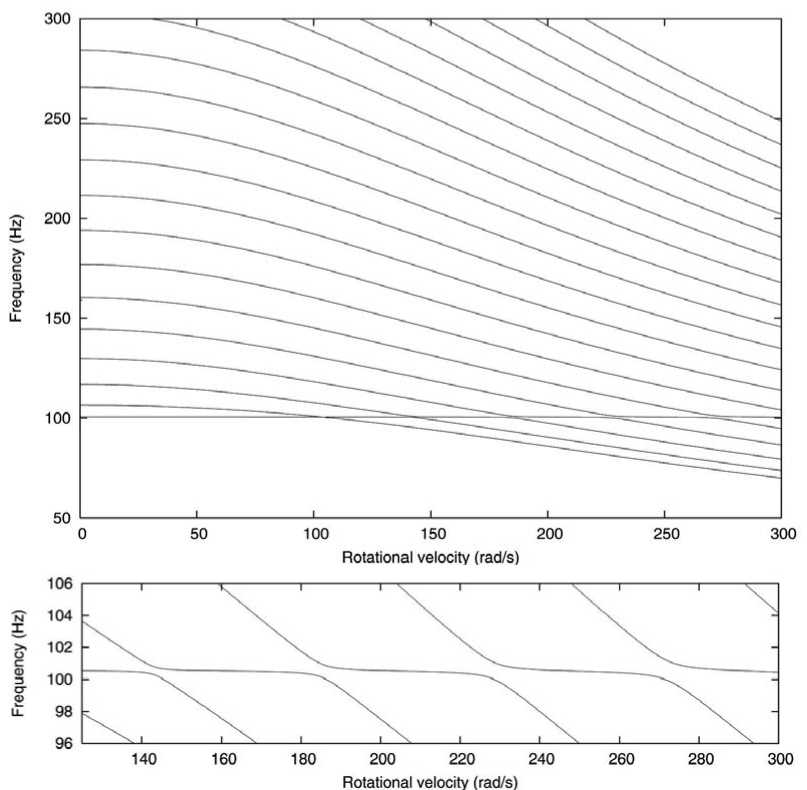
Рис. 2. СЧ как функции угловой скорости вращения для A a = 0 . 3 рад

Что касается СФ, то, зная СЧ, по аналитическим формулам вычисляются p і ( ш ), p 2 ( ш ), p з ( ш ), p ₄ ( ш ) и, следовательно, по формулам (4) коэффициенты G 1 , G ₂ , G 3 , G ₄ . Если соотношение (2) переписать в виде

Vvib(a,t)= (cos(шt)Re(X(a)) — sin(шt)Im(X(a)/)+i (cos(шt)Im(X(a))+sin(шt)Re(X(a))^ , тогда вначале покажется странным, что добавка У^ь(a,t), связанная с колебаниями, к касательной составляющей вектора перемещений имеет действительную и мнимую части. Но на самом деле мнимая СФ Im(X(а)) переходит в действительную СФ Re(X(а)) и наоборот:

V vib ( а, 0) = Re( X ( а )) +iIm( X ( а )) ,

V vib ( а, £) = “ Im( X ( а )) +iRe( X ( а )) ,

что означает, что есть только одна СФ, например Re( X ( а )), но она поворачивается. В качестве примера на рис. 3 показан поворот второй СФ, отвечающей частоте колебаний 95 Гц, для А а = 0 . 3 рад и угловой скорости вращения диска П = 175 рад • с ~ 1 .

Рис. 3. Колебания на частоте 95 Гц второй СФ нагруженной шины, вращающейся с угловой ско-

ростью П = 175 рад • с ¹ для А а = 0 . 3 рад

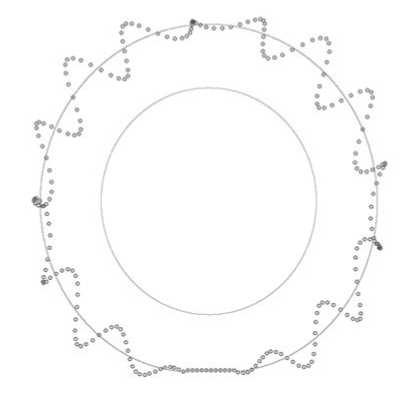
Рис. 4. Траектория движения точки срединной линии бандажа нагруженной вращающейся шины при частоте колебаний 114 Гц и угловой скорости вращения диска П = 50 рад • с ^{_ 1} для А а = 0 . 3 рад

Если перейти в невращающуюся подвижную систему координат с началом в центре масс диска точке C (система Кёнига), то можно в этой системе изобразить (рис. 4) траекторию движения точки срединной линии бандажа, при условии, что угловая скорость вращения диска П = 50 рад • с ~ 1 , а частота колебаний составляет 114 Гц.