Собственные колебания нагретых функционально-градиентных цилиндрических оболочек, содержащих жидкость
Автор: Бочкарев С.А., Лекомцев С.В.
Статья в выпуске: 4, 2015 года.
Бесплатный доступ
Представлены результаты исследований собственных колебаний нагретых круговых цилиндрических оболочек, содержащих неподвижную идеальную жидкость и выполненных из функционально-градиентных материалов. Температурно-зависимые эффективные свойства материала, состоящего из смеси оксида циркония и сплава титана, изменяются по толщине оболочки согласно степенному закону. Распределение температуры по радиальной координате определяется из решения квазилинейного одномерного уравнения теплопроводности. В качестве математической формулировки задачи динамики оболочки используется классическая теория оболочек и принцип возможных перемещений. Поведение жидкости описывается в рамках потенциальной теории. Соответствующее волновое уравнение совместно с условием непроницаемости и граничными условиями преобразуются к системе уравнений с использованием метода Бубнова-Галеркина. В результате решение задачи, осуществляемое с помощью полуаналитического варианта метода конечных элементов, сводится к вычислению комплексных собственных значений связанной системы уравнений. Достоверность результатов, получаемых в рамках разработанного алгоритма, оценена путем сравнения с известными численно-аналитическими решениями. Для круговых цилиндрических оболочек с различными вариантами граничных условий продемонстрированы зависимости минимальных частот колебаний от температурной нагрузки при разных консистенциях функционально-градиентного материала. Определены критические значения температур при разных условиях нагрева и геометрических размерах. Проанализировано различие, оказываемое нагревом на динамические свойства пустых оболочек и оболочек, взаимодействующих с жидкостью. Показано, что наличие жидкости внутри оболочки проявляет наиболее существенное влияние на колебательные характеристики нагретых консольно закрепленных оболочек.
Цилиндрическая оболочка, функционально-градиентный материал, температурное нагружение, потенциальная жидкость, метод конечных элементов, собственные колебания
Короткий адрес: https://sciup.org/146211584
IDR: 146211584 | УДК: 539.3 | DOI: 10.15593/perm.mech/2015.4.02
Текст научной статьи Собственные колебания нагретых функционально-градиентных цилиндрических оболочек, содержащих жидкость
При всем многообразии численно-аналитических и численных работ, посвященных исследованию конструкций, выполненных из функционально-градиентных (ФГ) материалов [1], только в незначительном числе статей затрагиваются вопросы их взаимодействия с газообразной [2-6], а также неподвижной [7-10] или текущей [11-13] жидкой средой. Такой ограниченный список источников не является очевидным, поскольку высокие жаропрочные свойства, обусловленные использованием керамики в качестве одного из составляющих, подразумевают применение ФГ-материалов в авиационной и ракетной технике, где упругие конструкции взаимодействуют с нагретым потоком жидкости или газа. Только в некоторых из вышеперечисленных работ учитывается температурное нагружение, а свойства материала принимаются зависимыми от температуры. Однако для упрощения используется постановка, в которой коэффициенты теплопроводности не зависят от температуры. Такое допущение позволяет использовать аналитическое выражение для нахождения распределения температуры по толщине оболочки. Более точная формулировка требует непосредственного численного решения квазилинейного уравнения теплопроводности. Несмотря на то, что получаемые результаты достовернее описывают поведение реальных машиностроительных конструкций, этот подход распространен в меньшей степени [14-17].
Ни в одной из указанных работ, где рассматриваются ФГ-оболочки, содержащие неподвижную жидкость, не принимаются во внимание температурные нагрузки. Влияние различных параметров на собственные частоты колебаний свободно опертых ФГ-обо-лочек с жидкостью исследовалось в [7] при помощи трехмерных уравнений теории упругости. В работе [8] оценено влияние различных комбинаций граничных условий на собственные частоты колебаний оболочки, заполненной жидкостью и выполненной из стали и никеля. Аналогичный подход используется в [9] для анализа расположенной на упругом основании оболочки с жидкостью. Представленные в этих статьях численно-аналитические решения применимы лишь к цилиндрическим оболочкам, содержащим несжимаемую жидкость, потому что гидродинамическое давление вычисляется с помощью аналитического выражения, записанного относительно функций Бесселя. Более общая формулировка, основанная на использовании метода конечных элементов, предложена в работе [10]. Здесь исследовалось влияние различных комбинаций граничных условий на собственные частоты колебаний оболочек с различными геометрическими размерами. Таким образом, влияние температурной нагрузки на спектр собственных частот цилиндрических оболочек, содержащих неподвижную жидкость, остается не изученным. В связи с этим нашей целью является проведение такого анализа при различных комбинациях кинематических граничных условий. Моделирование жидкости осуществляется в рамках потенциальной теории, согласно которой единственной искомой величиной является потенциал скорости. В результате решение задачи сводится к вычислению комплексных собственных значений несимметричной матрицы. Отметим, что незначительная модификация алгоритма позволяет учитывать как течение, так и вращение невязкой сжимаемой жидкости или газа [18-19].
1. Постановка задачи и основные соотношения
Рассматривается выполненная из функционально-градиентного материала упругая цилиндрическая оболочка (рис. 1) длиной L и радиусом R , внутри которой находится идеальная сжимаемая жидкость плотностью р f . Одна поверхность оболочки, например наружная, нагревается до заданной температуры To , тогда как температура другой всегда остается равной T = 300 K. Целью работы является исследование влияния свойств ФГ-материала на собственные колебания нагретой оболочки при различных вариантах кинематических граничных условий и линейных размерах конструкции.
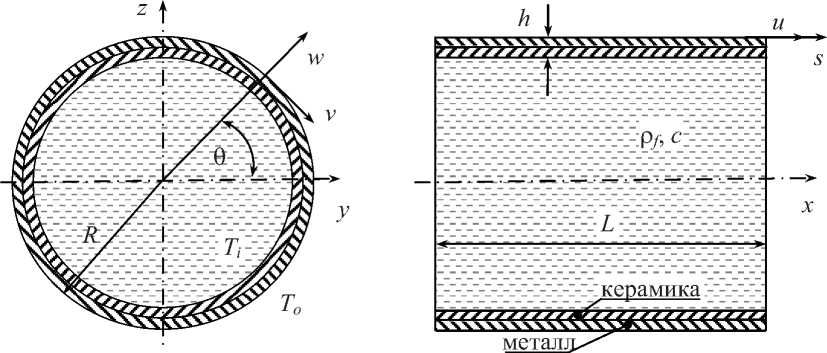
Рис. 1. Содержащая жидкость цилиндрическая оболочка, выполненная из функционально-градиентного материала
Для описания неподвижной жидкости в области V f вводится в рассмотрение потенциал скорости ф, который в цилиндрической системе координат ( r , 0, x ) в случае малых возмущений описывается волновым уравнением [20]
V2 n = a2- । 1 ^+-^+1 У^ = 1 52ф m
- a r 2 r 2 ao 2 a x2 r a r c2 a t2 ’ 1
где с - скорость звука в жидкости. Давление жидкости р на упругую конструкцию вычисляется по линеаризованной формуле Бернулли
P f = -р f а^- на поверхности S с = S f П S s .
Здесь ^ - меридиональная координата оболочки; Sf, Ss - площади, ограничивающие объемы жидкости и оболочки соответственно. На поверхности раздела оболочка-жидкость Sа задается условие непроницаемости а- _ aw an at ’
где n - нормаль к поверхности; w - нормальная составляющая вектора перемещений оболочки. Потенциал скорости подчиняется следующим граничным условиям:
x = 0: - = 0, x = L : a-/a x = 0.
Для дальнейшей численной реализации задачи на основе полуаналитического варианта метода конечных элементов (МКЭ) дифференциальное уравнение для потенциала скорости (1) с граничными условиями (3) и (4) преобразуются с помощью метода Бубно-ва-Галеркина [18].
Компоненты вектора деформации в криволинейной системе координат ( s , 0, z ) определяются с помощью классической теории оболочек, основанной на гипотезах Кирхгофа-Лява. Для эквидистантной поверхности они могут быть записаны следующим образом [21]:
8 11 = Е 11 + zk 11 ,
= Е 22 + zk 22 ,
= Е 12 + zk 12 ,
где
Е 11 =8 1 +1/20 2 , k n = к 1 , ( 1 ^2 ) , Е 12 = 8 12 + 0 1 0 2 , k 12 = 2т
и a и
81 = , as
82 =
1 [av ]
+ w , r (ao у
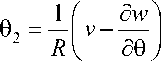
a 2 w
kг
a v 1 a и
=--1--- as r ao
'a v a 2 w
r 2 (ao ao2
A - a w
01 "-ls •
т=[^ -a^w ^
r (as asaoJ
Здесь и , v - меридиональная и окружная составляющие вектора перемещений; o i - углы поворота недеформируемой нормали.
Компоненты деформаций срединной поверхности (5) в матричной форме можно представить в виде
£ = £* +1/2 Ее, где £ = {Е119Е22,Е12,ku,k22,k12}T, £* ={s15e2,e12,k1,k2,2т}Т - линейная часть деформации, е = {0,0,0,0,01,62,0,0,0}Т; Е - матрица линейных множителей, которая имеет ненулевые компоненты Е15 = 01, Е16 = 02, Е35 = 02, Е36 = 01.
Физические соотношения, устанавливающие связь между вектором усилий и моментов T = { T„, T 22 , T 2 , M ,1 , M 22 , M , 2}T и вектором деформаций e , запишем в матричном виде:
" th
A
B
B
C
e
T
\ M th
где T th = { T 1 , T 22,0 } Т и M th = { M h M /. .0/
векторы температурных усилий и момен
тов. Коэффициенты, входящие в матрицу жесткостей D, и температурные компоненты определяются как
( a ij , b y , c ij ) = j ( 1, z , z 2 ) Q ij dz , ( i , j = 1,2,3) , (7)
h
( T * , M f ) = f ( 1, z ) Q a A Tdz , « = { a „ ( z , T ) , a » ( z , T ) ,0 }\ (8)
h где
6 11 = Q 22 = E g ( z , T ) / [ 1 -v f ( z , T ) ] , Q 2 = e 2 1 = v f ( z , T ) Q 11 ,
6 33 = E f ( z , T ) /2/ [ 1 + v » ( z , T ) ] .
Здесь A T - перепад температуры относительно значения, не приводящего к появлению начальных напряжений (300 K); h - толщина оболочки; E ef ( z , T ) , v ef ( z , T ) , a eg ( z , T ) -эффективные модуль упругости, коэффициенты Пуассона и температурного расширения материала. Для ФГ-материала эти характеристики определяются свойствами составляющих его материалов P и их объемными долями V . В случае функционально-градиентного материала, представляющего собой смесь металла m и керамики c [22],
P eff = P m V m + P c V c .
В случае оболочки постоянной толщины объемные доли являются функциями радиальной координаты z , отсчитываемой от срединной поверхности, и изменяются согласно степенному закону
= f 2 z + h А =
, c ГНС
V 2 h )
где N - показатель объемной доли, изменяющийся от нуля до бесконечности. С учетом последнего представления эффективные характеристики, под которыми, помимо перечисленных выше, понимаются также плотность материала р ef. ( z , T ) и коэффициент теплопроводности k ef ( z , T ) , вычисляются следующим образом:
N
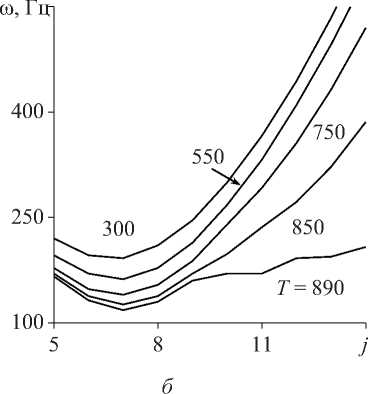
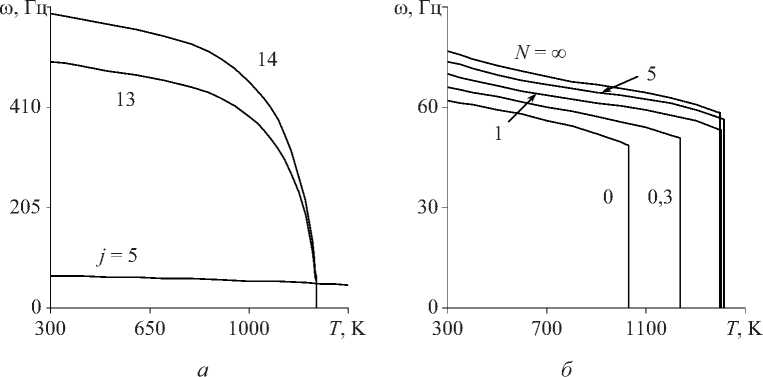
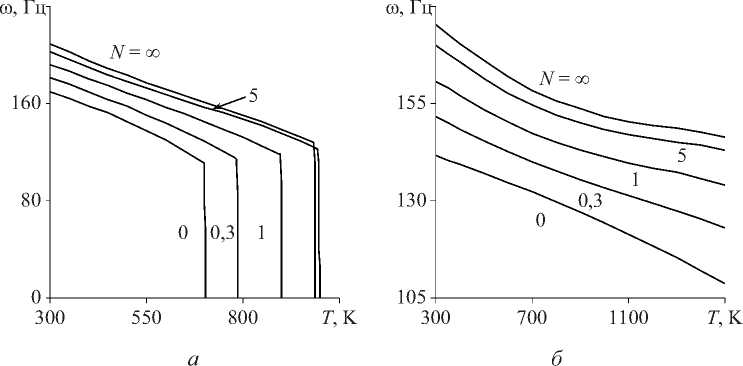
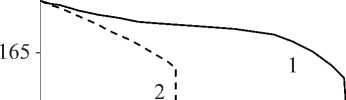
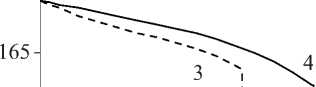
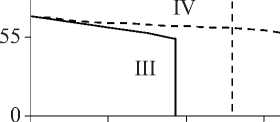
Pf ( Z, T) = Pm Температурно-зависимые свойства материала определяются как P(T) = P (PT-1 +1 + PT + PT2 + PT3). 3 Здесь P), P-1, P1, P2- P3 - коэффициенты температуры T, уникальные для каждого материала. Распределение температуры по толщине оболочки находится из численного решения квазилинейного уравнения установившейся теплопроводности с соответствующими граничными условиями t,T\dL . keff ( Z, T) , dz dz d = 0- T |z=-h/2 = T , T\z=h/2 = To . (9) Для математической формулировки задачи используется принцип возможных перемещений. С дополнительным слагаемым, учитывающим предварительное нагружение, его можно представить в матричной форме [23]: J 8eTDe,dS + J 8dTp0ddS + J 8eTo0edS - J 8dTPdS = 0. (10) SSSS Здесь d и P = {o 0 Pf } - векторы обобщенных перемещений и поверхностных нагрузок, p0=JAPf (z, T) dz . Матрица о0, элементы которой находятся из условия ETDe*0 = о0e, имеет следующие ненулевые компоненты: а^ = T11, а^ = T22. Здесь верхний индекс «0» означает начальное равновесное состояние, а усилия Tii вычисляются по формуле (6). 2. Численная реализация Численное решение задачи осуществляется с использованием полуаналитического варианта МКЭ [24], основанного на представлении решения в виде ряда Фурье по окружной координате 6: (u,w,ф)=Ц°=0(uj, wj,фj)cos j6, vZ'=0vjsin j6, где j - номер гармоники. Выражая в (11) искомые переменные через их узловые значения, получим для произвольных конечных элементов оболочки и жидкости U = { u, v, w}T = Nde,(12) Ф = Ffe, где N и F - матрицы функций формы оболочечного конечного элемента и потенциала скорости; de и fe - векторы узловых значений. Для оболочек используется конечный элемент в виде усеченного конуса с аппроксимацией меридиональной и окружной компонент вектора перемещений линейным полиномом, а нормальной компоненты - кубическим полиномом. Для жидкости применяется треугольный конечный элемент с линейной аппроксимацией потенциала скорости. С учетом (12) e* = Bde, e = Gde, где B и G - матрицы связи деформаций e* и e с узловыми значениями. Применяя стандартные процедуры МКЭ, получим из преобразованного волнового уравнения для потенциала скорости и принципа возможных перемещений (10) с учетом (12)-(14) связанную систему двух уравнений. Ее можно записать в матричном виде, представляя возмущенное движение оболочки и жидкости как (d, ф) = (q, f ) exp(i*юt). ( K -to2M + i *юС ){q, f }T = 0, + K g 0 M, 0 K f 0 0 C = M f J, [c fs Csf Ks = ^J BT DBdS, Ms = ^J NT p0N dS, M f =^J -1 FTFdV, ms Ss ms Ss mf Vf C K f = Zf < BFT BF 1 BFT BF BFT BF mf Vf V Вr Br r2 BO BO Bx Bx C„ = P f Zf NT FdS, K ms S„ dV, Cfs =-Zf F T NdS, ms S„ g = Zf G T o°G dS. ms Ss Здесь mf и ms - число конечных элементов, на которые разбиваются области жидкости и оболочки; N - матрица функций формы нормальной составляющей вектора перемещения оболочки; ю - характеристический показатель, в общем случае являющийся комплексным; i * = V—1 . Таким образом, задача о свободных колебаниях нагретой цилиндрической ФГ-оболочки, содержащей неподвижную жидкость, сводится к выполнению следующей последовательности шагов: • из решения квазилинейного уравнения (9) определяется распределение температуры по толщине оболочки A T (z) при заданных граничных условиях на внутренней Ti и наружной To поверхностях. Соответствующий алгоритм подробно описан в [14]; • на основе полученного распределения температуры по толщине оболочки вычисляется вектор температурных усилий и моментов Tth; • из решения осесимметричной статической задачи Ksd = P0 , где P0 = BTT thdS, Ss по формуле (6) формируются компоненты матрицы начальных усилий и моментов о0; • в результате применения итерационного алгоритма на основе метода Мюллера [25], из решения системы (15) определяются и анализируются собственные частоты ю. В численных примерах рассматривается цилиндрическая функционально-градиентная оболочка (h = 1 х 10-3 м), выполненная из оксида циркония и сплава титана. Физикомеханические характеристики составляющих материалов приведены в табл. 1. Расчеты выполнялись для нескольких конфигураций (табл. 2), в которых чередуются базовые материалы и условия нагрева на внутренней и наружной поверхностях оболочки. Вычисле- ния осуществлялись для оболочек, один край которых всегда жестко закреплен (u = v = w = Sw/Ss = 0, C). На другом краю задаются следующие граничные условия: свободное опирание (v = w = 0, S), жесткое закрепление, свободный край (F). Численными экспериментами было установлено, что для достижения приемлемой точности вычислений достаточно 40 оболочечных конечных элементов и 1000 элементов для жидкости. Таблица 1 Физико-механические свойства составляющих материалов и их зависимость от температуры Свойства P 0 P-1 P1 P 2 P 3 Оксид циркония, ZrO2 [26] р, кг/м3 5,7000х103 0 0 0 0 E, Па 2,4427х10п 0 -1,3707х10-3 1,2139х10-6 -3,6814х10-10 V 0,2882 0 1,1335х10-4 0 0 a, 1/К 1,2766х10-5 0 -1,4900х10-3 1,0х10-6 -0,6775х10-11 к, Вт/мК 1,7 0 1,2760х10-4 6,6485 х10-6 0 Сплав титана, Ti-6Al-4V [26] р, кг/м3 4,4290х103 0 0 0 0 E, Па 1,2256x1011 0 -4,5864х10-4 0 0 V 0,28838 0 1,1214х10-4 0 0 a, 1ZK 7,5788х10-6 0 6,5000х10-4 3,1467х10-7 0 к, Вт/мК 1,2095 0 1,3938х10-2 0 0 Сталь, SUS304 [8] р, кг/м3 8166 0 0 0 0 E, Па 2,0104x1011 0 3,079х10-4 -6,534х10-7 0 V 0,3262 0 -2,002х10-4 3,797х10-7 0 Никель, [8] р, кг/м3 8900 0 0 0 0 E, Па 2,2395x10й 0 -2,794х10-4 -3,998х10-9 0 V 0,31 0 0 0 0 Таблица 2 Варианты расчетов Конфигурация I Конфигурация II Конфигурация III Конфигурация IV ZrO2 / Ti-6Al-4V нагрев снизу ZrO2 / Ti-6Al-4V нагрев сверху Ti-6Al-4V / ZrO2 нагрев снизу Ti-6Al-4V / ZrO2 нагрев сверху 3.1. Тестирование алгоритма 3.2. Собственные колебания нагретой оболочки без жидкости Тестирование разработанного алгоритма осуществлено путем сравнения с результатами работы [8], в которой собственные частоты колебаний заполненной жидкостью ФГ-оболочки (LZR = 20, RZh = 500) получены волновым методом. Оболочка выполнена из стали (внутренняя поверхность) и никеля (наружная поверхность). Свойства материалов не зависят от температуры и определяются из табл. 1 при 300 K. Сравнение двух низших частот колебаний (Гц) для двух гармоник в случае пустой и заполненной жидкостью цилиндрической оболочки для различных значений показателя объемной доли N и граничных условий представлено в табл. 3. Здесь через m обозначено число полуволн в мери- диональном направлении. В верхней строке приведены данные из [8], а в нижней строке -полученные в настоящей работе. Результаты демонстрируют хорошее совпадение с известными данными, особенно в случае свободно опертых оболочек, где различие не превышает 2 %. Таблица 3 Сравнение собственных частот пустой и содержащей жидкость ФГ-оболочки при различных граничных условиях m j N = 0,3 N = 1 N = 5 Пустая С жидкостью Пустая С жидкостью Пустая С жидкостью Граничные условия SS 1 2 4,4160 4,4159 0,9031 0,9137 4,4737 4,4736 0,9049 0,9155 4,5498 4,5497 0,9076 0,9188 3 4.0940 4,0940 0,9599 0,9656 4,1478 4,1478 0,9620 0,9678 4,2183 4,2183 0,9650 0,9708 2 2 16,628 16,628 3,3988 3,4676 16,848 16,848 3,4062 3,4751 17,132 17,132 3,4158 3,4848 3 8,7166 8,7165 2,0419 2,0929 8,8299 8,8298 2,0462 2,0973 8,9807 8,9805 2,0527 2,1038 Граничные условия CC 1 2 9,5233 9,3979 1,9473 1,9511 9,6487 9,5219 1,9514 1,9553 9,8121 9,6824 1,9569 1,9607 3 5,7422 5,7325 1,3458 1,3682 5,8166 5,8080 1,3486 1,3713 5,9161 5,9065 1,3529 1,3755 2 2 25,549 24,674 5,2189 5,1588 25,888 24,999 5,2303 5,1699 26,325 25,420 5,2448 5,1840 3 12,847 12,653 3,0073 3,0567 13,015 12,818 3,0138 3,0635 13,236 13,036 3,0232 3,0728 Граничные условия CS 1 2 6,7063 6,6459 1,3714 1,3778 6,7943 6,7334 1,3742 1,3808 6,9096 6,8474 1,3782 1,3847 3 4,7475 4,7372 1,1129 1,1238 4,8093 4,7994 1,1153 1,1263 4,8914 4,8810 1,1188 1,1298 2 2 20,873 20,542 4,2651 4,2895 21,149 20,813 4,2744 4,2988 21,506 21,164 4,2864 4,3106 3 10,648 10,578 2,4935 2,5484 10,787 10,716 2,4988 2,5539 10,971 10,898 2,5067 2,5617 Для оценки влияния жидкости на динамические характеристики ФГ-оболочки целесообразно проанализировать влияние температурной нагрузки на собственные частоты колебаний пустой оболочки. Внешнее воздействие повышенной температуры, осуществляемое, например, в результате контакта с горячим потоком жидкости или газа, оказывает дестабилизирующее влияние на упругое тело и может привести к потере устойчивости. В табл. 4 приведены значения минимальной температуры нагрева T (K), при которой низшая частота колебаний оболочки ю становится равной нулю и, следовательно, осуществляется потеря устойчивости дивергентного типа. Здесь представлены данные, соответствующие четырем конфигурациям (см. табл. 3), полученные для двух вариантов граничных условий. Показанные в табл. 4 результаты демонстрируют известные закономерности, имеющие место при исследовании выполненных из ФГ-материалов конструкций. С увеличением показателя объемной доли N критические значения температуры возрастают или, наоборот, уменьшаются, в зависимости от того, на какой поверхности располагается более жесткий материал. В некоторых случаях критические температуры, соответствующие промежуточным значениям N, ограниченны значениями, полученными для чистых составляющих материалов (т. е. для N = 0 и N = да). Таблица 4 Критические значения температуры T (K) в зависимости от объемной доли N для пустых оболочек с различными граничными условиями Конфигурация N = 0 N = 0,3 N = 1 N = 5 N = 10 N = 30 N = да Граничные условия CC I 767,76 850,61 966,23 1079,1 1089,9 1091,6 1089,6 II 771,07 798,34 825,47 956,63 1013,29 1065,5 1095,5 III 1089,3 925,97 821,32 773,14 771,37 770,24 767,84 IV 1096,5 1046,5 972,39 858,28 823,57 791,49 771,77 Граничные условия CF I 1714,7 1814,0 1874,2 1871,3 1858,5 1853,6 1858,2 II 978,23 986,15 1001,4 1134,8 1220,0 1302,1 1346,1 III 1858,6 1798,4 1722,6 1698,9 1716,9 1725,3 1715,4 IV 1347,5 1350,6 1340,4 1216,1 1133,3 1040,9 980,34 Анализ данных табл. 4 позволяет выявить некоторые специфические особенности, обусловленные или комбинацией рассматриваемых материалов, или заданным вариантом граничных условий. Например, для некоторых конфигураций имеется определенный диапазон показателя объемной доли N, на котором критические значения температур превышают значения для чистого материала с наибольшей жесткостью (т.е. керамики). Аналогичные зависимости были получены в [15] при исследовании нагретых пустых конических оболочек в случае нескольких комбинаций материалов, в частности, сталь-нитрид кремния. Возможного объяснения такого нехарактерного поведения предложено не было. Хотя в работе [15], как и в настоящем исследовании, рассматривались материалы, свойства которых зависят от температуры, нетипичные зависимости были получены авторами настоящего исследования и в том случае, когда свойства материалов не зависят от температуры. Более того, подобные особенности наблюдались, если вместо нелинейного распределения температуры по толщине оболочки задавалось линейное или однородное распределения. Дополнительные расчеты показали, что в решениях задачи теплопроводности (9), статической задачи, и в распределении температурных усилий и моментов Tth по толщине оболочки отсутствуют закономерности, которые могли бы однозначно характеризовать ту или иную зависимость. Было установлено, что нехарактерное поведение проявляется в том случае, когда материалы имеют существенно различные по величине коэффициенты температурного расширения (как для двух первых материалов в табл. 2). В случае материалов с близкими значениями такая зависимость отсутствует для любой из возможных конфигураций. Немаловажную роль играют также и непосредственные физико-механические свойства некоторых материалов: значительная жесткость приводит к повышению порога потери устойчивости, а увеличение коэффициента температурного расширения, наоборот, способствует его снижению [15]. В результате объединения этих двух факторов возникают предпосылки для появления некоторых специфических зависи- мостей в изменении критических температур от консистенции ФГ-материала, которые повышают эксплуатационные свойства выполненных из них конструкций. Другой особенностью, отраженной в табл. 4, являются результаты, полученные для консольных оболочек. Для этой комбинации граничных условий изменение стороны нагрева приводит к значительному росту критических температур потери устойчивости. Для рассматриваемых в работе идеализированных условий нагрева, при которых температура на одной из поверхностей остается неизменной, смена нагреваемой поверхности приводит к изменению знака температурных моментов Mth. Если в случае жесткого закрепления это ведет к незначительному изменению критических температур, то для консольного закрепления изменение знака способствует большему раскрытию свободного края оболочки и как результат - существенному снижению порога устойчивости. Из табл. 4 можно также увидеть, что для одного и того же материала в зависимости от того, на какой поверхности он располагается, имеет место незначительное расхождение в критических температурах. Это различие обусловлено тем, что в случае N = да рассматривается конечное значение показателя объемной доли. Поэтому при вычислении жесткостных характеристик, усилий и моментов по формулам (7)-(8) при z - ± И/2 принимаются во внимание свойства другого материала. 3.3. Собственные колебания нагретой оболочки с жидкостью На рис. 2, а для жестко закрепленной ФГ-оболочки, внутри которой содержится неподвижная жидкость (рf = 1000 кг/м3, c = 1500 м/с), представлены зависимости низших частот колебаний ш (Гц) от номера гармоники j, полученные при температуре T = 300 K и различных значениях объемных долей N. Здесь показана уже упомянутая ранее типичная картина, имеющая место при исследовании функционально-градиентного материала, а именно: вибрационные свойства конструкции практически всегда ограничены предельными значениями, полученными для чистых материалов. Кривые частотного спектра, вычисленные с произвольным показателем объемной доли N, располагаются между кривыми, полученными для керамики и металла (N = 0). Таким образом, содержащаяся внутри оболочки жидкость не оказывает качественного влияния на характер динамического поведения конструкций, выполненных из ФГ-материала. Как и в случае пустой оболочки, повышение температуры окружающей среды приводит к снижению собственных частот колебаний конструкций, содержащих жидкость. Это демонстрируется данными, приведенными на рис. 2, б. Здесь для жестко закрепленной ФГ-оболочки (N = 1) показаны зависимости минимальных частот колебаний ш (Гц) от номера гармоники j, полученные при различных значениях температуры T (K) внутренней поверхности. Из представленных данных видно, что последовательное ее повышение приводит к постепенному снижению собственных частот ш до тех пор, пока они резко не обращаются в ноль при определенных гармониках. Более подробно это явление демонстрируется на рис. 3, а. Здесь показано изменение собственной частоты колебаний ш от температуры T (K) для гармоник j = 5, 13 и 14. Из рисунка видно, что частота пятой гармоники является минимальной на достаточно широком диапазоне температур, пока собственные частоты более высоких гармоник не достигнут меньших значений. Это происходит благодаря тому, что они сильнее реагируют на возрастание температуры. Такая зависимость в целом определяет характер изменения собственных частот колебаний от температуры для оболочек с некоторыми комбинациями граничных условий, что демонстрируется результатами, показанными на рис. 3, б и 4. На этих рисунках приведены зависимости минимальных частот колебаний го (Гц) от температуры T (К), полученные для оболочек с жидкостью, при разных вариантах граничных условий. Результаты для оболочек с граничными условиями CF (см. рис. 3, б) и CC (рис. 4, а), вычисленные при различных значениях показателя объемной доли N, демонстрируют резкое снижение частоты при достижении некоторого температурного порога, обусловленного, как показано ранее, изменением гармоники с минимальной частотой колебаний. Отметим, что вне зависимости от граничных условий потеря устойчивости осуществляется при j = 14, тогда как в случае пустых оболочек - при j = 13. Для оболочек с граничными условиями CS (рис. 4, б) рост температуры приводит лишь к незначительному уменьшению частоты и потери устойчивости не происходит. Это обусловлено отсутствием закрепления по осевой координате на правом краю оболочки. Тело имеет возможность свободно расширяться в этом направлении, как и в случае граничных условий CF, что препятствует появлению значительных напряжений, возникающих в случае жесткого закрепления обоих краев. Рис. 2. Зависимости минимальных частот колебаний го от номера гармоники j для жестко закрепленной ФГ-оболочки, содержащей жидкость, при различных температурах T (K); конфигурация I: а - T = 300 K; б - N = 1 Более подробные результаты исследований ФГ-оболочек для двух вариантов граничных условий и различных конфигураций сведены в табл. 5. Представленные здесь критические значения температур T (K), по сравнению с полученными для пустой оболочки данными (табл. 4), позволяют сделать вывод о том, что наличие жидкости внутри конструкции, помимо снижения частотного спектра, может оказывать влияние и на характер зависимости динамических свойств конструкций из ФГ-материала от температуры. В частности, наличие жидкости для некоторых конфигураций приводит к расширению диапазона показателя объемных долей, на котором проявляется нетипичная температурная зависимость (CC, конфигурация I), или даже снижает границы устойчивости, определенные значениями для чистых материалов (CC, III). Рис. 3. Зависимости частот колебаний ю от температуры T для консольной ФГ-оболочки при N = 0,3 (а) и разных значениях показателя объемной доли N (б); конфигурация I Рис. 4. Зависимости минимальных частот колебаний ю от температуры T при разных значениях показателя объемной доли N для ФГ-оболочек с различными граничными условиями; Конфигурация I: а - CC; б - CS Наличие жидкости внутри оболочки оказывает наиболее сильное влияние в случае консольного закрепления. Если для жестко закрепленных оболочек нагрев внешней поверхности приводит к возрастанию критических температур, как для пустых оболочек, так и оболочек с жидкостью, то для консольных оболочек нагрев на разных поверхностях по-разному влияет на критические температуры пустых и наполненных жидкостью оболочек. Для более наглядной демонстрации этих различий на рис. 5 приведены зависимости минимальных частот колебаний ю (Гц) от температуры T (К), полученные для разных конфигураций пустых и содержащих жидкость консольных оболочек. Из представленных данных следует, что в случае пустых оболочек нагрев внешней поверхности приводит к снижению критических температур потери устойчивости. Однако для оболочек, содержащих жидкость, имеет место, наоборот, стабилизирующее воздействие. В качестве возможного объяснения этого явления могут быть приведены следующие рассуждения. Выше было отмечено, что изменение поверхности нагрева оказывает влияние на величину нормальных перемещений свободного края оболочки. С другой стороны, значение гидродинамического давления, действующего по нормали к упругой поверхности, имеет прямо пропорциональную зависимость от величины нормальной составляющей вектора перемещений оболочки. Следовательно, раскрытие свободного края оболочки, отрицательно влияя на ее температурную устойчивость, тем не менее способствует уменьшению гидродинамического давления, оказывая стабилизирующее воздействие. Таблица 5 Критические значения температуры T (K) в зависимости от объемной доли N для оболочек с различными граничными условиями, содержащих жидкость 110 - 110- I 300 700 1100 1500 T, K 300 700 1100 1500 T, K а б Рис. 5. Зависимости минимальных частот колебаний го от температуры T для консольной ФГ-оболочки при разных конфигурациях: N = 1; арабские цифры - пустая оболочка; римские цифры - оболочка с жидкостью; сплошные линии - нагрев снизу; пунктирные линии - нагрев сверху В табл. 5 также отражены критические температуры, полученные при других геометрических размерах (h = 4х10-4 м, R/h = 500). В этом случае качественных изменений не наблюдается. Таким образом, для некоторых конфигураций нетипичная зависимость от температуры сохраняется и для более тонких оболочек. Работа выполнена при финансовой поддержке РФФИ (грант № 13-01-96049).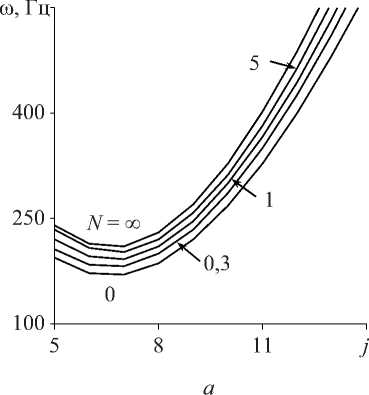
ГУ
R / h
N = 0
N = 0,3
N = 1
N = 5
N = 10
N = 30
N = да
Конфигурация I
CC
200
702,01
786,31
899,97
997,97
1000,4
994,35
987,88
500
495,53
532,22
580,15
609,19
604,72
598,24
594,11
CF
200
1031,4
1238,9
1402,6
1414,1
1398,4
1392,9
1397,5
500
671,83
814,73
1013,9
1050,5
1034,7
1032,6
1040,8
Конфигурация II
CC
200
727,91
762,54
803,02
919,38
965,93
1008,5
1033,2
500
501,15
514,62
525,58
562,04
581,04
602,35
617,29
CF
200
1637,9
1648,6
1655,3
1735,8
1765,2
1781,1
1784,8
500
1055,8
1072,0
1090,9
1221,2
1296,7
1365,1
1400,2
Конфигурация III
CC
200
987,43
814,19
720,15
689,73
693,98
699,32
701,91
500
593,85
527,12
494,77
488,42
491,48
494,31
495,48
CF
200
1397,9
1193,5
1044,3
1022,7
1034,9
1037,8
1031,8
500
1041,5
774,36
675,65
668,65
674,66
675,19
672,01
Конфигурация IV
CC
200
1034,1
972,26
890,21
790,47
764,74
742,03
728,40
500
617,89
596,22
564,94
528,36
517,81
507,72
501,38
CF
200
1784,8
1790,5
1789,9
1739,6
1707,7
1669,9
1639,1
500
1401,3
1401,0
1388,6
1277,9
1203,8
1117,6
1057,9
го, Гц го, Гц
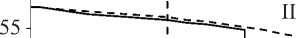
Список литературы Собственные колебания нагретых функционально-градиентных цилиндрических оболочек, содержащих жидкость
- Birman V., Byrd L.W. Modeling and analysis of functionally graded materials and structures//Appl. Mech. Rev. -2007. -Vol. 60. -No. 5. -P. 195-216.
- Haddadpour H., Mahmoudkhani S., Navazi H.M. Supersonic flutter prediction of functionally graded cylindrical shells//Compos. Struct. -2008. -Vol. 83. -No. 4. -P. 391-398.
- Mahmoudkhani S., Haddadpour H., Navazi H.M. Supersonic flutter prediction of functionally graded conical shells//Compos. Struct. -2010. -Vol. 92. -No. 2. -P. 377-386.
- Sabri F., Lakis A.A. Efficient hybrid finite element method for flutter prediction of functionally graded cylindrical shells//J. Vib. Acoust. -2014. -Vol. 136. -No. 1. -011002.
- Бочкарев С.А., Лекомцев С.В Исследование панельного флаттера круговых цилиндрических оболочек, выполненных из функционально-градиентного материала//Вестник ПНИПУ. Механика. -2014. -№ 1. -С. 57-75.
- Бочкарев С.А., Лекомцев С.В. Анализ панельного флаттера нагруженных круговых цилиндрических оболочек, выполненных из функционально-градиентного материала//Неравновесные процессы в соплах и струях: материалы X Междунар. конф. -М: Изд-во МАИ, 2014. -C. 335-337.
- Chen W.Q., Bian Z.G., Ding H.J. Three-dimensional vibration analysis of fluid-filled orthotropic FGM cylindrical shells//Int. J. Mech. Sci. -2004. -Vol. 46. -No. 1. -P. 159-171.
- Vibration characteristics of FGM circular cylindrical shells filled with fluid using wave propagation approach/Z. Iqbal //Appl. Math. Mech. -2009. -Vol. 30. -No. 11. -P. 1393-1404.
- Vibrational study of fluid-filled functionally graded cylindrical shells resting on elastic foundations/A.G. Shah //ISRN Mechanical Engineering. -2011. -Vol. 2011. -892460.
- Бочкарев С.А., Лекомцев С.В. Собственные колебания цилиндрических оболочек, содержащих неподвижную жидкость и выполненных из функционально-градиентных материалов//Современные проблемы математики, механики, информатики: материалы междунар. науч. конф. -Тула: Изд-во Тул. гос. ун-та, 2013. -С. 182-189.
- Sheng G.G., Wang X. Thermomechanical vibration analysis of a functionally graded shell with flowing fluid//Eur. J. Mech. A-Solid. -2008. -Vol. 27. -No. 6. -P. 1075-1087.
- Sheng G.G., Wang X. Dynamic characteristics of fluid-conveying functionally graded cylindrical shells under mechanical and thermal loads//Compos. Struct. -2010. -Vol. 93. -No. 1. -P. 162-170.
- Бочкарев С.А., Лекомцев С.В. Гидроупругая устойчивость функционально-градиентных цилиндрических оболочек, содержащих жидкость//Современные проблемы математики, механики, информатики: материалы междунар. науч. конф. -Тула: Изд-во Тул. гос. ун-та, 2014. -С. 133-140.
- Kadoli R., Ganesan N. Buckling and free vibration analysis of functionally graded cylindrical shells subjected to a temperature-specified boundary condition//J. Sound Vib. -2006. -Vol. 289. -No. 3. -P. 450-480.
- Bhangale R.K., Ganesan N., Padmanabhan C. Linear thermoelastic buckling and free vibration behavior of functionally graded truncated conical shells//J. Sound Vib. -2006. -Vol. 292. -No. 1-2. -P. 341-371.
- Malekzadeh P., Fiouz A.R., Sobhrouyan M. Three-dimensional free vibration of functionally graded truncated conical shells subjected to thermal environment//Int. J. Pres. Ves. Pip. -2012. -Vol. 89. -P. 210-221.
- Akbari M., Kiani Y., Eslami M.R. Thermal buckling of temperature-dependent FGM conical shells with arbitrary edge supports//Acta Mech. -2015. -Vol. 226. -No. 3. -P. 897-915.
- Бочкарев С.А., Матвеенко В.П. Численное исследование влияния граничных условий на динамику поведения цилиндрической оболочки с протекающей жидкостью//Изв. РАН. МТТ. -2008. -№ 3. -С. 189-199.
- Бочкарев С.А. Собственные колебания вращающейся круговой цилиндрической оболочки с жидкостью//Вычислительная механика сплошных сред. -2010. -№ 2. -С. 24-33.
- Вольмир А. С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. -М.: Наука, 1979. -320 c.
- Алфутов Н.А., Зиновьев П.А., Попов В.Г. Расчет многослойных пластин и оболочек из композиционных материалов. -М.: Машиностроение, 1984. -264 с.
- Reddy J.N., Chin C.D. Thermomechanical analysis of functionally graded cylinders and plates//J. Therm. Stresses. -1998. -Vol. 21. -No. 6. -P. 593-626.
- Бочкарев С.А., Матвеенко В.П. Численное моделирование устойчивости нагруженных оболочек вращения при внутреннем течении жидкости//ПМТФ. -2008. -№ 2. -С. 185-195.
- Зенкевич О. Метод конечных элементов в технике. -М.: Мир, 1975. -544 с.
- Матвеенко В.П. Об одном алгоритме решения задачи о собственных колебаниях упругих тел методом конечных элементов//Краевые задачи теории упругости и вязкоупругости. -Свердловск, 1980. -С. 20-24.
- Praveen G., Chin C., Reddy J. Thermoelastic analysis of functionally graded ceramic-metal cylinder//J. Eng. Mech. -1999. -Vol. 125. -No. 11. -P. 1259-1267.


