Собственные колебания намагниченного цилиндрического резонатора в прямоугольном волноводе

В последнее время при проектировании невзаимных ферритовых устройств КВЧ диапазона используют новые достижения в области электродинамики, конструирования, технологии и материаловедения. Особый интерес представляет изучение собственных колебаний намагниченных цилиндрических ферритовых резонаторов, на основе которых построено большинство известных устройств СВЧ и КВЧ. Однако при их проектировании, как правило [1,2], используется знание спектра ненамагниченного ферритового цилиндрического резонатора, что, естественно, затрудняет оптимизацию электродинамических параметров циркуляторов, вентилей, переключателей и т.д. Отсюда возникает необходимость исследования спектра собственных колебаний намагниченного ферритового цилиндрического резонатора и анализа соответствующего распределения полей (внутренняя задача электродинамики), исследования поля дифракции на ферритовом цилиндрическом резонаторе на частоте собственных колебаний (внешняя задача электродинамики). В предлагаемой статье исследуется спектр собственных колебаний намагниченного ферритового цилиндра.

Рассмотрим намагниченный вдоль оси z ферритовый цилиндрический резонатор (рис. 1 а) с граничными условиями Ex=Ey=0 при z=0,L и резонатор (рис. 1 б) с граничными условиями Hx=Hy=0 при z=0,L. Так как цилиндр намагничен вдоль оси z, то собственные колебания в структуре распадаются на независимые колебания двух групп, причем для одной группы в плоскости z=L/2 справедливо граничное условие Ex=Ey=0 (электрическая стенка), а для другой Hx=Hy=0 (магнитная стенка). Очевидно, что в устройствах с ферритовым элементом, высота которого равна размеру волновода, возбуждаются колебания обоих типов.

Если высота ферритового элемента меньше высоты волновода(рис.1 в), то при достаточно больших значениях диэлектрической проницаемости феррита £ф (Еф>10) и размерах зазора s (между верхним основанием цилиндра и стенкой волновода), когда влиянием верхнего основания ферритового цилиндра можно пренебречь, граничное условие на этой поверхности имеет вид: Нт = 0 [2]. Поэтому собственные колебания резонатора с неполным заполнением (рис.1 в) и резонатора, геометрия которого показана на рис.1 а, могут быть использованы при проектировании Н- и Е-плоскостных невзаимных устройств как с ферритами, высота которых меньше волновода, так и с ферритами, высота которых равна размеру узкой стенки прямоугольного волновода.

Рассмотрим резонаторы, геометрия которых приведена на рис.1 а и рис.1 б, в предположении отсутствия вариации поля вдоль оси z. В этих случаях уравнения Максвелла распадаются на две системы: одна(рис.1 а)-для составляющих Ez, Нф Hr (TM- колебания), а другая (рис.1 б )-для составляющих Hz, Eф, Er (TE-колебания). Им соответствуют волновые уравнения в цилиндрической системе координат [3]:

различные

∂ ²E_z ∂ r²

+ ₂ r

_{1 ∂} 2_E

z

∂ϕ ²

1 ∂ E + ^z

r ∂ r

+ ^к Цу. ^Е ф E z   ⁰ ,

для TM - колебаний и

∂ ²H_z ∂ r²

∂ ²H_z

r² ∂ϕ ²

1 ∂H + r ∂r

— + к^{2 Ц} Е ф ^H _z = 0 ,

для TE- колебаний, где цу = ц - Ц2 / ц, ц = 1; ц, ца - соответственно диагональная и недиагональная компоненты тензора магнитной проницаемости феррита, k = to / c - волновое число.

С учетом периодичности поля по азимутальной координате ф можно принять, что поля E, H ~e^{l v}

, где v =0, ± 1, ± 2,...,что позволяет рассматривать азимутально бегущие волны по часовой стрелке ( ν >0) и против часовой стрелки ( v <0).

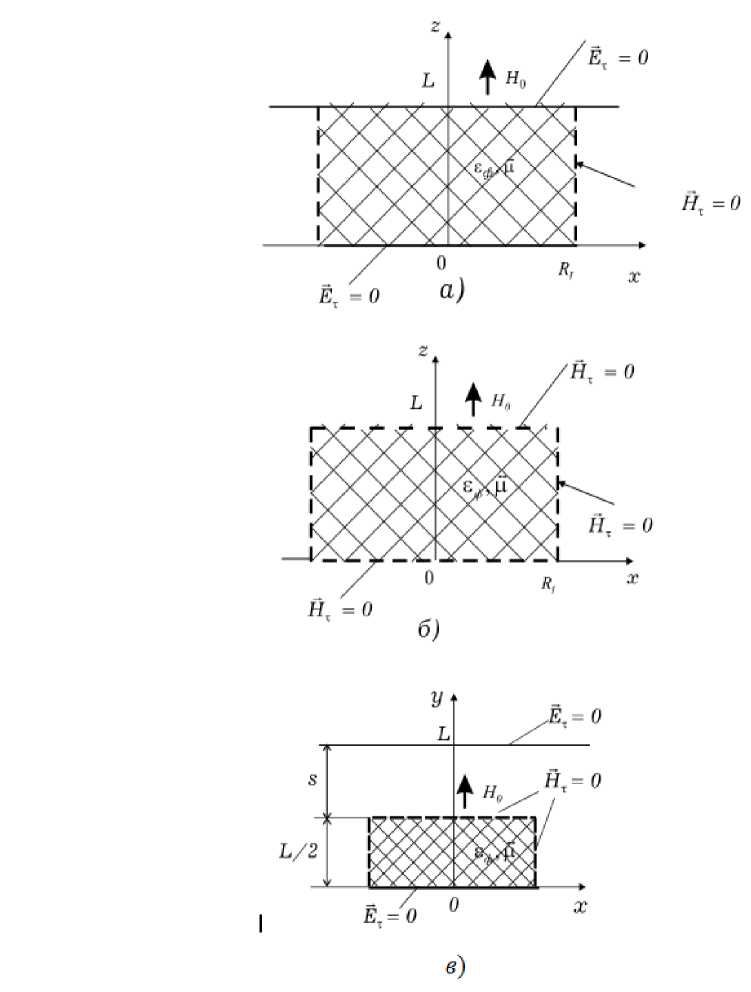
Рис.1. Геометрия цилиндрического ферритового резонатора

Чтобы получить уравнения для определения собственных частот резонаторов (рис.1 а, рис.1 в), обратимся к модели резонатора с магнитными стенками (Hz=Hv=0 при r=R1) на боковой поверхности ферритового цилиндра [2]. В этом случае уравнения для определения собственных частот имеют вид:

J'v(kR 1 Т^^^Т) +    Jv(kR 1J^) = 0,       (3)

для TM - колебаний и

Jv (kR1 J^ ) = 0, для TE- колебаний, где Jv(kR 1) =

d J v (kr) d r

,J _v (x) - функция Бесселя первого рода r = R 1

порядка v .

Рассмотрим более подробно собственные колебания с v =0, ± 1. Для TM -колебаний имеем

J0 (kRi V£™Hi)

= 0, при v = 0,

Ц Ц 11J

к Ц 7

(kR1 yj £фЦт ) ± kRi ^ £ф^т Jo (kRi л] ^ф^Т )

= 0  ,   (6)

при v = ± 1, причём верхние знаки в (6) соответствуют v =1, а нижние- v =-1.

Аналогично, для TЕ - колебаний

Jo (kRi dkkh, ) = 0 -

Ji (kRi 44фЦ ) = 0,

при v = 0, при v = 1.

Из соотношений (5-8) можно сделать следующие выводы:

• 1.    Характеристики TЕ - колебаний намагниченного ферритового резонатора (рис.3.1 б) при ц =1 совпадают с характеристиками собственных колебаний диэлектрического резонатора. В частности

• 2.    Так как невзаимность устройств СВЧ и КВЧ диапазонов с цилиндрическим ферритовым резонатором связана с невзаимными свойствами резонатора вдоль координаты ф , то ТЕ -колебания не могут играть определяющую роль при объяснении принципа работы ферритовых устройств СВЧ и КВЧ диапазонов.

• 3.    Можно предположить, что принцип работы ферритовых устройств КВЧ с цилиндрическим ферритовым резонатором основан на возбуждении ТМ - колебаний с v = ± 1, свойства которых зависят от внешнего подмагничивающего поля. Для этих колебаний собственные частоты, при определенных условиях, могут значительно отличаться.

собственные частоты этих резонаторов для   v=±1   являются вырожденными.

Остановимся более подробно на анализе собственных колебаний ферритового цилиндрического резонатора ( r = R 1 ) с граничными условиями ρ

Н т = 0 на боковой поверхности цилиндра и сравним со спектром собственных колебаний диэлектрического резонатора. Некоторые численные результаты анализа, проведенного на основе соотношений (3-6), показаны на рис.2-5, на которых приведены зависимости собственных частот от радиуса R₁ ферритового резонатора для диэлектрического (ненамагниченного ферритового) и намагниченного ферритового резонаторов. Будем классифицировать собственные колебания структуры (рис.1) тремя целыми числами ( i, v m ), где i ( i =1,2,3,...)- характеризует вариацию поля вдоль координаты r ; v ( v =0, ± 1, ± 2,...)- характеризует вариацию поля вдоль ( v >0) или против ( v <0) ф ; m - число вариаций поля вдоль оси z .

На рис.2 изображены дисперсионные характеристики для ТМ -колебаний намагниченного (сплошные линии) и ненамагниченного (штриховые линии) ферритового цилиндра марки IC44 с диэлектрической проницаемостью ε ф =11.1, намагниченностью насыщения M 0 =382 кА/м.

Расчёты проведены при внешнем подмагничивающем поле H₀ =500Э ( ^ = 1 ). Из рис.3 следует, что на спектр собственных колебаний существенное влияние оказывает значение диэлектрической проницаемости. С ростом значений £ ф спектр собственных ТМ -колебаний смещается в сторону более низких частот. Влияние постоянного подмагничивающего поля Н_о на смещение собственных частот ТМ - колебаний ферритового резонатора марки 1СЧ4 показано на рис.4. Анализ полученных численных результатов показывает, что на спектр собственных колебаний в большей мере влияет намагниченность насыщения феррита М₀ .

Собственные частоты колебаний ТМ-полей (рис.2-4), кроме колебаний типа (i,0,m), расщепляются при v=±1. Заметим, что при этом знак параметра v зависит от направления подмагничивающего поля Но: при смене направления внешнего подмагничивающего поля Но на противоположное меняется знак параметра v. Анализ зависимостей на рис.2-4 показывает, что собственные частоты колебаний ТМ с v> 0 лежат по частоте значительно ниже, чем частоты c v<0. Поэтому можно всегда указать некоторый интервал частот А/ в котором будет возбуждаться только одно колебание с заданным вращением (v>0 или v<0).

При проектировании невзаимных устройств на основе цилиндрического ферритового резонатора часто важно знать распределения полей собственных колебаний на боковой поверхности ферритового резонатора. Распределения полей собственных ТМ - колебаний на боковой поверхности резонатора (r = R 1 ) с магнитными стенками (рис.1 в )

определяются соотношениями:

EZv)(Ri ,р) = vAJi

(kv R1 ^ £фМ1) exp( i vP)

Hp)(R1 ,ф ) =

Av (f M

wvu.M0 [vMR

v

Ri)

J1

( kv Ri ^ £фЦ^ )

Makv^j ефМ1.

M

J 0 ( ^k v ^R1 л) ^£ ф ^ 1) * ^ex P ^{( i v}^ )

для V = ± 1,

где каждому значению v=±1 соответствует свое собственное число kv = tov / c, которое определяется из уравнения (6), А - некоторая постоянная, определяемая из условия нормировки. Можно отметить, что важной особенностью азимутальных распределений полей намагниченного ферритового резонатора является их комплексный характер, при котором составляющие поля ТМ- колебаний имеет как действительную, так и мнимую составляющие.

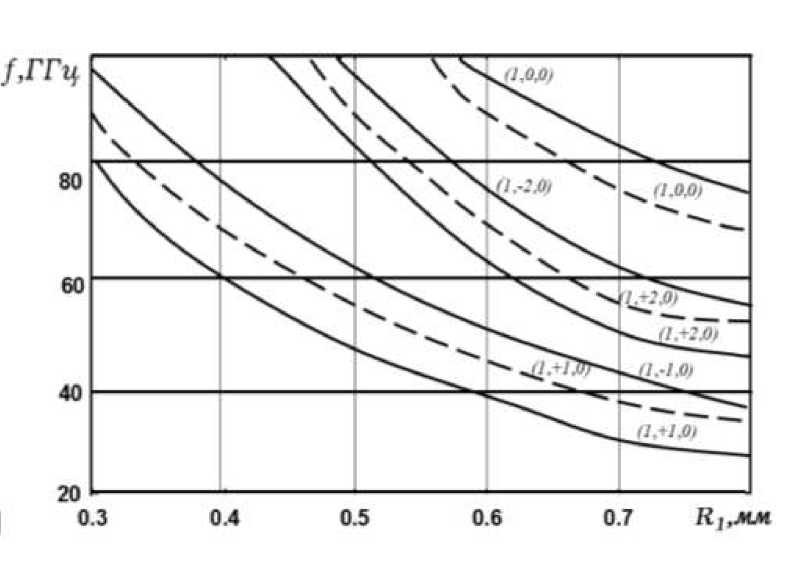
Рис.2. Дисперсионные характеристики для ТМ - колебаний намагниченного (сплошные линии) и ненамагниченного (штриховые линии) ферритового цилиндрического резонатора

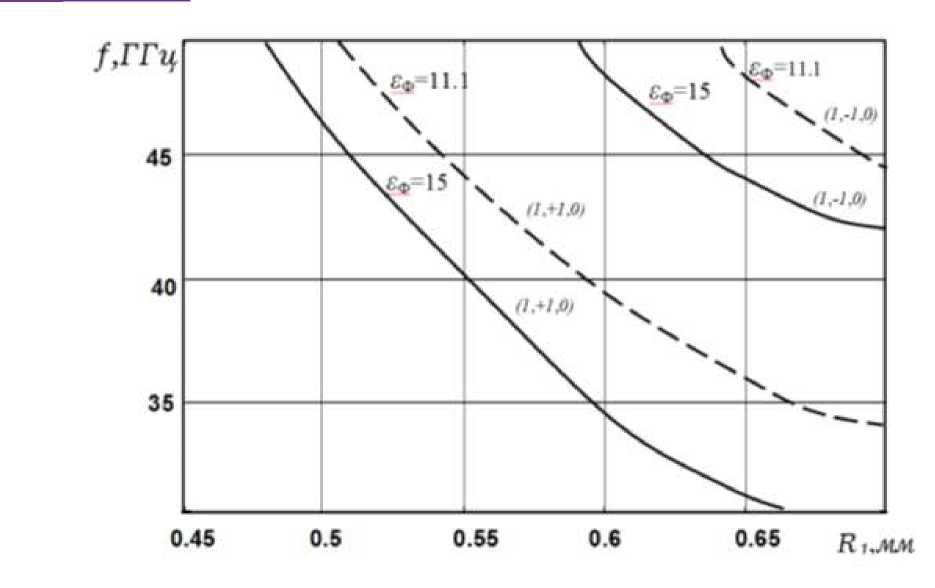
Рис.3. Дисперсионные характеристики ТМ - колебаний намагниченных цилиндрических ферритовых резонаторов марки 1CЧ4 с различными диэлектрическими проницаемостями

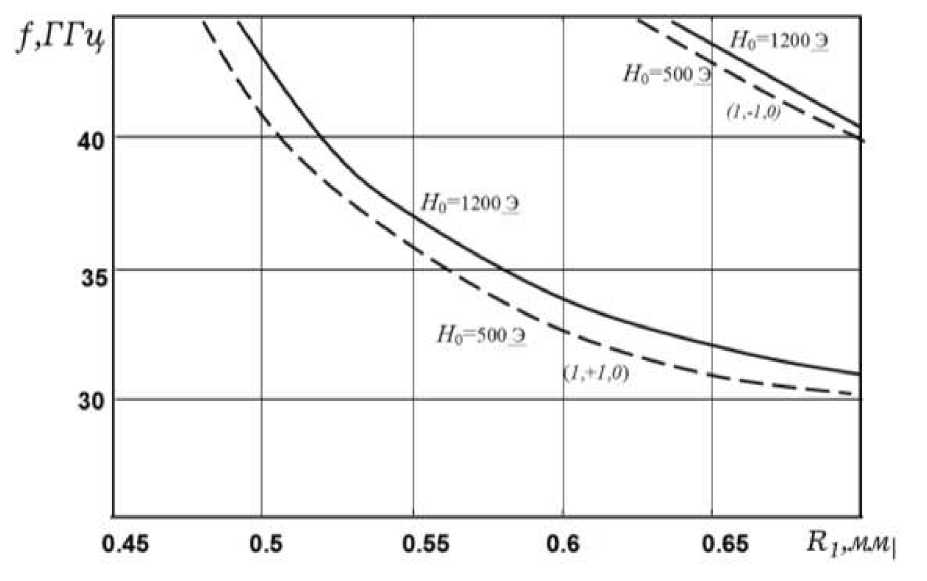
Рис.4. Дисперсионные характеристики ТМ-колебаний цилиндрического ферритового резонатора при разных подмагничивающих полях