Собственные колебания наполненного жидкостью упругого цилиндрического капилляра конечной длины. I. Теория

В работе [1] была рассмотрена задача о собственных акустических колебаниях неоднородного цилиндра, состоящего из стеклянной трубки, заполненной жидкостью. При этом учитывались только объемные (продольные) колебания в стенках трубки. Для выяснения правомерности такого допущения в настоящей работе сделана попытка учета упругих свойств стенок трубки, т. е. рассмотрены еще и сдвиговые волны, а следовательно, получена возможность выявить степень расхождения со случаем пренебрежения упругими свойствами стенок трубки, рассмотренным в [1].

Вопросу рассмотрения упругих колебаний в полых цилиндрах посвящено достаточно много работ. Так, в работе [2] рассматриваются аксиально-симметричные, а в работе [3] — произвольные упругие гармонические волны в бесконечном полом цилиндре в вакууме; результаты сравниваются с аналогичными, полученными из теории оболочек. В работах [4–6] изучаются резонансные явления в бесконечном полом цилиндре в идеальной жидкости под воздействием различных нагрузок. В работе [7] рассматриваются упругие колебания сплошного цилиндра конечной длины в вакууме.

В настоящей работе изучаются резонансные явления в системе, состоящей из полого упругого цилиндра конечной длины, заполненного изнутри жидкостью, а снаружи контактирующего с вакуумом.

ПОСТАНОВКА ПРОБЛЕМЫ

Пусть дан круговой кольцевой цилиндр, высо- той l , внутренним радиусом a1 и внешним радиусом a , состоящий из некоторого материала плотностью ρ и со скоростями продольных cl и поперечных (сдвиговых) ct волн. Внутри кольцевого цилиндра находится основная жидкость, с постоянной плотностью ρw и скоростью звука cw . На границах цилиндра справедливы однородные условия Дирихле. Необходимо оценить собственные колебания описанного объема.

РЕШЕНИЕ ЗАДАЧИ

Остановимся на уравнениях колебания в упругой полой трубке конечной длины. Выпишем уравнения Ламе для линейно-упругой однородной изотропной среды в отсутствие внешних источников [7]

d2u р---= (Л + ц) grad div u + ц Au .     (1)

d t ²

Здесь u — вектор смещения; λ и µ — упругие постоянные Ламе. Если представить u = grad Ф+rot T = ul + ut,           (2)

где ul = grad Ф,    u t = rot T, то уравнение (1) распадается на два уравнения для скалярного Ф и векторного T потенциалов:

д 2 Ф

—- = c ² АФ , д t ^{2      1}

— = c ² A Y , д t ²       t

^cl ²

X + 2 ц

^{, ρ}

2 µ c t

ρ

.

Перепишем систему (3) применительно к цилиндрической системе координат, т. е. преобразуем ( x , y , z ) ^ ( r , ф,z ) [8, с. 358, 361]:

^O rr = ( ^{X + 2} Ц ) ^S rr ^{+ X} ( Е фф + S zz ) ,

° фф ^_ ( ^{X +} 2 Ц ) ^S фф ^{+ X} ( ^S rr ⁺ S zz ) ,

O zz = ( X ⁺ 2 ц ) £_B ⁺ X ( S rr ^{+ S} фф ) ,

^гф = ² Ц^S r ф , ^O rz = ² ^rz ,    ^z = ² Ц^S Ф Z ;

и выражения напряжений через потенциалы [9, с. 36]:

д 2 Ф —— = д t ф-	С 2 АФ ,
2	, f      И дYф    11
r	= ct2 AY r --2--- ф + Y r I ,
д t	r 2 V   д ф      Л
	(4)
д 2 Y ф	, f       1 1 SY      11
	= c 2 AYf+ — 2-- r- — Y   ,
д t "ф	t V ф r 2 V д ф       ф II ,
д 2 Y
z	= c t 2 AY z ;
д t "ф

1 r

д ( r Y r ) + дY ф д r      д ф

5YZ n

+ —- = 0; д z

,    1 д f  дЛ    1   д ²      д ²

А =--I r — 1 +--+--- .

r д r V д r J   r ² д ф ²    д z ²

Связь поля смещений с потенциалами следующая:

дФ 1 дY z дY ф

⁺ —;^, д r r д ф    д z

1 дФ дY _r дY z

1 , r д ф д z     д r

. д ² Ф д[ 1 дY o_rr = Х АФ + 2 ц —- +---^:

^ д r ² д r V r д ф

°_w = ^{Х АФ+} 2 ц - ^х r

f 1 д ² Ф дФ х--+--+

_V r д ф ² д r

п = ХАФ ■ 2 ц zz

σ r ϕ

z

—

дY ф д z

,

д 2 Y r	дY ф		1 дYz +--- r д ф	д 2 Y z 1
д ф д z		д z		д r д ф J
д 2 Ф + д z2	1	Гд	f?Y ф 1	д 2 Y r !'
	r	д r	V д z J	д ^ 5 z

,

„ д f 1 дФ

= ц < 2— I-- д r V r д ф

1 д ² Y _z

+--- r2 дф2

<7 = Д/ ϕ z   µ

—

д 1 f SY,

+ r— — д r r

1 д ² Y ф

r д ф д z ;

2 д ² Ф    1

--+ —

д( дY_<

r д ф д z r ² д r

д ² Y

+----- r

—

д ² Y _z

д z ²     д r д z

;

r

—

дY _z

д z    д r

+

(9а)

r

V

’ ф 1   д ² Y r

—

д ф J   д ф²

+

_о д ² Ф д f 1 дY_r

Orz = Ц 2---1--- дrдz дr V r дф

д fY.

+ — д r

^ф 1 +

V ^r

дФ 1 Г^д ( ^{r Y} ф ) дY r 1

д z r    д r      д ф

Приведем также выражения для тензоров напряжения и деформации [8, с. 360]:

εrr	_ д u д	r ,    S. _ 1	д и ф + u r. д ф r
		,       ϕϕ r
ε	_ 1	fд и ф , 1 д ur 1	и ф 1
r ϕ εrz	2 _ 1	V д г   г дф " д ur   д u z 1 rz ч д z    д г J ,	r J
ε ϕ z	_ 1	^д Ц ф + 1 д U z ' V д z г дф у	) ;

εzz

д uz дz ’

_| ^{д 2 Y} ф д r ²

—

д2Y ф  1 д2Y ф +z дz2   r дzдф

.

Далее поставим краевые условия на внутренней и внешней поверхностях цилиндрической трубки, а также на ее торцах. Внешняя поверхность при r = a граничит с вакуумом (свободная граница), внутренняя поверхность при r = a 1 граничит с жидкостью. На свободной границе равны нулю компоненты тензора упругого напряжения

(7 =<7 =<7 =0. (10) rr r ϕ rz .

Внутренняя поверхность трубки граничит с идеальной жидкостью. В этом случае справедливы следующие граничные условия [10, с. 442].

– Нормальное напряжение на границе равно давлению в жидкости, взятому с обратным знаком;

касательные напряжения равны нулю; нормальные скорости твердого тела и жидкости на границе равны между собой:

^Ar = a 1       P w\r = a1 ’

UtA r r = a1

v . wr l r = a

^.„ I   = CT J   = 0, гф lr = a1        rz'r=a

– На торцах трубки равны нулю компоненты тензора упругого напряжения:

CT₇₇    = ^     = CT_    = CT„   , =

== 1 = = 0         = ^ф \ = = 0         ^r=\= = 0         ==\= = 1

= ^ =ф|= = 1 = ^ r=|= = l = 0.

В жидкости поле для потенциала колебательной скорости описывается волновым уравнением

^-^ = c ² АФ .

d t ²      w w

Здесь Ф w — потенциал колебательной скорости v _w в жидкости. Колебательная скорость и давление P_w в жидкости выражаются следующим образом:

v w = g ^{rad ф} w ,    P w = - P w — .      (14)

d t

Краевые условия на границе с полым цилиндром приведены в (11); на торцах цилиндра при = = 0, 1 равно нулю давление в жидкости

Р I = Р I =0

^w l = = 0 ^w l = = 1

Полагаем, что рассматривается стационарный гармонический процесс. Поскольку ниже амплитуда колебаний рассматривается в вещественной форме, временной множитель принимаем в форме cos ωt . Для потенциалов смещения в упругой трубке (оставлены те же обозначения для простоты изложения) получаем из (4) следующую систему:

АФ + ^ 2 Ф = 0.
2 cl 2 AV + — V zz ct 2	= 0;	(16)
L 1 — 2) A1	2 dV V r---ф = 0,
22 V      r     ct 7 Г      1       2 7 A 1     — 2 A1	r 2 д ф 2 dV V + — ^-^ = 0.	(17)
r 2   c2 V      r      ct 7	ϕ 2

Для давления в жидкости имеем:

A P + — P„ = 0.          (18)

ww c ² w

Здесь лапласиан А имеет вид (6). Решение системы (17), (18) ищем в виде произведения функций от одной переменной, что является стандартным для отыскания собственных колебаний.

В работе [3] для полого, а следом и в [11] для сплошного бесконечного цилиндра предложено искать решение свободных колебаний в следующем виде:

Ф = f ( r ) cos тф e^l^^z ,

V _r = g_r ( r ) sin тф e^ ^z ,

V ф = д ф ( r ) cos тф с- ,

V = = д = ( r ) sin тф e^l ^^z ,      т = 0,1,2,...

В работе [1] применительно к случаю жидких слоев давление искалось в виде

P w = f w ( r ) е '^{т ф} sin ^ k = , т = 0, ± 1, ± 2,...

Учитывая, что на интервале ф е [0,2 ^ ] полной является либо система функций { е '^{т ф} } , т = = 0, ± 1, ± 2,..., либо система { cos тф , sin тф } , т = = 0,1,2,..., решение задачи будем искать двояко.

В первом случае ставим задачу во внутренней жидкости

Pw = fw(r)- cosтф-sin-.=, r e[0,ad(19)

и в полом упругом конечном цилиндре:

Ф ^c = f ^c ( r ) - cos тф - L (§_k= ),

V r^c = g r^c ( r ) - sin тф - L / ( ^ k = ),

Vф = дфС (r) - cos тф - 4 (fk=)»

^V =^c = g =^{c ( r} ) ^- sin ^т ф ^- L =^{c (} f k = ), r e [ a 1 ,a ].

Во втором случае соответственно

Pw = fw (r) - sin тф-sin ^k=, r e[0, a1],(19а)

Ф ^s = f^s ( r ) - sin тф - L ^s (§_k= ),

V r^s = g r^s ( r ) - cos тф - L r^s (^ k = ),

Vф = дф"(r)- sin тф - Lфs (^k=)»

V=s = g=s (r)- cos тф - L=s (^k=), r e[a1,a].

Здесь

L ( ξ k z )

kπ cos    z, l, kπ sin    z, l,

В

ределенная пока в каждом

z e [0, l ] — неоп-конкретном случае

функция, равная либо cos ξ_k z , либо sin ξ_kz , выбор

которой будет пояснен ниже; ^k = kn, k = 1,2,... — дискретные значения продольной составляющей волнового вектора, выбранные таким образом, чтобы удовлетворялись граничные условия (15) на торцах трубки в столбе жидкости. Верхний индекс c и s в выражениях (19)–(20а) зависит от того, какая функция — cos или sin — взята в азимутальном сомножителе выражения для давления в жидком цилиндре. Теперь, следуя технике [3], получаем уравнения для радиальных составляющих из (20):

^B m, a. r [ f " ( Г ) ]- °,

^B m , ,k , [ g' ( Г ) ]- °,

^В m + 1, ek r [ g r' ⁽ r ) - g . " ⁽ r ) ] = °,

^B m - 1, „ [ g r" ^{( r} ) ⁺ g . " ^{( r} ) ]= °-

где оператор В определяется следующим образом:

д ²    1 д    ( m ²

1I

5 x ²    x д x I x x

Pk2 = to — ^k2.

^ct ²

Действуя аналогично, получаем уравнения для радиальных составляющих из (20а):

^В m_w [ f s ( r ) ]= °,

^В m ek r [ gp ( r ) ]= °,

^В m - 1, _{P t}r [ gP ⁽ r ) - g . ⁽ r ) ] = °,

^В m + 1,_Ptr [ g rs ⁽ r ) ⁺ g . s ⁽ r ) ] = °.

Функции f_w ( r ) из (19), (19а), а также общее решение (21), (22) выражается в терминах цилиндрических функций Бесселя J и Y или модифицированных функ ц ий Бесселя I и K от аргументов a_kr = | a_kr | и P_kr = | e_kr |, как показано в таблице (в первых двух строках таблицы принято обозначение 6 k = ^ k |, ^ kx = ^ _? - ^ k² ).

^cw ²

Введем обозначения: 2 g 1 = g_r - g . , 2 g 2 = g_r + g . , g 3 = g z . Тогда общими решениями уравнений (21), (22) будут соответственно

Функции, используемые при решении уравнений (19), (19а), (21), (22)

Интервал по частоте Используемые функции to < ^k"w I(σkr) to > ^k"w J(σkr) to < ^k"t I(αkr), K(αkr), I(βkr), K(βkr) ^k"t < to < ^k"l I(αkr), K(αkr), J(βkr) , Y(βkr) to > ^k"l J(αkr) , Y(αkr) ; J(βkr) , Y(βkr) fc (r) = AZm (akr) + BWm (akr), g3c (r) = A3Zm (вкГ) + B3Wm (вкГ),

• ² g 1 c ⁽ r ) = ( g rc ⁽ r ) - g p ⁽ r ) ) =

= 2 A Z m + 1 ( P k r ) + 2 BW + 1 ( P k r ),

• ² g 2 ^{c ( r} ) = ( g rc ^{( r} ) + g p ^{( r} ) ) =

= 2 A 2 Z m - 1 ( e k r ) + 2 B 2 W m - 1 ( e_kr ) и

• ^{fs ( r} ) = AZ m (tt^ ) + BW m ^{( a} k r ),

g 3 s ( r ) = A 3 Z m ( Hr ) + B 3 W m ( e k r ),

• 2 g 1 s ( r ) = ( gp ( r ) - g p ( r ) ) =

(23а)

= 2 A i Z m - i ( P k r ) + 2 BW - i ( P k r ),

• ² g 2 s ^{( r} ) = ( gp ^{( r} ) ⁺ g p ^{( r} ) ) =

= 2 A Zm+1(Pkr) + 2 B 2 Wm+1( ekr), где Z символизирует функции Бесселя J и I , а W — соответственно Y и K .

Как известно [12], согласно принципу калибровочной (градиентной) инвариантности, существует возможность определять векторный потенциал смещения с точностью до градиента произвольной скалярной функции. В работе [3] для удобства расчетов это реализуется приравниванием нулю функции g ₂ ^c ( r ) из (23). Окончательно это приводит к равенству

• g r = - g p = g 1 .

Отсюда имеем grC = - gp' = g 1C = A1 Zm+1 (Pkr) + BiWm+1 ( Pkr), gP = — gp = g 1 s = A Zm-1 (ekr) + BWm-1 (ekr).

Окончательный вид решений определяется видом решений в жидком слое (19), (19а), где продольная составляющая обязательно должна быть равна sin ξ_kz для удовлетворения краевых условий на торцах жидкого слоя. Кроме того, исходя из первого и последнего краевых условий (11) на границе слоев, а также исходя из вида решений в жидкости для поля давления (19) и (19а), возможность сопрягать парциальные решения для всех m и k появляется лишь при совпадении тригонометрических сомножителей в обеих средах. Как легко получить, рассматривая первое и последнее краевые условия (11), выражения для напряжений (9а) и соответствующих (20), (20а) смещений, таковыми являются решения для потенциалов в упругом слое

Ф ^c = f ^c ( r ) cos mp sin p_kz ,

V p = g_r ^c ( r ) sin mp cos p_kz ,

V p = g p ( r ) cos mp cos pz ,            (26)

^p = gzc (r) sin mф sin ^kz, r e[a1,a] и фs = fs (r) sin m^ sin ^kz,

V _r ^s = g_r ^s ( r ) cos m^ cos ^_kz , ^ P = g P ( r ) sin m^ cos p^z , V Z = gp ( r ) cos mp sin p k Z , r e [ a 1 , a ].

(26а)

соответственно для решений в жидком слое (19) и (19а). Отсюда из (7) получаем выражения для смещений:

up =l ( f ^c ) ' + mg 3 ^c - P k g 1 ^c I cos mp sin P k Z ,

V r

( m upc =|--fc - pkg 1c -(g3c) IsinmPsinpkz,

r

(               \ , ^{m + 1} „I

U z^c =| f ^c P_k - ( g 1 ^c )-- g 1 ^c I cos mp cos p k Z

V

и up =1 (fs)'- mg 3 s - Pkg 1 s I sin mpsin PkZ,

V r)

(m1

ups =| —fs -pkg 1 s-(g3s) IcosmPsinpkz,

r

U zs =| f s P - ( g 1 s ) ' + m- ¹ g 1 s I sin mp cos p k Z .

V

Здесь штрих означает дифференцирование по r .

Из (9а) и (26), (26а) найдем выражения для напряжений на торцах трубки и на боковой поверх

НОСТИ <7 , <7 , <7 , <7 И <7 :

rr , rϕ , rz , zz        zϕ mm

^(-kf) + 2Ц f +—g3 - pkg1 ±-g3 fx r2

[cos mp I x< .      [ sinpkZ,(29)

[ sin mp

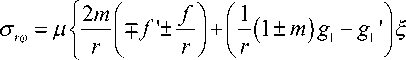
- ( в ² g 3 + 2 g ₃" ) |

sin mp I

[ sin p k Z , cos mp

If 1 ± m „ A 1 ± m

°rz = ^ 1I ”--^k I g 1--g 1 -

IV r²          J r

— Xk , ² f + 2 ц

mm f + — g3 — ^kg1 ±—g3

r 2               r

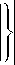
= 0,

^— g i

"± ^ g 3 + 2W' r

cos тф I f cos ^ k Z , sin тф I

m f

ц!—I + f±—I+I-(1 ±m) g 1— g 1 I ^k—L r V r J V r                J

σ

zz

—

= 0,

— Xk, ² f + 2 ц

S ² f + ^ ( 1 ± m ) g i + ^g i ' r

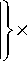
r = a

I cos тф I x! .      f sin ^ k Z ,

| sin тф

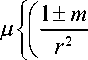
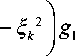
1 ± m --g 1 ^— g 1

r

±

CTZф = Ц 1 +

2 mξ k f

m (m ± 1)

—

r

V

r ²

^ξ k ²

±

± ^m ^ g 3 + 2 ^ k f r

= 0.

r = a

⁺ g 1

± ^{2 m} g 1 ' r

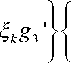
sin mϕ cos mϕ

cos ξ_k z .

Верхний знак или функция в (29–33) относится к решению (26), нижний — к решению (26а).

Первые три граничные условия (11) принимают вид:

— Xk l ² f + 2 ц

mm f + — g 3 — ^kg 1 ±— g 3

r ²               r

r = a_A

f w L= a , ,

m f

ц!—I +f ±— H _0 ±m) g 1— g 1 I -■ -I r V r J V r                J

—

r = a₃

= 0,

—

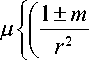
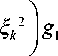
1 ± m g 1

r

' - g 1 ” ±

± ^m ^ g 3 + 2 ^ k f r

= 0.

r = a j

Четвертое условие получаем из (27), (28), а также из уравнения Эйлера для идеальной жидкости

m f ±— g3 — ^kg 1 r

a ₁

V P w ® ²

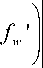
Краевые условия (10) на внешней боковой поверхности r = a имеют вид (см. (34)-(36)):

В (34)–(40) необходимо различать g ₁ для случаев (c) и (s).

Обратимся к краевым условиям на торцах (12). Как видно из (32), напряжение σ_zz на торцах трубки равно нулю вследствие наличия множителя sin ξ_kz . Исследуем возможность удовлетворения краевых условий (12) для напряжений σ_rz и σ_zϕ . Из (31) и (33) очевидно, что краевые условия (12) могут быть удовлетворены при произвольных ϕ и r , а также m и k , только когда радиальное слагаемое в фигурных скобках тождественно равно нулю на интервале r e [ a ₁, a ], что невозможно вследствие линейной независимости стоящих там комбинаций цилиндрических функций. Таким образом, напряжения σ_rz и σ_zϕ краевым условиям (12) не удовлетворяют. Однако следует ожидать [7, с. 303], что при условии большой величины отношения длины трубки к ее диаметру и выполнении остальных краевых условий напряжения σ_rz и σ_zϕ на торцах трубки будут пренебрежимо малыми.

Таким образом, для определения шести неизвестных констант A , B , A ₁, B ₁, A ₃, B ₃ из (23), (23а) и (25) при каждом m = 0,1,2,... и k = 1,2,... для случаев (c) и (s) имеется по семь уравнений (34)– (40). Остающееся лишнее уравнение (им будет уравнение (38), являющееся единственным краевым условием на поверхности r = a в предельном случае жидкой трубки) будем использовать для определения резонансных частот, аналогично тому как это делалось в работе [1].

После подстановки в систему (34)–(37), (39), (40) выражений (23), (23а) и (25) получаются две системы для определения констант A , B , A ₁ , B ₁ , A ₃ , B ₃ для случаев (c) и (s). Запишем их в матричном виде:

C =

S =

Г A )

B ^c

A 1

B 1

A 3

D c

к B 3 7

( A s )

B ^s

A 1

B 1

A ₃

R s

B з 7

- L ( a i ) = ^— Z m ⁽ ^ k a i )

1 ρ_wω ²

к

f w '( a i ) =

¹    Z_m '( σ_k a ₁)

ρ_wω ²

- ^fw ⁽ a l ) = ^— Z m (^ k a i )

1 ρ_wω ²

,

Квадратные матрицы C и S состоят соответственно из элементов c„ и s„, i, j = 1,2,..., 6. Все ij               ij элементы уравнений (41), (42) зависят от индексов m , k и частоты ω , что подразумевает необходимость находить соответствующие решения для конкретных значений этих параметров. После громоздких, но несложных вычислений получаем для элементов cij и sij :

f w '( a ) = —

ρwω

₂ Z_m '( σ_ka ₁)

.

C 11 = ~ Ak_l²Z m ( a k a 1 ) + 24Z "( a k a i ),

C 12 =— ^k i 'W m (a k a i) + AW ^a i ),

C 13 = — 2 ц^ + i '( в к ад,

C 14 = — 2 ^k W m + 1 '( в к а 1 ),

2 mµ

Ci5 =----- a1

2mµ ci6 =— a1

Z m '( P k a i )

к

W m '( e k a i )

к

—

Z m ( e k a i ) )

a ₁

—

W m ( β k a 1 )

ai 7

,

^C 21 ⁼ 2 m ^{2 Ц} ( ^Zm ^{( a} k^ai ) - a i ^Zm '( “ k a i ) ) ’

^C 22 = ^ m^{4 W}m ^{( a} k a i ) - a i ^Wm '( O t a i )) ,

^k ((1 + m)Zm+i(ekai) — aiZm+i'(Pkai)) C 23 = a1

_ ^k ((i + m) Wm+i (ekai) — ai Wm+i'(Pai)) C 24 = a1

sii = Cii, si2 = Ci2 , si3 =— 2ц:// —1'( Pkai), si4 =—2ц:kWm—1'( Pkai), s15 = - C15 , si6 = -C16 , s 21 = -C 21 , s22 = — C22 ,

^k ((1 — m)Zm—i(Pkai) — aiZm—1'(Pkai)) s 23 = a1

^ik ((1 — m) Wm—i(Pai) — aWm—i'(Pai)) s 24 = a1

C 25 =— 4 ( m ² Z m ( P k a i ) + a i ( a i Z_m "( P k a^ — Z_m '( P k a^ ) ) , s 25 = ^C 25 , a ²

c 26 = — оц т ( m ² W m ( P k a i ) + a i ( a i W m "( P k a i ) — W m '( P k a i ) ) ) ,     ^s 26 = ^C 26 ,

c 31 = ² Ц^ k^Zm '( O A),

^S 31 ^{— C} 31 ,

c 32

= 2 H^W m '(a_ka i ),

s 32    ^C 32 ,

c 33

— ц

((л , 1 + m

—

a 1²

( ² Z m + 1 ( в к а 1 )

—

s 33

— Ц

(Га ™

^{1 —} m

Ц а 12

—

( ² Z m — 1 ( в к ^) —

—

- ( 1 + m ) Z m + 1 '( в к ^) — z, a ₁

'm + 1" ( в к а 1 ) I ,

— -( 1 — m ) Z m — 1 '( в к ^) — Z m — 1 ''( в к а 1 ) I , ^а 1                                            J

c 34

= ц

((a , 1 + m

Ц t2

—

( ² W m + 1 ( в к а 1 )

—

s 34

— Ц

1 — m a ₁ ²

— ^ к ² I W m — 1 ( в к а 1 ) —

—

-(1 + m ) W m + i '( в к а 1 ) — W m Л в к ^) I , а ₁                                             J

— -( 1 — m ) W m — 1 '( в к а 1 ) — W m — 1" ( в к а 1 ) I , а ₁                                             J

c

35 = "^ Z . ( в к а 1 ), a ₁

s 35 ^{—   C} 35 ,

C 36 — Mm^LW_m ( в к а 1 ), a ₁

^C 41 = ^Zm '( «A ),

^C 42 = ^Wm '( « А),

s 36      ^C 36 ,

s 41    ^C 41 ,

C 43 =— -/. ₊ 1 ( в к ^),

s 42    ^C 42 ,

S 43 — — / . — 1 ( в к а 1 ),

C 44 =— ^ k W m + 1 ( в к а 1 ),

S 44 — — ^W m — 1 ( в к а 1 ),

mZm(βka1) c 45 — a1

mW_m ( β _ka ₁ )

C46 —------------- a1

^S 45       ^C 45 ,

^S 46      ^C 46 ^.

Коэффициенты c ₅ j и s ₅ j , j — 1,6 равны соответственно коэффициентам c _{2 j} и s _{2 j} , в которых, однако, фигурирует a в место a ₁ . То же справедливо соответственно для коэффициентов c _{6 j} , s _{6 j} и c _{3 j} , s _{3 j} .

Вернемся к алгоритму вычисления резонансных частот. В оставшемся седьмом краевом условии (38) константы A , B , A ₁, B ₁, A ₃, B ₃ , являющиеся в частности и функциями частоты, определены из системы (41) или (42). Однако условие (38) будет выполняться только на дискретном множестве частот to n , n — 1,2,..., [1]. Для их определения необходимо, варьируя частоту ω , добиваться выполнения условия (38).

Отметим в заключение, что в силу различия матриц C — {cj} и S — {sj} в (41), (42) должны различаться и решения этих уравнений, а следовательно, и резонансные частоты для случаев (c) и (s).

ВЫВОДЫ

Таким образом, в работе получен алгоритм определения собственных частот ограниченных упругих цилиндров, заполненных жидкостью. Приведены все необходимые выражения для определения резонансных частот рассмотренного объема. Открытым остался лишь вопрос о правомочности пренебрежения невыполнением краевых условий (12) для напряжений σrz и σzϕ . Этому вопросу, изучению свойств детерминантов матриц C и S , а также практическим расчетам резонансных частот на конкретных примерах будет посвящена следующая статья автора.

Для автоматизации простых, но громоздких вычислений в работе использовался пакет "Ma-thematica-7", лицензия L3259-7547.

Автор выражает благодарность Н.Н. Князькову за постановку проблемы.