Software Module Clustering Using Hybrid Socio-Evolutionary Algorithms

Published Online July 2016 in MECS

Maintenance is the largest and most expensive phase of the software development lifecycle [1]. During this phase, the software system undergoes continuous change and is enhanced for a number of reasons. It is generally accompanied by the turnover of the software engineers involved in its development. It ultimately leads to the decay of the original structure of the system [2]. So, for the effective and efficient maintenance of the software system, it becomes important to re-identify the subsystem boundaries. It might be a difficult task, especially in the absence of original design documents of the software system concerned [3]. If the source code of the software system is the only means available [4], then in order to re-identify the design of the software system, the required Module Dependency Graph (MDG) is built from this source code. Module boundaries in MDG could be defined by grouping sets of related methods, macros attributes and variables into source code files or classes [5]. The relations between the modules could be obtained by extracting the module-level relations from the source code. In a MDG, modules are represented as nodes and the relationships as the edges between these nodes.

Several techniques have been developed to re-identify the design structure of legacy software systems [6].

Software clustering is one such technique that is aimed at categorizing large software systems into smaller manageable subsystems containing modules of similar features. These techniques attempt to identify clusters by analyzing relationships among the modules which could be represented in the form of MDG [7]. The problem of finding the best clustering for a given set of modules is a NP hard search problem. So, we may use search-based software engineering techniques to sort out this problem.

In this paper, we present a novel clustering-based approach to partition legacy software systems. A recently introduced evolutionary optimization strategy, Imperialist Competitive Algorithm (ICA) [8], along with its combination with genetic algorithm (GA) is used to remodularize the software into more manageable clusters to identify the architecture of the system concerned. ICA is a new strategy that is motivated by social and political global search strategies that has recently been found effective in dealing with different optimization tasks [9]. These evolutionary optimization strategies have shown great performance in both convergence rate and better global optima achievement. In this paper, we compare the quality of the software modularization architecture obtained by using this technique with that of the existing GA-based technique. By using t-test, we compare software clustering on the basis of these techniques with that of existing GA-based clustering tools.

The rest of the paper is organized as follows. In Section II, we present related work done in the field of software clustering. In Section III, we present a brief introduction to the problem of software modularization. Section IV and VII deals with ICA-GA and Recursive ICA-GA algorithms (R-ICA-GA) respectively. Quality prediction function TurboMQ and similarity measurement techniques [10-12] to compare the quality of software clustering. In Section IX, we discuss experimental results in a few benchmark un-weighted software systems. Section X is the conclusion and future work in the field is presented.

• II.    Related Work

The maintainability of a software system becomes efficient and effective if the software architecture is well documented. Unfortunately, this kind of documentation may be outdated if software engineers do not consistently maintain it with the changes made [13]. Further, quality of software architectures plays a major role in the success of software thus developed. [14]

In this context, various reverse engineering tools are found to be successful in retrieving the architecture of software system [15-16].The majority of the reverse engineering tools proposed in literature are based on clustering algorithms [17].

One such popular software clustering tool is ACDC [18]. This is a pattern-based software clustering technique that recovers subsystems using the incremental clustering technique. In this technique, a structure is created on the basis of patterns between subsystems and each newly introduced resource is placed in the subsystem which seems most appropriate.

Another popular tool, Bunch [19], attempts to find a decomposition that optimizes a quality measure called TurboMQ which is based on high cohesion and low coupling. It is a popular tool based on search-based techniques like hill climbing and GA etc. In this paper, we compare results obtained by our approach with that of this tool.

Harman et al. [16] modified GA approach implemented in BUNCH by proposing a novel encoding and crossover operator. This technique modified existing way of using GA by allowing only one representation per modularization. This new crossover operator outperforms the traditional one, but it gets trapped at local optima very often.

In a recent work [20]; the authors used cooperative clustering based on MQ for software Clustering. It has been observed that this approach leads to degraded performance with increase in size of the problem. Particle Swarm Optimization (PSO) algorithm has also been used for the cause of software clustering [21] using MQ as objective for optimization.

In this work use of Imperialistic Competition Algorithm (ICA) and its hybrids have been investigated for the cause of software modularization. ICA has been used for synchronization of chaotic systems based on an intelligent controller which based on brain emotional learning (BELBIC) [22].

• III.    Problem Statement

As mentioned above, optimization techniques have been applied to several software engineering activities including maintenance. In this paper, we use the recursive combination of evolutionary algorithms, ICA and GA (RICA-GA) [23], and compare their performances to the well-known evolutionary algorithm GA [24]. It is observed that the recursive combination of ICA and GA leads us to find the best modularization of the software that is found to be much more similar to the original design documentation; hence, it is found to be more effective.

The goal of our approach is to partition a MDG of the source-level entities and relations into a set of clusters, such as clusters that represent partitioned subsystems where highly-interdependent modules (nodes) are grouped in the same subsystems (clusters). The MDG we are using in this paper has been widely used by researchers [11, 25], therefore it becomes easy to compare our approach to that of other studies of metaheuristic search algorithms. Table 1 shows the list of software systems whose MDGs are used in this paper [26]. The original design structure (as obtained from its documentation) of one of these software systems, called Mini-Tunis, is shown in Fig. 1.

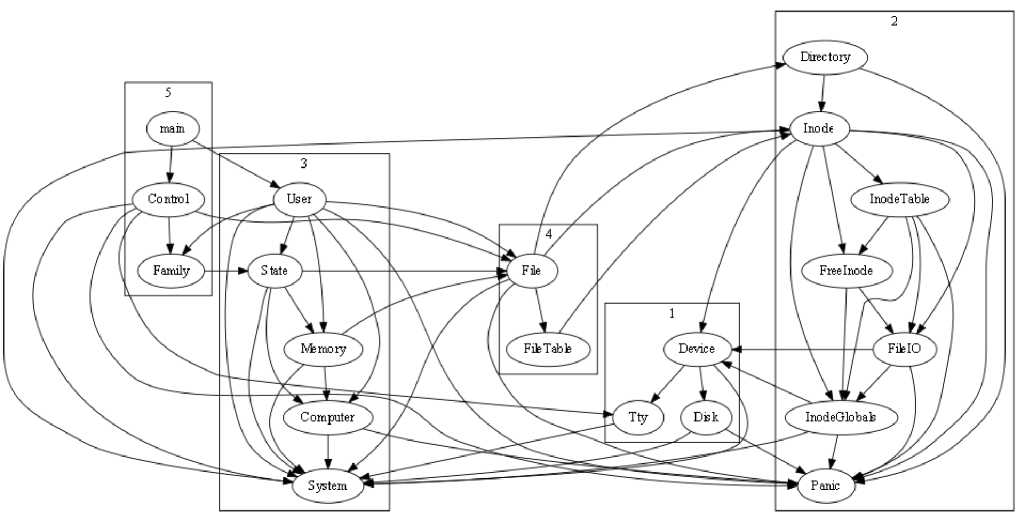
Fig.1. Structure of Mini-Tunis as described in original design specification

• IV.    Imperialist competitive Algorithm

This algorithm is used for optimization and is inspired by the imperialistic competition [8]. It begins with an initial population. Population individuals (called country) are of two types: colonies and imperialists. Together they form empires. Imperialistic competition among these empires is the basis of the evolution in this algorithm.

This algorithm uses the assimilation policy. Based on this policy, the imperialists try to improve the economy, culture and political situation of their colonies (also called their empire).

Table 1. Description of software systems to be used

Software System	Modules in MDG	Edges in MDG	System Description
Rcs	29	163	Open source version control tool
Mini-Tunis	20	57	A  simple  operating system
Ispell	24	103	An open source spell checker
Boxer	18	29	A drawing tool
Bison	37	179	Parser generator
Grappa	74	112	Graph    visualization and drawing tool

The power of an empire depends on the power of its imperialists and its colonies. The imperialists that are weaker lose their colonies and join a more powerful empire for greater support. In the end, the weak empires collapse and only one powerful empire is left. This final empire is the result of optimization.

The main steps of ICA are summarized in the flowchart shown in Fig. 2.

• A.    Creation of initial empires

The initial population of ICA is created randomly. Each member of this population is a vector of random numbers which is called a country. The cost of objective function (also called its fitness value in GA) is calculated for each of these countries and is preferred to be a minimum. The colonies are required to be proportionally divided among imperialists. Imperialists with a lot of power will be associated with a large number of countries.

With respect to software clustering, let us see how we define a country. Each node in the MDG has been assigned a unique numerical identifier. These identifiers define the position of the node in the encoded string. The encoded string defines the cluster that each node has been assigned to. So, if we have a graph with n number of nodes, then a country is defined as s1,s2,....sn where each si is the label of the module or cluster to which the node has been assigned.

The job of ICA is to find the optimal solution to the problem; the solution with the least cost value.

TurboMQ is a function (Mitchell and Mancoridis, 2002) that is found to be quite efficient and effective for measuring the cost of each country and, hence, the quality of software clustering. In this function, interconnectivity and intra-connectivity are measured independently.

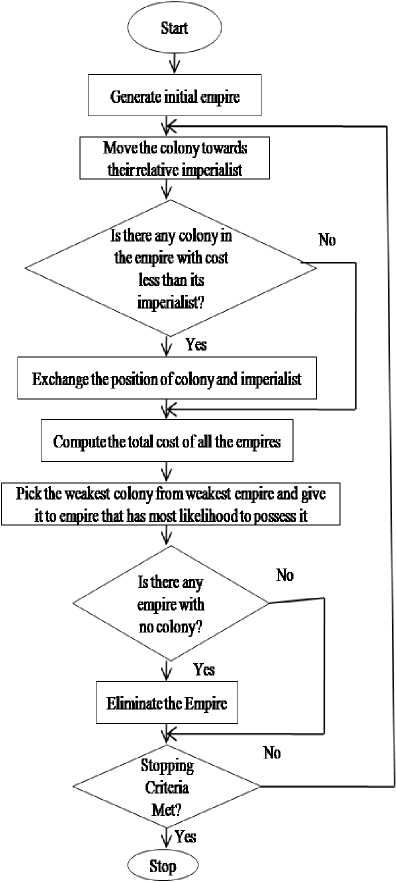
Fig.2. Flowchart of Imperialist Competitive Algorithm

Intra-connectivity (cohesion)

Intra-connectivity (A) measures the degree of connectivity between components that are grouped in the same cluster. A higher value of A indicates good partitioning whereas a lower value of A indicates low degree of intra-connectivity, and hence, poor subsystem partitioning. Therefore, intra-connectivity for cluster i could be calculated as Eq. (1).

Ai=μi/Ni2

N :Number of components          (1)

μ :Intra-edge depnendencies

Inter-connectivity (coupling)

Inter-connectivity (E) measures the degree of connectivity between two distinct clusters. The larger the number of interdependencies means the larger the difficulty in maintenance. This is because changes to a module may affect many other parts of the system due to the subsystem relationships. Inter-connectivity Eij between clusters i and j is mentioned in Eq. (2).

Eij = 0 if i=j

Eij = = ij (2NiNj ) ifi * j

N : Number of components in module i

N : Number of components in module j

ɛ_i j : Inter edge dependencies

0 ≤ E ij ≤ 1

E ij is 0 when there are no module-level dependencies between module i and module j.

E ij is 1 when each module in subsystem i depends on all of the modules in subsystem j and vice-versa.

The Turbo MQ measurement for an MDG partitioned into k clusters is calculated by summing the Cluster Factor (CF) for each cluster.

CF = 0 if g_z = 0  _k

CF- = ^ / 2 ^ +   S   (s^ + s ■ _z) otherwise (3)

k  j = 1, i * j

TurboMQ = Z CF

As we need a system with maximum cohesion and minimum coupling, the cost function TurboMQ should have maximum value. It means the higher the value of TurboMQ, the better the quality of the partition. On the other hand, ICA and GA works on the principal of cost minimization. This means it selects the partition with the minimum value of objective function. Therefore, in order to use TurboMQ (maximization function) as objective function in ICA and GA (minimization-based), we use negation of TurboMQ (-TurboMQ) as cost minimization function. This means if ICA or GA selects partition with minimum value of –TurboMQ, it is actually selecting a partition with the highest value of TurboMQ i.e. the clustering of best quality.

• B.    Assimilation: movement of colonies toward the imperialist

In ICA, the assimilation process is modeled by moving all of the colonies toward the imperialist along different optimization axis. Fig. 3 shows this movement. Continuation of assimilation will cause all of the colonies to be fully assimilated into the imperialist. In this figure, x is a random variable with uniform distribution. The value of x lies in the range as shown in equation x ~ U(0, eXd)

where β (also called AssimilationCoefficient) is a number greater than one, and d is the distance between the colony and the imperialist state. β >1 causes the colonies to get closer to the imperialist state from both sides. The most appropriate value for β is found to be 1.5.

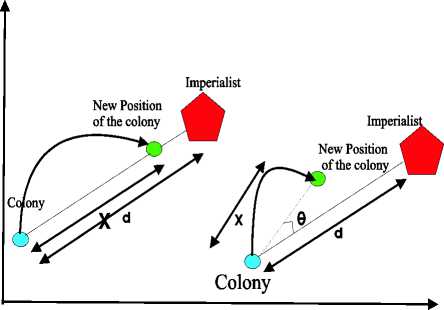
Fig.3. Moving colonies toward their relevant Imperialist

Assimilating the colonies by the imperialist states does not result in direct movement of the colonies toward the imperialist. So a random amount of deviation θ is added to the direction of movement to increase the ability to search more area around the imperialist (as shown in Fig. 3). In this figure, θ is a parameter with uniform (or any proper) distribution as shown in equation below

0 ~ U( -у , у )

where γ (also called AssimilationAngleCoefficient) is a parameter that adjusts the deviation from the original direction.

It is found that for the software systems under consideration, the values of 3π/4 (Rad) for γ results in good convergence of countries to the global minimum.

• C.    Exchanging positions of the imperialist and a colony

While moving toward the imperialist, a colony might reach a position with cost lower than the imperialist. In this case, the imperialist and the colony change their positions. The algorithm then continues with the imperialist in the new position. Total power of an empire can be calculated as shown in equation 8.

TCn = Cos t ( imperialistn ) + Z Cos t ( colonies _ of _ empiren )

where TC n is total cost of the nth empire and ζ is a positive small number.

Value of ζ influences the total power of the empire. If it is a small value then the total power is determined by just the imperialist, and increasing it will increase the role of the colonies in determining the total power of an empire. The value of 0.05 for ζ has shown good results in most of the software systems under consideration.

• D.    Imperialistic competition

It is a main part of ICA and is expected to cause colonies to converge at global minimum cost. All empires try to take the possession of colonies of other empires. The weaker empires start combining with powerful empires.

The process of selecting an empire is similar to the roulette wheel approach for selecting parents in GA. But this method of selection is much faster than the roulette wheel because cumulative distribution function is not required to be calculated. This is the main reason for better behavior of ICA. As a result, the execution speed of the algorithm increases, leading to earlier convergence. More information and its Matlab code are available at The re-modularized design structure obtained automatically after the application of ICA is shown in Fig. 4.

• V.    Genetic Algorithm

GA is created on the basis of Darwin’s theory of evolution. For a specific problem, it randomly defines an initial population of individuals called chromosomes that represent a part of the solution space of the problem. Next, on the basis of the value of fitness value (objective function), the individuals are selected in a competitive manner. The genetic search operators such as selection, mutation and crossover are then applied one after another to obtain a new generation of chromosomes in which the expected quality over all the chromosomes will be better than that of the previous generation. This process is repeated until the termination criterion is met, and the best chromosome of the last generation is reported as the final solution [27]. A step by step procedure for the same is shown in Fig. 5.

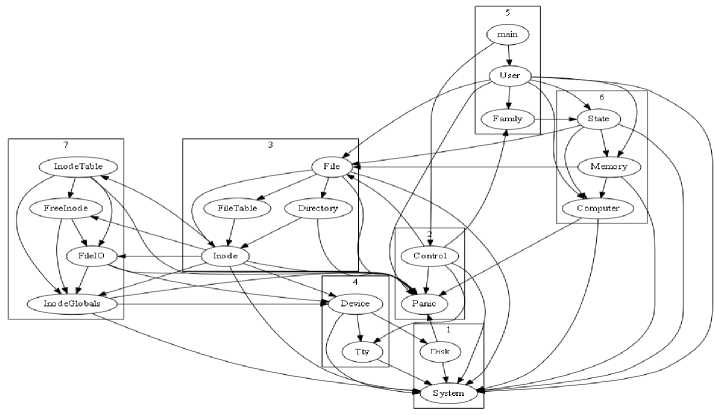
Fig.4. Structure of Mini-Tunis as described by ICA

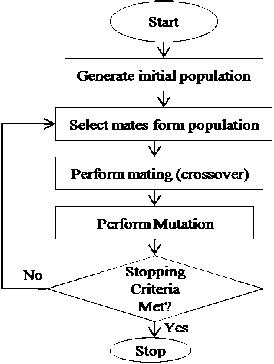
Fig.5. Flowchart for GA

• VI.    ICA-GA

In this technique, ICA is used to optimize the cost function and identify the optimum software clusters. The resulting software clusters obtained are used as the initial population of GA. The flowchart for the same is shown in

Fig. 6. Flowchart for GA is shown in Fig. 5. The parameters and their most appropriate values obtained by repeated execution of these algorithms are shown in Tables 2 and 3. The re-modularized design structure obtained automatically after the application of GA and ICA-GA are shown in Fig. 7 and 8.

Table 2. Parameters for GA

Number of generations	200
Population size	200
% of cross-over	60
% of mutation	2

Table 3. Parameters for ICA

Number of generations	200
Number of countries	200
Number of imperialists 10% of countries	20
Assimilation coefficient β	2
AssimilationAngleCoefficient	0.5
Zeta ξ	0.1

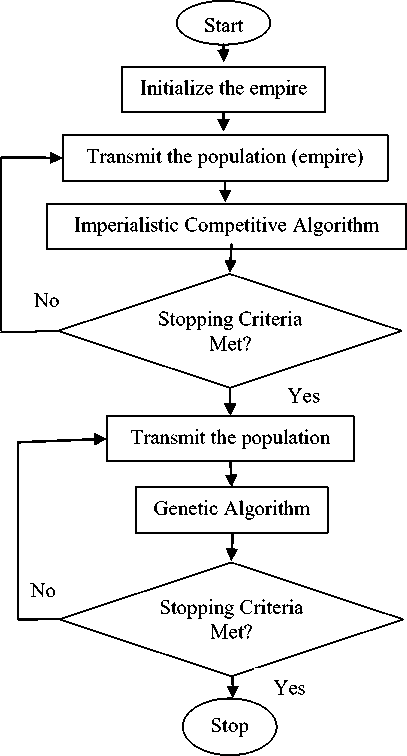
Fig.6. Flowchart for ICA-GA

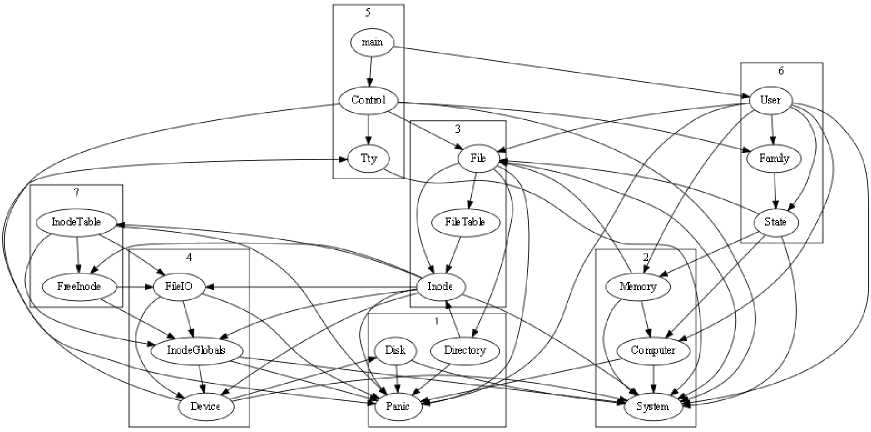
Fig.7. Structure of Mini-Tunis as described by GA

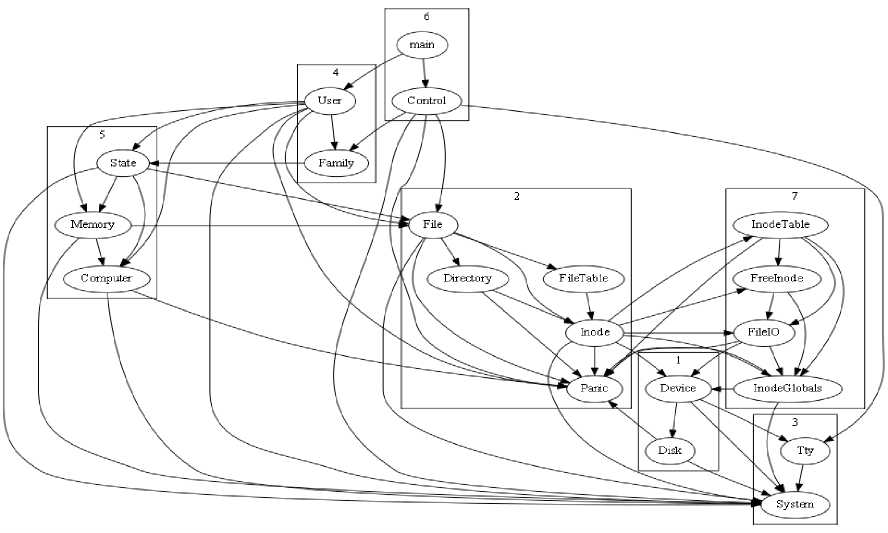
Fig.8. Structure of Mini-Tunis as described by ICA-GA

• VII.    Recursive ICA-GA

In another approach, the two basic algorithms ICA and GA are applied recursively one after another until some stopping criteria is met. The required parameters and their most appropriate values obtained by repeated execution of these algorithms are shown in Tables 2 and 3. GA avoids the concentration of countries near imperialists. On the other hand, ICA always sends the colonies toward the imperialists and mainly concentrates on the populations near the imperialists. The flowchart for this technique is shown in Fig. 9. The global optimum is usually near the local optimums in most of the problems.

So, the populations which are concentrated near the imperialists of ICA (which may be near the global optimum), will expand and tremble by recursive combination of these two algorithms. This algorithm is based on ICA and takes the help of GA to expand the populations of colonies which are concentrated near the imperialists [23]. This combination leads to a fast decrease in the convergence curve and increase in the quality of resultant clusters obtained. The re-modularized design structure obtained automatically after the application of ICA is much more similar to original design structure and is shown in Fig. 10.

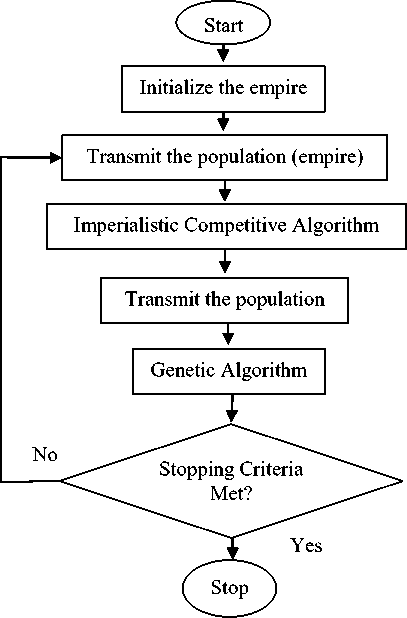
Fig.9. Flowchart for Recursive ICA-GA

• VIII.    Similarity Measure

Over the past few years, several clustering techniques have been presented in literature that leads to efficient system decomposition. The effectiveness of these clustering techniques must be measured. One way to measure it is to identify similarity between the resulting modularization and original design or between two different decompositions of the same system.

In order to accomplish this, the authors [28] identify the similarity between decompositions by considering how much a module depends on other modules in its subsystem, as well how much it depends on the modules of other subsystems. They found measures EdgeSim and MeCl which present both a similarity and a distance measurement that ranks the individual differences between the decompositions, and applies an appropriate weighted penalty to each disagreement.

• IX.    Experimental Results on Software Graphs

The technique was tested on a large number of software systems. The proposed methods have been applied on a large number of software systems and compared with the well-known Bunch tool Said known work done was based on heuristic search algorithms that automatically cluster the source code into subsystems. It has been observed that the recursive ICA-GA re-modularized software systems into partitions much more similar to original design architecture. The parameters required are set to values shown in Tables 2 and 3. In order to show the improvement in terms of convergence speed and efficient clustering, we show the result of the experiment on five popular software systems described in Table 1. Fig. 11 and 12 show the minimum and average fitness of software system 'Mini-Tunis' on the execution of GA,

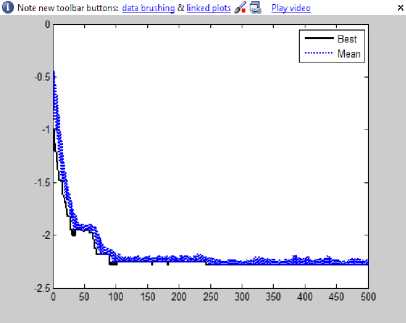
ICA, ICA-GA and R- ICA-GA respectively. These plots demonstrate that R-ICA-GA converges at a very early stage and execution time of the algorithm is smaller than the others. Along with it, the value of fitness function or cost of the final empire comes out to be higher than the other earlier algorithms which mean a better clustering output. In order to compare the clustering output of all these algorithms for Mini-Tunis, we calculate EdgeSim and MeCl values to compare similarity of clustering of all of these algorithms with respect to original design documentation. The values thus obtained are shown in Table 4. This table illustrates that the algorithm R-ICA-GA results in the output most similar to that of original design structure. It is depicted by the highest value of EdgeSim and MeCl metrics for Recursive ICA-GA. Along with this, the same is obtained by R-ICA-GA in least number of epochs. Similarly, the output of other software systems after repeatedly executing these algorithms is summarized in Table 5 and 6. By close evaluation of Tables 5 and 6, it depicts that although ICA takes much more time to converge as compared to GA, the quality of resulting cluster is better (overall cost is higher) than the earlier available tool bunch. When compared to ICA-GA, the quality improves further. In the case of R-ICA-GA, the result shows much higher quality as well as much less convergence time; hence, it is found to be the best of all the above combinations.

Table 4. Clustering output of algorithms for Mini-Tunis using EdgeSim and MeCl

Algorithm	EdgeSim	MeCl	Overall cost/ fitness values	Generations used to converge
GA	71.9298	40	-1.9980	52
ICA	61.4035	5	-2.1573	2400
ICA-GA	77.1930	65	-2.2268	51
R-ICA-GA	68.4211	60	-2.2866	70

Table 5. Clustering output (mean and mode) of algorithms for various software systems

Software System	Mean				Mode
	GA	ICA	ICA-GA	R-ICA-GA	GA	ICA	ICA-GA	R-ICA-GA
Ispell	-2.2600	-1.9456	-2.2254	-2.3305	-2.3784	-2.3364	-2.3708	-2.3697
Boxer	-3.0447	-2.9360	-2.9966	-3.1011	-3.1011	-3.0639	-3.1011	-3.1011
Bison	-2.4594	-1.7309	-2.2963	-2.6828	-2.5123	-2.2700	-2.5464	-2.7234
Grappa	-13.9035	-9.3913	-13.7490	-17.0071	-15.6346	-12.2182	-15.7460	-18.3984
MiniTunis	-2.1533	-1.6614	-2.1940	-2.2897	-2.2254	-2.1642	-2.2406	-2.3145

Table 6. Clustering output (maximum value and standard deviation) of algorithms for various software systems

Software system	Maximum				Standard deviation
	GA	ICA	ICA-GA	R-ICA-GA	GA	ICA	ICA-GA	R-ICA-GA
Ispell	-2.2739	-2.2348	-2.2824	-2.2952	0.0707	0.1719	0.1171	0.0330
Boxer	-2.3784	-2.3364	-2.3708	-2.3885	0.1014	0.1380	0.1211	0.0665
Bison	-3.1011	-3.2545	-3.1011	-3.1011	0.0831	0.1980	0.1549	0
Grappa	-2.6709	-2.4455	-2.5464	-2.7474	0.1298	0.2312	0.1816	0.0640
M-Tunis	-15.6346	-13.6062	-16.0569	-18.4226	0.8185	1.5591	1.1269	1.2316

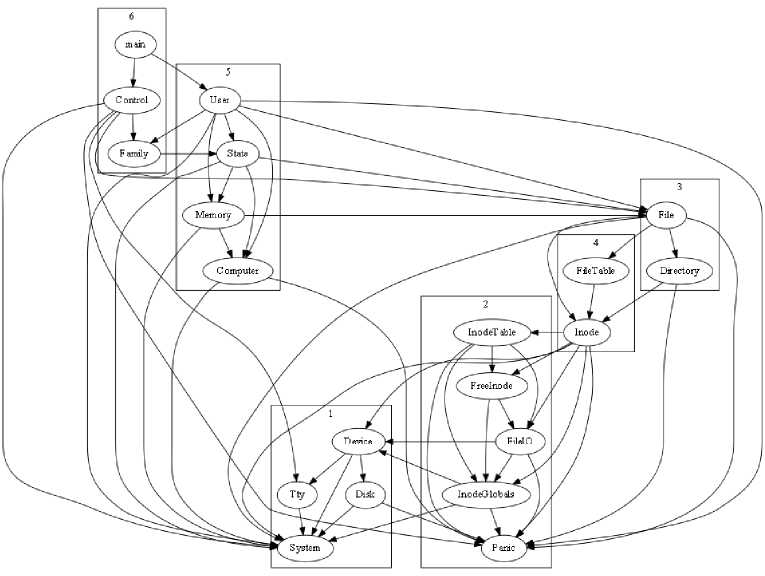
Fig.10. Structure of Mini-Tunis as described by Recursive ICA-GA

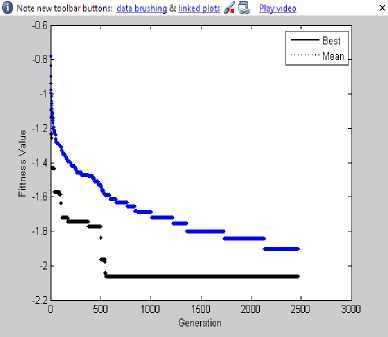
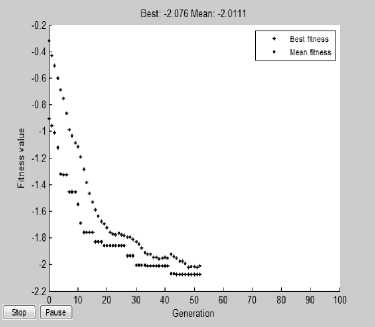
Fig.11. Minimum and average fitness of software system Mini-Tunis on the execution of ICA and GA

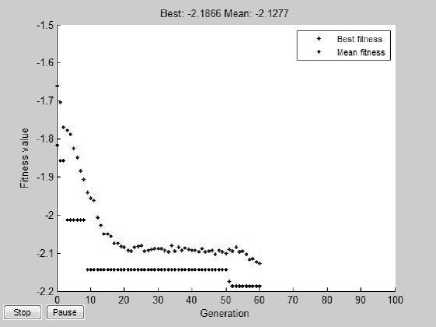
Fig.12. Minimum and average fitness of software system ‘Mini-Tunis’ on the execution of ICA-GA and Recursive ICA-GA

• X.    Conclusion and Future Work

This paper contributes to the field of reverse engineering by using the combination of meta-heuristic search-based techniques ICA and GA to solve the software clustering problem. This work to cluster the structure of large, real world software systems is efficient and useful especially in the absence of original design documentation. The automatic clustering technique generates better and faster results. This approach is useful to software maintainers as it quickly partitions the software system using the resource dependencies specified in the static structure of the source code.

In this paper, the four evolutionary optimization algorithms ICA, GA, ICA-GA and R-ICA-GA were used to reverse engineer the software system. All of the named algorithms are compared to each other in a number of generations needed to converge and quality of the clusters is obtained. Results show that the Recursive ICA-GA is the best algorithm among these four algorithms for reverse engineering.

A encoding of the country has an impact on the quality of the clustering. So we can use some other better encoding scheme to further improve the results.

Acknowledgment

The authors are grateful to Spiros Mancoridis for providing both the Bunch tool and the MDGs used in this paper. We are also pleased to thank Mr. Harjit Singh, senior consultant, Tata Consultancy Services, New Delhi and Pavneet Kaur, component design engineer, Intel Corporation, USA, for their able guidance and useful suggestions.