Software Testing Resource Allocation and Release Time Problem: A Review

Published Online February 2014 in MECS

Software is becoming essential to every aspect of our life. Some software systems such as nuclear power plant control systems, medical support systems, and power distribution systems are life critical. Developing extremely reliable software has become essential. Software producers must guarantee the satisfactory reliability of the delivered software product, the time of delivery and its cost. Since development and the operational costs of software is increasing. Therefore the cost and schedule pressures faced by companies, it is quite difficult to create software products that simultaneously provide high reliability, rapid delivery and low cost. The need for trade-offs is essential and the characteristics of the software must be carefully selected. Many systems are now divided into a component that is developed by different companies. A definite need exists for the clear identification of the characteristics of these components as well as those of the whole system.

Software development begins with requirement specifications and analysis to decide the services that the system should provide and meets all the requirements. Next step is to design of software, their functionality, and also to identify the associations between them. Often, the modules can be purchased from the open market or can be developed in house. When a module is developed in house, the specific method chosen for implementation must be determined for example, an internal sort module can be implemented using merge sort, bubble sort, selection sort, radix sort, quick sort, etc. Once the system is designed, implementation can be performed. It involves detailed design, coding and unit test of programming tasks, as well as a process of integrating separately tested code that may include purchased modules until the whole system is integrated and tested. The application of computer software has progressively become ubiquitous and worldwide. Many software application systems are responsible for critical services, such as weapon systems, air traffic control systems, payment systems etc. Due to the importance of software application, proficient testing of software becomes an even more important. During testing, engineers should exercise the program with specified test cases couple of times so as to remove the detected faults and realize bug free software. However, testing resources are limited and Project managers need to determine when to stop testing and have to make an interim risk evaluation and management (E/M). Actually, software risk management is a software engineering practice with tools, methods, and processes for managing risks in a software project. While some risk assessment techniques advocate assigning quantitative probabilities for perceived likelihood, in practice it is very difficult for us to agree on the subjective numbers. In general, risk involves two characteristics: uncertainty and lost. Risk management is concerned with identifying risks that may affect the project and planning to ensure that the risks do not develop into major threats [1]. Thus, we can clearly see that the risk exposure is mainly dominated by the probability of an unsatisfactory outcome. In fact, we can easily relate such ideas to software reliability modeling and analysis. Software reliability is the probability that the given software shall be functioning correctly under given environment during a specified period of time [2-4]. It is a key component of software quality and can be used for planning and controlling all testing resources during development. Besides, it can also give us a confidence about the correctness of software. Many software reliability growth models (SRGMs) has been developed over past three decades [2-5]. SRGMs can be used to evaluate software development status and software reliability engineering technology quantitatively. The quantified data can greatly benefit the software release time management. However, the motive for exercising software dominates the set of inputs into program evaluation. The fault detection and operation phenomenon of the software in the operational phase are different from those in the testing phase.

The rest of this paper is organized as follows. Sections 2 describe optimization problems in software reliability. Sections 3 describe the detailed review Section 4 concludes the paper and section 5 about the future work.

• II.    Optimization problems in software reliability

Commercial software development company, enhanced complexity of products, shortened software development life cycles, lesser production costs, scarce resources and higher customer satisfaction of quality have placed a major responsibility on the management to have a closer look on their decision making strategies, future prediction and analysis in the areas of software debugging, testing and verification. The available resources are needed to be allocated efficiently without compromising with their effectiveness. Optimization Techniques play a significant role to help policy planners, managers and administrators in the analysis of many complex decisions or allocation problems. It offers an indispensable degree of operational simplicity. Skill in modeling to capture the essential elements of a problem and good judgment in the interpretation of results are required to obtain meaningful conclusions. During the testing phase of SDLC, the management of company faces the two major problem one is how to allocate the available resources and second when to release the software. Fig. 1 illustrates the overall scenario of optimization problems in software reliability.

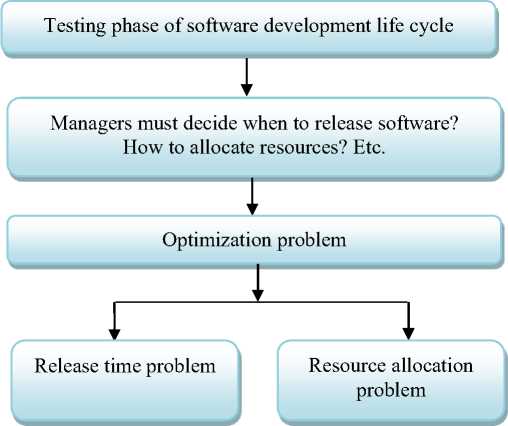
Fig 1: Overview of Optimization Problems in Software Reliability

• A.    Release Time Problem

It owes to the prevailing paradox that software user’s requirements are conflicting with the developers. Software users demands quicker deliveries, cheaper software and superior quality product whereas software developer’s aim at maximizing the profit margins, minimizing their software development cost and meeting the competitive requirements. A crucial decision problem that the management encounters is to decide when to stop testing and release the software system to the customers such kind of problem is recognized as “Software Release Time Problem”. If the release of the software product is extremely delayed, the manufacturer may suffer in terms of penalties and revenue loss, while a premature release may cost heavily in terms of fixes (removals) to be done after release that consequently may harm the manufacturer’s reputation. The optimization problem of determining the optimal time of software release may be formulated based on goals sets by the management in terms of software development cost, product reliability and failure intensity etc. subject to the system constraints. Fig. 2 describes the classification of software release time problems.

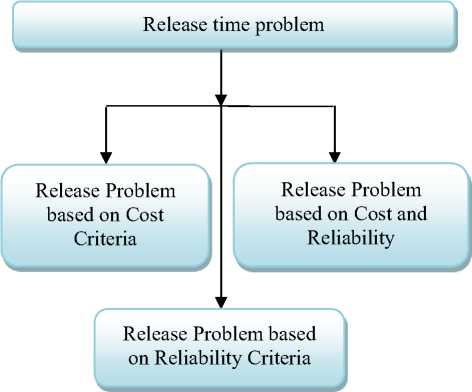
Fig 2: Classification of release time problem.

• B.    Resource Allocation Problem

Allocation of testing resources is a difficult issue. Sometimes it is difficult to justify testing in projects, especially small ones. We know that testing is necessary to guarantee product quality. Management knows the importance of testing and how the test protects the organization and their products from embarrassing failures. This persuades the management to allocate testing resources optimally so that the desired reliability of the software can be achieved by removing maximum numbers of faults. This type of optimization problems is identified as “Resource Allocation Problem”. Fig 3 illustrates the resource allocation problem in software reliability.

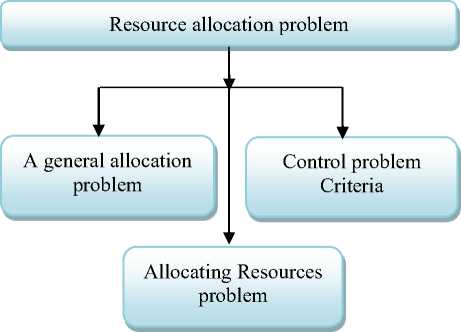
Fig 3: Classification of Resource allocation problem.

• III.    Review

The development of high superiority software satisfying cost, a schedule and resource requirement is a vital prerequisite for improved competitiveness of any organization. One major difficulty to master this challenge is the inevitability of defects in software products. The testing of software systems are focusing to strong conflicting forces. One of the most effective ways to do this is to apply software reliability engineering during testing and development phase. Software reliability engineering delivers the desired functionality for a product much more efficiently by quantitatively characterizing its expected use. The software reliability engineering tends to increase reliability while decreasing software development time and overall cost. Thus software reliability engineering balances customer needs for the major quantitatively measurable quality characteristics of reliability, availability, delivery time and life cycle cost more effectively. In the literature, several researchers have developed models for cost benefit analysis of the testing process, all based on the initial cost model described by [6]. [7] developed and solved two resource allocation problems for modular software, minimizing the total number of remaining faults in the software modules when the amount of available testing resources is previously specified and vice versa. [8] Studied the allocation problem minimizing the mean number of remaining faults in the software modules with a reliability aspiration and budget constraint. [9] Determined the optimal amount of resources needed for software module testing using the hyper-geometric software reliability growth model.

• [10]    Discussed resource allocation problem to maximize the total fault removal from software consisting of several independent components. For the resulting optimization problem, they demand marginal testing effort function (MTEF), where the testing resource consumption was represented in terms of fault removal. [11] Discussed dynamic programming approach to testing resource allocation Problem for modular software in this Two Optimization models are proposed for optimal allocation of testing resources among the modules of Software. In the first model, authors maximize the total fault removal, subject to cost Constraint. In another model, other constraint representing aspiration levels for fault removals for each module of the software is added. Authors solved this models using dynamic programming technique. A dynamic programming approach for finding the optimal solution has been proposed. The methods have been already illustrated through numerical examples. Further [12] studied various resource allocation problems maximizing the number of faults removed from each module under constraint on budget and management aspirations on reliability for exponential and S-shaped SRGMs [6,13,14]. They have discussed mathematical, dynamic and goal programming approaches to yield solutions of such class of optimization problems. [15] Also solved resource allocation problem maximizing the number of faults removed from each module under constraint on budget.

• [16]    Investigated an optimal resource allocation problem in modular software systems during testing phase. The main goal is to minimize the cost of software development when the number of remaining faults is to minimize and a desired reliability objective is given. Authors analyzed the sensitivity of parameters of proposed software reliability growth models. In addition,

they also see the impact on the resource allocation problem if some parameters are either overestimated or underestimated. Authors evaluated the optimal resource allocation problems for various conditions by examining the behavior of the parameters with the most significant influence which have been stated by solved numerical example.

• [17]    Considers two kinds of software testing resource allocation problems. The first problem is to minimize the total number of remaining faults, given a fixed quantity of testing-effort, and a reliability objective. The last problem is to optimize the amount of software testing effort given the total number of remaining faults in software, and a desired reliability objective. Author has also proposed several strategies for module testing to help software project managers to solve these problems, and make the best decisions. Author provides several systematic solutions based on a nonhomogeneous Poisson process model (NHPP) model, allowing efficient allocation of a specified amount of testing resource expenditures for each and every software module under some specified constraints. Author also describes numerical examples on the optimal testing resource allocation problems and performed sensitivity analysis.

• [18]    In this paper, ensemble models are developed to correctly estimate software reliability. Three linear ensembles and one non-linear ensemble are planned and tested. Based on the experiments conducted on the software reliability data obtained from research paper, it can observe that the non-linear ensemble outperformed all the other ensembles. Both theoretical and empirical works indicate that ensemble can be an effective and efficient way to improve accuracies. [19] Discussed an idea of genetic algorithm used in software reliability. The reliability of software systems is essentially a mathematical programming problem composed by the corresponding objective function and restriction constraints two parts. The problem is usually with a large number of local extreme points and often is no differentiable, discontinuous, multi-dimensional, highly nonlinear combinatorial optimization problem. Therefore, to accurately solve the global optimal solution is generally difficult. Traditional solving algorithm can’t obtain satisfied global optimal solutions. The genetic algorithm is applied once again in the reliability of software systems for the global optimization distribution of the reliability indicators. Comparing with the traditional software reliability allocation techniques, genetic algorithm has shown good results in the solving process of searching for optimal allocation schemes. At the same time, the reliability distribution of the software system is essentially a type of combinatorial optimization problems with constraint conditions, and relative to the traditional solving methods, genetic algorithm can display a better performance.

• [20]    Formulated an optimization problem to allocate the resources among different modules under an assumption that change point is generated in each module by design due to change in testing strategy, running environment, defect density or testing skill maturity such

that the total fault removal is maximized while incorporating the effect of both types of imperfect debugging. Also, a correct Understanding of modular system cannot be attained without giving a prime concern to the accurate effect of each module on the overall performance. The weightage of each and every module will be specified. This relative importance in this work is obtained using Analytical Hierarchy Process (ARP). Author has also considered the problem of determining minimum requirements for the testing resources so that a desired proportion of faults are removed from each module.

• [21]    Discussed to solving Optimal Testing Resource Allocation Problems OTRAPs with Multi-Objective Evolutionary Algorithms (MOEAs). Specifically, author formulated OTRAPs as two types of multi-objective problems. First, consider the reliability of the system and the testing cost as two objectives. Second, the total testing resources used is also taken into account as the third objective. The benefits of MOEAs over state-of-the-art single objective approaches to OTRAPs will be shown through empirical studies. This study has revealed that a well-known MOEA, namely No dominated Sorting Genetic Algorithm II (NSGA-II), performs well on the first problem formulation, but fails on the second one. Author did experimental study and compared MOEAs with Single-Objective Approaches and Harmonic Distance Based Multi-Objective Evolutionary Algorithm (HaD-MOEA) With NSGA-II on Hence, a Harmonic Distance Based Multi-Objective Evolutionary Algorithm (HaD-MOEA) is proposed.

• [22]    Formulated an optimization problem in which the total number of faults removed from modular software which includes simple, hard and complex faults. Author developed model for simple faults, hard fault and complex fault. As follow

Modeling Simple Faults: Simple faults are the faults which can be removed instantly as soon as they are observed. The mean value function for the simple faults of the software reliability growth model with respect to testing effort expenditure can be written as

Modeling Hard Faults: The hard fault takes more testing time for the removal. This means that the testing team will have to spend more time to analyze the cause of the failure and therefore requires greater time to remove them.

Modeling Complex Faults: These faults require more testing time for removal after isolation as compared to hard fault removal. Hence they need to be modeled with greater time lags between failure observation and removal.

Authors maximized the model subject to budgetary and reliability constraints. Then for solving the optimization problem author have used genetic algorithm. A numerical example has been discussed to illustrate the explanation of the formulated optimal effort allocation problem.

• [23]    Proposed optimal resource allocation to minimize the software cost during testing and operational phase using optimal control theory.

• [24]    Discussed Resource control and resource maintenance during the software testing is one of the

finest optimization problems. During the software testing many of the resources like time, effort and budget are consumed. The main work of the manager is to allocate the resources in a constrained manner such that the effort can be optimally allocated and overall budget is minimized. In this paper author proposed an imperfect debugging SRGM during testing and resource allocation is done based on optimizing the effort and reliability. Author used two testing resource allocation schemes one by minimizing the number of remaining faults and allocating the resources to attain the maximum reliability. An experimental result also shows the proposed model well fitted for software testing.

• [25]    Have studied optimal software release problems considering the host concentrated software development process.

• [26]    Used a neural network technique to deduce the optimal software release timing which minimizes the appropriate cost criterion via artificial neural networks. [27] Discussed the sequential software release policy based on a state space model, considering a Gamma– Gamma-type invariant conditional distribution to defining the state space model. [28] Presented a software cost model that is used to formulate total software cost projects and discussed the optimal release policy based on reliability and cost, considering total testing effort and efficiency. [29] Studied the discrete cost optimal software release policy based on the generalized discrete binomialprocess model.

• [30]    Formulated a mathematical programming model which, for a given level of software reliability, determines module reliabilities by minimizing development and testing costs. [31] Presented a software reliability allocation model. In their model the reliability

of a program is the multiplication of the reliability of its modules, and the reliability of the system is a weighted sum of the reliability of its programs. The overall cost of each and every module is supposed to be a linear function of its reliability. The goal of the model is to and the reliability of each module so that the reliability of the system will be maximized without exceeding a given budget. They also proposed extending the model by making cost an exponential or a logarithmic function of reliability.

[32, 33] have proposed optimal released policy for module based software. [34] Investigated software release policies to minimize development cost while satisfying a reliability objective in dynamic environment. [35] Proposed a two-dimensional software reliability growth model which takes into consideration both these factors in predicting number of faults removed from software. Authors used Cobb Douglas production function to develop the mathematical model. Further, the proposed two dimensional modeling frameworks are applied for determining optimal allocation of resources and testing time simultaneously to a modular software system. Author investigated such as two dimensional optimization problem which assigns testing time and manpower resources among the modules so that the total software development cost is minimized under the constraint of achieving pre-defined proportion of faults removal from each and every module. In order to resolve the formulated allocation problem a two dimensional genetic algorithm (GA) is used. Authors assumed that the model is developed under the perfect debugging environment and also a numerical example is presented to illustrate the formulation and solution of the allocation problem.

Table 1. IMPORTANT SUMMARY ABOUT THE REVIEWS.

Author	Technique Used	Highlights
1
H. Ohetera, and S.Yamada [7]	Developed     mathematical model	Solved resource allocation problems for modular software, minimized the total number of remaining faults in the software modules when the amount of available testing resources is previously specified.
R. Huo, S. Kuo and Y.Chang [9]	Hyper-geometric    software reliability growth model	Studied the allocation problem minimized the mean number of remaining faults in the software modules with a reliability aspiration and budget constraint.
P.K.Kapur,   P.C.   Jha,   and AK.Bardhan [11]	Dynamic     programming approach	Maximize the number of faults removed from each module under constraint on budget and management aspirations on reliability for exponential and S-shaped SRGMs
M. Khan, N. Ahmad, and L.Rafi [15]	Dynamic     programming approach	Solved resource allocation problem minimized the number of faults removed from each module under constraint on budget.
N. Raj Kiran and V. Ravi [17]	Soft computing techniques	Two kinds of software testing resource allocation problems. The first problem is to minimize the total number of remaining faults given a fixed quantity of testing effort, and a reliability objective. The last problem is to optimize the amount of total software testing effort given the number of remaining faults, and a reliability objective.
Kapur, P K, Anu G Aggarwal and Gurjeet Kaur [20]	Genetic Algorithm	Optimal allocation for testing resource for modular software.
Zai Wang and Ke Tangand Xin Yao [21]	Multi objective approach	First, authors considered the reliability of the system and the testing cost as two objectives. Second, the total testing resources used is also taken into account as the third objective.
P.K. Kapur et al. [23]	Optimal control theory	optimal resource allocation to minimize the software cost during testing and operational phase
Dohi, T., Nishio, Y., and Osaki and S [26]	Artificial Neural Networks	Optimal software release timing which minimizes the appropriate cost criterion
Chiang and Mookerjee [27]	learning curve phenomenon	discussed the sequential software release policy based on a state space model
Jain, M. and Priya, K [32]	Mathematical Model	Solved software release problem to minimize development cost while satisfying a reliability objective in dynamic environment.
P. K. Kapur, Anu G. Aggarwal and Gurjeet Kaur [35]	Developed model using Cobb Douglas production function	Two-dimensional software reliability growth model which takes into consideration both these factors in predicting number of faults removed from software.
Prashant Johri, Md. Nasar and Udayan Chanda [36]	Genetic Algorithm	Distribute total testing resources optimally under dynamic condition using optimal control theory and genetic algorithm.
Md Nasar, prashant johri and Udayan chanda [37]	Differential Evolution	Distribute total testing resources optimally under dynamic condition.
Y.S. Dai et.al [41]	Multi   objective   Genetic Algorithm	Author presented a genetic algorithm for testingresource allocation problems that can be used when the software systems structure is complex, and also when there are multiple objectives. Author used GO model for developing the model.

• IV.    Conclusions

In this paper, we have reviewed the cost optimization problem and release time in detail. The main contribution of the research presented is to demonstrate the important fact in the optimal software release problem, optimization problem in software reliability and type of optimization problem. Further, we have surveyed the software release policies based on the dual constraints of cost and reliability for SRGMs. Summary of important findings is also discussed in tabular form.

• V.    Future scope

Although there has been ample research on various facets of Resource allocation and Release time, but still some areas have to be addressed extensively. From the review some models are given, based on the assumption that at any point of time the total resources allocated for debugging and testing is fixed. For overcome this issue fuzzy logic and Neuro -Fuzzy, Genetic Algorithm and other soft computing techniques can be use for dynamically allocation of testing resource. Dynamic optimization is a process of finding the optimal control profile of one or more control variables or control parameters of a system. Optimality is described as the minimization or maximization of an objective function without violating given constraints. soft computing techniques (Genetic Algorithms, Differential Evolution etc.) for optimally allocate the resources for testing and debugging purpose so that cost of software during testing and operational phase will be minimized. Genetic Algorithms (GA) stand up a powerful tool for solving search and optimization problems. GA always considers a population of solutions that offers a lot of advantages. GA has been used to solve many difficult engineering problems and is particularly effective for combinatorial optimization problems with large, complex search spaces [38]. The GA has been applied to the reliability allocation problem of a typical pressurized water reactor in nuclear power plants in [39] and has also been used in system reliability by [40].