Согласованное многоканальное разделение сигнала: фильтрация и мультиплексирование

Система согласованного многоканального разделения (СМР)1) служит для выделения и передачи по нескольким каналам компонент сигнала в отдельных его частотных диапазонах с пониженной эффективной частотой дискретизации. Такая система за счет разделения общей частотной полосы сигнала на диапазоны обеспечивает снижение межсимвольной интерференции, позволяет осуществлять рациональные формы кодирования сигналов и изображений, а также скремблирование речевого сигнала с целью повышения степени конфиденциальности передаваемой информации. Аналогичным образом могут решаться и другие задачи преобразования спектрального состава сигнала. Некоторые виды систем согласованного многоканального разделения сигнала нашли отражение в работах Крочиере, Вебера и Фланагана (Crochiere, Webber, Flanagan) [1], Чу (P. Chu) [2], Галанда и Нусбаумера (Galland, Nussbaumer) [4], Ветерли и Хирли (Vitterley, Herley) [4], Herley [5], Смита и Эдинса (Smith, Eddins) [6], Эроувуда и Смита (Errowood, Smith) [7], Вайдианатана (Vaid-yanathan) [8]. Методом СМР рассматривались различные структуры, например структура, использующая так называемые квадратичные зеркальные фильтры, где "полу-полосным" фильтрам (ФНЧ и ФВЧ) с невысоким качеством предшествует прореживание отсчетов с N = 2, а различные фильтры, входящие в структуру, выводятся из одного прототипа [2], [3].

Система согласованного многоканального разделения (СМР) сигнала включает набор фильтров анализа (НФА), набор фильтров синтеза (НФС) и устройства кодирования или скремблирования для каждой из компонент сигнала, выделенных в отдельные каналы системы СМР. После каждого фильтра анализа специальное устройство производит снижение эффективной частоты дискретизации (ЭЧД), а перед каждым фильтром синтеза производится восстановление первоначальной частоты дискретизации. Таким образом, согласованный набор фильтров анализа производит несколько выходных сигналов после фильтрации и кратного снижения числа (скорости) отсчетов исходного сигнала. На приемном конце СМР у компонент восстанавливается исходная частота дискретизации, после чего через фильтры синтеза (НФС) они суммируются и образуют выходной сигнал с новыми характеристиками.

Главной особенностью системы согласованного многоканального разделения является возможность полного (без искажений) восстановления сигнала на выходе СМР и то, что это достигается при отсутствии сколько-нибудь жестких требований к качеству фильтров в НФА и НФС. Это свойство систем СМР реализуется за счет самой структуры согласованной фильтрации компонент сигнала и достигается за счет снижения ЭЧД в каналах связи НФА и НФС. Наиболее отчетливо свойство проявляется при многоканальной передаче больших потоков информации, которая реализуется для снижения межсимвольной интерференции. Свойство полного восстановления сигнала (после его декомпозиции) без частотных искажений (так называемого элайзинга, связанного с явлением Гиббса) играет основную роль как при решении задач кодирования сигналов и изображений или скремблирования, так и при различных других формах преобразования спектра сигнала.

СТРУКТУРА СИСТЕМЫ МНОГОКАНАЛЬНОГО РАЗДЕЛЕНИЯ

Концепция систем СМР и развитие элементов их теории связаны с работами Вайдианатхана (P.P. Vaidyanathan) [8–10]. Им доказано отсутствие межканального просачивания частот (так называемого элайзинга) и возможность вполне корректного (без искажений) восстановления сигнала на выходе единой системы НФА и НФС.

Система СМР представляет функциональное устройство, схемотехнически производящее М сигналов из единого входного сигнала посредством фильтрации М согласованными фильтрами. Полученные компоненты-сигналы имеют более низкую эффективную частоту отсчетов. Это достигается введением (в каждом канале) специальной процедуры N -кратного прореживания отсчетов сигнала — эта процедура сохраняет только каждый N -й отсчет.

При восстановлении сигнала (с помощью дуальной процедуры) из компонент, полученных в системе СМР на выходе НФА, производится обратное повышение скорости отсчетов с помощью так называемого "интерполирования", при котором между каждой парой ранее прореженных отсчетов вставляется N– 1 нулей. Интерполированные компоненты сигнала поступают на фильтры синтеза НФС, после чего они суммируются и образуют сигнал выхода СРМ.

В рамках анализируемого метода СМР отпадает необходимость применения правил Котельникова—Шеннона для выбора частоты временнóй дискретизации сигнала в отдельных каналах системы анализ—преобразование—синтез. Снимается также потребность в высококачественных полосовых фильтрах, т. к. теоретическая основа метода СМР позволяет рассматривать НФА и НФС как совокупность каналов в целом, а не отдельные каналы. Одной из наиболее значимых особенностей системы СМР является одновременность обработки сигнала и то, что различные фильтры, входящие в ее структуру, выводятся из одного прототипа.

Наименее сложными формами являются структуры с однородной системой фильтров на основе полифазного выполнения или на основе функциональных блоков преобразования Фурье (ПФ). Такие структуры систем СМР применяются в приложениях, использующих мультиплексирование на основе частотного или временнóго разделения канала, а также при спектральном анализе нестационарных сигналов. В современных беспроводных линиях и сетях связи эти виды мультиплексирования называют уплотнением с временным разделением и уплотнением с частотным разделением 2).

Системы СМР при их реализации в форме сопряженных наборов фильтров (НФА и НФС) относятся к классу систем, периодически изменяющихся со временем, у которых производится смена эффективной частоты дискретизации (ЭЧД) сигнала в сторону снижения и затем повышения. Поэтому анализ систем СМР целесообразно начать с рассмотрения функциональных элементов, реализующих прореживание сигнала и повышение его ЭЧД до исходного уровня.

ОСНОВНЫЕ ОПЕРАЦИИ В СИСТЕМАХ МНОГОКАНАЛЬНОГО РАЗДЕЛЕНИЯ СИГНАЛА

Основными операциями СМР являются линейная фильтрация, снижение ЭЧД сигнала путем прореживания его отсчетов и увеличение ЭЧД до начальной величины путем "интерполирования" посредством заполнения промежуточных отсчетов нулями. Статус СМР как линейной системы с периодическим изменением во времени определяется наличием функциональных элементов, выполняющих именно эти две операции, и период такой системы равен N .

Параметрами системы СМР, существенно влияющими на ее структуру, является число каналов М и коэффициент N прореживания отсчетов сигнала. Фактически с коэффициентом N снижается ЭЧД сигнала в каждом из каналов, а затем с тем же коэффициентом осуществляется обратное восстановление ЭЧД в наборе фильтров синтеза методом интерполирования. Такая система может моделироваться N передаточными функциями, соответствующими отклику системы на импульсное воздействие в моменты времени 0, 1, ..., N– 1. Если считать, что известны z -преобразования этих передаточных функций и они имеют вид T 0 ( z ), ..., T N– 1 ( z ), то в векторной форме они представляются как t ( z ) = [ T 0 ( z ), T 1 ( z ), ..., T N –1 ( z )]^T. ³⁾

Для получения компактной формы аналитического описания системы СМР и общих структур на базе НФА и НФС удобно ввести так называе- мое полифазное разложение (размера N) входного сигнала s(t) для области z-преобразования S(z). Это разложение группирует все отсчеты входного сигнала, имеющие одинаковую фазу (по модулю N, где N — период системы СМР), и может быть записано в форме вектора

S _n ( z ) = [ S п о ( z ), S _ti( z ), K , S п n -i ( z )] ^T , (1)

где S п i (z) = zi P z - kN • s (kN+i) — i-компонента k=-& полифазного разложения (ПФР) сигнала в области z-преобразования 4); п — индекс, указывающий на полифазность представления.

Используя приведенное выше обозначение вектора передаточных функций t ( z ) (в z -области), можно представить преобразование сигнала на выходе линейной периодической системы (пока без прореживания отсчетов) в виде выражения:

S b_HX.( z ) = [ t ( z )] ^T • S _n ( z ). (2)

Возможен и другой подход к представлению преобразования сигнала в линейной периодической системе. Этот подход основан на методе дискретного преобразования Фурье и его отражении в z -области. Используется входной сигнал s ( t ) (с N отсчетами), z -преобразование которого умножается последовательно на возрастающие степени ("модулирующего") множителя W = exp( - j 2 п / N ). Таким способом образуется N -мерный вектор-сигнал в z- области, называемый разложением с модуляцией (РМ):

S _M ( z ) = [ S ( z ), S ( Wz ),..., S ( W N ^{- 1} z )] ^T , (3) где W = exp( - j 2 п / N ); S(W^kz )— k -я компонента разложения; м — индекс, указывающий на РМ.

Полифазное представление сигнала и его представление на основе преобразования Фурье (ПФ) (представление в форме РМ) относятся к одному и тому же сигналу и построены для описания отдельных структур СМР, относящихся к классу линейных систем с периодическим изменением во времени. Поэтому оба типа представлений связаны друг с другом, и их соотношение можно компактно выразить, используя матричную форму дискретного ПФ.

• ■    Матрица F преобразования Фурье (размера N^N) имеет вид: F = [ F_ik ] , где F_ik = W ik [12].

• ■    Полифазное разложение и разложение с модуляцией сигнала для описания линейной периодической системы связаны соотношением

S _n ( z ) = N F • S m ( z ).                (4)

Использование (2) и (4) позволяет представить выходной сигнал в линейной и периодической системе выражением (5):

S вых. ( z ) = -[ t ( z )] ^T • F • S m ( z ).       (5)

Это выражение, альтернативное к (2), определяет выходной сигнал (в z -области) в виде линейной комбинации фильтрованного набора z -образа входного сигнала { S ( z ), S(Wz ),..., S(W N ^{- 1} z )}.

Представления способом разложения с модуляцией (с матрицей ПФ) и полифазное являются основными методами в анализе линейных и периодически изменяющихся со временем систем. По аналогии с анализом обычных систем первый способ (на основе ПФ) можно рассматривать как частотный подход к трактовке системы, а второй (с ПФР) — как временной подход. При этом, как показывают (2), (4) и (5), оба подхода в определенной степени равнозначны, и элементом их связи служит матрица ПФ. Дальнейшее применение одной из этих двух форм представления линейных и периодически изменяющихся со временем систем будет определяться тем, какая из них наиболее удобна при анализе определенной ситуации.

Как отмечено выше, основными операциями, которые реализуются структурными элементами системы СМР, являются: прореживание отсчетов входного сигнала; восстановление исходной ЭЧД интерполированием, состоящим в заполнении нулевыми значениями недостающих отсчетов между прореженными отсчетами,⁵ ) и фильтрация.

Если сигнал s ( n ) с z -преобразованием S ( z ) прореживается с коэффициентом N , то (как показывает правило использования ПФ) z -образ результирующего сигнала S _вых . ( z ) имеет вид

• 1    N -1

S вы., ( z ) = -Г s ( W k z“ ^N ).         (6)

N k = 0

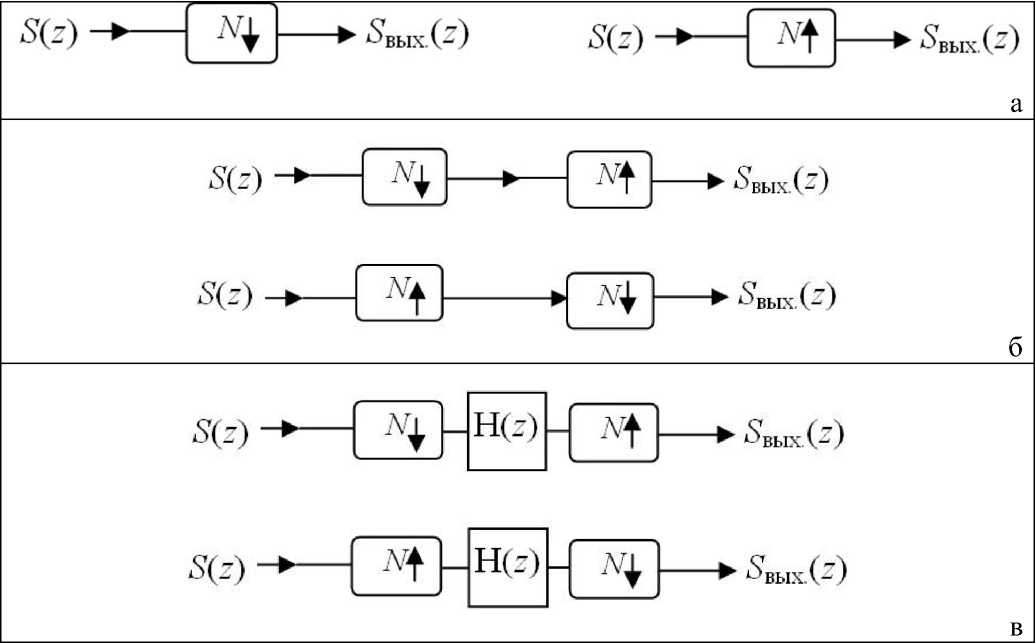
Рис. 1. Функционные элементы структуры систем сигналов. а — прореживание

N Ф и интерполяция

СМР, выполняющие основные операции преобразования N Т ; б — прореживание с последующей интерполяцией и интерполяция с последующим прореживанием; в — (прореживание, H(z)-фильтрация, интерполяция) и (интерполяция, H(z)-фильтрация, прореживание)

Соотношение (6) при использовании (1)-(4) может быть представлено в векторной форме выражением (7) 6)

х „. ( z ) = N [ 11...1 J - S - ( z" ) =

^N N                 (7)

= [ 10...0 ]. S _n ( z^1N ).

NN

Если сигнал 5 _вых . ( n ) получен путем интерполирования с коэффициентом N из сигнала 5 ( n ), то z- преобразования этих двух сигналов связаны соотношением (8):

X вых. ( z ) = X ( z^N ).                        (8)

Операции, соответствующие выражениям (6) и (8) и используемые в последующем анализе струк-

• ⁶⁾    В формуле (7) и далее под строкой указывается размерность соответствующего вектора или матрицы; в (7) это размерность N векторов [11...1], [10...0] и 8 _п ( z"^N ) .

тур систем СМР, показаны на рис. 1. В табл. 1 даны соотношения входа и выхода (в области z -преобразования) при поступлении сигнала на один из структурных элементов СМР или при прохождении сигнала через два таких (последовательно связанных) элемента.

ОСНОВНЫЕ СТРУКТУРЫ СИСТЕМ СМР-СИГНАЛОВ

Наиболее часто используемая структура согласованного многоканального разделения сигналов состоит из двух наборов фильтров — анализа (НФА) и набора фильтров синтеза (НФС). Таким образом, в системе СМР выполняются два этапа, для которых служат соответственно две различные конфигурации: НФА реализует собственно функцию согласованного многоканального ( М -ка-нального) разделения сигнала с одновременной операцией прореживания; НФС осуществляет восстановление единого (возможно, преобразованного) сигнала из его компонент в М каналах.

Табл. 1. Основные операции структурных элементов системы СМР и соотношения входного и выходного сигналов (в z -области) при соответствующем преобразовании

№ п/п	Вид операции или последовательно выполняемой группы операций	Соотношение входного и выходного сигналов (в области z -преобразования)
1	Прореживание N Ф	S в„. ( z ) = -1 N Z S ( W k z”N ) N k =0
2	Интерполирование N Т	S _( z ) = S ( zN )
3	Прореживание N Ф с последующим интерполированием N Т	S вых. ( z ) = -1 Z S (W-z ) N к = 0
4	То же, что 3, но с промежуточной фильтрацией H( z )	S b„ . ( z ) = J:H( z N ) N - ; S (W k z ) N        к = 0
5	Интерполирование N Т с последующим прореживанием N Ф	S вых. ( z ) = S ( z )
6	То же, что 5, но с промежуточной фильтрацией H( z )	S вых. ( z ) = J- S ( z ^ Z HtW k z1 N ) N      к = 0

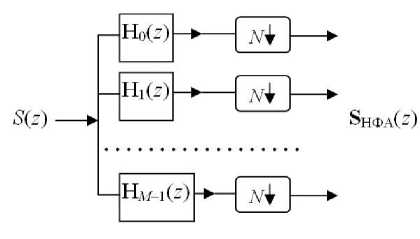
а

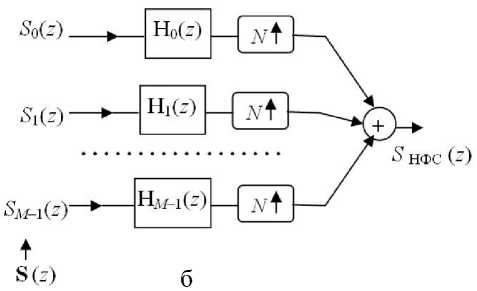
Рис. 2. Структуры основных функциональных компонент СМР: а — НФА; б — НФС

Конфигурация НФА с М каналами и коэффициентом прореживания N определяется М -вектором фильтрации H ( z ), компонентами которого являются импульсные передаточные функции (в z -области) H₀( z ), H i ( z ), ..., H M _ф z ) (рис. 2, а). М -вектор сигнала после фильтра S _вых .ф. ( z ) определяется соотношением

S b_Mx^,( z ) = H ( z ) • S ( z ). (9)

М -вектор выхода НФА после прореживания отсчетов S _{вых нфа} ( z ) может быть представлен (с помощью (6) и (9)) выражением (10):

S

M

N - 1

НФА ( z ) =   Z S вых^^" N ) =

N к = 0

M

N —1

= — ^H (W k z^1Z N ) • S (W k z^{1Z N} ).      (10)

N k=0

M

Подобно тому, как это было сделано в (7), выражение (10) удобно представить в векторноматричной форме. Для этого вводится ( N х N)- матрица H M ( z ) передаточных функций для М каналов (в z -области), основанная на ПФ и называемая также матрицей модулированных фильтров:

H м = [ H ( z ), H ( Wz ),..., H ( W N ^{— 1} z )] =

H_o( z )     H 0 ( Wz )   ...   H 0 ( W N ^{— 1} z ) ■

H₁( z )     H₁( Wz )   ...    H₁( W N ^{— 1} z )

...                           ...                  ...                       ...

. H M — 1 ( z )  H M — 1 (Wz )  ...  H M — 1 (W^{N — 1} z )

При этом (с учетом (3) и (11)) выражение (10) приобретает компактную форму в виде соотношения (12):

£

НФА

M

( z ) = N • H M ( z^1N ) • S M ( z^1N ).

M x N

N

Аналогичное представление сигнала на выходе НФА может быть получено через полифазное разложение сигнала, поступающего в систему СМР (т. е. через S _n ( z )). Для этого достаточно подставить в (12) величину S _m ( z ), которая получается с помощью обращения выражения (4). Это непосредственно дает соотношение (13)

S _H ФА ( z ) = H M ( z^1N ) ■ F ^{- 1} - S _n ( z^1N ),      (13)

где F ^{- 1} — матрица, обратная относительно матрицы F дискретного ПФ.

Представление сигнала на выходе НФА через полифазное разложение входного сигнала может быть также выражено в компактной форме после использования двух небольших преобразований. Эти преобразования включают следующее.

— Применение обозначения для полифазной матрицы передаточных функций М каналов системы СМР (определения, которое по форме аналогично (11)):

Hn(z) = 1-Hм(z)• F .(14)

N

M x NM

— Выражение обратной матрицы ПФ F ¹ через прямую матрицу F и матрицу перестановок J 7) :

F -1 = ' • F • J ,(15)

Nx N    N N xN N xN где матрица J имеет вид

" 1     0    0    0    ...0

0    0    0    ...    01

0    0    0    ...    10

J =

0 K K K K

0   0   1    0

0    1     0    0    ...0

С использованием (14) и (15) сигнал на выходе НФА выражается через полифазное представление входного сигнала соотношением (16):

SHФА (z) = Hn (z1N) ■ J-Sn (z1N).(16)

• ⁷⁾    Матрица J изменяет номер i у каждой строки (или столбца) на номер N - i ( i = 0, 1,..., N- 1).

Конфигурация НФС с М каналами и коэффициентом интерполирования N рассматривается здесь сначала независимо от НФА (принимая в качестве входного сигнала просто вектор-сигнал S ( z )). После выполнения преобразований, связанных с получением общей формы передаточной характеристики НФС (как некоторой самостоятельной подсистемы), будет проанализирована системы СМР в целом и виды ее структурных вариантов (в этом случае входным сигналом для НФС будет выходной М -вектор-сигнал с выходов НФА).

Выход НФС S _НФС ( z ) (как автономной подсистемы с входным М -вектором S ( z ) и с импульсной передаточной функцией в виде М -вектора H ( z )) определяется (в области z -преобразования) соотношением (17) (рис. 2, б):

S НФС ( z ) = [ H ( z )]^T • S ( z ^N ).                (17)

M x1            M x1

Так получено полное представление в z -области вида преобразований сигнала набором фильтров анализа и набором фильтров синтеза, которые входят как составные части системы согласованного многоканального разделения сигнала. Представление для НФА выражается соотношениями (10)-(12) через модулированное разложение входного сигнала и соотношениями (13)(16) — через его полифазное разложение.

ПРИМЕНЕНИЕ СИСТЕМЫ СМР ДЛЯ ПОСТРОЕНИЯ СУБПОЛОСНЫХ КОДЕРОВ И МУЛЬТИПЛЕКСИРОВАНИЯ

В модификациях структуры систем СМР восстановление сигнала может быть реализовано как на выходе НФС, так на выходе НФА. Первую модификацию, в которой за НФА следует НФС и объединение выходов НФС обеспечивает восстановление сигнала, относят к субполосным кодерам. Это является одним из наиболее широко используемых приложений таких СМР [1, 6] . Типовая конфигурация кодера показана на рис. 3, где блоками C₀( z ), C 1 ( z ), .„, C _M- 1 ( z ) представлены фильтры-преобразователи, осуществляющие субполосное кодирование сигнала.

Промежуточные блоки {C k } _k =₀,₁,_M _- 1 могут выполнять различные формы скремблирования: частотную инверсию (ЧИ), ЧИ с тональным маскированием и с использованием ПФ. Одна из наиболее совершенных форм основана на применении вейв-лет-преобразования (ВП) со скремблированием коэффициентов ВП и последующим применением преобразования Адамара [12] .

Вторую модификация системы СМР, в которой НФС предшествует НФА, относят к системам мультиплексирования — уплотнения канала связи

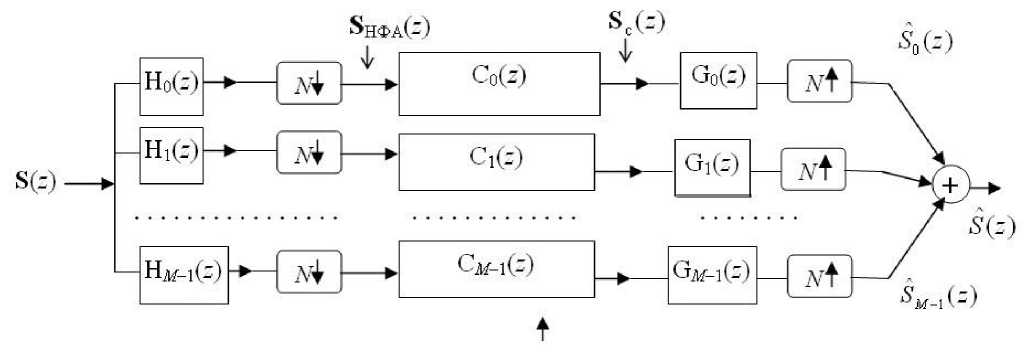
Рис. 3. Субполосный кодер с М каналами и коэфициентом прореживания N . Блоки С k ( k = 0, 1,…, M –1) — "фильтры-преобразователи" кодирования, например скремблирования; блоки G k — набор фильтров синтеза

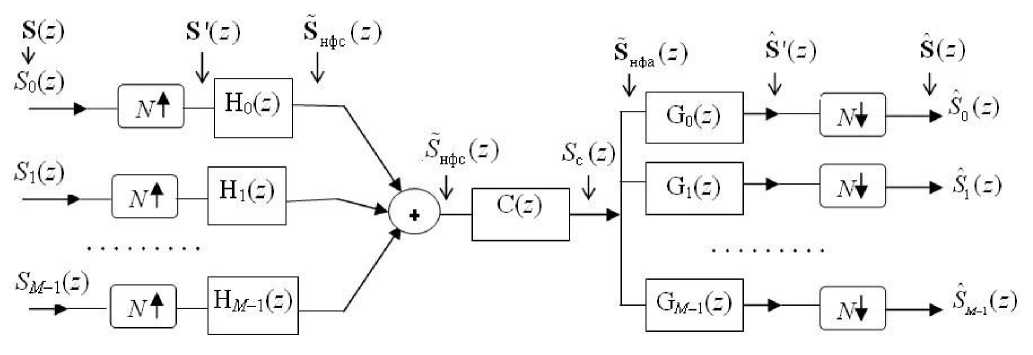
Рис. 4. Мультиплексирование М каналов с коэффициентом N повышения частоты (и таким же коэффициентом прореживания). Блок C( z ) осуществляет промежуточное преобразование

с временным или частотным разделениями. Такая система состоит из двух основных функциональных блоков — собственно мультиплексора и демультиплексора. Мультиплексор, являющийся фактически НФС, объединяет (уплотняет) данные из М входных линий (повышая их ЭЧД при частотном разделении) и передает их по каналу связи высокой емкости. Демультиплексор (после возможного промежуточного преобразования, включая кодирование) принимает уплотненный поток данных, распределяет (разуплотняет) данные по информационным каналам и доставляет их на соответствующие выходные каналы (рис. 4). При этом частотное разделение осуществляется, когда частотная полоса канала значительно превосходит частотный диапазон сигналов, а временнóе — ко- гда скорость передачи по каналу связи превосходит скорость поступления информации по каждому из М каналов.

ФОРМА ОПИСАНИЯ ДВУХ ОСНОВНЫХ СТРУКТУР СМР, ПОСТРОЕННЫХ НА ОСНОВЕ НФА И НФС

Выбор параметров и характеристик, соответствующих конкретным условиям применения систем СМР для субполосного кодирования или уплотнения канала связи (мультиплексирования) с временным или частотным разделением, может наиболее эффективно производиться на основе достаточно полного представления о формальном опи- сании таких систем. В связи с этим мы проанализируем этапы преобразования сигналов в отдельных элементах структуры двух основных модификаций систем СМР.

Система СМР для субполосного кодирования

Как уже отмечалось, в системе субполосного кодирования НФА предшествует НФС. Выход НФА поступает в фильтры C i ( z ) — преобразователи кодирования (скремблеры) и затем поступает на НФС, выход которого является восстановленным (в едином канале) сигналом, несущим запланированную форму кодирования.

Поскольку выход НФА по (12) определяется соотношением S нфА ( z ) = N H м ( z 1 N ) • S м ( z 1 N ), то после преобразователей кодирования сигналы в каналах имеют вид:

C z ) = C ( z ) • S нфА .

MxM

Здесь C ( z ) — диагональная ( М*М )-матрица передаточных функций набора фильтров-преобразователей субполосного кодера, которая в развернутом виде определяется выражением (19):

C ( z ) =

Co( z )	0       ..	..           0
0	C 1 ( z )   ..	..           0
0	0       ..	..           0
0	0       ..	с '. C M -1

Для описания НФС служит полученное выше соотношение (17). Использование в нем выражений (12) и (17) позволяет получить представление выходного сигнала S(z) системы субполосного кодирования в виде:

S ( z ) = N [ G ( z ) ] • C ( z^N ) • H M ( z ) • S M ( z ),      (20)

где G ( z ) — вектор набора фильтров синтеза.

Это соотношение может быть представлено также с полифазной формой S _м ( z ) разложения исходного сигнала. В этом случае использование (4) и (14) позволяет преобразовать (20) к соотношению (21):

S ( z ) = N [ G ( z ) ] • C ( z^N ) • H _n ( z ) • J • S _n ( z ).    (21)

На основе выражений (20) и (21) можно установить основные свойства системы СМР для субполосного кодирования по схеме, представленной на рис. 3 (где фильтры-преобразователи кодирова- ния предполагаются независимыми от времени).

• ■    Сигнал на выходе субполосного кодера получается без межканальных частотных искажений (без так называемого эффекта элайзинга) при условии выполнения соотношения

[ G ( z ) ] ^T • C ( z^N ) • H м ( z ) =

1x M       M x M      M x N

= [ F ( z ) 0       0       ...       0 ] .       (22)

где F ( z )— передаточная функция (в z -области) какого-либо фильтра-преобразователя.

• ■    Вполне корректное восстановление сигнала на выходе субполосного кодера обеспечивается также при выполнении условия, определяемого соотношением:

[ G ( z ) ] ^T • C ( z^N ) • H m ( z ) =

= [ z -1 0     0     ...     0],                (23)

1x N где z-1 указывает на элементарную задержку (соответствующую интервалу используемой временной дискретизации).

Система СМР для уплотнения каналов (мультиплексирования)

В системе СМР с временным и частотным уплотнениями, конфигурация которой приведена на рис. 4, повышение ЭЧД описанным выше методом интерполирования производится для входного сигнала, а прореживание (поканально с коэффициентом N ) осуществляется на выходе системы мультиплексирования. Канал представлен (линейным) фильтром-преобразователем C( z ). Сигнал S _НФC ( z ) , поступающий в канал, определяется выражением (17) (на рис. 4 он отмечен как S _нфс( z ) ), а значение S C сигнала на выходе из канала описывается выражением (24) ⁸⁾:

Sс = C( z) • S*фс( z) = C( z) • [H( z )]T • S(zN).(24)

1 x M

Поэтому с учетом (12) вектор-сигнал S на выходе уплотнителя канала определяется соотношением

S (zN) = N G • Sc( z),(25)

где S _C ( z ) по (24) равно выражению

5 _с ( z ) = C( z ) • [ Щ z ) ] ^T • S ( Z N ).

Объединение последнего выражения и (25) приводит вектор-сигнал S на выходе уплотнителя канала к виду

S ( z^N ) = N G • C( z ) • [ H ( z ) ] • S ( z^N ).      (26)

ДРУГИЕ ПРИМЕНЕНИЯ СИСТЕМЫ СМР

Общая концепция построения и использования систем СМР обеспечивает определенную степень структурной и функциональной гибкости. На основе этой концепции возможно построение различных систем СМР для решения ряда прикладных задач. Одной из таких задач является реализация вращаемого преобразования Фурье (ВПФ) [13]. Другая задача связана со снижением уровня шума для нестационарных сигналов, у которых информационная компонента может прерываться микропаузами, которые несут только фоновую составляющую общего зашумленного сигнала.

M -точечное ВПФ

Получение М- точечного ВПФ { S^a ( m ) m = ₀ , ₁₁₂ ,_, _M- 1 } от последовательности { s ( n )} M^- отсчетов сигнала включает ряд этапов. Выражение s^a ( m ) представляется с помощью ядра ВПФ. В векторноматричной форме это представление имеет вид:

sa = Ka s, 0 < а < 2п , где sa = (sa (0),sa (1),...,sa (M -1))T ;

s = ( s (0), s (1),..., s ( M - 1)) ^T .

Матрица ("ядро") дискретного а -ВПФ используется в так называемой полифазной форме, в которой ее элемент [ K _a ] mn выражается соотношением (27):

^{[ К} а ^] mn = K a ⁽ m , n ) = a 0^{( a} ) ' ^{5 [(} m ^- n ) M ^{] +}

+a 2(a) • 5 [(m + n) m ] + a1(a)

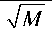
exp ( - 2 п jmn / M )

+ a 3^{( a} ) M

exp ( 2 п jmn / M ) ,

где a0(a) = 0.5(1 + eja) cos a; a1(a) = 0.5(1 - eja )sin a;

a ₂( a ) = 0.5( - 1 + e^{j a} )cos a ;

a₃( a ) = 0.5( - 1 - e^{j a} )sin a ;

5 [( m - n ) _M ] и 5 [( m + n ) _M ] — обычные символы Кронекера, их значение равно единице только при условии, что аргумент (в квадратных скобках) равен нулю по модулю М .

Для М -периодической последовательности { s ( n ) M } отсчетов сигнала оператором обращения времени служит ( W )², где W — матрица оператора дискретного преобразования Фурье, которая имеет элементы

W_nk = (1/V N ) • exp( - 2 п jnk / N ), 0 <  k , n <  N - 1.

Поэтому оператор ВПФ (с параметром а ) из (27) представляется в виде

K _a s = a ₀( a ) • s ( n ) + a ₂( a ) • s ( - n ) +

+ a 1 ( a ) • S ( n ) + a ₃(a ) • 5 ( - n ),             (28)

и, следовательно, дискретная форма ВПФ s ( n ) выражается в виде линейной комбинации величин s ( n ), s (- n ) и соответствующих им ПФ сигнала — S ( n ) и S (- n ). Таким образом, с использованием подходящей структуры (рис. 5) дискретное ВПФ с угловым параметром а ( а -ДВПФ) может быть достаточно эффективно вычислено с применением известного метода быстрого преобразования Фурье (БПФ) [14].

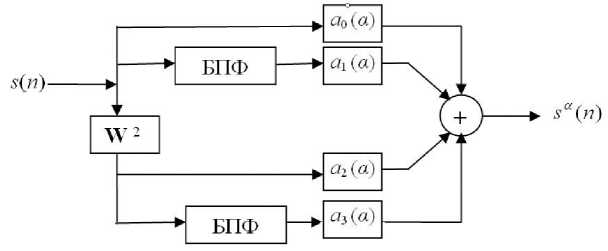
Рис. 5. Способ непосредственного получения дискретного вращаемого преобразования Фурье ( а -ДВПФ) с использованием БПФ

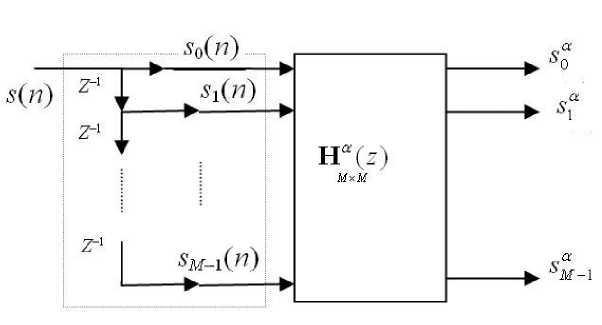
Рис. 6. Способ прямого выполнения дискретного вращаемого преобразования Фурье ( а -ДВПФ) с элементами структуры СМР

Прямое выполнение ДВПФ на основе системы СМР может быть осуществлено и без использования БПФ. Для этого достаточно из М отсчетов { s ( n )} M^— (на каждом периоде) периодического сигнала s ( t ) с помощью элементов задержки ( z ^-1) создать параллельный поток (рис. 6). При этом отсчетам s ( n ) исходного сигнала будет соответствовать М -вектор ( s ₀( n ), s i ( n ), ..., s_M- i ( n ))^T, где s i ( n ) = = s ( n - i ). Приведенная выше векторно-матричная форма а -ВПФ в развернутом представлении имеет вид s m ^{( n} ) =Ё ' V s i ^{( n} ) K a ⁽ m , i ).

С учетом наших обозначений и того, что s i ( n ) = = s ( n-i ) является задержкой исходного сигнала на i единиц (дискретного времени), это выражение в области z -преобразования представляется в форме (29):

M - 1                    M - 1

S m ( z ) = Ё S i ( z ) K a ( m , i ) = Ё K a ( m , i ) z'S ( z ). (29) i = 0                               i = 0

Соотношению (29) можно придать более компактный вид

M - 1

s k ( z ) = H k ( z ) S ( z ), где H k ( z ) = £ K a ( m , i ) * z (30) i = 0

который и используется в структуре системы СМР для прямого выполнения а -ДВПФ (рис. 6).

Из общих свойств оператора М -точечного дискретного ВПФ (с угловым параметром а ) полезно отметить его периодичность по времени и по частоте:       K _a ( n , k ) = K _a ( n + M , k ) = K _a ( n , k + M ) =

= K _a ( n + M , k + M ). Так что а -ДВПФ периодического сигнала само является периодическим.

Снижение уровня шума нестационарного сигнала

Важной областью приложения систем СМР является использование неоднородной полифазной структуры для снижения уровня шума нестацио- нарного сигнала, имеющего (случайно распределенные) микропаузы с отсутствием информационной компоненты. Метод, который оказывается эффективным в ситуации такого типа, целесообразно проанализировать на задаче улучшения речевого сигнала (РС) на основе так называемого спектрального вычитания [15]. РС является (практически) немоделируемым нестационарным сигналом со спорадически возникающими естественными микропаузами, и по этому свойству он подобен многим разновидностям сигналов в информационных системах (ИС) 9), в которых источник возбуждения контролируемого сигнала не действует непрерывно, так что при этом возникают микроинтервалы, несущие только шумовую компоненту измерительного тракта ИС.

В методе спектрального вычитания из общего спектра зашумленного РС вычитается текущая оценка среднего спектра шума, причем процедура обычно выполняется в области ДПФ или вейвлет-преобразования. Более совершенная форма такого анализа РС может быть основана на системе СМР с однородными (по ширине) полосами или с логарифмически однородными полосами у НФА, которые лучше приспособлены к так называемой персептуальной модели, отражающей особенности восприятия звуковой информации органами слуха человека.

ЗАКЛЮЧЕНИЕ

Проанализированы методы обработки сигналов на основе специальной структуры, называемой системой согласованного многоканального разделения (СМР).

• ■    СМР — это метод, обеспечивающий преобразование сигнала в группу (канально разделенных) сигналов существенно меньшей частоты. Полученные частотные компоненты могут использоваться при фильтрации, при кодировании речевого сигнала, для мультиплексирования и непосредственно в сетях коммуникации, где многоканальная передача снижает вероятность ошибок межсимвольной интерференции.

• ■    СМР включают набор фильтров анализа (НФА), набор фильтров синтеза (НФС) и, возможно, систему промежуточного преобразования — субполосного кодирования, скремблирования сигнала или изображения. Так что сигнал на выходе СМР может приобретать новые желательные свойства и при необходимости — может изменять свою частотную структуру.

• ■    Описание структуры СМР приведено в аналитической форме на основе ее представления в виде линейной периодической системы. Использованы два вида представления сигнала в СМР: 1) в виде полифазного разложения сигнала в области z -преобразования; 2) в виде разложения сигнала в z -области с модулирующим множителем на основе дискретного преобразования Фурье (ДПФ).

• ■    Полифазное представление сигнала и его представление на основе ДПФ использованы для описания структуры СМР.

• ■    Систематизирован характер изменения выходного сигнала (в z -области) после применения операций прореживания сигнала (уменьшения эффективной частоты дискретизации), интерполирования и фильтрации.

• ■    Приведены структуры основных компонент СМР, их объединение в системы СМР различного вида и использование систем СМР для субполосного кодирования сигналов и изображений, скремблирования сигнала (с целью обеспечения скрытой передачи информации) и мультиплексирования.

В последнее время все структуры СРМ находят применение:

― в области беспроводной связи: уплотнение канала с временным или частотным разделениями доступа;

― как средство получения обобщенной модификации преобразования Фурье (так называемой дискретной формы вращаемого преобразования Фурье);

― для снижения уровня шума нестационарного сигнала, имеющего микропаузы с отсутствием информационно значимой составляющей 10).