Согласованное многоканальное разделение сигнала с вейвлет-преобразованием и модифицированной полифазной структурой для спектрального вычитания фона речевого сигнала

Обычное спектральное вычитание фона (СВФ)1) с аналитической точки зрения сводится к введению спектральных весовых коэффициентов, видоизменяющих частотную форму (преобразование Фурье) зашумленного речевого сигнала (РС). Фактически метод реализует вычитание средней величины спектра шума из спектра РС и используется, когда искажение РС происходит за счет аддитивного шума с медленноменяющимися спектральными характеристиками. При этом выполняются прямое и обратное дискретное преобразование Фурье (ДПФ) в форме кратковременного ДПФ с частичным перекрытием "окна" преобразования. Более совершенным является метод СВФ, основанный на структурах согласованного многоканального разделения (СМР) сигнала [1, 2]. Для равномерной (по спектру) ширины каналов этот метод использовался Смитом, Эдинсом (Smith, Eddins) [3] и Аровудом (Arrowood), Смитом [4]. Метод СВФ с неравномерными по частоте каналами, приспособленными к персептуальной модели 2), которая отражает особенности восприятия звука человеком, использован в [6]. В этой работе СВФ реализовано на основе вейвлет-преобра-зования и предусмотрена адаптация к изменениям уровня и спектральной структуры фона. СВФ с использованием неравномерных каналов СМР и вейвлет-преобразования выполнено также Лангом, Гуо, Одегардом (Lang, Guo, Odegard) [7]. Однако процедура СВФ проведена только для семи каналов, а для коэффициентов вейвлет-преобразо-вания использована только простая "жесткая" пороговая дискриминация. Применение полужесткого порога для вейвлет-коэффициентов в сочетании с СМР было предложено Сеоком и Бае (Seok, Bae) [8].

В статье проанализированы две структуры согласованного многоканального разделения с неравномерной шириной каналов (ориентированных на персептуальную модель РС): структура с использованием дискретного вейвлет-преобразова-ния и полифазная структура [6], которая модифицирована за счет применения широкодиапазонных преобразователей вместо элементов задержки (обычно используемых в системах СМР) между входными сигналами отдельных каналов.

В этих структурах частотные диапазоны каналов организованы так, чтобы получить шкалу в барках (см. сноску 2)) и в области низких частот РС иметь возможность осуществлять более эффективное спектральное вычитание фона. Ширина шкалой частот в барках. Это разбиение в некоторой степени сходно с логарифмической шкалой, но не совпадает с ней.

полос в низкочастотной области РС (и количество каналов СМР в ней) выбраны таким способом, чтобы компоненты шума в интервале между гармоническими элементами сегментов РС могли быть взвешены по отдельности.

Кроме того, неточность воспроизведения РС на выходе структуры СМР должна быть мала с точки зрения субъективной оценки качества сигнала, переданного через систему СМР. Иначе говоря, РС, прошедший стадии анализа и синтеза в СМР без спектрального взвешивания, должен быть идентичен сигналу, поступившему на вход системы, т. е. по крайней мере не иметь слышимых искажений РС.

В связи с указанными требованиями к системе СМР полное восстановление РС не является безусловно необходимым, также как и прореживание частоты на входных цепях каналов СМР. Это позволяет при построении системы СМР найти рациональный баланс между допустимой ошибкой восстановления РС, частотным разрешением системы, достаточным для спектрального вычитания фона, и вычислительной сложностью алгоритма, который определяет совокупность операций, необходимых для реализации системы.

СПЕКТРАЛЬНОЕ ВЫЧИТАНИЕ ФОНА

При спектральном вычитании фона часто используется модель РС, загрязненного аддитивным гауссовым шумом: x ( k ) = s ( k ) + n ( k ), где x ( k ) — регистрируемый РС, s ( k ) — фактический РС, n ( k ) — шум, k — дискретное время отсчета сигналов. Частотный спектр РС со сниженным уровнем фона S ( e^{i ω} ) получаетс я вычи танием оценки средней величины фона | N ( e^{i ω} )| из величины спектра | X ( e^{i ω} )| регистрируемого РС ³⁾:

S ( e ™ ) = ( | X ( e™ I - | N ( e ™ | ) e x ⁽ ™ ) |, (1)

где ϕ _x ( ω ) — фаза регистрируемого РС; X ( e^{i ω} ), N ( e^{i ω} )и S ^ˆ( e^{i ω} ) — преобразования Фурье (ПФ) регистрируемого РС, шума и сигнала, полученного после спектрального вычита ния фона. Средняя величина спектра шума N ( e^{i ω} ) оценивается на интервалах естественных микропауз РС, которые могут детектироваться с помощью нейронной сети [9].

Таким образом, модифицируется только вели- чина X(eiω), а фаза сохраняется, какой была до операции спектрального вычитания (СВ). Этот метод СВ основан на том, что ухо человека относительно нечувствительно к возмущению фазы [10], а способ вычитания фазы пока не формализован.

Альтернативный способ оценивания среднего уровня спектра шума (без детектирования пауз) основан на слежении за минимумом сглаженной величины спектра зашумленного РС в некотором временнóм окне [11, 12]. Длина окна выбирается так, чтобы на нем присутствовали паузы РС. Соотношение (1) можно интерпретировать как спектральное взвешивание зашумленного РС:

S ( e i ) = G ( e i ) X ( e °™ ),              (2)

где

| X ( e ™ ) | -| N ( e ™ ) | | X ( e^{i ω} )|

Поэтому оценка спектра РС, свободного от шума, выполняется путем применения взвешивания, зависящего от спектра регистрируемого сигнала.

Получение в (3) отрицательного значения G ( e^{i ω} ) трактуется как ошибка оценки уровня фона. Для того чтобы такое G ( e^{i ω} ) не входило в схему СВ, вместо (3) используется соотношение (4) [13]:

G ( e ™ ) = max

| X ( e™ )| - | X ( e™ )| | X ( e^{i ω} )|

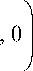
= max 1 -

| N ( e^{i ω} )| | X ( e^{i ω} )|

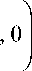
Для выполнения этого метода входной РС разделяется на мелкие сегменты по 10–50 мс, и применяется спектральное вычитание в пределах каждого сегмента. Чтобы не было артефактов СВ на границах сегментов, сегментация РС делается с набольшим перекрытием и так же осуществляется восстановление сигнала после процедуры СВ.

Методы СВ в описанной выше форме дают низкоуровневый остаточный шум РС, и для его подавления принимают дополнительные меры:

― частотный спектр входного сигнала может быть немного сглажен для снижения дисперсии компоненты шума;

― используется небольшая переоценка среднего спектра шума умножением его на число, несколько большее единицы, и этот коэффициент может видоизменяться вместе с уровнем шума;

― применяется порог для минимума оцененного спектра сигнала, так что оставшиеся спектральные пики маскируются даже небольшим уровнем широкополосного шума.

Общим для этих подходов к совершенствованию метода СВ является то, что при уменьшении уровня остаточного шума несколько возрастает искажение РС на выходе или становится меньшим снижение дополнительно возникающих шумов на стадии операций СВ.

Более сложная схема метода СВ предложена Капеланом, Страусом и Вари (Kapelan, Straus, Vary) [14]. Определяются апостериорное отношение сигнал/шум iϕ     |Xb(eiϕ)|2

апостер. b           _{| N (} e iϕ _)| 2

и априорное отношение сигнал/шум

R априор. b ( C i» ) = (1 — 9 ) • max ( R апостер. b ( C i» ),0 ) +

_{- 9} | G b -1 ( e i» ) • X b ( C » )I 2 | N b ( e^{i ϕ} )| ²

G_b _1 означает спектральные веса предыдущего сегмента РС, а b — индекс (номер) сегмента. Тогда спектральные веса текущего сегмента РС выражаются соотношением (7):

G b ( e » ) =X

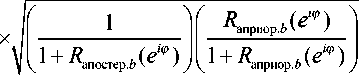
апостер.b iϕ Rаприор.b(e)

X

1 + R априор. b ( e » )

Функция M [ u ] определяется выражением

M [ u ] = exp

,

где функции I ₀ и I ₁ — модифицированные функции Бесселя первого и второго порядка.

НЕЛИНЕЙНЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ

Вейвлет-преобразование и структура СМР на его основе

Для спектрального анализа нестационарного процесса наиболее часто используется кратковременное преобразование Фурье (КПФ)

-to

F W ( t , to ) = J x ( t ) • w ( t - t ) e "^1ЮТ .        (9)

-to

Выбор (постоянной) длины окна этого преобразо- вания определяется приемлемым компромиссом между величиной разрешения по времени и по частоте, а так называемая "ячейка разрешения" 4) имеет одинаковый размер на всей время-частотной плоскости. Разрешение по частоте у КПФ оказывается одинаковым на всем частотном диапазоне спектра сигнала, и это основной недостаток КПФ.

Лучшими (сравнительно с КПФ) характеристиками разрешения обладает вейвлет-преобразование (ВП). Непрерывное ВП сигнала x ( t ) определяется с помощью единой функции ψ со смещением ее по времени и масштабированием ⁵⁾:

-to

W_x ^v ( b , a ) = | a Г¹/² f x ( t) w\ — \ d t •      (¹⁰)

-to to a )

Функция ψ служит прототипом вейвлет-базиса, который получается смещением времени и масштабированием с помощью параметров b и a . При больших значениях а базисные функции ^ ba ( t ) = 1 a I — ¹/² ^ ( ( t — b )/ a ) становится низкочастотными, при малых а ψ _{b , a} ( t ) — высокочастотные, и в разложении (10) они представляют соответствующую область спектра сигнала x ( t ). Разрешение во время-частотной плоскости не постоянное: в области высоких частот ВП имеет высокое разрешение по времени и небольшое по частоте; в области низких частот — высокое разрешение по частоте и небольшое разрешение по времени.

В частотной области ВП может интерпретироваться как СМР с полосовым пропусканием A to i , которое возрастает одновременно с возрастанием центральной частоты ω ₀ этой полосы. При этом величина относительной полосы Q = A to i /to ₀ не зависит от параметра а . В связи с этим использование ВП называют анализом с постоянной величиной относительной разрешающей способности (с постоянным качеством Q ). Для речевого сигнала такая форма анализа сходна со структурой частотного анализа, производимого слуховым аппаратом человека.

Избыточность ВП по непрерывным параметрам а и b снимается методом их дискретизации: a m = 2 m , b mn = a m nT , где m , n — целые, T — интервал дискретизации. При этом (10) приобретает форму (11), которая наиболее часто применяется в ВП:

-to

w : ( b mn , a m ) = | a r m ^/2 J x ( t ) : ( 2 ^- m t - nT ) d t . (11)

-to

Для повышения разрешающей способности по частоте ВП возможно использовать 1< а ₀< 2, однако при этом теряется бинарное свойство масштабирования базисных функций. Другой более эффективный способ повышения частотной разрешающей способности в М раз состоит в использовании

"расщепленной" функции ^ (прототипа базиса) в виде

: ^j ( t ) = 2 M : ( 2 M t ) , j = 0,..., m - 1.    (12)

Поскольку динамический спектральный анализ РС и других нестационарных сигналов производится с использованием их дискретной формы, для этих условий (11) принимает вид (13):

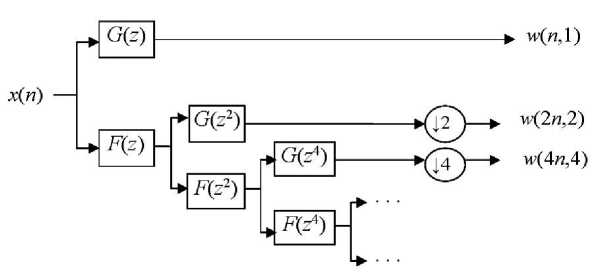
Рис. 1. Структура преобразований при реализации ВП по методу Малата— Шенсы

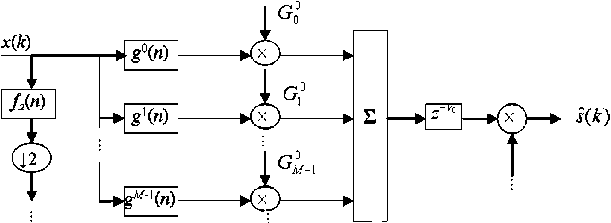
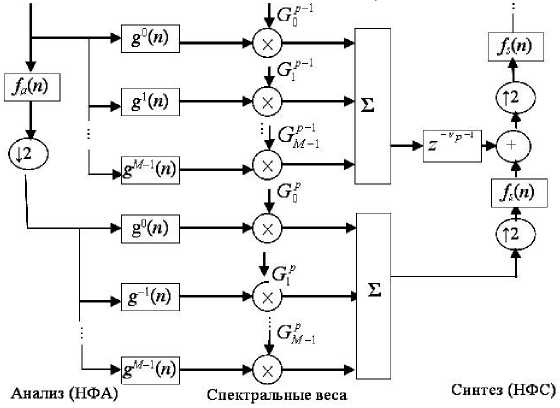
Рис. 2. Структура СМР для вейвлет-преобразования с высоким разрешением по частоте.

Элементы структуры СМР: НФА — набор фильтров анализа и НФС — набор фильтров синтеза описаны в [2] и [4].

С2^ и С!) — символы операций прореживания частоты и ее восстановления интерполированием

WV (2 m n ,2 m) = 2-m/2 Z x (k) • v (2-mk - n), (13) k где интервал дискретизации Т принят за единицу 6).

Структура преобразований для реализации ВП дискретного сигнала по (13) (т. е. при обычном разрешении по частоте) является своеобразной СМР. Один из видов структуры, отражающий метод Малата—Шенсы (Mallat, Shensa) [19], представлен на рис. 1, где G ( z ) — z -преобразование прототипа вейвлет-функции; F ( z ) — передаточная функция фильтра интерполяции.

Для получения более высокого разрешения по частоте методом расщепления прототипа базиса в соотношении (13) вместо функции ψ ( k ) следует использовать v j ( k ) = 2 ^- j ^/2 M v ( 2 ^- j ^/2 M k ) , j = 0, ..., M - 1 из соотношения (12). Поэтому для дискретного сигнала ВП с увеличенным в М раз разрешением по частоте должно использоваться выражение (14):

Wxj (2mn,2m) = 2-m/2 x xZx(k) • 2-j/2MV (2-j/M (2-mk - n)). (14) k

При анализе РС с повышенным разрешением по частоте свойство полного восстановления сигнала на выходе структуры СМР позволяет реализовать 2 ^m -кратное прореживание частоты в m -октаве более эффективно (сравнительно с непосредственным вычислением по соотношению (13)). Для этого может служить структура СМР на основе ВП. Эта вейвлет-структура СМР для ( p +1)-октавного спектрального разложения сигнала, дополненная М -кратным расщеплением функции ψ (прототипа базиса), представлена на рис. 2. Для анализируемого сигнала она обеспечивает М -кратное повышение разрешения по частоте.

Функция низкочастотного фильтра f a ( n ) состоит в снижении эффекта Гиббса — межканального просачивания частот (элайзинга). Прореживание частоты РС на 2 ^l в октаве l позволяет использовать в каждой октаве одинаковые фильтры. В цепях набора фильтров синтеза (НФС) восстанавливается частота в канале каждой октавы на выходе СМР, и сигнал суммируется с выходом следующей октавы НФС. При этом производится компенсация запаздывания сигнала в цепях НФА путем введения блоков задержки z - p ^{- 1}, z - p ^{- 2},..., z ^{- v 0}. Выполнение синтеза на выходе СМР не обеспечивает 100 %-го полного восстановления сигнала, но качество по-

лучаемого РС вполне достаточно с точки зрения персептуальной модели. Вместе с тем такая форма спектрального анализа с повышенным частотным разрешением имеет преимущество существенно меньшего объема вычислений (сравнительно с использованием общих аналитических соотношений).

Модифицированная структура СМР с полифазным преобразованием

Получение согласованного многоканального разделения сигнала с неравномерной шириной каналов (требуемой персептуальной моделью для РС) может быть реализовано на основе полифаз-ной структуры, в которой блоки задержки заменены широкополосными преобразователями (так называемыми "всепропускающими" фильтрами).

Аналитическое описание полифазной структуры СМР приводит к выражению для z -преобразования передаточной функции j -го канала в виде соотношения [1, 2, 4]

M -1

H j ( z ) = Z

P =0

x exp

LJM -1 f

X Г -1"1 PM ⁺ P

Z i(pM+p)’Lz J x

-2 n i •

p =0

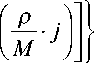
j = 0,1,

M - 1,

где использованы широкополосные характеристики для преобразования РС в каждом канале на основе единого прототипа фильтра h ( k ), k = 0,1, … , L p –1.

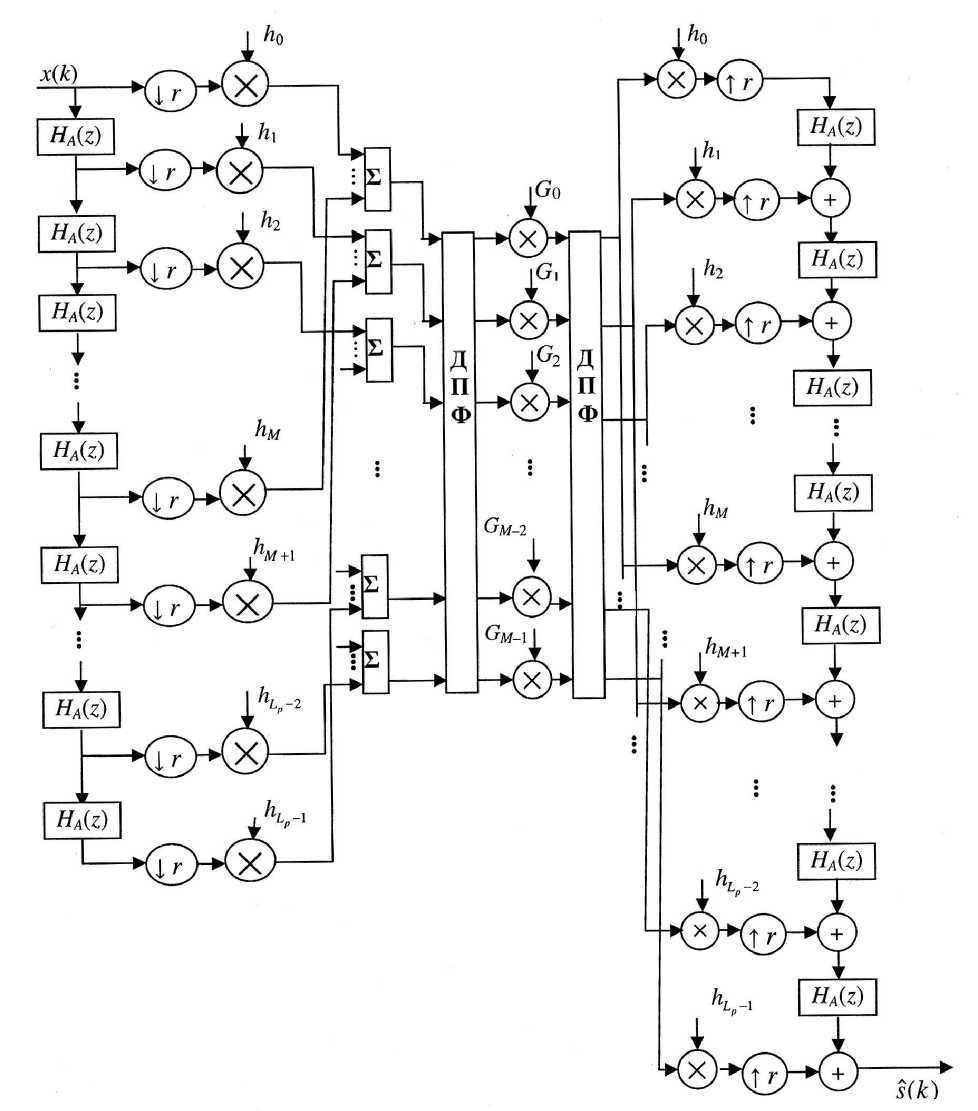
Система СМР на основе модифицированной полифазной структуры с заменой блоков задержки на широкополосные преобразователи показана на рис. 3.

В представленной системе СМР на основе по-лифазной структуры выполнена замена элементов задержки z ^{- 1} на широкополосные преобразователи степени 1, согласно (16):

z-¹ ^ H ( z ) = ^ z^¹ , - 1 <  a < 1. (16) z + a

Это не изменяет величины передаточной функции (ПФ), но вызывает преобразование частоты ω в частотной форме ПФ [14]. Вид преобразования получается из (16) путем подстановки z ^ e *™ . Это дает взаимосвязь первоначальной частоты ω 1 с нелинейно масштабированной частотой ω 2 после преобразования:

to ₂ = 2 arctg

1 + a

1 - a

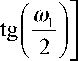
⁶⁾ Шаг временнóго смещения базисной функции при этом меняется по величине в каждой следующей октаве ВП (т. е. при изменении величины параметра m ).

При значениях - 1 <  a <  0 ширина частотных полос фильтров (- широкополосных преобразователей)

Анализ(НФА)        Спектральные веса        Синтез (НФС)

Рис. 3. Система СМР с полифазной структурой и высоким частотным разрешением

возрастает вместе с ростом их центральных частот. При α = 0 получаются одинаковые ширины, а при значениях α из интервала 0<α <1 ширина полос уменьшается по мере увеличения их цен тральных частот.

Аппроксимация спектра РС при масштабировании частоты в барках

Согласно персептуальной модели, основанной на психоакустических экспериментах [5], частотный диапазон РС разделен на интервалы ("критические полосы") с примерно одинаковой относительной шириной — шириной, отнесенной к средней частоте интервала. Критические полосы ведут к концепции нелинейного преобразования шкалы частот. Результатом такого преобразования является частотная шкала η с единицей 1 барк. Масштаб шкалы выбран таким образом, что каждая критическая полоса имеет одинаковую ширину A n = 1 барк . Преобразование диапазона частот РС в эту шкалу может быть аппроксимировано соотношением:

П [ барк ] = 13 • arctg ( 0.76 • f [ кГц ] ) +

+ 3.5 • arctg

f f И

I 7.5 J

С помощью подходящего выбора величины α в соотношении (17) получено приближенное описание каналов СМР, соответствующее виртуальным каналам спектрального преобразования в слуховом аппарате человека. Как отмечено выше, характеристика этих каналов достаточно надежно установлена, отражена в персептуальной модели [5, 6] и выражена частотной шкалой РС в барках. Численное моделирование и анализ системы СМР (рис. 3) показывает, что при значении а = - 0.49 положение и ширина каналов в этой модифицированной СМР на основе полифазной структуры практически идеально соответствует характеристикам анализа человеком звукового спектра РС в диапазоне до 11 кГц.

Отметим, что простая СМР на основе ВП соответствует логарифмическому масштабу преобразования частоты и поэтому дает значительные отклонения (особенно в области низких частот РС) от персептуальной модели.

Восстановление РС в системе СМР

Построение рассмотренных систем СМР для речевого сигнала ориентировано на прагматический критерий — отсутствие заметных на слух искажений на выходе СМР сравнительно с сигналом на входе при условии неиспользования в СМР промежуточного преобразования спектра (в СМР без спектральных весов). Требование полного восстановление РС значительно смягчается в задаче улучшения качества сигнала методом спектрального вычитания фона. Это связано с присущими методу небольшими искажениями сигнала и с появлением незначительного остаточного шума. Обе эти компоненты достаточно хорошо маскируют незначительное искажение РС за счет несовершенного восстановления его в системе СМР. Кроме того, эти небольшие искажения появляются в области высоких частот, а основная часть информационной части РС сосредоточена в пределах 3– 4 кГц. Тесты по прослушиванию РС на выходе СМР подтверждают эти положения.

В связи с этим оказывается возможным строить СМР с прореживанием частоты без использования предельного значения коэффициента снижения эффективной частоты дискретизации (ЭЧД [2]) и тем самым достигать дополнительного снижения элайзинга между каналами. Соотношение коэффициента r снижения ЭЧД при прореживании и величины М повышения частотного разрешения является оптимальным для r = M /4 — это соотношение обеспечивает высокое качество РС на выходе системы СМР.

ЗАКЛЮЧЕНИЕ

Рассмотрены методы улучшения качества речевого сигнала (РС) за счет спектрального вычитания сопутствующего шума. В связи с этой задачей изучены системы согласованного многоканального разделения (СМР), включающие наборы фильтров анализа (НФА) и синтеза (НФС).

• ■    Проанализированы модифицированные структуры систем СМР, построенные по схеме повышенного частотного разрешения. Метод повышенного частного разрешения описан для дискретного вейвлет-преобразования.

• ■    Приведена структура СМР на основе вейв-лет-преобразования, имеющая М -кратно повышенное разрешение по частоте и неравномерную ширину каналов.

• ■    Приведена система СМР с модифицированной полифазной структурой с заменой блоков задержки фильтрами с широкополосным преобразованием РС, с неравномерной шириной каналов и повышенным частотным разрешением.

• ■    Для этой системы СмР показан нелинейный характер изменения частоты при использовании широкополосного преобразователя 1-го порядка и зависимость его от величины параметра α .

• ■    Показан способ эмпирического описания положения и ширины каналов слухового аппарата человека по "персептуальной модели", основанной на экспериментальных данных и реализованной масштабированием частотной шкалы РС в барках.

• ■    Приведено соотношение параметра а и коэффициента М — кратности повышения частотного разрешения (в модифицированной структуре СРМ), которое оптимальным образом соответствует виртуальным каналам частотного анализа РС в слуховом аппарате человека. Для этой структуры

СМР речевого сигнала дана величина параметра α , при которой достигается лучшее преобразование РС по критерию качества восприятия звука.